Как вы думаете почему для контроля передачи файлов используют контрольные суммы а не бит четности

Обновлено: 15.01.2025

Я никогда не использовал контрольную сумму при загрузке различных исполняемых файлов или zip-файлов из Интернета. Я знаю, что он используется для проверки согласованности и повышения безопасности. Но нужно ли это, когда вы скачиваете из солидного проекта вроде Apache или Microsoft. Кто из нас на самом деле использует контрольные суммы или хэш-коды для проверки содержимого?

К вашему сведению, сообщите мне, если я слишком далеко отклонился от приемлемого содержания StackOverflow.

При загрузке файлов, целостность которых критична (например, iso дистрибутива Linux), я на всякий случай склоняю md5 к сумме загрузки.

Источнику можно доверять, но вы никогда не знаете, когда оборудование вашей собственной сетевой карты может начать работать со сбоями.

Другой способ использования - убедиться, что файл, который у вас уже есть, является таким же (т. Е. Неизменным, неповрежденным и текущим), что и файл, доступный для загрузки из надежного источника.

Это может произойти, если

Вы ранее скачали файл
Вы получили файл с другого сайта
Вы получили файл из общего сетевого ресурса
Кто-то дал вам файл на CD / флешке и т. Д.
Вы использовали другой способ избежать потенциально долгой загрузки

Это нужно для того, чтобы вы могли проверить целостность файла. Я использую это все время. По сути, вы просто запускаете какую-то программу, которая будет генерировать контрольную сумму MD5 или какой-либо другой метод хеширования для файла и посмотреть, совпадают ли две контрольные суммы. Если нет, значит файлы разные. Однако обратите внимание, что возможно иметь два файла, которые дают одинаковую контрольную сумму, но вероятность того, что вы столкнетесь с этим, сравнивая два файла одинакового размера, довольно мала, если вы не изобретаете пример.

Это очень полезно. Недавно я обнаружил ошибку в программе записи компакт-дисков; У меня продолжала возникать проблема с определенным файлом на определенном компьютере. Наконец, я просто сравнил контрольные суммы файла с компакт-диска и файла на исходном компьютере, они были разными, и я смог решить проблему!

Имхо, это полезно только в том случае, если вы загрузили большой файл и хотите проверить, не поврежден ли он, прежде чем повторно загружать его (т.е. если приложение не устанавливается правильно).

Чтобы быть уверенным, что загружаемый вами файл является правильным, а не другим, модифицированным другими лицами с злонамеренными намерениями. Как сказано в этой информации в Apache:

" Любой злоумышленник может создать открытый ключ и загрузить его на серверы открытых ключей. Затем он может создать вредоносную версию, подписанную этим поддельным ключом. Затем, если вы попытаетесь проверить подпись этой поврежденной версии, она будет успешной потому что ключ не был «настоящим» ключом. Следовательно, вам необходимо проверить подлинность этого ключа. "

Для проверки вы можете выполнить шаги, указанные здесь.

Он используется для обеих целей целостности (особенно на ftp-сайтах, где вы могли ошибочно загрузить файлы в режиме ascii). Кроме того, его можно использовать для проверки того, что загрузка не была изменена, при условии, что вы загружаете из местоположения a и получаете контрольную сумму из местоположения b (часто загрузка выполняется с зеркала, а хеш - с официального сайта).

Однако в целях обеспечения целостности подписание файла будет более полезным, чем просто его хеширование.

Итак, я должен сказать, что да, я использую контрольные суммы каждый раз, когда устанавливаю программное обеспечение (хотя мой менеджер пакетов делает это автоматически, я не делаю этого напрямую). И даже если вы загружаете вручную из респектабельного проекта, многие захотят загрузить сам код с более быстрого и близкого зеркала, а затем сверить контрольную сумму с копией, загруженной с более надежного главного сервера; Это помогает усложнить атаку, так как придется скомпрометировать несколько серверов, а не только одно зеркало.

выход
в1 Почему для любого канала связи скорость передачи данных ограничена?
Пропускная способность любого канала связи, в котором есть помехи, ограничена. Это значит, что есть некоторая наибольшая возможная скорость передачи данных, которую принципиально невозможно превысить. Зависит от аппаратуры и мощности помех. Не может быть больше скорости света.
назад

теория
в2 В каких случаях при передаче информации допустимы незначительные ошибки?
В реальных каналах связи всегда присутствуют помехи, искажающие сигнал. В некоторых случаях ошибки допустимы, например, при прослушивании радиопередачи через Интернет небольшое искажение звука не мешает понимать речь.
назад

теория
В4 в каких случаях с помощью бита четности можно обнаружить ошибку, а в каких – нельзя?
Бит чётности позволяет обнаруживать нечётное число ошибок (1, 3, 5, . ), а ошибки в чётном количестве разрядов остаются незамеченными. Контроль применяется для небольших блоков данных (чаще всего — для каждого отдельного байта) и хорошо работает тогда, когда отдельные ошибки при передаче независимы одна от другой и встречаются редко.
назад

теория
В6 как вы думаете, почему для контроля передачи файлов используются контрольные суммы, а не бит четности?
Используя бит четности, легко и быстро работать, но если произошло более одной ошибки, то ее можно не заметить. Используя контрольные суммы каждая ошибка будет обнаружена, но при передаче и получении нужно будет вычислять эту контрольную сумму, что приведет к временным затратам.
назад

теория
В8 как исправляется ошибка при использовании помехоустойчивого кода?
Для исправления ошибки нужно к символу разряда в котором произошла ошибка прибавить единицу по модулю два.

теория
В9 какие достоинства и недостатки есть у кодов хэмминга с большим размером блоков?
Недостаток кода Хэмминга — некратность размера исходного блока кода и блока кода степени двойки. Это затрудняет обработку кодов Хэмминга на компьютерах, оперирующих блоками бит кратными степени двойки. Достоинство в том, что реализация алгоритма требует небольших ресурсов и может быть выполнена аппаратно. Исходными данными для кодирования является произвольная двоичная последовательность.

При передачи данных по линиям связи, используется контрольная сумма, рассчитанная по некоторому алгоритму. Алгоритм часто сложный, конечно, он обоснован математически, но очень уж неудобен при дефиците ресурсов, например при программировании микроконтроллеров.

Чтобы упростить алгоритм, без потери качества, нужно немного «битовой магии», что интересная тема сама по себе.

Без контрольной суммы, передавать данные опасно, так как помехи присутствуют везде и всегда, весь вопрос только в их вероятности возникновения и вызываемых ими побочных эффектах. В зависимости от условий и выбирается алгоритм выявления ошибок и количество данных в контрольной сумме. Сложнее алгоритм, и больше контрольная сумма, меньше не распознанных ошибок.

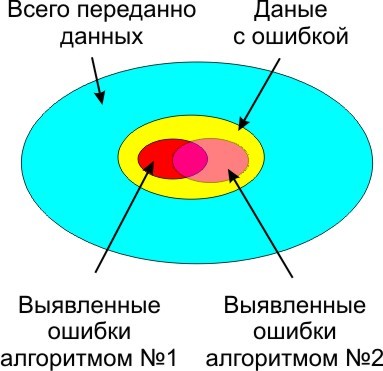
Причина помех на физическом уровне, при передаче данных.

Вот пример самого типичного алгоритма для микроконтроллера, ставшего, фактически, промышленным стандартом с 1979 года.

Не слабый такой код, есть вариант без таблицы, но более медленный (необходима побитовая обработка данных), в любом случае способный вынести мозг как программисту, так и микроконтроллеру. Не во всякий микроконтроллер алгоритм с таблицей влезет вообще.

Давайте разберем алгоритмы, которые вообще могут подтвердить целостность данных невысокой ценой.

Бит четности (1-битная контрольная сумма)

На первом месте простой бит четности. При необходимости формируется аппаратно, принцип простейший, и подробно расписан в википедии. Недостаток только один, пропускает двойные ошибки (и вообще четное число ошибок), когда четность всех бит не меняется. Можно использовать для сбора статистики о наличии ошибок в потоке передаваемых данных, но целостность данных не гарантирует, хотя и снижает вероятность пропущенной ошибки на 50% (зависит, конечно, от типа помех на линии, в данном случае подразумевается что число четных и нечетных сбоев равновероятно).
Для включения бита четности, часто и код никакой не нужен, просто указываем что UART должен задействовать бит четности. Типично, просто указываем:

Часто разработчики забывают даже, что UART имеет на борту возможность проверки бита четности. Кроме целостности передаваемых данных, это позволяет избежать устойчивого срыва синхронизации (например при передаче данных по радиоканалу), когда полезные данные могу случайно имитировать старт и стоп биты, а вместо данных на выходе буфера старт и стоп биты в случайном порядке.

Если контроля четности мало (а этого обычно мало), добавляется дополнительная контрольная сумма. Рассчитать контрольную сумму, можно как сумму ранее переданных байт, просто и логично

Естественно биты переполнения не учитываем, результат укладываем в выделенные под контрольную сумму 8 бит. Можно пропустить ошибку, если при случайном сбое один байт увеличится на некоторое значение, а другой байт уменьшится на то же значение. Контрольная сумма не изменится. Проведем эксперимент по передаче данных. Исходные данные такие:

Блок данных 8 байт.
Заполненность псевдослучайными данными Random($FF+1)
Случайным образом меняем 1 бит в блоке данных операцией XOR со специально подготовленным байтом, у которого один единичный бит на случайной позиции.
Повторяем предыдущий пункт 10 раз, при этом может получится от 0 до 10 сбойных бит (2 ошибки могут накладываться друг на друга восстанавливая данные), вариант с 0 сбойных бит игнорируем в дальнейшем как бесполезный для нас.

на 256 отправленных телеграмм с ошибкой, одна пройдет проверку контрольной суммы. Смотрим статистику от виртуальной передачи данных, с помощью простой тестовой программы:

1: 144 (тут и далее — вероятность прохождения ошибки)
1: 143
1: 144
1: 145
1: 144
1: 142
1: 143
1: 143
1: 142
1: 140
Общее число ошибок 69892 из 10 млн. итераций, или 1: 143.078

Не смотря на вероятность прохождения ошибки 1:143, вероятность обнаружения ошибки лучше, чем 1:256 невозможна теоретически. Потери в качестве работы есть, но не всегда это существенно. Если нужна надежность выше, нужно использовать контрольную сумму с большим числом бит. Или, иначе говоря, простая контрольная сумма, недостаточно эффективно использует примерно 0.75 бита из 8 имеющихся бит информации в контрольной сумме.

Для сравнения применим, вместо суммы, побитовое сложение XOR. Стало существенно хуже, вероятность обнаружения ошибки 1:67 или 26% от теоретического предела. Упрощенно, это можно объяснить тем, что XOR меняет при возникновении ошибке еще меньше бит в контрольной сумме, ниже отклик на единичный битовый сбой, и повторной ошибке более вероятно вернуть контрольную сумму в исходное состояние.

Так же можно утверждать, что контрольная сумма по XOR представляет из себя 8 независимых контрольных сумм из 1 бита. Вероятность того, что ошибка придется на один из 8 бит равна 1:8, вероятность двойного сбоя 1:64, что мы и наблюдаем, теоретическая величина совпала с экспериментальными данными.

Нам же нужен такой алгоритм, чтобы заменял при единичной ошибке максимальное количество бит в контрольной сумме. Но мы, в общей сложности, ограниченны сложностью алгоритма, и ресурсами в нашем распоряжении. Не во всех микроконтроллерах есть аппаратный блок расчета CRC. Но, практически везде, есть блок умножения. Рассчитаем контрольную сумму как произведение последовательности байт, на некоторую «магическую» константу:

Константа должна быть простой, и быть достаточно большой, для изменения большего числа бит после каждой операции, 211 вполне подходит, проверяем:

1: 185
1: 186
1: 185
1: 185
1: 193
1: 188
1: 187
1: 194
1: 190
1: 200

Всего 72% от теоретического предела, небольшое улучшение перед простой суммой. Алгоритм в таком виде не имеет смысла. В данном случае теряется важная информация из отбрасываемых старших 8..16 бит, а их необходимо учитывать. Проще всего, смешать функцией XOR с младшими битами 1..8. Приходим к еще более интенсивной модификации контрольной суммы, желательно с минимальным затратами ресурсов. Добавляем фокус из криптографических алгоритмов

1: 237
1: 234
1: 241
1: 234
1: 227
1: 238
1: 235
1: 233
1: 231
1: 236

Результат 91% от теоретического предела. Вполне годится для применения.

Если в микроконтроллере нет блока умножения, можно имитировать умножение операций сложения, смещения и XOR. Суть процесса такая же, модифицированный ошибкой бит, равномерно «распределяется» по остальным битам контрольной суммы.

1: 255
1: 257
1: 255
1: 255
1: 254
1: 255
1: 250
1: 254
1: 256
1: 254

На удивление хороший результат. Среднее значение 254,5 или 99% от теоретического предела, операций немного больше, но все они простые и не используется умножение.

1: 260
1: 250
1: 252
1: 258
1: 261
1: 255
1: 254
1: 261
1: 264
1: 262

Что соответствует 100.6% от теоретического предела, вполне хороший результат для такого простого алгоритма из одной строчки:

Используется полноценное 16-битное умножение. Опять же не обошлось без магического числа 44111 (выбрано из общих соображений без перебора всего подмножества чисел). Более точно, константу имеет смысл подбирать, только определившись с предполагаемым типом ошибок в линии передачи данных.

Столь высокий результат объясняется тем, что 2 цикла умножения подряд, полностью перемешивают биты, что нам и требовалось. Исключением, похоже, является последний байт телеграммы, особенно его старшие биты, они не полностью замешиваются в контрольную сумму, но и вероятность того, что ошибка придется на них невелика, примерно 4%. Эта особенность практически ни как не проявляется статистически, по крайней мере на моем наборе тестовых данных и ошибке ограниченной 10 сбойными битами. Для исключения этой особенности можно делать N+1 итераций, добавив виртуальный байт в дополнение к имеющимся в тестовом блоке данных (но это усложнение алгоритма).

Результат 100.6% от теоретического предела.

Вариант без умножения более простой, оставлен самый минимум функций, всего 3 математических операции:

Результат 86% от теоретического предела.

В этом случае потери старших бит нет, они возвращаются в младшую часть переменной через функцию XOR (битовый миксер).

Небольшое улучшение в некоторых случаях дает так же:

Двойной проход по обрабатываемым данным. Но ценой усложнения алгоритма (внешний цикл нужно указать), ценой удвоения времени обработки данных.
Обработка дополнительного, виртуального байта в конце обрабатываемых данных, усложнения алгоритма и времени работы алгоритма практически нет.
Использование переменной для хранения контрольной суммы большей по разрядности, чем итоговая контрольная сумма и перемешивание младших бит со старшими.

16-битная контрольная сумма

Далее, предположим что нам мало 8 бит для формирования контрольной суммы.

Следующий вариант 16 бит, и теоретическая вероятность ошибки переданных данных 1:65536, что намного лучше. Надежность растет по экспоненте. Но, как побочный эффект, растет количество вспомогательных данных, на примере нашей телеграммы, к 8 байтам полезной информации добавляется 2 байта контрольной суммы.

Модифицируем алгоритм для обработки контрольной суммы разрядностью 16 бит, надо отметить, что тут так же есть магическое число 8 и 44111, значительное и необоснованное их изменение ухудшает работу алгоритма в разы.

1: 43478
1: 76923
1: 83333
1: 50000
1: 83333
1: 100000
1: 90909
1: 47619
1: 50000
1: 90909

Что соответствует 109% от теоретического предела. Присутствует ошибка измерений, но это простительно для 10 млн. итераций. Так же сказывается алгоритм создания, и вообще тип ошибок. Для более точного анализа, в любом случае нужно подстраивать условия под ошибки в конкретной линии передачи данных.

Дополнительно отмечу, что можно использовать 32-битные промежуточные переменные для накопления результата, а итоговую контрольную сумму использовать как младшие 16 бит. Во многих случаях, при любой разрядности контрольной суммы, так несколько улучшается качество работы алгоритма.

32-битная контрольная сумма

Перейдем к варианту 32-битной контрольной суммы. Появляется проблема со временем отводимым для анализа статистических данных, так как число переданных телеграмм уже сравнимо с 2^32. Алгоритм такой же, магические числа меняются в сторону увеличения

За 10 млн. итераций ошибка не обнаружена. Чтобы ускорить сбор статистики обрезал CRC до 24 бит:

Результат, из 10 млн. итераций ошибка обнаружена 3 раза

1: 1000000
1: no
1: no
1: no
1: 1000000
1: no
1: 1000000
1: no
1: no
1: no

Вполне хороший результат и в целом близок к теоретическому пределу для 24 бит контрольной суммы (1:16777216). Тут надо отметить что функция контроля целостности данных равномерно распределена по всем битам CRC, и вполне возможно их отбрасывание с любой стороны, если есть ограничение на размер передаваемой CRC.

Для полноценных 32 бит, достаточно долго ждать результата, ошибок просто нет, за приемлемое время ожидания.

Вариант без умножения:

Сбоя для полноценной контрольной суммы дождаться не получилось. Контрольная сумма урезанная до 24 бит показывает примерно такие же результаты, 8 ошибок на 100 млн. итераций. Промежуточная переменная CRC 64-битная.

64-битная контрольная сумма

Ну и напоследок 64-битная контрольная сумма, максимальная контрольная сумма, которая имеет смысл при передачи данных на нижнем уровне:

Дождаться ошибки передачи данных, до конца существования вселенной, наверное не получится :)

Метод аналогичный тому, какой применили для CRC32 показал аналогичные результаты. Больше бит оставляем, выше надежность в полном соответствии с теоретическим пределом. Проверял на младших 20 и 24 битах, этого кажется вполне достаточным, для оценки качества работы алгоритма.

Рекомендую к использованию в микроконтроллерах, или для проверки целостности любых переданных данных. Вполне рабочий метод, уже как есть, не смотря на простоту алгоритма.

Мой проект по исследованию CRC на гитхаб.

Далее интересно было бы оптимизировать алгоритм на более реальных данных (не псевдослучайные числа по стандартному алгоритму), подобрать более подходящие магические числа под ряд задач и начальных условий, думаю можно еще выиграть доли процента по качеству работы алгоритма. Оптимизировать алгоритм по скорости, читаемости кода (простоте алгоритма), качеству работы. В идеале получить и протестировать образцы кода для всех типов микроконтроллеров, для этого как-раз и нужны примеры с использованием умножения 8, 16, 32 битных данных, и без умножения вообще.

Контрольная сумма - это небольшой блок данных, полученный из другого блока цифровых данных с целью обнаружения ошибок, которые могли быть внесены во время его передачи или хранения . Сами по себе контрольные суммы часто используются для проверки целостности данных, но не используются для проверки подлинности данных .

Процедура , которая формирует эту контрольную сумму, называется функцией контрольной суммы или контрольная сумма алгоритм . В зависимости от целей разработки хороший алгоритм контрольной суммы обычно выводит существенно другое значение, даже при небольших изменениях, внесенных во входные данные. Это особенно верно для криптографических хэш-функций , которые могут использоваться для обнаружения многих ошибок повреждения данных и проверки общей целостности данных ; если вычисленная контрольная сумма для текущего ввода данных совпадает с сохраненным значением ранее вычисленной контрольной суммы, существует очень высокая вероятность того, что данные не были случайно изменены или повреждены.

Функции контрольной суммы связаны с хэш-функциями , отпечатками пальцев , функциями рандомизации и криптографическими хеш-функциями . Однако у каждой из этих концепций разные приложения и, следовательно, разные цели проектирования. Например, функция, возвращающая начало строки, может предоставить хэш, подходящий для некоторых приложений, но никогда не будет подходящей контрольной суммой. Контрольные суммы используются в качестве криптографических примитивов в более крупных алгоритмах аутентификации. Для криптографических систем с этими двумя конкретными целями проектирования см. HMAC .

Контрольные цифры и биты четности являются частными случаями контрольных сумм, ассигновать для небольших блоков данных (например, номера социального страхования , банковские счета чисел, машинных слов , отдельных байтов и т.д.). Некоторые коды с исправлением ошибок основаны на специальных контрольных суммах, которые не только обнаруживают общие ошибки, но также позволяют в определенных случаях восстанавливать исходные данные.

Содержание

Простые контрольные суммы, описанные выше, не позволяют обнаружить некоторые общие ошибки, которые затрагивают сразу несколько битов, такие как изменение порядка слов данных или вставка или удаление слов со всеми битами, установленными в ноль. Алгоритмы контрольной суммы, наиболее часто используемые на практике, такие как контрольная сумма Флетчера , Adler-32 и циклический контроль избыточности (CRC), устраняют эти слабые места, учитывая не только значение каждого слова, но и его позицию в последовательности. Эта функция обычно увеличивает стоимость вычисления контрольной суммы.

Идея нечеткой контрольной суммы была разработана для обнаружения спама в электронной почте путем создания совместных баз данных от нескольких интернет-провайдеров электронной почты, подозреваемой в спаме. Содержание такого спама часто может отличаться по деталям, что делает обычное вычисление контрольной суммы неэффективным. Напротив, «нечеткая контрольная сумма» сокращает основной текст до характерного минимума, а затем генерирует контрольную сумму обычным образом. Это значительно увеличивает вероятность того, что несколько различающиеся спам-письма будут давать одинаковую контрольную сумму. Программное обеспечение для обнаружения спама интернет-провайдеров, такое как SpamAssassin , сотрудничающих интернет-провайдеров отправляет контрольные суммы всех электронных писем в централизованную службу, такую как DCC.. Если количество отправленных нечетких контрольных сумм превышает определенный порог, база данных отмечает, что это, вероятно, указывает на спам. Пользователи услуг ISP аналогичным образом генерируют нечеткую контрольную сумму для каждого из своих электронных писем и запрашивают услугу на предмет вероятности спама. [2]

Читайте также: