Как транспортиром сделать угол 60 градусов

© Depositphotos
Сколько градусов в угле
Общепринятой единицей измерения плоских углов является градус. Почему математики древности выбрали именно такую единицу и почему в окружности 360 градусов, а не, скажем, 1000, точно неизвестно.
Одна из гипотез усматривает тут связь с тем, что в году приблизительно 360 дней. Другая гласит, что шумеры выбрали число 360, основываясь на своей шестидесятеричной системе счисления.
Так или иначе, а углы присутствуют не только на страницах учебников, но и повсеместно окружают нас в реальной жизни. Прямой угол легко найти в очертаниях зданий, изгибах мебели и каждом печатном листе.

Без угла в 45 градусов ни один столяр не смастерит простейшую рамку. Угол в 60 градусов требуется для построения равносторонних треугольников. Угол 30 градусов используется редко, но помогает получить угол в 120 градусов, необходимый для построения правильного шестиугольника.
Измеряем угол без транспортира
При наличии транспортира всё просто. Размести его центр в вершине угла, а основание совмести с одной из сторон. Проследи за второй стороной угла. В том месте, где она пересечет дугу транспортира, и будет указана величина угла в градусах.

Без транспортира под рукой, как обычно и бывает, задача усложняется. Но смекалка выручит нас и здесь. Вытяни руку ладонью вверх и максимально расставь пальцы.
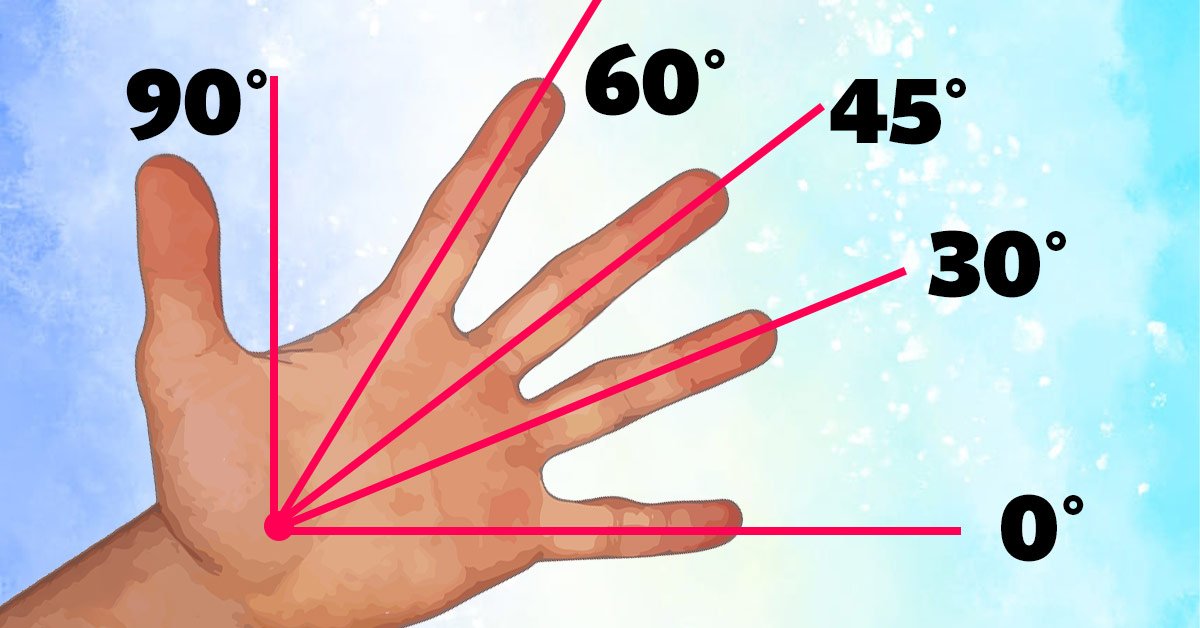
Следи за тем, чтобы большой палец находился перпендикулярно мизинцу. Тогда, если мизинец указывает на 0 градусов, то безымянный будет указывать на 30, средний на 45, указательный на 60, а большой на 90 градусов.

© Depositphotos
Способ, конечно, не очень точный, но всегда поможет приблизительно понять, с каким углом ты имеешь дело. Раньше мы рассказывали о полезном для каждого домашнего мастера угле в 22,5 градуса, который позволяет правильно заточить ножи. Выдержать его поможет сложенный вчетверо лист бумаги.
Строим углы в 90, 60 и 30 градусов без транспортира
Если нужен угол в 30, 60, 90 градусов, а транспортира или шаблона под рукой нет, помогут эти простые способы. Чтобы получить точный угол в 90 градусов, построй Пифагоров треугольник со сторонами, кратными 3,4,5.

Для этого, например, начерти отрезок длиной 5 см и проведи из его концов дуги с радиусами 3 и 4 см. Теперь соедини точку их пересечения с концами отрезка. Получится прямоугольный треугольник и угол, расположенный напротив гипотенузы, будет составлять ровно 90 градусов.
Когда уже есть прямой угол, легко получить углы в 30 и 60 градусов поможет магическое число 173 (его хорошо бы запомнить). Отложи по одной стороне прямого угла отрезок в 100 мм, а по другой — 173. Соедини их концы. Ты получишь шаблон с углами 90, 60 и 30 градусов!
Математикой должны заниматься блондинки - они врать не умеют.
воскресенье, 20 октября 2013 г.
Простое построение углов
Тут мне в комментариях задали интересный вопрос. Простое построение углов - как это сделать? Вот сам вопрос.
 |
| Вопрос о построении углов |
И так, вопрос сводится к следующему - в декартовой системе координат, если брать одинаковый икс и игрек, получим прямую под углом в 45 градусов к осям координат. А как построить углы другой величины? Можно, конечно, заняться гаданием на кофейной гуще и попробовать высчитать, сколько нужно откладывать по иксам, сколько по игрекам, чтобы получился другой удобочитаемый угол. Не 156пи/911, а что-то типа 1, 5, 10, 15 градусов.
Угол в тридцать градусов получается, когда по оси игрек мы возьмем половинку, а расстояние от центра системы координат до точки будет равно единице. При помощи циркуля и линейки такое построить можно, но.
 |
| Построение угла в 30 градусов |
И так, четвертое-пятое тысячелетие до нашей эры, древняя Месопотамия. Тогда зародилось то, чем мы пользуемся и сегодня. Астрономия, письменность, математика, углы. Какими инструментами тогда пользовались для построения углов? Линейка, циркуль. Возможно, были тогда и угольники, хотя это не принципиально - для построения прямого угла достаточно циркуля и линейки.
Теперь попробуем строить углы при помощи циркуля и линейки без всяких координатных систем. Проводим прямую линию, строим окружность с центром на построенной линии. Ставим циркуль в точки пересечения линии и окружности и строим две окружности того же радиуса. Соединяем линиями центр первой окружности точки пересечения окружностей. У нас получились углы в 60 градусов.
 |
| Построение угла в 60 градусов |
Почему возле углов я поставил циферки 1, 2, 3, 4, 5, 6? Я считаю, что именно такую единицу измерения углов использовали наши предки. Назовем эту единицу измерения углов "вавилонский угол". Дальше один угол делится на 60 градусов. Почему именно на 60? В те времена, в тех местах, использовалась шестидесятеричная система счисления. Вы такой системой счисления никогда не пользовались и понятия о ней не имеете? Ошибаетесь. Когда вы выражаете время в минутах и секундах, вы используете именно шестидесятеричное счисление. "Подожди пять минут" в переводе на десятичные дроби, если за единицу брать один час, будет звучать как "Подожди 0,083333333. часа". Дико звучит, не правда ли?
Давайте посмотрим на структуру вавилонских шестидесятеричных чисел. Единицу целого числа вавилоняне делили на шестьдесят частей. Потом каждую эту часть делили ещё на шестьдесят частей и так дальше. У шестидесятых долей были свои названия: минута, секунда, терция.
 |
| Минута, секунда, терция, кварта, квинта |
Я просто хотел обратить ваше внимание на то, что 360 градусов окружности приблизительно равны 365 дням в году (если отбросить градусы и дни, а тупо сравнивать только числа, как это любят делать наши математики). Почему я сравниваю окружность с днями в году? За сутки Солнце смещается по эклиптике приблизительно на один градус. С другой стороны, вавилонский угол в 60 градусов приблизительно равен одному радиану. Ведь 1 радиан ≈ 57,295779513° ≈ 57° 17′ 44,806″ При этом, у вавилонского угла есть точное числовое значение, а вот радиан точного числового значения не имеет - он построен на бесконечности числа "пи". Один - ноль в пользу древних математиков. Что бы там не утверждали наши математики, но принимать в качестве единицы измерения бесконечное число - это не совсем разумно. Думаю, физики меня поймут - создать точный измерительный прибор для измерения неточной величины даже теоретически невозможно.
Но продолжим наши построения углов. Через центр первой окружности проводим перпендикуляр, затем строим ещё две окружности с центрами в точках пересечения перпендикуляра и первой окружности.
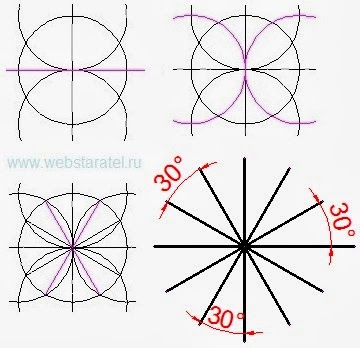 |
| Построение угла в 30 градусов |
 |
| Вавилонские углы и циферблат часов |
Особо стоит отметить, что в древности использовались солнечные часы. Было два варианта солнечных часов - напольные и настенные. Так вот, стрелки этих двух типов часов (тень на циферблате) двигались в противоположных направлениях - по часовой стрелке у напольных и против часовой стрелки у настенных. Можно предположить, что такого понятия, как "вращение по часовой стрелке" у древних математиков не существовало. А в том, что древние люди были очень умными, мы можем убедиться, рассмотрев загадку вавилонской таблички.

В этом уроке мы узнаем историю возникновения транспортира. Введем понятие градус. Определим алгоритм построения углов при помощи транспортира, алгоритм измерения углов при помощи транспортира. Сформируем представления о остром угле, тупом угле

В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Измерение углов. Транспортир"
На этом уроке мы познакомимся с прибором для измерения углов – транспортиром. Научимся с помощью транспортира измерять и строить углы.
Коснёмся истории, чтобы узнать, как появился транспортир.
Древние вавилонские математики и астрономы полный оборот (окружность) разделили на столько частей, сколько дней в году. Они думали, что в году 360 дней. Поэтому круг, обозначающий год, они разделили на 360 равных частей. Такое изображение было очень удобным. На нём можно было отмечать каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой части дали название – градус. Каждый градус разделили на 60 минут, а минуту – на 60 секунд. Градусная мера сохранилась и до наших дней.
Итак, для измерения углов применяют транспортир.

Транспортир состоит из линейки (прямолинейной шкалы) и полуокружности (угломерной шкалы). Центр этой полуокружности отмечен на транспортире или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
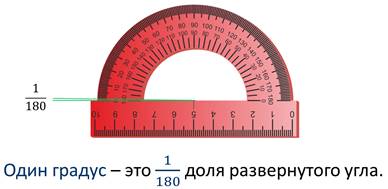
Если из центра этой полуокружности провести лучи через каждый штрих, то получится 180 углов. Каждый, из которых равен доле развернутого угла.
Определение
Такие углы принято называть градусами.
Градусы обозначают вот таким знаком °.
Каждое деление шкалы транспортира равно 1°. Кроме делений по 1° на шкале транспортира есть ещё деления по 5° и по 10°.
А теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм измерения углов:
1) Совместить вершину угла с центром транспортира.
2) Расположить транспортир так, чтобы одна из сторон угла проходила через начало отсчёта на шкале транспортира; 0 – начало отсчёта.
3) Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте, используем ту шкалу для определения градусной меры угла, где располагается нулевой градус).
4) Смотрим, через какой штрих проходит вторая сторона и какой градус соответствует этому штриху.
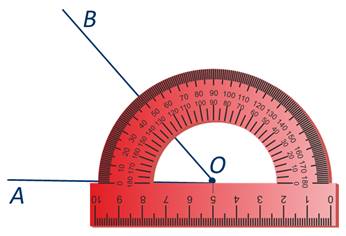
На нашем слайде угол АОВ равен 50°. Пишут так:
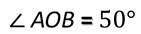
Развёрнутый угол равен 180°. Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла, то он равен
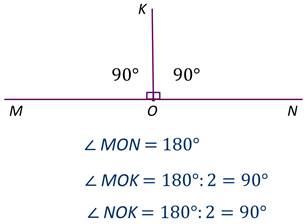
Прямой угол равен 90°.
Так как равные углы полностью совмещаются при наложении, то равные углы имеют равные градусные меры. Следовательно, больший угол имеет большую градусную меру, меньший угол имеет меньшую градусную меру.
Транспортир применяют и не только для измерения углов, а также и для их построения.
Запомним алгоритм построения углов.
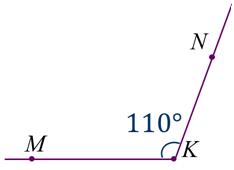
Алгоритм будем исследовать на конкретном примере: построить угол МКN равный 110°.
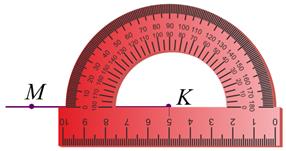
1. Отметим произвольную точку и обозначим её буквой К.
2. Начертим луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.

3. Наложим транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через начало отсчёта на шкале.
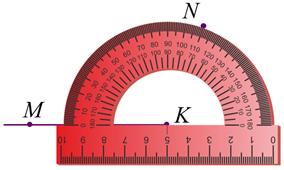
4. На этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на чертеже точку N против штриха с отметкой 110°.
5. Проведём луч КN. Построенный нами угол МКN и есть искомый.
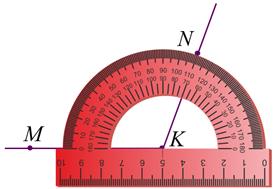
6. Не забудем записать МКN = 110°.
Такой же угол можно построить и по другую сторону от луча КМ.
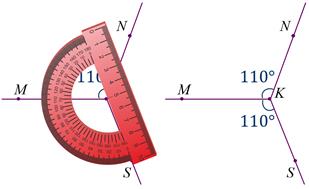
Повсюду есть углы любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.
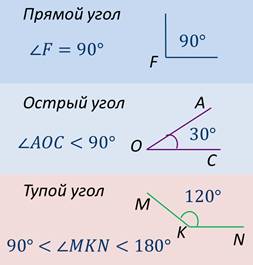
Определение
Если угол меньше 90°, то его называют острым углом.
Если угол больше 90°, но меньше 180°, то его называют тупым углом.
На экране изображены угол АОС – острый и угол МКN – тупой. Градусная мера угла АОС равна 30°, т.е. меньше 90°, следовательно, он острый. Градусная мера угла МКN равна 120°, т.е. больше 90°, но меньше 180°, следовательно, он тупой.
Итак, сегодня на уроке мы познакомились с прибором для измерения углов – транспортиром. Научились с помощью него измерять и строить углы.
Транспортир — это математический инструмент, состоящий из линейки и полукруга, разделённого на градусы от 0 до 180°. Он применяется для измерения и построения углов в рисовании и математическом черчении, наряду с составлением графиков в физике. Научиться пользоваться транспортиром достаточно просто.

Люди обычно сталкиваются с транспортирами в математике, когда учатся в школе создавать точные геометрические фигуры. Возможно, у многих из них никогда больше не будет причин снова использовать эти приборы, тем не менее транспортиры имеют долгую историю применения в различных областях.
История изобретения
Происхождение этого математического инструмента восходит к жрецам в Египте и Вавилоне, которые установили меру углов в градусах, минутах и секундах. Однако до времён классической Греции тригонометрия не использовалась в математике.
Птолемей также был автором, так называемой теоремы Менелая для решения сферических треугольников, и на протяжении многих веков его тригонометрия была основным пособием для астрономов.

Возможно, в то же время, учёные Индии также разработали тригонометрическую систему, основанную на функции синуса, которая, в отличие от используемого в настоящее время синуса, была не пропорцией, а длиной стороны, противоположной углу в прямом треугольнике этой гипотенузы. Индийские математики использовали разные значения для этого в своих таблицах.
Другие европейские математики также описывали подобные приборы примерно в то же время. Независимо от того, кто первым придумал этот инструмент, к началу XVII века он вошёл в стандартную практику мореплавателей и геодезистов. К XVIII веку транспортиры начали появляться в учебниках по геодезии и геометрии.
Транспортиры в современном понимании возникли во второй половине XVIII века, когда такие учёные, как Джесси Рамсден и Георг Фридрих Брандер, усовершенствовали ранее созданные устройства.
В то время предпочтительными материалами для их изготовления были:

- дерево;
- латунь;
- серебро;
- медь;
- слоновая кость.
В первой половине XX века начали применять олово и целлулоид.
Разновидности и использование
Транспортир — это простой гониометр для измерения или создания угла. Он выглядит как круглый или полукруглый диск с делением. Диск может быть изготовлен из пластика, прочной бумаги или листового металла. Типичными являются диаметры от 8 до 15 см и деления на 1° и 0,5°, при измерении также 0,5 Гон (новый градус). Точность составляет от 0,1 до 0,5° в зависимости от диаметра шкалы. Более точные приборы имеют поворотную рейку со шкалой (длина до миллиметра).

Частично из-за различного использования их изготавливают во многих формах: знакомый полукруг, а также круги, прямоугольники, квадраты или четверть круга (квадранты). Они также могут иметь различные диаметры. Их изготавливают из латуни, стали, дерева, слоновой кости или пластика. Самой распространённой формой является полукруг с ограничительной шкалой в 180 градусов.
Угловой транспортир — градуированный круглый инструмент с одной поворотной рукой; используется для измерения или разметки. В строительстве часто требуется отмерить угол в 90 градусов. Иногда прилагается шкала Вернье, чтобы дать более точные показания. Прибор широко применяется для изготовления архитектурных и механических чертежей, хотя его использование уменьшилось с появлением современного программного обеспечения для рисования.
Универсальные транспортиры скоса используются изготовителями инструментов; поскольку они делают измерения посредством механического контакта с предметом, то классифицируются как механические транспортиры.
Угловой транспортир применяется для того, чтобы измерить и проверить углы с очень жёсткими допусками. Он считывает до 5 угловых минут (5 или 1/12°) и может измерять от 0 до 360°.
Сегодня также применяются электронные приборы, которые обычно работают с поворотным датчиком. Кроме того, связанными с транспортиром приборами являются:
- теодолит;
- оптический транспортир в строительной промышленности и геодезии;
- инклинометр для определения уклонов и косвенной альтиметрии;
- секстант для навигации.
Измерение градусов угла
Для того чтобы научиться пользоваться транспортиром инструкция нужна на начальном этапе. Для его освоения достаточно нескольких минут и примеров (смотреть онлайн) того, как можно измерить и построить угол с помощью этого прибора.
Измерить угол, значит найти его величину. Углы разделяют на три типа: острый, тупой и прямой. Прямоугольный имеет 90 градусов. Все углы что имеют больше этого значения называются тупыми, и соответственно меньше 90 градусов называются острыми. Развёрнутый угол имеет 180 градусов.

Понимание того, что углы являются частями окружностей, полезно, потому что тогда конструкция транспортира обретает смысл. Поскольку полный круг имеет 360º, отдельный угол должен быть меньше этого числа, потому что он часть круга.
Алгоритм измерения следующий: для того чтобы измерить угол транспортиром необходимо приложить его центр верхней кромки линейки к вершине измеряемого угла. Вершина — это точка, в которой две из трёх сторон треугольника пересекаются.
Нижнюю планку (основание) транспортира нужно выставить горизонтально. Каждый транспортир имеет точку, спроектированную в центре основания, Эта средняя точка располагается на вершине угла, который должен быть измерен или нанесён на график. Другая сторона должна пересекать транспортир в одной из точек его дуги.
Если вторая сторона (линия) до дуги не доходит нужно продолжить её с помощью простой или масштабной линейки. То число, на шкале дуги, которое будет пересечено линией и есть величина угла в градусах.
Для удобства на большинстве транспортиров сделано две шкалы, внутренняя и внешняя, которые отображают числа в каждой строке.
Построение угла
Берётся чистый лист бумаги в клетку. На нём карандашом отмечается точка, от которой проводиться прямая линия, как одна из сторон будущего угла. Эта черта служит для того, чтобы задать направление второй стороне. В простых упражнениях, для приобретения навыка построения угла, линия проводится горизонтально.

Центр основы транспортира располагается на любом из концов черты, который будет вершиной угла. Эта точка отмечается на бумаге карандашом. И именно к этому месту, внутри отверстия и присоединяется вершина угла, одна из сторон которого должна совпадать в горизонтальной плоскости с внутренней стороной линейки транспортира.
Затем на шкале отмечается необходимый градус. С внутренней стороны отверстия также обозначается точка возле этого градуса. И от вершины проводится прямая линия к этой точке. Таким образом, получается необходимый угол.
Для того чтобы правильно пользоваться транспортиром очень важно его выровнять, и точно прикладывать, для получения верных измерений.
Пересечённые линии в верхней части прямой кромки линейки должны совпадать с вершиной (конечной точкой), где соединяются два луча.
Читайте также:


