Как сделать функцию с двумя переменными
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.
§43. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
43.1. Основные понятия
Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, называется функцией двух переменных, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ : D → R При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).
Множество D = D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается E(f) или Е.
Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество 0, у > 0>.
Функцию z = ƒ(х;у), где (х;у) є D можно понимать (рассматривать) как функцию точки М(х;у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью.
Значение функции z = ƒ(х;у) в точке М0(х0;у0) обозначают z0=ƒ(хо;уо) или z0=ƒ(М0) и называют частным значением функции.
Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке М0(х0; у0) области D в системе координат Oxyz соответствует точка M(x0;y0;z0), где z0 = ƒ(хо;уо) — аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z=ƒ(x;у).
Например, функцияимеет областью определения круг х 2 + у 2 ≤ 1 и изображается верхней полусферой с центром в точке O(0;0;0) и радиусом R = 1 (см. рис. 205).
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.
43.2. Предел функции
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х;у) плоскости, координаты которых удовлетворяют неравенствуназывается d -окрестностью точки М0(х0;у0). Другими словами, d -окрестность точки Мо — это все внутренние точки круга с центром Мо и радиусом 8 (см. рис. 206).
Пусть функция z = ƒ(х; у) определена в некоторой окрестности точки М0(х0;у0), кроме, быть может, самой этой точки. Число А называется пределом функции z = ƒ (х; у) при х → х0 и у → у0 (или, что то же самое, при М(х; у) → М0(х0; у0)), если для любого є > 0 существует d > 0 такое, что для всех х ≠ х0 и у ≠ у0 и удовлетворяющих неравенству
выполняется неравенство | ƒ (х; у) — А| → х0 по двум направлениям: справа и слева!)
Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число є>0, найдется d -окрестность точки Mо(хо;уо), что во всех ее точках М(х;у), отличных от Мо, аппликаты соответствующих точек поверхности z=ƒ(х;у) отличаются от числа А по модулю меньше, чем на є.
Пример 43.1. Найти предел
Решение: Будем приближаться к О(0;0) по прямой у=Кх, где К — некоторое число. Тогда
Функция в точке О(0; 0) предела не имеет, т. к. при разных значенияхК предел функции не одинаков (функция имеет различные предельные значения).
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной (см. п. 17.3). Это означает, что справедливы утверждения: если функции ƒ (М) и g(М) определены на множестве D и имеют в точке Мо этого множества пределы А и В соответственно, то и функции ƒ(М) ± g(M), ƒ(М) • g(М), имеют в точке Мо пределы, которые соответственно равныА ± В, А • В, A /B(В≠0).
43.3. Непрерывность функции двух переменных
Функция z = ƒ(х;у) (или ƒ(М)) называется непрерывной в точке М0(х0;у0), если она:
а) определена в этой точке и некоторой ее окрестности,
в) этот предел равензначению функции z в точке Мо, т. е.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=ƒ(х;у) могут образовывать целые линии разрыва. Так, функция имеет линию разрыва у=х.
Можно дать другое, равносильное приведенному выше, определение непрерывности функции z=ƒ(х;у) в точке. Обозначим Δх=х—х0, Δу=у—у0, Δz=ƒ(х;у)—ƒ(х0;у0). Величины Δх и Δу называются приращениями аргументов х и у, а Δz — полным приращением функции ƒ(х;у) в точке М0(х0;у0).
Функция z = ƒ(х;у) называется непрерывной в точке М0(х0;у0) є D, если выполняется равенствот. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).
43.4. Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной — см. п. 19.5). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
Точка No называется граничной точкой области D, если она не принадлежит D, но в любой окрестности ее лежат точки этой области. Совокупность граничных точек области D называется границей D. Область D с присоединенной к ней границей называется замкнутой областью, обозначается D . Область называется ограниченной, если все ее точки принадлежат неко торому кругу радиуса R. В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координатного угла, а примером ограниченной — ( d -окрестность точки М0(х0;у0).
В случае функции двух переменных, рассматривается некоторое множество упорядоченных пар ( x , y ) , где \(x\in X,\;y\in Y\) .
Если каждой паре (x, y) соответствует только два и более числовых значений z, то считается, что задана функция двух и более переменных. Такая функция будет носить название многозначной.
Она будет записываться следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
z = z ( x , y ) , z = f ( x , y ) , z = F ( x , y )
Существует еще один вариант ее записи:
Функцию z = f ( x , y ) можно изобразить при помощи некоторой поверхности в пространстве в прямоугольной системе. Тогда область определения функции двух переменных будет представлять собой множество точек плоскости, в то же время область функции трех переменных будет представлять собой некоторое множество точек трехмерного пространства.
Функция с любым иным количеством переменных (n) будет определяться аналогичным образом.
Функции нескольких переменных: основные определения
Для более полного понимания, рассмотрим понятия, которые используются для функции нескольких переменных.
Совокупность пар (x, y), являющихся значениями переменных x и y, при которых определена функция, называются ее областью определения.
Независимые переменные (x1, x2, x3, xn) являются аргументами функции.
U — область значений (обозначают: E(u));
u ( \(u \in U\) ) — зависимая переменная (функция).
Существует также такое понятие как производная по направлению — обобщенное понятие производной. Производная по направлению является показателем скорости изменения значения функции при движении в определенном направлении.
Понятие непрерывности функции:
Функция u = f(x) называется непрерывной в точке а, если \(\lim_f(x)=f(a)\) .
Функцию нескольких переменных можно задать четырьмя разными способами:
- словесный;
- табличный;
- аналитический;
- графический.
Аналитический способ в свою очередь подразделяется на два варианта — явный и неявный. Явный способ задания функции нескольких переменных выглядит как формула u = f(x1, x2, x3 . xn), в то время как при неявном способе используется уравнение F(x1, x2, x3 . xn) = 0.
- линия в D(z), имеющая уравнение f(x,y) = C будет называться линией функции;
- проекция на плоскость xOy линии пересечения графика функции z = f(x,y) и плоскости z = C будет называться линией функции.
При этом существует также поверхность уровня функции u = f(x,y,z). Поверхностью называется геометрическое место точек пространства Oxyz, в которых функция принимает одно и то же значение C. Уравнение поверхности уровня выглядит следующим образом:
Наибольшее и наименьшее значение в области
Функция, которая ограничена и дифференцируется в замкнутой области, имеет наибольшее и наименьшее значение либо во внутренних точках этой области, либо на ее границе. Используем пример для рассмотрения алгоритма нахождения наибольшего и наименьшего ее значения.
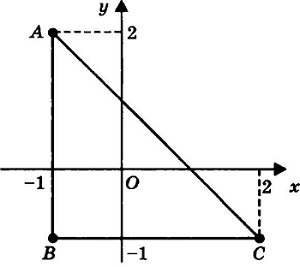
Перед нами функция \(z\;=\;\frac13x^3\;+\;3xy\;+\;\frac13y^3\) в замкнутой области \(х\geq-1,\;у\geq-1,\;х+у\leq1\) .
Следующее действие поможет нам определить стационарные точки функции:
Из этого следует, что стационарные точки функции всего две — O (0, 0) и M (-3, -3). При достижении функции наибольшего или наименьшего значения внутри области, это происходит исключительно в стационарных точках, которые принадлежат данной области. В этом случае имеет смысл рассматривать только точку O (0, 0).
Теперь рассмотрим границу области, состоящую из AB, BC и AC. Необходимо взглянуть на каждый участок в отдельности. Если подставить уравнение участка AB границы x = -1 в функцию:
\(z=\frac13y^3-3y-\frac13\) при \(-1\leq y\leq2\)
Тогда предстоит определить наибольшее и наименьшее значение указанной функции одной переменной на этом отрезке.
Очевидно, что функция принимает наибольшее и наименьшее значение в точке \(y_1 = \sqrt3\) , а также на границе отрезка в точках -1 и 2. Из этого следует, что к точке P нужно добавить точки В(-1, -1), K(-1, \(\sqrt3\) ) и A(-1, 2).
Уравнение участка BC
Функция на этом участке имеет вид
Из этого следует, что достижение наибольшего и наименьшего значения для функции возможно в точке \(x_1 = \sqrt3\) на границе отрезка в точках -1 и 2. Таким образом к выбранным ранее точкам добавятся еще две: К2( \(\sqrt3\) , -1) и С(2, -1)
Уравнение участка AC
x + y = 1 или y = 1 - x
Теперь нужно вновь подставить уравнение этого участка границы в рассматриваемую функцию, учитывая, что \(-1\leq х\leq2\) .
Из этого появляется еще одна точка - M ( \(-\frac12, \frac32\) ).
Теперь предстоит вычислить значение функции в точках A, B, C, K1, K2 K3, O
Выберем из полученных значений наибольшее и наименьшее, они же будут наибольшим и наименьшим значением функции на рассматриваемом множестве.
Наименьшее значение функции достигается на точках \(K_1 и K_2 (-\frac13 — \frac2)\)
Ее наибольшее значение достигается на точке \(B (\frac73)\) .
Примеры решения задач
Пример
Найдем область определения функции двух переменных
Если функция является дробью, то ограничение должно гарантировать, что выполняется следующее условие:
Область определения функции
То есть вся числовая плоскость, за исключением точек двух прямых x=-3, y=5
Изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами: x, y, z. Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных: x, y, z. Если физическое состояние тела к тому же еще и меняется с течением времени t, то та же плотность будет зависеть уже от значений четырех переменных: x, y, z, t.
Определение: Функция трёх переменных имеет вид , при этом переменные называются независимыми переменными или аргументами, переменная называется зависимой переменной или функцией. Например: – функция трёх переменных. Функция трёх переменных подразумевает тот факт, что всё происходит в четырехмерном пространстве. График функции трёх переменных представляет собой так называемую гиперповерхность.
Для функции трёх переменных справедливы правила дифференцирования и таблица производных.
Частные производные . Пусть функция z = f(x,y) определена в некоторой окрестности точки М(x,y). Придадим переменной х произвольное приращение , оставляя значение переменной у неизменным. Тогда функция z = f(x,y) получит приращение , которое называется частным приращением функции по переменной х в точке М(x,y).
Аналогично определяется частное приращение функции по переменной у: .
Определение: Если существует предел ,то он называется частной производной функции z = f(x,y) в точке М по переменной х (по переменной у) и обозначается одним из следующих символов:
Частная производная функции двух переменных по переменной х представляет собой обыкновенную производную функции одной переменной х при фиксированном значении переменной у.
Частная производная функции двух переменных по переменной у представляет собой обыкновенную производную функции одной переменной у при фиксированном значении переменной х.
Пример 1. Найти частные производные функции
Решение: Найдем частную производную функции по переменной х, а переменную у в этом случае будем считать постоянной:
Найдем частную производную функции по переменной у, а переменную х в этом случае будем считать постоянной: .
Полный дифференциал функции. Пусть функция z=f(x,y) определена в некоторой окрестности точки М(x,y). Составим полное приращение функции в точке М:
Функция z = f(x,y) называется дифференцируемой в точке М(x,y), если ее полное приращение можно представить в виде , где и при , . Сумма первых двух слагаемых представляет собой главную часть приращения функции.
Главная часть приращения функции z = f(x,y), линейная относительно и , называется полным дифференциалом функции и обозначается dz: .
Для независимых переменных x и y полагают , . Выражения и называют частными дифференциалами функции.
Теорема (достаточное условие дифференцируемости): Если функция z = f(x,y) имеет в некоторой окрестности точки М(x,y) непрерывные частные производные и , то она дифференцируема в этой точке, причем ее полный дифференциал выражается формулой . (6)
Пример 7. Найти полный дифференциал функции . Решение: Найдем частные производные функции , .
Частным случаем функции многих переменных является функция двух переменных.
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$ в данной области.
Функция двух переменных может быть задана двумя способами:
- аналитический способ (формула; например, $P(x,y)=2\cdot (x+y)$ - периметр прямоугольника);
- табличный способ (двумерная таблица; пример приведен на рис. 1).

Область определения (область существования) функции двух переменных $z=f(x,y)$ - это совокупность пар $(x,y)$, являющихся значениями переменных $x$ и $y$, при которых данная функция определена.
Область определения функции $z=f(x,y)$ может быть изображена на координатной плоскости совокупностью точек $(x,y)$.
Определить и изобразить область определения функции
Решение:
Функция $P(x,y)=2\cdot (x+y)$ определена при любых значениях $(x,y)$.
Следовательно, область определения функции есть вся координатная плоскость $Oxy$ (рис. 2).

Линия, которая ограничивает область определения на плоскости, называется границей области.
Точки области, которые не лежат на границе, называются внутренними точками данной области.
Если область состоит только из внутренних точек (не содержит граничных точек), то она называется открытой (незамкнутой).
Готовые работы на аналогичную тему
Определить и изобразить область определения функции
Решение:
Функция $z=\frac -y^ > > $ определена при любых значениях $(x,y)$, удовлетворяющих неравенству $4-x^ -y^ >0$ или $x^ +y^$ ∠ $4$.
Следовательно, область определения функции есть внутренняя часть круга радиуса $R=2$ с центром в начале координат.
Область определения является открытой, т.е. незамкнутой.

Если область содержит и внутренние точки, и граничные точки, то она называется закрытой (замкнутой).
Определить и изобразить область определения функции
Решение:
Функция $z=\sqrt -y^ > $ определена при любых значениях $(x,y)$, удовлетворяющих неравенству $4-x^ -y^ \ge 0$ или $x^ +y^ \le 4$.
Следовательно, область определения функции есть круг радиуса $R=2$ с центром в начале координат.
Область определения является закрытой, т.е. замкнутой.

Понятие функции нескольких переменных не ограничивается рассмотрением только функции двух переменных. Данное понятие легко обобщается на количество переменных от трех и более.
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Если для каждой совокупности $(x,y,z. t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z. t)$ в данной области.
Обозначение: $w=f(x,y,z. t)$.
Понятие области определения для функции трех и более переменных вводится аналогично соответствующему определению понятия для функции двух переменных.
Графическое изображение функции двух переменных
Функцию двух переменных можно изобразить в пространстве с помощью графика.
Для этого на плоскости $Oxy$ необходимо найти точку $(x,y)$ и восстановить из нее перпендикуляр, на котором отложить отрезок длинной равной $f(x,y)$. Конец отрезка будет являться точкой графика функции (рис.5).

Множество точек графика функции двух переменных образует некоторую поверхность.
Изобразить график функции
Решение:

В пространстве невозможно изобразить с помощью графика функции трех и более переменных.
Функции одной независимой переменной не охватывают все зависимости, существующие в природе. Поэтому естественно расширить известное понятие функциональной зависимости и ввести понятие функции нескольких переменных.
Будем рассматривать функции двух переменных, так как все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.
§43. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
43.1. Основные понятия
Пусть задано множество D упорядоченных пар чисел (х;у). Соответствие ƒ, которое каждой паре чисел (х; у) є D сопоставляет одно и только одно число z є R, называется функцией двух переменных, определенной на множестве D со значениями в Е, и записывается в виде z = ƒ(х;у) или ƒ : D → R При этом х и у называются независимыми переменными (аргументами), а z — зависимой переменной (функцией).
Множество D = D(f) называется областью определения функции. Множество значений, принимаемых z в области определения, называется областью изменения этой функции, обозначается E(f) или Е.
Примером функции двух переменных может служить площадь S прямоугольника со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество 0, у > 0>.
Функцию z = ƒ(х;у), где (х;у) є D можно понимать (рассматривать) как функцию точки М(х;у) координатной плоскости Оху. В частности, областью определения может быть вся плоскость или ее часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается D. Примером замкнутой области является круг с окружностью.
Значение функции z = ƒ(х;у) в точке М0(х0;у0) обозначают z0=ƒ(хо;уо) или z0=ƒ(М0) и называют частным значением функции.
Функция двух независимых переменных допускает геометрическое истолкование. Каждой точке М0(х0; у0) области D в системе координат Oxyz соответствует точка M(x0;y0;z0), где z0 = ƒ(хо;уо) — аппликата точки М. Совокупность всех таких точек представляет собой некоторую поверхность, которая и будет геометрически изображать данную функцию z=ƒ(x;у).
Например, функцияимеет областью определения круг х 2 + у 2 ≤ 1 и изображается верхней полусферой с центром в точке O(0;0;0) и радиусом R = 1 (см. рис. 205).
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: таблицей, аналитически, графиком. Будем пользоваться, как правило, аналитическим способом: когда функция задается с помощью формулы.
43.2. Предел функции
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(х;у) плоскости, координаты которых удовлетворяют неравенствуназывается d -окрестностью точки М0(х0;у0). Другими словами, d -окрестность точки Мо — это все внутренние точки круга с центром Мо и радиусом 8 (см. рис. 206).
Пусть функция z = ƒ(х; у) определена в некоторой окрестности точки М0(х0;у0), кроме, быть может, самой этой точки. Число А называется пределом функции z = ƒ (х; у) при х → х0 и у → у0 (или, что то же самое, при М(х; у) → М0(х0; у0)), если для любого є > 0 существует d > 0 такое, что для всех х ≠ х0 и у ≠ у0 и удовлетворяющих неравенству
выполняется неравенство | ƒ (х; у) — А| → х0 по двум направлениям: справа и слева!)
Геометрический смысл предела функции двух переменных состоит в следующем. Каково бы ни было число є>0, найдется d -окрестность точки Mо(хо;уо), что во всех ее точках М(х;у), отличных от Мо, аппликаты соответствующих точек поверхности z=ƒ(х;у) отличаются от числа А по модулю меньше, чем на є.
Пример 43.1. Найти предел
Решение: Будем приближаться к О(0;0) по прямой у=Кх, где К — некоторое число. Тогда
Функция в точке О(0; 0) предела не имеет, т. к. при разных значенияхК предел функции не одинаков (функция имеет различные предельные значения).
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной (см. п. 17.3). Это означает, что справедливы утверждения: если функции ƒ (М) и g(М) определены на множестве D и имеют в точке Мо этого множества пределы А и В соответственно, то и функции ƒ(М) ± g(M), ƒ(М) • g(М), имеют в точке Мо пределы, которые соответственно равныА ± В, А • В, A /B(В≠0).
43.3. Непрерывность функции двух переменных
Функция z = ƒ(х;у) (или ƒ(М)) называется непрерывной в точке М0(х0;у0), если она:
а) определена в этой точке и некоторой ее окрестности,
в) этот предел равензначению функции z в точке Мо, т. е.
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке), называются точками разрыва этой функции. Точки разрыва z=ƒ(х;у) могут образовывать целые линии разрыва. Так, функция имеет линию разрыва у=х.
Можно дать другое, равносильное приведенному выше, определение непрерывности функции z=ƒ(х;у) в точке. Обозначим Δх=х—х0, Δу=у—у0, Δz=ƒ(х;у)—ƒ(х0;у0). Величины Δх и Δу называются приращениями аргументов х и у, а Δz — полным приращением функции ƒ(х;у) в точке М0(х0;у0).
Функция z = ƒ(х;у) называется непрерывной в точке М0(х0;у0) є D, если выполняется равенствот. е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов х и у стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям — подобные теоремы имели место для функций одной переменной (см. п. 19.4).
43.4. Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной — см. п. 19.5). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
Точка No называется граничной точкой области D, если она не принадлежит D, но в любой окрестности ее лежат точки этой области. Совокупность граничных точек области D называется границей D. Область D с присоединенной к ней границей называется замкнутой областью, обозначается D . Область называется ограниченной, если все ее точки принадлежат неко торому кругу радиуса R. В противном случае область называется неограниченной. Примером неограниченной области может служить множество точек первого координатного угла, а примером ограниченной — ( d -окрестность точки М0(х0;у0).
Читайте также:


