Как сделать функцию линейн в эксель
Это первая статья из серии "Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонности", из которой вы узнаете о 5 способах расчета значений линейного тренда в Excel.
Для того, чтобы легче было научиться прогнозировать продажи с учетом роста и сезонности, я разбил 1 большую статью о расчете прогноза на 3 части:
- Расчет значений тренда (рассмотрим на примере Линейного тренда в этой статье);
- Расчет сезонности;
- Расчет прогноза;
После изучения данного материала вы сможете выбрать оптимальный способ расчета значений линейного тренда, который будет удобен для решения вашей задачи, а в последствии, и для расчета прогноза наиболее удобным для вас способом.
Линейный тренд хорошо применять для временного ряда, данные которого увеличиваются или убывают с постоянной скоростью.
Рассмотрим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.
Временной ряд продажи по месяцам (см. вложенный файл).
В этом временном ряду у нас есть 2 переменных:
Уравнение линейного тренда y(x)=a+bx, где
y — это объёмы продаж
x — номер периода (порядковый номер месяца)
a – точка пересечения с осью y на графике (минимальный уровень);
b – это значение, на которое увеличивается следующее значение временного ряда;
1-й способ расчета значений линейного тренда в Excel с помощью графика
![Расчет прогноза - линейный тренд]()
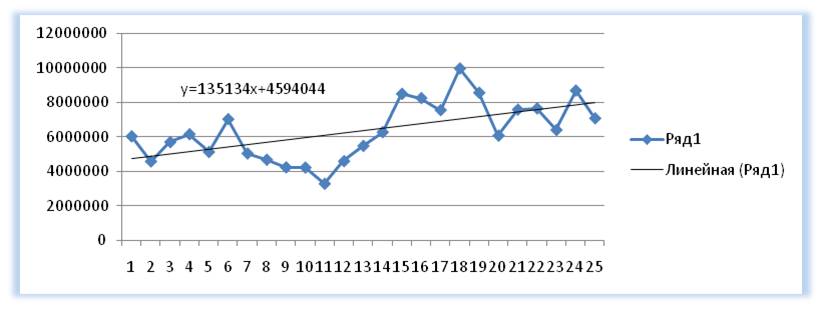
Выделяем анализируемый объём продаж и строим график, где по оси Х — наш временной ряд (1, 2, 3… — январь, февраль, март …), по оси У - объёмы продаж. Добавляем линию тренда и уравнение тренда на график. Получаем уравнение тренда y=135134x+4594044
Для прогнозирования нам необходимо рассчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время - значение по оси Х;
- Значение "a" и "b" уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для каждого периода времени от 1 до 25, а также для будущих периодов с 26 месяца до 36.
Например, для 26 месяца значение тренда рассчитывается по следующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
2-й способ расчета значений линейного тренда в Excel — функция ЛИНЕЙН
1. Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel:
=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)
Для расчета коэффициентов в формулу вводим
известные значения y (объёмы продаж за периоды),
известные значения x (номера периодов),
вместо константы ставим 1,
вместо статистики 0,
Получаем 135135 - значение (b) линейного тренда y=a+bx;
Для того чтобы Excel рассчитал сразу 2 коэффициента (a) и (b) линейного тренда y=a+bx, необходимо
Получаем 135135, 4594044 - значение (b) и (a) линейного тренда y=a+bx;
2. Рассчитаем значения линейного тренда с помощью полученных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов - x, для которых хотим рассчитать значения линейного тренда.
2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также быстрее.
3-й способ расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯРассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новые значения x; конста)
Подставляем в формулу
- известные значения y - это объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
- известные значения x - это номера периодов x для известных значений объёмов продаж y;
- новые значения x - это номера периодов, для которых мы хотим рассчитать значения линейного тренда;
- константа - ставим 1, необходимо для того, чтобы значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
Для того чтобы рассчитать значения тренда для всего временного диапазона, в "новые значения x" вводим диапазон значений X, выделяем диапазон ячеек равный диапазону со значениями X с формулой в первой ячейке и нажимаем клавишу F2, а затем — клавиши CTRL + SHIFT + ВВОД.
4-й способ расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
Рассчитаем значения линейного тренда с помощью стандартной функции Excel:
=ПРЕДСКАЗ(x; известные значения y; известные значения x)
Вместо X поставляем номер периода, для которого рассчитываем значение тренда.
Вместо "известные значения y" - объёмы продаж за анализируемый период (фиксируем диапазон в формуле, выделяем ссылку и нажимаем F4);
"известные значения x" - это номера периодов для каждого выделенного объёма продаж.
3-й и 4-й способ расчета значений линейного тренда быстрее, чем 1 и 2-й, однако с его помощью невозможно управлять коэффициентами тренда, как описано в статье "О линейном тренде".
5-й способ расчета значений линейного тренда в Excel — Forecast4AC PRO
1. Устанавливаем курсор в начало временного ряда, выбираем в настройках программы:
- Что рассчитываем - значения тренда;
- Тренд - Линейный тренд;
- Временной ряд - месячный;
и сохраняем;2. Заходим в меню программы и нажимаем "Start_Forecast". Значения линейного тренда рассчитаны.
Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.
В следующих статье "Как самостоятельно сделать прогноз продаж с учетом роста и сезонности" мы:
О том, что еще важно знать о линейном тренде, вы можете узнать в статье "Что важно знать о линейном тренде".
Точных вам прогнозов!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:
![Novo Forecast - прогноз в Excel - точно, легко и быстро!]()
- Novo Forecast Lite - автоматический расчет прогноза в Excel .
- 4analytics - ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition - BI-системы для анализа и визуализации данных.
Тестируйте возможности платных решений:
- Novo Forecast PRO - прогнозирование в Excel для больших массивов данных.
Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.
Зарегистрируйтесь и скачайте решения
Статья полезная? Поделитесь с друзьями
Комментарии
Цитирую Сергей Иванович К.:
Алексей, добрый день и с наступающим Новым Годом!
У меня давно есть вопрос про линию тренда в Excel. Многие реальные процессы, хорошо описываемые экспонентой, асимптотически стремятся (или растут) не обязательно к (из) оси абсцисс. Линия тренда, построенная в Excel при этом очень сильно отклоняется от реального графика, ибо асимптотически стремится именно к нулю ("растёт" из нуля). Как быть? Нет ли каких то усовершенствований, чтобы можно было использовать формулу вида y=a+b*e^c*x, а то и ещё более универсальную - y=a+b*х+c*e^d*x, т.е. чтобы асимптота могла быть и наклонной?
С уважением, Сергей.Алексей, добрый день и с наступающим Новым Годом!
У меня давно есть вопрос про линию тренда в Excel. Многие реальные процессы, хорошо описываемые экспонентой, асимптотически стремятся (или растут) не обязательно к (из) оси абсцисс. Линия тренда, построенная в Excel при этом очень сильно отклоняется от реального графика, ибо асимптотически стремится именно к нулю ("растёт" из нуля). Как быть? Нет ли каких то усовершенствова ний, чтобы можно было использовать формулу вида y=a+b*e^c*x, а то и ещё более универсальную - y=a+b*х+c*e^d*x , т.е. чтобы асимптота могла быть и наклонной?
С уважением, Сергей.
Сергей, доброе утро. Так захотелось, чтобы думали, а не просто копировали. В разных источниках по разному, есть и mx+b, у нас вот так ) Главное суть!Получим числовые характеристики коэффициентов этого уравнения.
![График линейной аппроксимации]()
Рис 2. График линейной аппроксимации.
![График квадратичной аппроксимации]()
Рис 3. График квадратичной аппроксимации.
![График экспоненциальной аппроксимации]()
Рис 4. График экспоненциальной аппроксимации.
Полученное при построении линии тренда значение коэффициента детерминированности для экспоненциальной зависимости не совпадает с истинным значением (это значение было сосчитано вручную выше) поскольку при вычислении коэффициента детерминированности с помощью функции ЛИНЕЙН используются не истинные значения , а преобразованные значения с дальнейшей линеаризацией.
Назначение функции ЛИНЕЙН
Рассмотрим назначение функции ЛИНЕЙН.
Эта функция использует метод наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные.
Функция возвращает массив, который описывает полученную прямую. Уравнение для прямой линии имеет следующий вид:
y=m1*x1 + m2*x2 + …b или y=m*x + b
где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - это постоянная. Заметим, что y,x и m могут быть векторами.
Функция ЛИНЕЙН возвращает массив . ЛИНЕЙН может также возвращать дополнительную регрессионную статистику.
Получение числовых характеристик зависимости
Для построения числовых характеристик создаем табличную формулу, которая будет занимать 5 строк и 2 столбца (см. таблицу 10).В этот интервал вводим функцию ЛИНЕЙН. Для этого была выполнена следующая последовательность действий:
1. Выделяем область A58:B62.
2. Вызываем Мастера функций.
3. Выбираем функцию ЛИНЕЙН.
4. Определяем аргументы функции:
· В качестве изв_знач_x указываем B2:B16.
· В качестве изв_знач_y указываем C2:C16.
· Третье поле константа оставляем пустым.
· В четвертом поле стат набираем истина.
5. Нажимаем кнопку Закончить.
6. Устанавливаем курсор в строку формул.
7. Нажимаем комбинацию клавиш Ctrl + Shift + Enter, чтобы обеспечить ввод табличной формулы.
Результатом выполнения данных действий является таблица 10.
![]()
Поясним назначение некоторых величин, расположенных в таблице 10.
Величины расположенные в ячейках A58 и B58 характеризуют соответственно наклон и сдвиг.
А58 - коэффициент детерминированности.
А59 - F - наблюдаемое значение.
B60 - число степеней свободы.
A61 - регрессионная сумма квадратов.
B62 - остаточная сумма квадратов.
Далее проверим свои вычисления с помощью программы написанной на языке Turbo Pascal, а для этого составим блок-схему:
Мне нужно определить параметры линейной регрессии.
У меня есть пошаговый пример с картинками:
1. меню ВСТАВКА - пункт ФУНКЦИЯ
2. В окне МАСТЕР ФУНКЦИЙ:
- категория СТАТИСТИЧЕСКИЕ
- в списке выбрать ЛИНЕЙННа картинке у меня представлен пример из устаревшей версии excel, там все функции на русском, а у меня на английском.
![]()
![]()
Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.
Для построения числовых характеристик необходимо создать табличную форму, которая будет занимать 5 строк и 2 столбца. В этот интервал требуется ввести функцию ЛИНЕЙН. Для этого выполняем следующую последовательность действий:
- 1. Выделим область А65:В69.
- 2. Вызовем функцию Линейн.
- 3. Определим аргументы функции
- · В качестве изв_знач_у укажем А3:А27.
- · В качестве изв_знач_х укажем В3:В27.
- · Третье поле Константа оставим пустым.
- · В четвертом поле стат наберем истина.
- 4. Нажмем кнопку ОК.
- 5. Установим курсор в строку формул.
Нажмем комбинацию клавиш Ctrl+Shift+Enter, это обеспечит ввод табличной формулы.
В результате должны заполниться все ячейки интервала А65:В69 (табл.8)
Расчеты по формулам (8) и (10)
![]()
Пояснения к табл. 8:
А67- коэффициент детерминированности
А69- факторная сумма квадратов.
В69- остаточная сумма квадратов.
Рассмотрим назначение функции ЛИНЕЙН.
Эта функция использует метод наименьших квадратов, чтобы определить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные.
Получение числовых характеристик квадратичной зависимости
- 1. Выделим область А71:С75.
- 2. Вызовем Мастер функций.
- 3. Выберем функцию Линейн.
- 4. Определим аргументы функции
- · В качестве изв_знач_у укажем А3:А27.
- · В качестве изв_знач_х укажем В3:В27.
- · Третье поле Константа оставим пустым.
- · В четвертом поле стат наберем истина.
- 5. Нажмем кнопку ОК.
- 6. Установим курсор в строку формул.
Нажмем комбинацию клавиш Ctrl+Shift+Enter. В результате должны заполниться все ячейки интервала А71:С75 (табл.9).
Получение числовых характеристик квадратичной зависимости
![]()
В ячейках А71:С75 введена формула
Получение числовых характеристик экспоненциальной зависимости
- 1. Выделим область А78:В82.
- 2. Вызовем Мастер функций.
- 3. Выберем функцию ЛГРФПРИБЛ.
- 4. Определим аргументы функции
- · В качестве изв_знач_у укажем А3:А27.
- · В качестве изв_знач_х укажем В3:В27.
- · Третье поле Константа оставим пустым.
- · В четвертом поле стат наберем истина.
- 5. Нажмем кнопку ОК.
- 6. Установим курсор в строку формулу.
Нажмем комбинацию клавиш Ctrl+Shift+Enter. В результате должны заполниться все ячейки интервала А78:В82 (см. табл.10).
Получение числовых характеристик экспоненциальной зависимости
![]()
В ячейках А78:В82 введена формула
Сравнивая значения коэффициентов, полученных вручную с табличными, видим отличие в значении (он вычислен в ячейке А78). Это связано с тем, что функция ЛГРФПРИБЛ возвращает параметры для соотношения . То есть . Отсюда следует, что .
Вычисление коэффициента представлено на рис.2.:
Рис. 2. Ячейка А78 Вычисление коэффициента
Для построения числовых характеристик необходимо создать табличную форму, которая будет занимать 5 строк и 2 столбца. В этот интервал требуется ввести функцию ЛИНЕЙН. Для этого выполняем следующую последовательность действий:
- 1. Выделим область А65:В69.
- 2. Вызовем функцию Линейн.
- 3. Определим аргументы функции
- · В качестве изв_знач_у укажем А3:А27.
- · В качестве изв_знач_х укажем В3:В27.
- · Третье поле Константа оставим пустым.
- · В четвертом поле стат наберем истина.
- 4. Нажмем кнопку ОК.
- 5. Установим курсор в строку формул.
Нажмем комбинацию клавиш Ctrl+Shift+Enter, это обеспечит ввод табличной формулы.
В результате должны заполниться все ячейки интервала А65:В69 (табл.8)
Расчеты по формулам (8) и (10)
![]()
Пояснения к табл. 8:
А67- коэффициент детерминированности
А69- факторная сумма квадратов.
В69- остаточная сумма квадратов.
Рассмотрим назначение функции ЛИНЕЙН.
Эта функция использует метод наименьших квадратов, чтобы определить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные.
Получение числовых характеристик квадратичной зависимости
- 1. Выделим область А71:С75.
- 2. Вызовем Мастер функций.
- 3. Выберем функцию Линейн.
- 4. Определим аргументы функции
- · В качестве изв_знач_у укажем А3:А27.
- · В качестве изв_знач_х укажем В3:В27.
- · Третье поле Константа оставим пустым.
- · В четвертом поле стат наберем истина.
- 5. Нажмем кнопку ОК.
- 6. Установим курсор в строку формул.
Нажмем комбинацию клавиш Ctrl+Shift+Enter. В результате должны заполниться все ячейки интервала А71:С75 (табл.9).
Получение числовых характеристик квадратичной зависимости
![]()
В ячейках А71:С75 введена формула
Получение числовых характеристик экспоненциальной зависимости
- 1. Выделим область А78:В82.
- 2. Вызовем Мастер функций.
- 3. Выберем функцию ЛГРФПРИБЛ.
- 4. Определим аргументы функции
- · В качестве изв_знач_у укажем А3:А27.
- · В качестве изв_знач_х укажем В3:В27.
- · Третье поле Константа оставим пустым.
- · В четвертом поле стат наберем истина.
- 5. Нажмем кнопку ОК.
- 6. Установим курсор в строку формулу.
Нажмем комбинацию клавиш Ctrl+Shift+Enter. В результате должны заполниться все ячейки интервала А78:В82 (см. табл.10).
Получение числовых характеристик экспоненциальной зависимости
![]()
В ячейках А78:В82 введена формула
Сравнивая значения коэффициентов, полученных вручную с табличными, видим отличие в значении (он вычислен в ячейке А78). Это связано с тем, что функция ЛГРФПРИБЛ возвращает параметры для соотношения . То есть . Отсюда следует, что .
Вычисление коэффициента представлено на рис.2.:
Рис. 2. Ячейка А78 Вычисление коэффициента
Читайте также: