Как сделать эпюру в экселе
Привет! Сегодня будем учиться строить эпюры поперечных сил. В этой статье я расскажу, что такое поперечная сила, чем интересна и полезна при проведении расчетов на прочность и жесткость. По уже сложившейся традиции, как и с другими эпюрами, будем рассматривать три способа построения эпюры поперечных сил: подробный, упрощенный и быстрый. Для того чтобы рассчитать поперечную силу в сечении нужно уметь пользоваться уравнениями равновесия конструкции. Поэтому перед изучением данной статьи, если вы не знаете этого материала, рекомендую изучить его, перейдя по указанной ссылке выше. Ну что же перейдем непосредственно к обучению!
Эпюра поперечных сил — это график показывающий распределение поперечных сил в сечениях, загруженного элемента, работающего на поперечный изгиб.
Подробный способ построения эпюры поперечных сил
В качестве примера, возьмем балку, частично загрузим ее распределенной нагрузкой q, а часть оставим без нагрузки, чтобы рассмотреть всевозможные случаи:

Первым делом нужно определить все внешние силы, действующие на конструкцию, то есть помимо распределенной нагрузки на балку будет действовать реакции, возникающие в опорах. Если вы до сих пор не умеете их определять, то обязательно изучите этот материал. В этой статье, я подробно на этом останавливаться не буду. Вот какие значения реакций получаться для рассматриваемого примера:




Разбиваем балку на участки
После подготовительного этапа можно приступать к расчету поперечных сил. На отдельных участках балки поперечная сила будет меняться по определенному закону. Как раз, наша задача научиться определять эти законы. Зная закон изменения поперечной силы на участке, можно определить ее значения в любом сечении в пределах этого участка. Так как, поперечная сила меняется по линейному закону, для построения эпюры достаточно определить ординаты на границах участков. Границами участков служат места приложения сосредоточенных сил, а также начало и конец распределенной нагрузки, то есть для нашего случая нужно рассмотреть два участка.

Важно! Для эпюры изгибающих моментов, границей участков также служит место приложения сосредоточенного момента. На эпюру же поперечных сил моменты не оказывают никакого влияния. Однако, так как эпюры поперечных сил и изгибающих моментов строятся, обычно, вместе, то эту границу так же нужно намечать.
Метод сечений
Приступим непосредственно к расчету. Для установления закона изменения поперечной силы, будем использовать метод сечений. Мысленно рассекаем балку на две части, в пределах 1-го участка, на расстоянии x1 от правого торца балки.

Каждую часть балки уравновешиваем путем приложения сосредоточенной силы Qy1 и момента Mx1. Эти силовые факторы, заменяют действие частей балки друг на друга. Для определения этих величин, достаточно рассмотреть равновесие одной из рассеченных частей.

Правила знаков для поперечной силы
Очень важно на данном этапе выбрать правильное направление поперечной силы. Она должна иметь такое направление, при котором часть балки, при неподвижном (закрепленном) противоположном от рассечения месте, стремилась повернутся ПО часовой стрелке.

Также многие авторы рекомендуют просто запомнить такое правило:
- Для правой отсеченной части, направлять поперечную силу вверх;
- Для левой отсеченной части, направлять поперечную силу вниз.
Вводим систему координат для первого участка
Для удобства выберем правую часть, так как здесь меньше нагрузки, которую нужно учитывать в расчете. Также, мы можем не учитывать момент Mx1, так как в этом уроке, нас интересует только поперечная сила. В рассматриваемом сечении вводим локальную систему координат:
- Ось z будет иметь горизонтальное направление;
- Ось y будет направлена вертикально;
- Ось x будет направлена перпендикулярно плоскости чертежа (на нас).

Записываем уравнение равновесия для первого участка и строим эпюру
Для нахождения поперечной силы на первом участке достаточно записать одно уравнение равновесия – сумму проекций все сил на вертикальную ось y. Эта сумма должна быть равна нулю:

Из полученного уравнения, следует:

Таким образом, поперечная сила в пределах первого участка равна 1 кН. Откладываем это значение на графике:

Положительное значение поперечной силы откладывается выше нулевой линии, отрицательное ниже (как в нашем случае). Эпюры штрихуются перпендикулярно нулевой линии, на каждом участке проставляются знаки, на границах участков указываются численные значения.
Расчет второго участка
Проделываем те же действия, что выполняли для первого участка. Рассекаем балку в пределах рассматриваемого участка на расстоянии z2 от левого торца балки:

Зарисовываем отдельно расчетный элемент, отбросив правую часть и заменив ее действие Qy2 и Mx2. Вводим локальную систему координат:
Для того чтобы рассчитать такой участок, с распределенной нагрузкой, воспользуемся хитростью, которой часто пользуются при решении задач по теоретической механике. Свернем эту нагрузку до сосредоточенной силы. Для этого умножим интенсивность q на длину действия нагрузки – z2.

Записываем уравнение равновесия для второго участка:

Выражаем поперечную силу:

Это закон, по которому меняется поперечная сила на втором участке. Чтобы получить значения для построения эпюры, нужно в это уравнение вместо z2 подставить координаты характерных сечений. Как и говорилось ранее, поперечная сила меняется по линейному закону (исключениями могут быть только схемы с трапециевидной нагрузкой), поэтому для построения эпюры достаточно вычислить значения на границах участка. В сечении A (при z2=0) поперечная сила будет равна:

В середине пролета, при z2=2м получим:

По полученным значениям, строим эпюру поперечных сил на втором участке:

Вот собственно и все! Эпюра поперечных сил построена. Согласитесь, длинное руководство получилось?! Так вот, далее я расскажу, как построить эту эпюру намного быстрее, а в конце покажу как это делается за несколько секунд.Сделайте небольшой перерыв на чай, и возвращайтесь к чтению!
Упрощенный способ построения эпюры
Итак, продолжим изучать технологии построения эпюры поперечных сил. В этом методе будем учиться рассчитывать эту эпюру без вынесения отдельных участков балки и без записи уравнений равновесия. Будем выводить сразу следствия из этих уравнений. Также как, в первом случае, балку нужно разбить на 2 участка.
Первый участок
Запишем закон изменения поперечной силы на первом участке. Для этого отметим сечение С, отстающее от правого торца балки на величину z1. Поперечная сила в этом сечении будет равна сумме проекций всех сил на вертикальную ось, находящихся справа (или слева) от сечения. Мы ведем расчет этого участка справа-налево, так как в данном случае справа нагрузки меньше.

Для того чтобы правильно записать уравнение поперечных сил для любого участка, нужно придерживаться следующих правил:

Как видно из уравнения, поперечная сила, на первом участке, не зависит от координаты z1, поэтому во всех сечениях она одинаковая.
Кстати, помните я писал, что нагрузку можно учитывать, как справа, так и слева? Так вот, давайте запишем уравнение, просуммировав нагрузку, находящуюся слева от сечения С и посмотрим результат.
Реакция RA, относительно сечения С, стремится повернуть ПО часовой стрелке, в уравнение пойдет с плюсом:


Подставляя численные значения нагрузки, получим следующий результат:

Теперь перейдем ко второму участку.
Второй участок
Здесь ситуация похожая, подробно комментировать уже не буду, приведу схему и расчет:




По выполненным расчетам двух участков, можно построить уже знакомую эпюру:

Как видите, эпюра поперечных рассчитывается достаточно просто. В последнем разделе я расскажу, как можно построить ее и вовсе устно.
Быстрый способ построения эпюры
Как вы уже, наверное, заметили, эпюра поперечных сил имеет скачки в тех местах, где прикладываются сосредоточенные усилия, а в местах где приложена распределенная нагрузка, эпюра постоянно меняется по линейному закону. Эти свойства эпюры можно использовать при построении. Давайте рассмотрим такую балку:

Определим для нее опорные реакции:

Расчет быстрым способом рекомендую производить слева-направо . В этом случае для скачков эпюры будут следующие правила знаков:
- Если приложенная сила направлена вверх , то и скачек на эпюре будет вверх, на величину силы;
- Если приложенная сила направлена вниз , то и скачек на эпюре будет вниз, на величину силы.
С учетом данных правил, получим вот такую эпюру поперечных сил:

Прокомментирую: в точке А, сила направлена вверх, эпюра поднимается на 4 кН, в точке С, опускается до нуля, т.к. приложенная сила направлена вниз и так далее. С сосредоточенным усилиями думаю все просто и понятно.

Там, где есть, распределенная нагрузка, эпюра меняется не скачкообразно, а постепенно. И чтобы узнать насколько эпюра измениться от действия распределенной нагрузки от ее начала и до конца, нужно умножить интенсивность q на длину ее действия:
Вот собственно и все, что хотелось рассказать об эпюрах поперечных сил! Вы можете задавать любые вопросы по материалам статьи в комментариях ниже. Также рекомендую подписаться на наши соц. сети, чтобы не пропустить новые и интересные материалы.
После освоения данного урока, можете смело приступать к изучению техник построения эпюр изгибающих моментов. Данная статья является продолжением серии статей о том, как строятся эпюры для балок, работающих на поперечный изгиб.


Примеры решения задач на построение эпюр в сопротивлении материалов, строительной и технической механике со всеми расчетами, подробными пояснениями и видеоуроками.
Здесь рассмотрены примеры и порядок расчета значений внутренних силовых факторов, напряжений и перемещений и построения по ним эпюр для всех видов нагружения балок, стержней и валов.
Примеры построения эпюр
При растяжении-сжатии
Примеры построения эпюр внутренних продольных сил, нормальных напряжений и линейных перемещений для стержней при их растяжении и сжатии.
При кручении
Примеры построения эпюр внутренних крутящих моментов и угловых перемещений сечений вала при кручении.
Построение эпюр при изгибе
Примеры построения эпюр внутренних поперечных сил и изгибающих моментов, нормальных и касательных напряжений для балок и рам при изгибе.
Эпюры внутренних силовых факторов
Эпюры напряжений
Наш плейлист с видеоуроками построения эпюр внутренних силовых факторов, напряжений и перемещений для балки:
Порядок построения эпюр
В рассмотренных выше примерах для построения эпюр выполняется следующая последовательность действий:
После построения эпюр желательно выполнять их проверку.
Инструмент Прогрессия дарит нам несколько замечательных возможностей. С помощью него можно заполнить диапазон ячеек данными по определенному закону: в арифметической или геометрической прогрессии. Для этого не нужно даже знать формулы. Для значений в формате дат предусмотрено создание специфических последовательностей.
Инструмент Прогрессия доступен через меню Главная/ Редактирование/ Заполнить/ Прогрессия…

Для начала работы введите начальное значение (первый член) прогрессии. Затем выделите диапазон ячеек, куда будут вводиться данные, и вызовите инструмент.
Числовые последовательности
Арифметическая прогрессия представляет собой числовую последовательность, где каждое число больше (или меньше) предыдущего на одно и тоже значение (шаг).
Примеры:
Арифметическая прогрессия с шагом 2 – это последовательность чисел 1, 3, 5, 7, 9, 11, … В окне инструмента Прогрессия нужно выбрать Арифметическая и установить Шаг равным 2.

Геометрическая прогрессия с шагом 2 – это последовательность чисел 2, 4, 8, 16, …. Этот пример позволяет быстро вспомнить степени 2. В окне инструмента Прогрессия нужно выбрать Геометрическая и установить Шаг равным 2.
Конечно, арифметическую прогрессию 1, 3, 5, 7, 9, 11, … можно организовать путем формулы =А1+2 , а геометрическую 2, 4, 8, 16, … – =А1*2 . Это уже как кому удобнее.
Последовательности дат и рабочих дней
В инструменте Прогрессия есть одна замечательная возможность по заполнению значений в формате дат. Вводим дату, выбираем диапазон,

вызываем инструмент Прогрессия, выбираем Тип Даты, выбираем Единицы Рабочий день.

В итоге получаем диапазон, заполненный только одними рабочими днями (не суббота и не воскресенье).

Если выберем в качестве единиц месяц, то месяц будет прибавляться к начальной дате и т.д. Эти возможности уже за несколько секунд не реализуешь, нужно вспоминать формулы. А если вспомнить, что еще можно и шаг прогрессии задавать, то можно гарантировать, что формула простой не получится.
Изучим как сделать арифметическую и геометрическую прогрессии в Excel, а также в общем случае рассмотрим способы создания числовых последовательностей.
Перед построением последовательностей и различных прогрессий, как обычно, вспомним их детальные определения.
Числовая последовательность — это упорядоченный набор произвольных чисел a1, a2, a3, …, an, … .
Арифметической прогрессией называется такая числовая последовательность, в которой каждый член, начиная со второго, получается из предыдущего добавлением постоянной величины d (также называют шагом или разностью):

Геометрическая прогрессия — это последовательность чисел, в котором каждый член, начиная со второго, получается умножением предыдущего члена на ненулевое число q (также называют знаменателем):

С определениями закончили, теперь самое время перейти от теории к практике.
Арифметическая прогрессия в Excel
Рассмотрим 2 способа задания прогрессии в Excel — с помощью стандартного инструмента Прогрессия и через формулы.
В первом случае на панели вкладок выбираем Главная -> Редактирование -> Заполнить -> Прогрессия:

Далее мы увидим диалоговое окно с настройками параметров:

В данных настройках мы можем выбрать дополнительные параметры, которые позволят нам более детально настроить и заполнить прогрессию в Excel:
- Расположение — расположение заполнения (по столбцам или строкам);
- Тип — тип (арифметическая, геометрическая, даты и автозаполнение);
- Единицы — вид данных (при выборе даты в качестве типа);
- Шаг — шаг (для арифметической) или знаменатель (для геометрической);
- Автоматическое определение шага — автоматическое определение шага, если заданы несколько значений последовательности;
- Предельное значение — ограничение по значению последнего элемента последовательности.
Разберем как сделать арифметическую прогрессию в Excel на конкретном примере.
Создадим набор чисел 3, 7, 11, … , то есть первый элемент равняется 3, а шаг равен 4.
Выделяем диапазон (к примеру, A1:J1) в котором мы хотим разместить набор чисел (диапазон можно и не выделять, однако в этом случае в настройках будет необходимо указать предельное значение), где в первой ячейке будет указан первый элемент (в нашем примере это 3 в ячейке A1), и указываем параметры (расположение, тип, шаг и т.д.):

В результате мы получим заполненный диапазон с заданным набором чисел:

Аналогичный результат можно получить и при задании элементов с помощью формул.
Для этого также задаем начальный элемент в первой ячейке, а в последующих ячейках указываем рекуррентную формулу члена арифметической прогрессии (то есть текущий член получается как сумма предыдущего и шага):

Геометрическая прогрессия в Excel
Принцип построения геометрической прогрессии в Excel аналогичен разобранному выше построению арифметической.
Единственное отличие — в настройках характеристик указываем в качестве типа геометрическую прогрессию.
Например, создадим набор чисел 4, 8, 16, … , то есть первое число равно 4, а каждое последующее в 2 раза больше предыдущего.
Также задаем начальный элемент (4 в ячейке A1), выделяем диапазон данных (например, A1:J1) и указываем параметры:

В итоге получаем:

Идентичного результата также можно добиться и через использование формул:

Числовая последовательность в Excel
Арифметическая и геометрическая прогрессии являются частными случаями числовой последовательности, в общем же случае ее можно создать, как минимум, тремя способами:
- Непосредственное (прямое) перечисление элементов;
- Через общую формулу n-го члена;
- С помощью рекуррентного соотношения, которое выражает произвольный член через предыдущие.
Первый способ подразумевает под собой ручной ввод значений в ячейки. Удобный вариант при вводе небольшого количества значений, в обратном же случае данный способ достаточно трудозатратный.
Второй и третий способы более универсальны, так как позволяют автоматически посчитать значения членов с помощью формул, что удобно при большом количестве элементов.
Поэтому поподробнее остановимся на построении последовательностей данными способами.
Рассмотрим создание числовой последовательности на примере построения обратных чисел к натуральным, то есть набора чисел 1, 1/2, 1/3, … , в котором общая формула n-го члена принимает вид Fn=1/n.
Создадим дополнительный ряд в отдельной строчке, куда для удобства расчета поместим порядковые номера (1, 2, 3 и т.д.), на которые будут ссылаться формулы:

В варианте с рекуррентной формулой рассмотрим пример с набором чисел Фибоначчи, в котором первые два числа равны 1 и 1, а каждый последующее число равно сумме двух предыдущих.
В итоге произвольный член можно представить в виде рекуррентного соотношения Fn = Fn-1 + Fn-2 при n > 2.
Определяем начальные элементы (две единицы) в двух ячейках, а остальные задаем с помощью формулы:
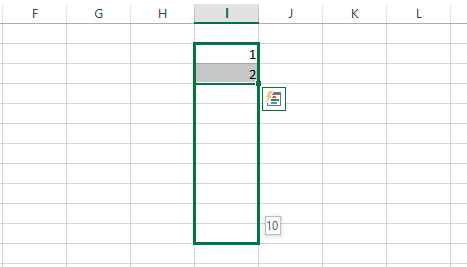
Простейшая арифметическая прогрессия в excel — ввести два первых числа прогрессии (чтобы установить шаг), выделить их, и протащить мышью правый нижний угол выделения до нужной строки
Если записать в соседние ячейки числа, например 1 и 2, то в следующих ячейках появятся значения 4, 5, 6, если записать 500 и 1000, следующими числами будут 1500, 2000 и т.д.
Оба этих числовых ряда будут простейшими арифметическими прогрессиями с заданным шагом — в первом случае с шагом 1, во втором — с шагом 500.
Но, что если мы имеем дело не с простейшей арифметической, а с геометрической прогрессией?
Нет никаких проблем. Введите начальное число в одну из ячеек, а затем выделите диапазон ячеек, в котором и хотите увидеть свою прогрессию.

Инструмент для построения сложных прогрессий в MS Excel
Выбранная вами прогрессия будет мгновенно выведена в пределах выделенного вами диапазона на листе табличного редактора.
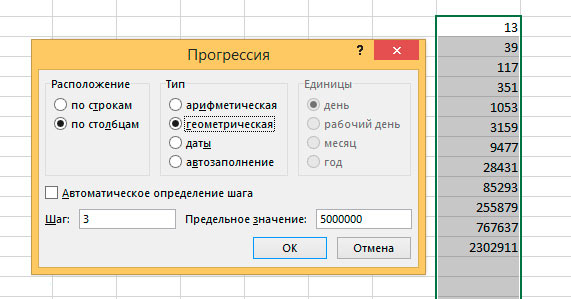
Пример построения геометрической прогрессии с шагом равным 3 и максимальным числом ограниченным 5000000
Рекомендовано УМО по образованию в области строительства в качестве учебного пособия для студентов вузов, обучающихся по направлениям 270100 - "Строительство" и 190200 - "Транспортные машины и транспортно-технологические комплексы"
Сопротивление материалов с примерами решения задач в системе Microsoft Excel: Учебное пособие / А.В. Коргин. - М.: ИНФРА-М, 2012. - 389 с.: ил.; 70x100 1/16. - (Высшее образование). (переплет)
Материал сопровожден вариантами решений практических задач в компьютерной системе электронных таблиц Microsoft Excel с описанием алгоритмов и текстов решений.
1. Решение инженерных задач в системе Microsoft Excel
1.1. Основные сведения, понятия и операции
1.2. Встроенные функции
2. Цели и задачи сопротивления материалов, основные определения
3. Геометрические характеристики поперечных сечений
3.1. Определение геометрических характеристик
3.2. Моменты инерции простых фигур
3.3. Расчет составного сечения
3.4. Расчет составных сечений в системе Excel
4. Внутренние усилия в статически определимых стержневых системах
4.1. Общие положения, определения и правила
4.2. Построение эпюр внутренних усилий в стержневых системах
4.3. Построение эпюр в балках
4.4. Построение эпюр в балках в системе Excel
4.5. Построение эпюр в плоских рамах
4.6. Определение усилий в рамах в системе Excel
4.7. Построение эпюр в криволинейных брусьях
4.8. Определение усилий в криволинейных брусьях в системе Excel
4.9. Определение усилий в плоских фермах
4.10. Определение усилий в плоских фермах в системе Excel
4.11. Пространственные статически определимые рамы
4.12. Определение усилий в пространственных рамах в системе Excel
5. Напряженное состояние
5.1. Основные определения
5.2. Виды напряженного состояния
5.3. Изменение напряжений при повороте площадок
6. Одноосное растяжение-сжатие прямого бруса
6.1. Напряжения и деформации при растяжении-сжатии
6.3. Потенциальная энергия деформаций
6.4. Диаграмма работы материала на растяжение
6.5. Основы расчета конструкций по методу допускаемых напряжений
6.6. Расчет на прочность и жесткость при одноосном растяжении-сжатии по методу допускаемых напряжений
6.7. Основы расчета конструкций по предельным состояниям
6.8. Расчет статически неопределимых стержней на одноосное растяжение-сжатие методом сил
6.9. Расчет стержней на растяжение-сжатие в системе Excel
7.1. Напряжения и деформации при сдвиге
7.2. Закон Гука при сдвиге
7.3. Напряжения на главных площадках при сдвиге
7.4. Потенциальная энергия деформаций при сдвиге
7.5. Связь между модулями упругости -Ей сдвига – G
7.6. Расчет на прочность при сдвиге по методу допускаемых напряжений
8.1. Напряжения и деформации при кручении
8.2. Потенциальная энергия деформаций
8.3. Напряжения в продольных и наклонных сечениях
8.4. Расчет вала на кручение по методу допускаемых напряжений
8.5. Расчет статически неопределимых валов на кручение
8.6. Расчет валов на кручение в системе Excel
8.7. Кручение бруса прямоугольного сечения
8.8. Кручение тонкостенных стержней
8.9. Расчет цилиндрических винтовых пружин с малым шагом
8.10. Расчет упругих (пружинных) опор в жестких балках
8.11. Расчет упругих опор жестких балок в системе Excel
9. Изгиб элементов конструкций
9.1. Чистый изгиб прямого бруса
9.1.1. Деформации и напряжения при чистом изгибе
9.1.2. Расчет прочности балок при чистом изгибе по методу допускаемых напряжений
9.1.3. Потенциальная энергия деформаций при чистом изгибе
9.2. Поперечный изгиб прямого бруса
9.2.1. Деформации и нормальные напряжения при поперечном изгибе
9.2.2. Касательные напряжения при поперечном изгибе
9.2.3. Расчет прочности балок при поперечном изгибе по методу допускаемых напряжений
9.2.4. Потенциальная энергия при поперечном изгибе
9.2.5. Расчет прочности балок на изгиб в системе Excel
9.3. Изгиб плоского кривого бруса
9.3.1. Деформации и напряжения при изгибе кривого бруса
9.3.2. Определение положения нейтрального слоя
9.3.3. Расчет кривого бруса в системе Excel
9.4. Перемещения при изгибе
9.4.1. Определение перемещений методом прямого интегрирования (метод начальных параметров)
9.4.2. Вычисление перемещений в системе Excel
9.4.3. Расчет балок на жесткость при изгибе
9.4.4. Расчет балок на жесткость при изгибе в системе Excel
10. Определение перемещений в общем случае нагружения
10.1. Общее выражение потенциальной энергии бруса
10.2. Определение перемещений с помощью интеграла Мора
10.3. Частные случаи интеграла Мора
10.4. Вычисление интеграла Мора методом Верещагина
10.5. Вычисление перемещений с помощью интеграла Мора в системе Excel
11. Определение внутренних усилий в статически неопределимых стержневых системах
11.1.1. Определение внутренних усилии в неразрезных балках с помощью уравнения 3-х моментов
11.1.2. Расчет неразрезных балок н системе Excel
11.2. Метод перемещений
11.2.1. Определение внутренних усилий в ПЛОСКИХ фермах
11.2.2. Расчет ферм методом перемещений и системе Excel
12. Балка на упругом основании
12.1. Модель упругого основания Винклера
12.2. Дифференциальное уравнение балки на упругом основании
12.3. Балки бесконечной длины
12.4. Балки конечной длины
12.5. Расчет балок на упругом основании в системе Excel
13. Сложное напряженное состояние
13.1. Обобщенный закон Гука
13.2. Потенциальная энергия в общем случае нагружения
13.3. Теории прочности
13.3.1. 3-я теория прочности (пластичности)
13.3.2. 4-я теория прочности (пластичности)
13.3.3. Теория прочности Мора
13.4. Сложное сопротивление прямого бруса
13.4.1. Косой изгиб
13.4.2. Изгиб с кручением
13.4.3. Перемещения бруса в общем случае нагружения
13.4.4. Расчет на сложное сопротивление в системе Excel
13.4.5. Внецентренное растяжение-сжатие прямого бруса
13.4.6. Расчет на внецентренное растяжение-сжатие в системе Excel
14. Расчеты на устойчивость
14.1. Устойчивость центрально сжатого стержня (задача Эйлера)
14.2. Зависимость критической силы от условий закрепления стержня
14.3. Устойчивость стержня при наличии пластических деформаций
14.4. Расчет на прочность при сжатии с учетом устойчивости
14.5. Продольно-поперечный изгиб
14.6. Расчеты на устойчивость в системе Excel
14.6.1. Расчет стержней составного сечения
14.6.2. Расчет ферм
15. Расчеты на усталость
15.1. Общие понятия об усталостном разрушении
15.2. Параметры и виды цикла нагружения
15.3. Предел выносливости конструкционных материалов
15.4. Факторы, влияющие на усталостную прочность
15.5. Расчет на усталость (выносливость)
15.6. Усилия в валах зубчатых и ременных передач
15.7. Расчет валов на выносливость в системе Excel
16. Расчеты на динамические нагрузки
16.1. Общие понятия о динамических нагрузках
16.2. Расчет на действие сил инерции
16.2.1. Линейное движение с ускорением
16.2.2. Вращение стержней с постоянной угловой скоростью
16.2.3. Вращение колец и дисков с постоянной угловой скоростью
16.2.4. Расчеты на действие сил инерции в системе Excel
16.3. Расчет на ударную нагрузку
16.3.1. Расчет при вертикальном падении груза
16.3.2. Учет массы конструкции при вертикальном ударе
16.4. Расчет на колебания
16.4.1. Свободные колебания системы с одной степенью свободы с учетом затухания
16.4.2. Вынужденные колебания системы с одной степенью свободы
16.5. Расчеты на удар и колебания в системе Excel
17. Изгиб и кручение тонкостенного стержня
17.1. Секториальные геометрические характеристики
17.2. Напряжения при нагружении тонкостенного стержня
17.3. Расчет тонкостенных стержней в системе Excel
18. Расчеты конструкций за пределами упругости
18.1. Основы расчета за пределами упругости
18.2. Упругопластический изгиб прямого бруса
18.3. Метод предельных нагрузок
18.4. Расчет статически неопределимых балок методом предельных нагрузок
18.5. Расчет прочности неразрезных балок в системе Excel
19. Контактные напряжения
19.1. Общие понятия о контактных напряжениях
19.2. Давление на упругое полупространство
19.3. Учет формы площадки контакта
19.4. Напряжения в зоне контакта
19.5. Расчет на прочность при контактном воздействии
19.6. Расчет на контактное воздействие в системе Excel
Похожие документы:
Практикум по решению задач на эвм
АЛГОРИТМИЗАЦИЯ И РЕШЕНИЕ ЗАДАЧ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ
. решения задач по математике, физике, экономике, экологии. Содержание обучения Решение задач оптимального планирования и управления в Excel и системах . (сопротивление). Разборка любых старых радиоэлектронных устройств. Основные приемы пайки. Материалы и .
АЛГОРИТМИЗАЦИЯ И РЕШЕНИЕ ЗАДАЧ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ
. решения задач по математике, физике, экономике, экологии. Содержание обучения Решение задач оптимального планирования и управления в Excel и системах . (сопротивление). Разборка любых старых радиоэлектронных устройств. Основные приемы пайки. Материалы и .
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:

Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:

Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.

Рис. 1. Эпюра продольных сил

Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):

Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:

Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.

По полученным данным строим эпюру (рис. 3).

Заключение
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Читайте также:


