Как сделать экспоненциальный график в excel
В этой статье описаны синтаксис формулы и использование функции EXP в Microsoft Excel.
Описание
Возвращает число e, возведенное в указанную степень. Число e равно 2,71828182845904 и является основанием натурального логарифма.
Синтаксис
Аргументы функции EXP описаны ниже.
Число — обязательный аргумент. Показатель степени, в которую возводится основание e.
Замечания
Чтобы вычислить степень с другим основанием, используйте оператор возведения в степень (^).
Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Экспоненциальное распределение. Непрерывные распределения в EXCEL
Рассмотрим Экспоненциальное распределение, вычислим его математическое ожидание, дисперсию, медиану. С помощью функции MS EXCEL ЭКСП.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел и произведем оценку параметра распределения.
Экспоненциальное распределение (англ. Exponential distribution ) часто используется для расчета времени ожидания между случайными событиями. Ниже описаны ситуации, когда возможно применение Экспоненциального распределения :
- Промежутки времени между появлением посетителей в кафе;
- Промежутки времени нормальной работы оборудования между появлением неисправностей (неисправности возникают из-за случайных внешних влияний, а не по причине износа, см. Распределение Вейбулла );
- Затраты времени на обслуживание одного покупателя.
Плотность вероятности Экспоненциального распределения задается следующей формулой:

График плотности распределения вероятности и интегральной функции Экспоненциального распределения выглядит следующим образом (см. ниже).

СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Экспоненциальное распределение тесно связано с дискретным распределением Пуассона . Если Распределение Пуассона описывает число случайных событий, произошедших за определенный интервал времени, то Экспоненциальное распределение должноописывать длину интервала времени между двумя последовательными событиями.
Приведем пример. Предположим, что число машин, прибывающих на парковку днем, описывается распределением Пуассона со средним значением равным 15 машин в час (параметр распределения λ =15). Вероятность того, что на стоянку в течение часа приедет k машин равно:

Т.к. в среднем в час на стоянку приезжает 15 машин, то среднее время между 2-мя приезжающими машинами равно 1час/15машин=0,067. Т.к. среднее время между 2-мя событиями равно обратному значению параметра экспоненциального распределения , то параметр λ =15 , а плотность соответствующего экспоненциального распределения равна:

Экспоненциальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Экспоненциального распределения имеется функция ЭКСП.РАСП() , английское название — EXPON.DIST(), которая позволяет вычислить плотность вероятности (см. формулу в начале статьи) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по экспоненциальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:

Экспоненциальное распределение имеет обозначение Exp ( λ ).
Примечание : До MS EXCEL 2010 в EXCEL была функция ЭКСПРАСП() , которая позволяет вычислить кумулятивную (интегральную) функцию распределения и плотность вероятности . ЭКСПРАСП() оставлена в MS EXCEL 2010 для совместимости.
В файле примера на листе Пример приведены несколько альтернативных формул для вычисления плотности вероятности и интегральной функции экспоненциального распределения :
- =1-EXP(- λ *x) ;
- =ГАММА.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем Гамма распределения ;
- =ВЕЙБУЛЛ.РАСП(x;1;1/ λ ;ИСТИНА) , т.к. экспоненциальное распределение является частным случаем распределения Вейбулла ;
Примечание : Для удобства написания формул в файле примера создано Имя для параметра распределения — λ .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .

Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Генерация случайных чисел
Для генерирования массива чисел, распределенных по экспоненциальному закону , можно использовать формулу =-LN(СЛЧИС())/ λ
Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Если случайные числа содержатся в диапазоне B14:B213 , то оценку параметра экспоненциального распределения λ можно сделать с использованием формулы =1/СРЗНАЧ(B14:B213) .
Задачи
Экспоненциальное распределение широко используется в такой дисциплине как Техника обеспечения надежности (Reliability Engineering). Параметр λ называется интенсивность отказов , а 1/ λ – среднее время до отказа .
Предположим, что электронный компонент некой системы имеет срок полезного использования, описываемый Экспоненциальным распределением с интенсивностью отказа равной 10^(-3) в час, таким образом, λ = 10^(-3). Среднее время до отказа равно 1000 часов. Для того чтобы подсчитать вероятность, что компонент выйдет из строя за Среднее время до отказа, то нужно записать формулу:

Т.е. результат не зависит от параметра λ .
В MS EXCEL решение выглядит так: =ЭКСП.РАСП(10^3; 10^(-3); ИСТИНА)
Задача . Среднее время до отказа некого компонента равно 40 часов. Найти вероятность, что компонент откажет между 20 и 30 часами работы. =ЭКСП.РАСП(30; 1/40; ИСТИНА)- ЭКСП.РАСП(20; 1/40; ИСТИНА)
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Функция EXP (экспонента) в Microsoft Excel

Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
-
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:


Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.





Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.


Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Мы рады, что смогли помочь Вам в решении проблемы.
Отблагодарите автора, поделитесь статьей в социальных сетях.

Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Excel, как универсальный табличный редактор, давно и неплохо справляется с большинством задач прогнозирования (см. список литературы в конце заметки). Однако, не всегда вычисления в Excel являются простыми и понятными. И вот в версии 2016 года разработчики Microsoft добавили семейство функций ПРЕДСКАЗ (FORECAST), которые позволяют в несколько кликов решать большой круг задач прогнозирования на основе экспоненциального сглаживания.
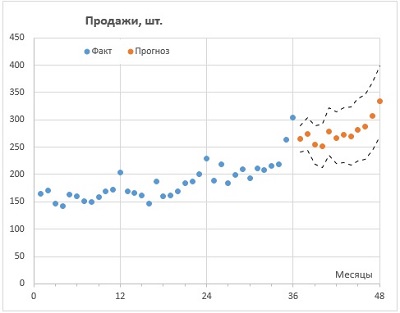
Рис. 1. Прогнозирование продаж в Excel с помощью семейства функций ПРЕДСКАЗ
Об экспоненциальном сглаживании
Экспоненциальное сглаживание также известно, как метод ETS: ошибки (Errors), тренд (Trend), сезонный фактор (Seasonal). Для составления прогноза используются все исторические данные, но коэффициенты, определяющие вклад, убывают в прошлое по экспоненте (отсюда и название). Это позволяет, с одной стороны, чутко реагировать на свежие данных, с другой стороны, сохранять информацию об историческом поведении всего временного ряда. Если данным присущ тренд, он вычисляется в каждой точке данных (а не на основе регрессии всего временного ряда). Наконец, с помощью автокорреляции в данных выявляется сезонность.
Преимущество модели в том, что она не использует никаких предположений относительно характера тренда (или его отсутствия) и периодичности сезонных колебаний (или их отсутствия). Все коэффициенты в модели подбираются на основе минимизации суммы квадратов ошибок, то есть, разности между прогнозом на исторических данных и самих данных. Если вас интересует, как это происходит, рекомендую работу Формана (см. список литературы).
Собственно, оптимизируются три коэффициента:
α – разброс относительно среднего
Разработчики Microsoft не предоставили пользователям возможность влиять на выбор коэффициентов, за исключением периода сезонности (об этом ниже).
Обзор функций семейства ПРЕДСКАЗ
В Excel представлено 5 функций:
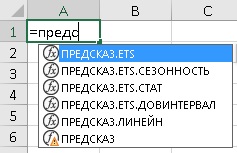
Рис. 2. Семейство функций ПРЕДСКАЗ в Excel
ПРЕДСКАЗ.ETS рассчитывает будущее значение на основе существующих (ретроспективных) данных методом экспоненциального сглаживания. Т.е., дает прогноз одним числом.
ПРЕДСКАЗ.ETS.СЕЗОННОСТЬ возвращает длину повторяющегося фрагмента, обнаруженного в заданном временном ряду. Например, 12, если исторические данные представляют из себя продажи за месяц.
ПРЕДСКАЗ.ETS.СТАТ возвращает восемь статистических значений, являющихся результатом прогнозирования временного ряда. Вряд ли вы будете использовать эту функцию. Она нужна для более тонкого исследования параметров прогнозной модели.
ПРЕДСКАЗ.ЛИНЕЙН вычисляет будущее значение с помощью линейной регрессии исторических данных. До версии 2016 в Excel вместо семейства функций была единственная функция ПРЕДСКАЗ, которая работала также, как и ПРЕДСКАЗ.ЛИНЕЙН. Функция ПРЕДСКАЗ оставлена для обратной совместимости, но скоро перестанет поддерживаться. Далее в заметке ПРЕДСКАЗ.ЛИНЕЙН не рассматривается, так как не относится к функциям, использующим алгоритм экспоненциального сглаживания.
ПРЕДСКАЗ.ETS
В качестве примера рассмотрим месячный пассажиропоток в аэропорту (пример от MS). Исторические данные были собраны за период с января 2009 по декабрь 2912 г.
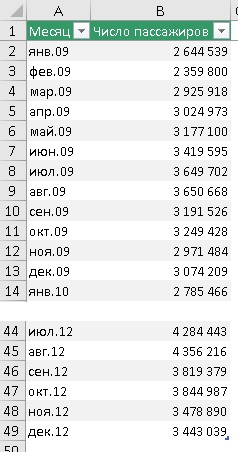
Рис. 3. Исторические данные
Продолжим временную шкалу еще на год, и создадим столбец для прогноза. Обычно прогноз располагают в отдельном столбце для того, чтобы при построении графика представить исторические и прогнозные значения разными линиями.
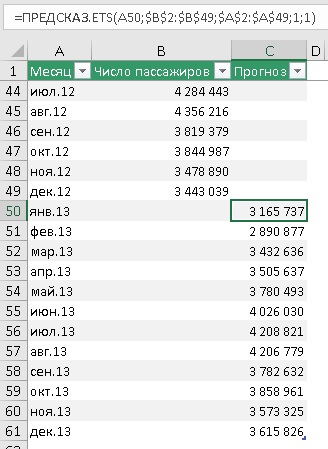
Рис. 4. Прогнозные значения на основе функции ПРЕДСКАЗ.ETS
Подробнее о формуле в ячейке С50:
Первый аргумент – целевая_дата = А50 – янв.13, т.е., в ячейке С50 ищется прогноз пассажиропотока для января 2013 г. Ссылка относительная, что позволит при протягивании функции вниз по столбцу ссылаться на новое значение: в С51 – на А51, в С52 – на А52 и т.д.
Второй аргумент – значения = $B$2:$B$49. Здесь расположены исторические данные пассажиропотока. Ссылка абсолютная, чтобы при протягивании формулы ячейки, на которые ссылаются не изменились.
Третий аргумент – временная_шкала = $A$2:$A$49. Здесь расположены даты временной шкалы или номера периодов. Важно чтобы они отстояли друг от друга на фиксированный интервал. Если интервал не будет фиксированным, Excel всё еще будет исходить из гипотезы, что интервал фиксированный, а некоторые данные пропущены. Как обрабатываются такие ситуации описано ниже. Сортировать массив по значениям временной шкалы не обязательно, так как ПРЕДСКАЗ.ETS сама отсортирует данные прежде, чем выполнить расчеты.
Четвертый аргумент – [сезонность] = 1. Это необязательный аргумент. Значение по умолчанию равно 1. Для него Excel автоматически определяет сезонность и использует положительные целые числа в качестве длины сезонного шаблона. Значение 0 предписывает не использовать фактор сезонности, в результате чего прогноз будет линейным. Если для этого параметра задано положительное целое число, алгоритм использует его в качестве длины шаблона сезонности. Например, вы знаете, что сезонность равна 4 (квартальная периодичность), но предполагаете, что она слабая, и автоматический алгоритм Excel может ее не выявить, и будет считать, что сезонности нет. Для начала я рекомендовал бы использовать значение по умолчанию.
Пятый аргумент – [заполнение_данных] = 1. Это необязательный аргумент. Хотя временная шкала требует постоянный шаг между точками данных, FORECAST.ETS поддерживает до 30% отсутствующих данных и автоматически настраивает их. 0 указывает, что алгоритм учитывает отсутствующие точки в качестве нулей. Если задано значение 1 (вариант по умолчанию), функция определяет отсутствующие значения как среднее между соседними точками.
Шестой аргумент – [агрегирование] – в нашем примере опущен. Это необязательный аргумент. Он нужен, если даты временной шкалы или номера периодов содержат дубли. Функция ПРЕДСКАЗ.ETS выполнит агрегирование точек с одинаковой меткой времени. Параметр агрегирования — это числовое значение, определяющее способ агрегирования нескольких значений с одинаковой меткой времени. Для значения по умолчанию 0 используется метод СРЗНАЧ; также доступны варианты СУММ, СЧЁТ, СЧЁТЗ, МИН, МАКС и МЕДИАНА.
Экспонента – известная математическая функция. В Excel её можно рассчитать при помощи оператора EXP.
Для чего буква Е в записи числа в Excel
Е — экспоненциальный формат записи числа. Служит для записи очень больших и очень малых чисел. Удобен для действий над такими числами. Используется, например, в калькуляторах, в которых нет возможности отобразить большое число. Например:
2134123412341230000000000000000000 = 2,13412341234123E+33
Ноябрьское обновление 2021:
Теперь вы можете предотвратить проблемы с ПК с помощью этого инструмента, например, защитить вас от потери файлов и вредоносных программ. Кроме того, это отличный способ оптимизировать ваш компьютер для достижения максимальной производительности. Программа с легкостью исправляет типичные ошибки, которые могут возникнуть в системах Windows – нет необходимости часами искать и устранять неполадки, если у вас под рукой есть идеальное решение:

Так как мы можем найти символ +, -, *, / соответствующий на клавиатуре, мы также можем использовать символ ^ для применения экспоненциальных вычислений. Как и 10 ^ 2, он представляет 10 со степенью 2, и результатом вычисления является 100, поэтому мы можем использовать его следующим образом:
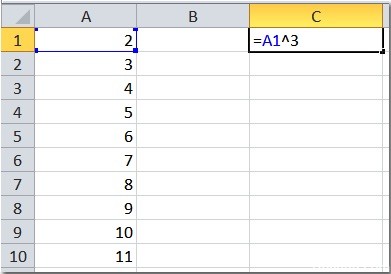
- Введите следующую формулу в соседнем пустом поле C1: = A1 ^ 3
- Затем нажмите клавишу ввода и выберите ячейку C1, затем передвиньте ручку заполнения в C10. Вы увидите следующие результаты:
- Поскольку это формулы, вставьте их как значения, если вам нужно скопировать их в другие ячейки.
Что нужно иметь в виду об экспоненциальной функции (EXP) в Excel
Экспоненциальная функция в Excel часто используется с функцией журнала, например, если мы хотим найти скорость роста или уменьшения, мы будем использовать функции EXP и LOG вместе.
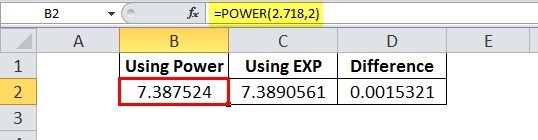
Мы также можем использовать функцию POWER вместо экспоненциальной функции в Excel, но единственным отличием является точность измерения. При использовании функции POWER ее можно указать от e до 2.71 или до десятичных разрядов 3-4, но функция EXP в Excel обычно принимает значение от e до десятичных разрядов 9.
Таким образом, если вы вычисляете экспоненту в серии Excel для работы с нелинейными экспоненциальными функциями, экспоненциальное значение которых у нас есть, лучше использовать функцию EXP в Excel, чем функцию POWER.
В случае сложных показателей, например = EXP (- (2.2 / 9.58) ^ 2), необходимо соблюдать осторожность с помощью скобок, если скобки перепутаны, выходные данные могут отличаться от фактических выходных данных, поэтому это должно быть = EXP (- ((2.2 / 9.58) ^ 2)).
РЕКОМЕНДУЕМЫЕ: Нажмите здесь, чтобы устранить ошибки Windows и оптимизировать производительность системы

CCNA, веб-разработчик, ПК для устранения неполадок
Я компьютерный энтузиаст и практикующий ИТ-специалист. У меня за плечами многолетний опыт работы в области компьютерного программирования, устранения неисправностей и ремонта оборудования. Я специализируюсь на веб-разработке и дизайне баз данных. У меня также есть сертификат CCNA для проектирования сетей и устранения неполадок.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
-
Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:

Для выполнения расчета щелкаем по кнопке Enter. Итог выводится в заранее указанную ячейку.

Урок: Другие математические функции в Эксель
Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.



После вышеперечисленных действий результат расчета будет показан в той ячейке, которая была выделена в первом пункте данного способа.


Урок: Мастер функций в Microsoft Excel
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.

После того, как тип графика выбран, программа построит и отобразит его на том же листе, согласно указанным экспонентам. Далее его можно будет редактировать, как и любую другую диаграмму Экселя.

Урок: Как сделать график в Excel
Как видим, рассчитать экспоненту в Экселе при помощи функции EXP элементарно просто. Эту процедуру легко произвести как в ручном режиме, так и посредством Мастера функций. Кроме того, программа предоставляет инструменты для построения графика на основе этих расчетов.

Мы рады, что смогли помочь Вам в решении проблемы.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
Дополнительные сведения
Вы всегда можете задать вопрос специалисту Excel Tech Community, попросить помощи в сообществе Answers community, а также предложить новую функцию или улучшение на веб-сайте Excel User Voice.
Excel works!
Thanks for Visiting

Экспонента в Excel. Что такое экспонента и как применять?
Мы немного затронули тему экспоненты в статье про округление больших чисел . В этой же статье мы обсудим, что же такое экспонента в Excel и, самое главное, для чего она может пригодиться в обычной жизни или в бизнесе.
Экспонента. Что это такое?
Мы знаем, что наш мир описан точными науками — т.е. набором правил и законов более-менее точно описывающих происходящее. Для этого в большинстве случаев помогают функции/формулы. В природе довольно часто встречаются экспоненциальные явления (описываем экспонентой) формулой с числом e, а у = e в степени x уже будет экспоненциальной функцией:
Число e — это т.н. число Эйлера, приблизительно равное 2,72. Примечательно оно тем, что производная от этой функции равна самой функции exp(x)` = exp(x).
Что это вообще такое, и что для нас означает?
Лучше всего, действие экспоненты показывают графики ниже:
Две функции: y = 2 в степени x и y = e в степени x , где x = время, к примеру. Мы видим, что скорость роста экспоненциального графика увеличивается быстрее. А все почему? Потому, что производная (скорость роста или уменьшения) функции равна самой функции, т.е. скорость увеличения функции равна значению функции.
Если грубо, то в природе, это действительно встречается часто — чем больше клеток делятся, тем быстрее их становиться больше. Чем больше у вас денег в банке, тем большую прибыль они приносят. Например:
Вы вложили 1 000 руб. в банк, через год они принесли свои 100 руб. процентами, еще через год на вас работают уже 2 работника 1 000 руб. и 100 руб. и так далее пока вы не заберете деньги или не случится банковский кризис.
Кстати население на планете Земля тоже растет по экспоненте;)
Принцип Парето и экспонента
20% любителей пива употребляют 80% всего пива
На принципе Парето построен и ABC анализ запасов, например.
Этот принцип Парето — еще один пример экспоненты.
Экспонента в Excel
Когда по смыслу функции более-менее объяснил, напишу как считать ее и есть ли функция экспонента в Excel. Само собой есть.
В Эксель все посчитать несложно:
или можно число возвести в степень
Дополнение. Как запомнить 15 знаков числа е?
В качестве отвлечения привожу способ, как запомнить число e c точностью до 15 знаков
- запишите 2,7,
- затем дважды год рождения Льва Толстого – 1828,
- затем величины углов равнобедренного прямоугольного треугольника – 45°, 90°, 45°,
- в итоге получается: 2,718281828459045.
Как фанат Льва Николаевича, я не смог забыть этот способ 🙂 Кстати отличная книга о том как запоминать много информации и как работает память здесь .
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью экспоненциальной функции.
Метод наименьших квадратов (англ. Ordinary Least Squares, OLS) является одним из базовых методов регрессионного анализа в части оценки неизвестных параметров регрессионных моделей по выборочным данным. Основная статья про МНК – МНК: Метод Наименьших Квадратов в MS EXCEL.
В этой статье рассмотрена только экспоненциальная зависимость, но ее выводы можно применить и к показательной зависимости, т.к. любую показательную функцию можно свести к экспоненциальной:
y=a*m x =a*(e ln(m) ) x = a*e x*ln(m) =a*e bx , где b= ln(m))
В свою очередь экспоненциальную зависимость y=a*EXP(b*x) при a>0 можно свести к случаю линейной зависимости с помощью замены переменных (см. файл примера ).
После замены переменных Y=ln(y) и A=ln(a) вычисления полностью аналогичны линейному случаю Y=b*x+A. Для нахождения коэффициента a необходимо выполнить обратное преобразование a= EXP(A) .

Следствием замены Y=ln(y) и A=ln(a) являются дополнительные ограничения: a>0 и y>0. При уменьшении х (в сторону больших по модулю отрицательных чисел) соответствующее значение y асимптотически стремится к 0. Именно такую линию тренда и строит инструмент диаграммы Линия тренда. Если среди значений y есть отрицательные, то с помощью инструмента Линия тренда экспоненциальную линию тренда построить не удастся.
Чтобы обойти это ограничение используем другое уравнение экспоненциальной зависимости y=a*EXP(b*x)+с, где по прежнему a>0, т.е. при росте х значения y также будут увеличиваться. В качестве с можно взять некую заранее известную нижнюю границу для y, ниже которой у не может опускаться, т.е. у>с. Далее заменой переменных Y=ln(y-c) и A=ln(a) опять сведем задачу к линейному случаю (см. файл примера лист Экспонента2 ).

Если при росте х значения y уменьшаются по экспоненциальной кривой, т.е. a файл примера лист Экспонента3 ).
См. также
Примечание: Эта страница переведена автоматически, поэтому ее текст может содержать неточности и грамматические ошибки. Для нас важно, чтобы эта статья была вам полезна. Была ли информация полезной? Для удобства также приводим ссылку на оригинал (на английском языке).
Пользовательский числовой формат не влияет на вычисления, меняется лишь отображения числа в ячейке. Пользовательский формат можно ввести через диалоговое окно Формат ячеек, вкладка Число, (все форматы), нажав CTRL+1. Сам формат вводите в поле Тип, предварительно все из него удалив.

Точки с запятой разделяют части формата: формат для положительных значений; для отрицательных значений; для нуля. Для описания формата используют специальные символы.
Третья часть формата – для отображения нуля. В принципе, вместо 0 можно указать любой символ или несколько символов (см. статью Отображение в MS EXCEL вместо 0 другого символа).
Например, формат 0;
Как привести число с Е к привычному виду в Excel, OpenOffice или LibreOffice
Как на скриншоте выше — выбрать соответствующий формат в блоке Число на вкладке Главное для Excel 2019. Выделяем нужные ячейки и меняем формат. Для других версий или таблиц других производителей будет как на скриншотах ниже.
Убираем Е в Excel
Правым кликом по выделенной ячейке или группе вызываем меню, в котором выбираем Формат ячеек…
В окне Формат ячеек выбираем необходимое Число десятичных знаков.
Убираем Е в OpenOffice
Тем же правым кликом на выделенных ячейках вызываем меню где выбираем Формат ячеек и устанавливаем дробную часть. Видите, в ячейке D4 число с E, а в D7 уже привычное нам число.
Убираем Е в LibreOffice
Всё точно так же как в OpenOffice. Формат сам перестроится после того как вы укажете дробную часть. Формат Standart (или Общий для Excel) отобразит данные в стандартном виде, то есть с E.
Если нужно получить больше знаков в целой части числа c E, то выбираем шаблон подходящего формата и дописываем в него нули до необходимого количества знаков целого числа до запятой.
Теперь выясним всё про константу e и экспоненту.
Что такое число e или EXP (функция EXP)
Константа e , иногда называемая числом Эйлера , приблизительно равна 2,718 и является основанием натурального логарифма. Это не E.
Экспонента — показательная функция y=ex, где е — число Эйлера.
Ниже о числе e и о том, как просчитать вероятность, что меня в классе не вызовут к доске в течении месяца. Немного лукаво применительно к практике — выбор ученика не случаен.
Описание функции EXP (функция EXP) в Excel для Microsoft 365 Excel для Microsoft 365 для Mac.
В Excel сложение, вычитание, умножение и деление являются базовыми вычислениями, вы можете использовать их быстро и легко. Но иногда вам нужно выполнить экспоненциальный расчет для определенного числа ячеек, как вы можете применить экспоненциальный расчет в Excel?

Excel имеет экспоненциальный Функция Excel называется функцией EXP, которая классифицируется как функция Math / Trig, которая возвращает числовое значение, равное e, которое увеличивается силой данного числа.
Выполнение экспоненциального вычисления для числа - это ячейка в Excel с функцией Power.
Мы можем вычислить экспоненциальное значение числа в конкретной ячейке, используя функцию Power. Формула для функции Power выглядит следующим образом:
куда - это местоположение ячейки, для которой необходимо вычислить экспоненциальное значение, и - для которого должно быть вычислено экспоненциальное значение.
Обратите внимание, что после запятой в формуле есть пробел.
Например, если нам нужно найти экспоненциальное значение степени 2 для числа в ячейке A3, формула принимает вид:
Введите формулу в ячейку, в которой вы хотите отобразить экспоненциальное значение. Предположим, что ячейка, в которой мы хотим иметь значение ячейки C3. Нажмите Enter, чтобы отобразить экспоненциальное значение в ячейке C3.

Примените экспоненциальный расчет к диапазону ячеек с символом ^.
Обновление за январь 2022 года:
Теперь вы можете предотвратить проблемы с ПК с помощью этого инструмента, например, защитить вас от потери файлов и вредоносных программ. Кроме того, это отличный способ оптимизировать ваш компьютер для достижения максимальной производительности. Программа с легкостью исправляет типичные ошибки, которые могут возникнуть в системах Windows - нет необходимости часами искать и устранять неполадки, если у вас под рукой есть идеальное решение:

Так как мы можем найти символ +, -, *, / соответствующий на клавиатуре, мы также можем использовать символ ^ для применения экспоненциальных вычислений. Как и 10 ^ 2, он представляет 10 со степенью 2, и результатом вычисления является 100, поэтому мы можем использовать его следующим образом:
- Введите следующую формулу в соседнем пустом поле C1: = A1 ^ 3
- Затем нажмите клавишу ввода и выберите ячейку C1, затем передвиньте ручку заполнения в C10. Вы увидите следующие результаты:
- Поскольку это формулы, вставьте их как значения, если вам нужно скопировать их в другие ячейки.

Что нужно иметь в виду об экспоненциальной функции (EXP) в Excel
Экспоненциальная функция в Excel часто используется с функцией журнала, например, если мы хотим найти скорость роста или уменьшения, мы будем использовать функции EXP и LOG вместе.
Мы также можем использовать функцию POWER вместо экспоненциальной функции в Excel, но единственным отличием является точность измерения. При использовании функции POWER ее можно указать от e до 2.71 или до десятичных разрядов 3-4, но функция EXP в Excel обычно принимает значение от e до десятичных разрядов 9.
Таким образом, если вы вычисляете экспоненту в серии Excel для работы с нелинейными экспоненциальными функциями, экспоненциальное значение которых у нас есть, лучше использовать функцию EXP в Excel, чем функцию POWER.

В случае сложных показателей, например = EXP (- (2.2 / 9.58) ^ 2), необходимо соблюдать осторожность с помощью скобок, если скобки перепутаны, выходные данные могут отличаться от фактических выходных данных, поэтому это должно быть = EXP (- ((2.2 / 9.58) ^ 2)).
CCNA, веб-разработчик, ПК для устранения неполадок
Я компьютерный энтузиаст и практикующий ИТ-специалист. У меня за плечами многолетний опыт работы в области компьютерного программирования, устранения неисправностей и ремонта оборудования. Я специализируюсь на веб-разработке и дизайне баз данных. У меня также есть сертификат CCNA для проектирования сетей и устранения неполадок.
Читайте также:


