Как сделать чтобы параллельные прямые пересеклись
Тот случай, когда зал подпевает хором. Две прямые могут:
1) совпадать;
2) быть параллельными: ;
3) или пересекаться в единственной точке: .
Справка: – это математический знак пересечения.
Как определить взаимное расположение двух прямых?
Начнём с первого случая:
Рассмотрим прямые и составим три уравнения из соответствующих коэффициентов: . Из каждого уравнения следует, что , следовательно, данные прямые совпадают.
Второй случай, когда прямые параллельны:
2) Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных и пропорциональны: , но
В качестве примера рассмотрим прямые . Сначала проверяем пропорциональность соответствующих коэффициентов при переменных :
Однако совершенно очевидно, что .
Вывод:
И третий случай, когда прямые пересекаются:
Так, оставим систему для прямых :
Из первого уравнения следует, что , а из второго уравнения: , значит, система несовместна (нет решений). Таким образом, коэффициенты при переменных не пропорциональны.
Вывод: прямые пересекаются
Задача 74
Выяснить взаимное расположение прямых:
Решение основано на исследовании направляющих векторов прямых:
а) Из уравнений найдём направляющие векторы прямых: .
Вычислим определитель, составленный из координат данных векторов:
, значит, векторы не коллинеарны и прямые пересекаются.
Вопрос: всё ли вам понятно? Если нет, то используйте три ссылки выше. Ну а остальные перепрыгивают камень и следуют дальше, прямо к Кащею Бессмертному =)
б) Найдем направляющие векторы прямых :
– прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают (тут и определитель считать не надо).
Очевидно, что коэффициенты при переменных пропорциональны и .
Выясним, справедливо ли равенство :
в) Найдем направляющие векторы прямых :
Вычислим определитель, составленный из координат данных векторов:
, следовательно, направляющие векторы коллинеарны и прямые либо параллельны, либо совпадают.
Теперь выясним, справедливо ли равенство . Оба свободных члена нулевые, поэтому:
Полученное значение удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).
Таким образом, прямые совпадают.
Ответ:
Очень скоро вы научитесь (или даже уже научились) решать рассмотренную задачу устно и буквально в считанные секунды – присмотрелись к уравнениям, и всё понятно.
7 февраля 1832 года Николай Лобачевский представил на суд коллег свой первый труд по неевклидовой геометрии. Этот день стал началом переворота в математике, а работа Лобачевского - первым шагом к теории относительности Эйнштейна. Сегодня "РГ" собрала пятерку самых распространенных заблуждений о теории Лобачевского, бытующих среди далеких от математической науки людей
Миф первый. Геометрия Лобачевского не имеет ничего общего с Евклидовой.
На самом деле геометрия Лобачевского не слишком сильно отличается от привычной нам Евклидовой. Дело в том, что из пяти постулатов Евклида четыре первых Лобачевский оставил без изменения. То есть он согласен с Евклидом в том, что между двумя любыми точками можно провести прямую, что ее всегда можно продолжить до бесконечности, что из любого центра можно провести окружность с любым радиусом, и что все прямые углы равны между собой. Не согласился Лобачевский только с пятым, наиболее сомнительным с его точки зрения постулатом Евклида. Звучит его формулировка чрезвычайно мудрено, но если переводить ее на понятный простому человеку язык, то получается, что, по мнению Евклида, две непараллельные прямые обязательно пересекутся. Лобачевский сумел доказать ложность этого посыла.
Миф второй. В теории Лобачевского параллельные прямые пересекаются
Это не так. На самом деле пятый постулат Лобачевского звучит так: "На плоскости через точку, не лежащую на данной прямой, проходит более чем одна прямая, не пересекающая данную". Иными словами, для одной прямой можно провести как минимум две прямые через одну точку, которые не будут ее пересекать. То есть в этом постулате Лобачевского речи о параллельных прямых вообще не идет! Говорится лишь о существовании нескольких непересекающихся прямых на одной плоскости. Таким образом, предположение о пересечении параллельных прямых родилось из-за банального незнания сути теории великого российского математика.
Миф третий. Геометрия Лобачевского - единственная неевклидова геометрия
Неевклидовы геометрии - это целый пласт теорий в математике, где основой является отличный от Евклидова пятый постулат. Лобачевский, в отличие от Евклида, к примеру, описывает гиперболическое пространство. Существует еще теория, описывающая сферическое пространство - это геометрия Римана. Вот в ней-то как раз параллельные прямые пересекаются. Классический тому пример из школьной программы - меридианы на глобусе. Если посмотреть на лекало глобуса, то окажется, что все меридианы параллельны. Меж тем, стоит нанести лекало на сферу, как мы видим, что все ранее параллельные меридианы сходятся в двух точках - у полюсов. Вместе теории Евклида, Лобачевского и Римана называют "три великих геометрии".
Миф четвертый. Геометрия Лобачевского не применима в реальной жизни
Напротив, современная наука приходит к пониманию, что Евклидова геометрия - лишь частный случай геометрии Лобачевского, и что в реальный мир точнее описывается именно формулами русского ученого. Сильнейшим толчком к дальнейшему развитию геометрии Лобачевского стала теория относительности Альберта Эйнштейна, которая показала, что само пространство нашей Вселенной не является линейным, а представляет собой гиперболическую сферу. Между тем, сам Лобачевский, несмотря на то, что всю жизнь работал над развитием своей теории, называл ее "воображаемой геометрией".
Миф пятый. Лобачевский первым создал неевклидову геометрию
Это не совсем так. Параллельно с ним и независимо от него к подобным выводам пришли венгерский математик Янош Бойяи и знаменитый немецкий ученый Карл Фридрих Гаусс. Однако труды Яноша не были замечены широкой публикой, а Карл Гаусс и вовсе предпочел не издаваться. Поэтому именно наш ученый считается первопроходцем в этой теории. Однако существует несколько парадоксальная точка зрения, что первым неевклидову геометрию придумал сам Евклид. Дело в том, что он самокритично считал свой пятый постулат не очевидным, поэтому большую часть из своих теорем он доказал, не прибегая к нему.
Ни в какой. По определению прямые называются параллельными, если они не пересекаются. Точка. Если они пересекаются, то они не параллельные.
Заблуждение возникло в связи с пятвм постулатом, который дает возможность в евклидоаоц геометрии выделчть классы эквивалентномти параллельных прямых, потому что легко выводится, что если прямая l параллельна прямым m и n, то прямы m и n также параллельны. Это называется своймтвом транзитивность.
Так вот в геометрии Лобачевского если прямая l параллельна прямым m и n, то нет никакой гарантии, что сами m и n не пересекаются.

Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
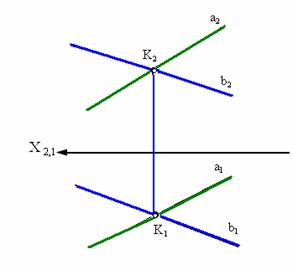
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
.
Рис. 3.4. Пересекающиеся прямые
2. Параллельные прямые
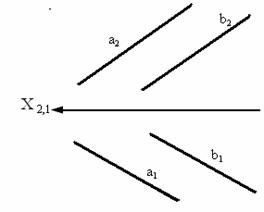
На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
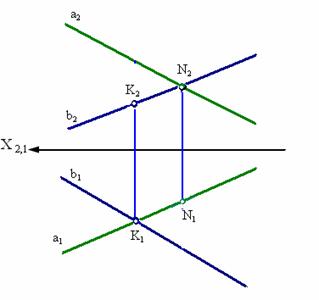
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).
.
Рис. 3.5. Изображение параллельных прямых
.
Читайте также:


