Как сделать чтобы отражался звук
На границе между двумя разными средами часть звуковой волны отражается, а часть проходит дальше.
При переходе звука из воздуха в воду 99,9 % звуковой энергии отражается назад, однако давление в прошедшей в воду звуковой волне оказывается почти в 2 раза больше, чем в воздухе. Слуховой аппарат рыб реагирует именно на это. Поэтому, например, крики и шумы над поверхностью воды являются верным способом распугать морских обитателей. Человека же, оказавшегося под водой, эти крики не оглушат: при погружении в воду в его ушах останутся воздушные пробки, которые и спасут его от звуковой перегрузки.
При переходе звука из воды в воздух снова отражается 99,9 % энергии. Но если при переходе из воды в воздух звуковое давление увеличивалось, то теперь оно, наоборот, резко уменьшается. Именно по этой причине человек, находящийся над водой, не слышит звук, возникающий под водой при ударе одним камнем о другой.
Звук, как и цвет, люди воспринимают по-разному. Например, то, что кажется слишком громким или некачественным одним, может быть нормальным для других.
Для работы над Яндекс.Музыкой нам всегда важно помнить о разных тонкостях, которые таит в себе звук. Что такое громкость, как она меняется и от чего зависит? Как работают звуковые фильтры? Какие бывают шумы? Как меняется звук? Как люди его воспринимают.

Мы довольно много узнали обо всём этом, работая над нашим проектом, и сегодня я попробую описать на пальцах некоторые основные понятия, которые требуется знать, если вы имеете дело с цифровой обработкой звука. В этой статье нет серьёзной математики вроде быстрых преобразований Фурье и прочего — эти формулы несложно найти в сети. Я опишу суть и смысл вещей, с которыми придётся столкнуться.
Поводом для этого поста можете считать то, что мы добавили в приложения Яндекс.Музыки возможность слушать треки в высоком качестве (320kbps). А можете не считать. Итак.
Прежде всего разберёмся с тем, что такое цифровой сигнал, как он получается из аналогового и откуда собственно берётся аналоговый сигнал. Последний максимально просто можно определить как колебания напряжения, возникающие из-за колебаний мембраны в микрофоне.
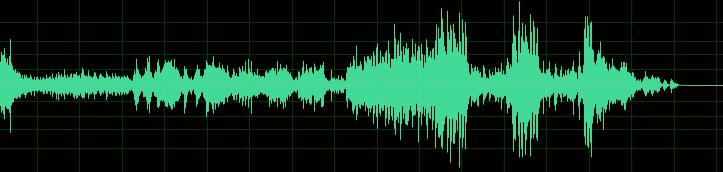
Рис. 1. Осциллограмма звука
Это осциллограмма звука — так выглядит аудио сигнал. Думаю, каждый хоть раз в жизни видел подобные картинки. Для того чтобы понять, как устроен процесс преобразования аналогового сигнала в цифровой, нужно нарисовать осциллограмму звука на миллиметровой бумаге. Для каждой вертикальной линии найдем точку пересечения с осциллограммой и ближайшее целое значение по вертикальной шкале — набор таких значений и будет простейшей записью цифрового сигнала.
Воспользуемся этим интерактивным примером, чтобы разобраться в том, как накладываются друг на друга волны разной частоты и как происходит оцифровка. В левом меню можно включать/выключать отображение графиков, настраивать параметры входных данных и параметры дискретизации, а можно просто двигать контрольные точки.
На аппаратном уровне это, разумеется, выглядит значительно сложнее, и в зависимости от аппаратуры сигнал может кодироваться совершенно разными способами. Самым распространённым из них является импульсно-кодовая модуляция, при которой записывается не конкретное значение уровня сигнала в каждый момент времени, а разница между текущим и предыдущим значением. Это позволяет снизить количество бит на каждый отсчёт примерно на 25%. Этот способ кодирования применяется в наиболее распространённых аудио-форматах (WAV, MP3, WMA, OGG, FLAC, APE), которые используют контейнер PCM WAV.
В реальности для создания стерео-эффекта при записи аудио чаще всего записывается не один, а сразу несколько каналов. В зависимости от используемого формата хранения они могут храниться независимо. Также уровни сигнала могут записываться как разница между уровнем основного канала и уровнем текущего.
Обратное преобразование из цифрового сигнала в аналоговый производится с помощью цифро-аналоговых преобразователей, которые могут иметь различное устройство и принципы работы. Я опущу описание этих принципов в данной статье.
Как известно, цифровой сигнал — это набор значений уровня сигнала, записанный через заданные промежутки времени. Процесс преобразования непрерывного аналогового сигнала в цифровой сигнал называется дискретизацией (по времени и по уровню). Есть две основные характеристики цифрового сигнала — частота дискретизации и глубина дискретизации по уровню.
Частота дискретизации указывает на то, с какими интервалами по времени идут данные об уровне сигнала. Существует теорема Котельникова (в западной литературе её упоминают как теорему Найквиста — Шеннона, хотя встречается и название Котельникова — Шеннона), которая утверждает: для возможности точного восстановления аналогового сигнала из дискретного требуется, чтобы частота дискретизации была минимум в два раза выше, чем максимальная частота в аналоговом сигнале. Если брать примерный диапазон воспринимаемых человеком частот звука 20 Гц — 20 кГц, то оптимальная частота дискретизации (частота Найквиста) должна быть в районе 40 кГц. У стандартных аудио-CD она составляет 44.1 кГц
Глубина дискретизации по уровню описывает разрядность числа, которым описывается уровень сигнала. Эта характеристика накладывает ограничение на точность записи уровня сигнала и на его минимальное значение. Стоит специально отметить, что данная характеристика не имеет отношения к громкости — она отражает точность записи сигнала. Стандартная глубина дискретизации на audio-CD — 16 бит. При этом, если не использовать специальную студийную аппаратуру, разницу в звучании большинство перестаёт замечать уже в районе 10-12 бит. Однако большая глубина дискретизации позволяет избежать появления шумов при дальнейшей обработке звука.
В цифровом звуке можно выделить три основных источника шумов.
Джиттер
Шум дробления
Он напрямую связан с глубиной дискретизации. Так как при оцифровке сигнала его реальные значения округляются с определённой точностью, возникают слабые шумы, связанные с её потерей. Эти шумы могут появляться не только на стадии оцифровки, но и в процессе цифровой обработки (например, если сначала уровень сигнала сильно понижается, а затем — снова повышается).
Алиасинг
При оцифровке возможна ситуация, при которой в цифровом сигнале могут появиться частотные составляющие, которых не было в оригинальном сигнале. Данная ошибка получила название Aliasing. Этот эффект напрямую связан с частотой дискретизации, а точнее — с частотой Найквиста. Проще всего понять, как это происходит, рассмотрев вот эту картинку:
Зелёным показана частотная составляющая, частота которой выше частоты Найквиста. При оцифровке такой частотной составляющей не удаётся записать достаточно данных для её корректного описания. В результате при воспроизведении получается совершенно другой сигнал — жёлтая кривая.
Для начала стоит сразу понять, что когда речь идёт о цифровом сигнале, то можно говорить только об относительном уровне сигнала. Абсолютный зависит в первую очередь от воспроизводящей аппаратуры и прямо пропорционален относительному. При расчётах относительных уровней сигнала принято использовать децибелы. При этом за точку отсчёта берётся сигнал с максимально возможной амплитудой при заданной глубине дискретизации. Этот уровень указывается как 0 dBFS (dB — децибел, FS = Full Scale — полная шкала). Более низкие уровни сигнала указываются как -1 dBFS, -2 dBFS и т.д. Вполне очевидно, что более высоких уровней просто не бывает (мы изначально берём максимально возможный уровень).
Поначалу бывает тяжело разобраться с тем, как соотносятся децибелы и реальный уровень сигнала. На самом деле всё просто. Каждые ~6 dB (точнее 20 log(2) ~ 6.02 dB) указывают на изменение уровня сигнала в два раза. То есть, когда мы говорим о сигнале с уровнем -12 dBFS, понимаем, что это сигнал, уровень которого в четыре раза меньше максимального, а -18 dBFS — в восемь, и так далее. Если посмотреть на определение децибела, в нём указывается значение — тогда откуда берётся 20? Всё дело в том, что децибел — это логарифм отношения двух одноимённых энергетических величин, умноженный на 10. Амплитуда же не является энергетической величиной, следовательно её нужно перевести в подходящую величину. Мощность, которую переносят волны с разными амплитудами, пропорциональна квадрату амплитуды. Следовательно для амплитуды (если все прочие условия, кроме амплитуды принять неизменными) формулу можно записать как
N.B. Стоит упомянуть, что логарифм в данном случае берётся десятичный, в то время как большинство библиотек под функцией с названием log подразумевает натуральный логарифм.
При различной глубине дискретизации уровень сигнала по этой шкале изменяться не будет. Сигнал с уровнем -6 dBFS останется сигналом с уровнем -6 dBFS. Но всё же одна характеристика изменится — динамический диапазон. Динамический диапазон сигнала — это разница между его минимальным и максимальным значением. Он рассчитывается по формуле , где n — глубина дискретизации (для грубых оценок можно пользоваться более простой формулой: n * 6). Для 16 бит это ~96.33 dB, для 24 бит ~144.49 dB. Это означает, что самый большой перепад уровня, который можно описать с 24-битной глубиной дискретизации (144.49 dB), на 48.16 dB больше, чем самый большой перепад уровня с 16-битной глубиной (96.33 dB). Плюс к тому — шум дробления при 24 битах на 48 dB тише.
Когда мы говорим о восприятии звука человеком, следует сначала разобраться, каким образом люди воспринимают звук. Очевидно, что мы слышим с помощью ушей. Звуковые волны взаимодействуют с барабанной перепонкой, смещая её. Вибрации передаются во внутреннее ухо, где их улавливают рецепторы. То, насколько смещается барабанная перепонка, зависит от такой характеристики, как звуковое давление. При этом воспринимаемая громкость зависит от звукового давления не напрямую, а логарифмически. Поэтому при изменении громкости принято использовать относительную шкалу SPL (уровень звукового давления), значения которой указываются всё в тех же децибелах. Стоит также заметить, что воспринимаемая громкость звука зависит не только от уровня звукового давления, но ещё и от частоты звука:
Простейшим примером обработки звука является изменение его громкости. При этом происходит просто умножение уровня сигнала на некоторое фиксированное значение. Однако даже в таком простом деле, как регулировка громкости, есть один подводный камень. Как я уже отметил ранее, воспринимаемая громкость зависит от логарифма звукового давления, а это значит, что использование линейной шкалы громкости оказывается не очень эффективным. При линейной шкале громкости возникает сразу две проблемы — для ощутимого изменения громкости, когда ползунок находится выше середины шкалы приходится достаточно далеко его сдвигать, при этом ближе к самому низу шкалы сдвиг меньше, чем на толщину волоса, может изменить громкость в два раза (думаю, с этим каждый сталкивался). Для решения данной проблемы используется логарифмическая шкала громкости. При этом на всей её длине передвижение ползунка на фиксированное расстояние меняет громкость в одинаковое количество раз. В профессиональной записывающей и обрабатывающей аппаратуре, как правило, используется именно логарифмическая шкала громкости.
Тут я, пожалуй, немного вернусь к математике, потому что реализация логарифмической шкалы оказывается не такой простой и очевидной вещью для многих, а найти в интернете данную формулу не так просто, как хотелось бы. Заодно покажу, как просто переводить значения громкости в dBFS и обратно. Для дальнейших объяснений это будет полезным.
- точность, с которой указывается уровень сигнала, ограничена (причём достаточно сильно. 16 бит — это в 2 раза меньше, чем используется для стандартного числа с плавающей точкой);
- у сигнала есть верхняя граница уровня, за которую он не может выйти.
- уровень шумов дробления возрастает при увеличении громкости. Для малых изменений обычно это не очень критично, так как изначальный уровень шума значительно тише ощутимого, и его можно безопасно поднимать в 4-8 раз (например, применять эквалайзер с ограничением шкалы в ±12dB);
- не стоит сначала сильно понижать уровень сигнала, а затем сильно его повышать — при этом могут появиться новые шумы дробления, которых изначально не было.
На практике всё это означает, что стандартные для Audio-CD параметры дискретизации (16 бит, 44,1 кГц) не позволяют производить качественную обработку звука, потому что имеют очень малую избыточность. Для этих целей лучше использовать более избыточные форматы. Однако стоит учитывать, что общий размер файла пропорционален параметрам дискретизации, поэтому выдача таких файлов для он-лайн воспроизведения — не лучшая идея.
Для того чтобы сравнивать громкость двух разных сигналов, её для начала нужно как-то измерить. Существует по меньшей мере три метрики для измерения громкости сигналов — максимальное пиковое значение, усреднённое значение уровня сигнала и метрика ReplayGain.
Усреднённое значение уровня сигнала — более полезная метрика и легко вычислимая, но всё же имеет существенные недостатки, связанные с тем, как мы воспринимаем звук. Визг циркулярной пилы и рокот водопада, записанные с одинаковым средним уровнем сигнала, будут восприниматься совершенно по-разному.
ReplayGain наиболее точно передает воспринимаемый уровень громкости записи и учитывает физиологические и психические особенности восприятия звука. Для промышленного выпуска записей многие звукозаписывающие студии используют именно её, также она поддерживается большинством популярных медиа-плееров. (Русская статья на WIKI содержит много неточностей и фактически не корректно описывает саму суть технологии)
Если мы можем измерять громкость различных записей, мы можем её нормализовать. Идея нормализации состоит в том, чтобы привести разные звуки к одинаковому уровню воспринимаемой громкости. Для этого используется несколько различных подходов. Как правило, громкость стараются максимизировать, но это не всегда возможно из-за ограничений максимального уровня сигнала. Поэтому обычно берётся некоторое значение немного меньше максимума (например -14 dBFS), к которому пытаются привести все сигналы.
Иногда нормализацию громкости производят в рамках одной записи — при этом различные части записи усиливают на разные величины, чтобы их воспринимаемая громкость была одинаковой. Такой подход очень часто применяется в компьютерных видео-плеерах — звуковая дорожка многих фильмов может содержать участки с очень сильно отличающейся громкостью. В такой ситуации возникают проблемы при просмотре фильмов без наушников в позднее время — при громкости, на которой нормально слышен шёпот главных героев, выстрелы способны перебудить соседей. А на громкости, при которой выстрелы не бьют по ушам, шёпот становится вообще неразличим. При внутри-трековой нормализации громкости плеер автоматически увеличивает громкость на тихих участках и понижает на громких. Однако этот подход создаёт ощутимые артефакты воспроизведения при резких переходах между тихим и громким звуком, а также порой завышает громкость некоторых звуков, которые по задумке должны быть фоновыми и еле различимыми.
Я не стану описывать совсем все аудио-фильтры, ограничусь только стандартными, которые присутствуют в Web Audio API. Самым простым и распространённым из них является биквадратный фильтр (BiquadFilterNode) — это активный фильтр второго порядка с бесконечной импульсной характеристикой, который может воспроизводить достаточно большое количество эффектов. Принцип работы этого фильтра основан на использовании двух буферов, каждый с двумя отсчётами. Один буфер содержит два последних отсчёта во входном сигнале, другой — два последних отсчёта в выходном сигнале. Результирующее значение получается с помощью суммирования пяти значений: текущего отсчёта и отсчётов из обоих буферов перемноженных на заранее вычисленные коэффициенты. Коэффициенты данного фильтра задаются не напрямую, а вычисляются из параметров частоты, добротности (Q) и усиления.
Все графики ниже отображают диапазон частот от 20 Гц до 20000 Гц. Горизонтальная ось отображает частоту, по ней применяется логарифмический масштаб, вертикальная — магнитуду (жёлтый график) от 0 до 2, или фазовый сдвиг (зелёный график) от -Pi до Pi. Частота всех фильтров (632 Гц) отмечена красной чертой на графике.
Lowpass

Рис. 8. Фильтр lowpass.
Пропускает только частоты ниже заданной частоты. Фильтр задаётся частотой и добротностью.
Highpass

Рис. 9. Фильтр highpass.
Действует аналогично lowpass, за исключением того, что он пропускает частоты выше заданной, а не ниже.
Bandpass

Рис. 10. Фильтр bandpass.
Этот фильтр более избирателен — он пропускает только определённую полосу частот.
Notch

Рис. 11. Фильтр notch.
Является противоположностью bandpass — пропускает все частоты вне заданной полосы. Стоит, однако, отметить разность в графиках затухания воздействия и в фазовых характеристиках данных фильтров.
Lowshelf

Рис. 12. Фильтр lowshelf.
Highshelf

Рис. 13. Фильтр highshelf.
Более умная версия lowpass — усиливает или ослабляет частоты выше заданной, частоты ниже пропускает без изменений.
Peaking

Рис. 14. Фильтр peaking.
Фильтр allpass

Рис. 15. Фильтр allpass.
Allpass отличается ото всех остальных — он не меняет амплитудные характеристики сигнала, вместо чего делает фазовый сдвиг заданных частот. Фильтр задаётся частотой и добротностью.
Фильтр WaveShaperNode
Фильтр ConvolverNode
Для работы данного фильтра требуется разложение сигнала на частотные составляющие. Это разложение производится с помощью быстрого преобразования Фурье (к сожалению, в русскоязычной Википедии совершенно несодержательная статья, написанная, судя по всему, для людей, которые и так знают, что такое БПФ и сами могут написать такую же несодержательную статью). Как я уже говорил во вступлении, не стану приводить в данной статье математику БПФ, однако не упомянуть краеугольный алгоритм для цифровой обработки сигналов было бы неправильно.
Данный фильтр реализует эффект реверберации. Существует множество библиотек готовых аудио-буферов для данного фильтра, которые реализуют различные эффекты (1, 2), подобные библиотеки хорошо находятся по запросу [impulse response mp3].
Большое спасибо моим коллегам, которые помогали собирать материалы для этой статьи и давали полезные советы.
Отдельное спасибо Тарасу Audiophile Ковриженко за описание алгоритмов нормализации и максимизации громкости и Сергею forgotten Константинову за большое количество пояснений и советов по данной статье.
UPD. Поправил раздел про фильтрацию и добавил ссылки по разным типам фильтров. Спасибо Денису deniskreshikhin Крешихину и Никите merlin-vrn Киприянову за то, что обратили внимание.

Автозвук
Далее будет рассмотрена теория звука и акустики с точки зрения физики. В данном случае я постараюсь сделать это максимально доступно для понимания любого человека, который, возможно, далёк от знания физических законов или формул, но тем не менее страстно грезит воплощением мечты создания совершенной акустической системы. Я не берусь утверждать, что для достижения хороших результатов в этой области в домашних условиях (или в автомобиле, например) необходимо знать эти теории досканально, однако понимание основ позволит избежать множество глупых и абсурдных ошибок, а так же позволит достичь максимального эффекта звучания от системы любого уровня.

Человеческое ухо устроено таким образом, что способно воспринимать волны только в ограниченном диапазоне, примерно 20 Гц — 20000 Гц (зависит от особенностей конкретного человека, кто-то способен слышать чуть больше, кто-то меньше). Таким образом, это не означает, что звуков ниже или выше этих частот не существует, просто человеческим ухом они не воспринимаются, выходя за границу слышимого диапазона. Звук выше слышимого диапазона называется ультразвуком, звук ниже слышимого диапазона называется инфразвуком. Некоторые животные способны воспринимать ультра и инфра звуки, некоторые даже используют этот диапазон для ориентирования в пространстве (летучие мыши, дельфины). В случае, если звук проходит через среду, которая напрямую не соприкасается с органом слуха человека, то такой звук может быть не слышим или сильно ослабленным в последствии.
В музыкальной терминологии звука существуют такие важные обозначения, как октава, тон и обертон звука. Октава означает интервал, в котором соотношение частот между звуками составляет 1 к 2. Октава обычно очень хорошо различима на слух, в то время как звуки в пределах этого интервала могут быть очень похожими друг на друга. Октавой также можно назвать звук, который делает вдвое больше колебаний, чем другой звук, в одинаковый временной период. Например, частота 800 Гц, есть ни что иное, как более высокая октава 400 Гц, а частота 400 Гц в свою очередь является следующей октавой звука частотой 200 Гц. Октава в свою очередь состоит из тонов и обертонов. Переменные колебания в гармонической звуковой волне одной частоты воспринимаются человеческим ухом как музыкальный тон. Колебания высокой частоты можно интерпретировать как звуки высокого тона, колебания низкой частоты – как звуки низкого тона. Человеческое ухо способно чётко отличать звуки с разницей в один тон (в диапазоне до 4000 Гц). Несмотря на это, в музыке используется крайне малое число тонов. Объясняется это из соображений принципа гармонической созвучности, всё основано на принципе октав.
В теории звука также присутствует такое понятие как ШУМ. Шум — это любой звук, которой создаётся совокупностью несогласованных между собой источников. Всем хорошо знаком шум листвы деревьев, колышимой ветром и т.д.
От чего зависит громкость звука? Очевидно, что подобное явление напрямую зависит от количества энергии, переносимой звуковой волной. Для определения количественных показателей громкости, существует понятие — интенсивность звука. Интенсивность звука определяется как поток энергии, прошедший через какую-то площадь пространства (например, см2) за единицу времени (например, за секунду). При обычном разговоре интенсивность составляет примерно 9 или 10 Вт/см2. Человеческое ухо способно воспринимать звуки достаточно широкого диапазона чувствительности, при этом восприимчивость частот неоднородна в пределах звукового спектра. Так наилучшим образом воспринимается диапазон частот 1000 Гц — 4000 Гц, который наиболее широко охватывает человеческую речь.
Волновая природа звука
Скорость звука
В жидкой и твёрдой средах принцип распространения и скорость звука аналогичны тому, как волна распространяется в воздухе: путём сжатия-разряжения. Но в данных средах, помимо той же зависимости от температуры, достаточно важное значение имеет плотность среды и её состав/структура. Чем меньше плотность вещества, тем скорость звука выше и наоборот. Зависимость же от состава среды сложнее и определяется в каждом конкретном случае с учётом расположения и взаимодействия молекул/атомов.
Скорость звука в воздухе при t, °C 20: 343 м/с
Скорость звука в дистиллированной воде при t, °C 20: 1481 м/с
Скорость звука в стали при t, °C 20: 5000 м/с
Стоячие волны и интерференция
Явление резонанса
Частотный спектр звука и АЧХ
Распространение звуковых волн, фаза и противофаза
Самым доступным образом можно описать это явление так: два сигнала с одинаковыми колебаниями (частотой), но сдвинутые по времени. Ввиду этого, удобнее представить эти явления смещения на примере обычных круглых стрелочных часов. Представим, что на стене висит несколько одинаковых круглых часов. Когда секундные стрелки этих часов бегут синхронно, на одних часах 30 секунд и на других 30, то это пример сигнала, который находится в фазе. Если же секундные стрелки бегут со смещением, но скорость по-прежнему одинакова, например, на одних часах 30 секунд, а на других 24 секунды, то это и есть классический пример смещения (сдвига) по фазе. Таким же образом фаза измеряется в градусах, в пределах виртуальной окружности. В этом случае, при смещении сигналов относительно друг друга на 180 градусов (половина периода), и получается классическая противофаза. Нередко на практике возникают незначительные смещения по фазе, которые так же можно определить в градусах и успешно устранить.
В процессе распространения звуковых волн в пространстве неизбежно происходит снижение их интенсивности, можно сказать затухание волн и ослабление звука. На практике столкнуться с подобным эффектом достаточно просто: например, если два человека встанут в поле на некотором близком расстоянии (метр и ближе) и начнут что-то говорить друг другу. Если впоследствии увеличивать расстояние между людьми (если они начнут отдаляться друг от друга), тот же самый уровень разговорной громкости будет становиться всё менее и менее слышимым. Подобный пример наглядно демонстрирует явление снижения интенсивности звуковых волн. Почему это происходит? Причиной тому различные процессы теплообмена, молекулярного взаимодействия и внутреннего трения звуковых волн. Наиболее часто на практике происходит превращение звуковой энергии в тепловую. Подобные процессы неизбежно возникают в любой из 3-ёх сред распространения звука и их можно охарактеризовать как поглощение звуковых волн.
Интенсивность и степень поглощения звуковых волн зависит от многих факторов, таких как: давление и температура среды. Также поглощение зависит от конкретной частоты звука. При распространении звуковой волны в жидкостях или газах возникает эффект трения между разными частицами, которое называется вязкостью. В результате этого трения на молекулярном уровне и происходит процесс превращения волны из звуковой в тепловую. Другими словами, чем выше теплопроводность среды, тем меньше степень поглощения волн. Поглощение звука в газовых средах зависит ещё и от давления (атмосферное давление меняется с повышением высоты относительно уровня моря). Что касательно зависимости степени поглощения от частоты звука, то принимая во внимание вышеназванные зависимости вязкости и теплопроводности, поглощение звука тем выше, чем выше его частота. Для примера, при нормальной температуре и давлении, в воздухе поглощение волны частотой 5000 Гц составляет 3 Дб/км, а поглощение волны частотой 50000 Гц составит уже 300 Дб/м.
В твёрдых средах сохраняются все вышеназванные зависимости (теплопроводность и вязкость), однако к этому добавляется ещё несколько условий. Они связаны с молекулярной структурой твёрдых материалов, которая может быть разной, со своими неоднородностями. В зависимости от этого внутреннего твёрдого молекулярного строения, поглощение звуковых волн в данном случае может быть различным, и зависит от типа конкретного материала. При прохождении звука через твёрдое тело, волна претерпевает ряд преобразований и искажений, что чаще всего приводит к рассеиванию и поглощению звуковой энергии. На молекулярном уровне может возникнуть эффект дислокаций, когда звуковая волна вызывает смещение атомных плоскостей, которые затем возвращаются в исходное положение. Либо же, движение дислокаций приводит к столкновению с перпендикулярными им дислокациями или дефектами кристаллического строения, что вызывает их торможение и как следствие некоторое поглощение звуковой волны. Однако, звуковая волна может и резонировать с данными дефектами, что приведет к искажению исходной волны. Энергия звуковой волны в момент взаимодействия с элементами молекулярной структуры материала рассеивается в результате процессов внутреннего трения.
В следующей статье я постараюсь разобрать особенности слухового восприятия человека и некоторые тонкости и особенности распространения звука.
Соавтор(ы): Andrew Peters. Эндрю Питерс — специалист по архитектуре и строительству, глава предлагающей полный спектр услуг архитектурно-строительной фирмы Peters Design-Build в области залива Сан-Франциско. Имеет более 20 лет опыта, специализируется на устойчивых и холистических практиках проектирования и строительства. Получил диплом бакалавра по архитектуре, прошел сертификацию в качестве профессионала управления проектами (PMP) и является аккредитованным профессионалом энергоэффективного и экологического проектирования (LEED). Работал менеджером завоевавшего международное признание проекта Refract House, представленного командой Калифорнии на конкурс Solar Decathlon министерства энергетики США в 2009 году, который освещался в более чем 600 статьях в интернете и печати.
Количество источников, использованных в этой статье: 11. Вы найдете их список внизу страницы.
Читайте также:


