Как сделать числа фибоначчи в excel
Числа Фибоначчи — это числа такой последовательности, в которой первые два элемента — 0 и 1, а каждый последующий элемент равен сумме двух предшествующих. Выглядит это так:
Примечание Иногда 0 опускается, и в этом случае ряд начинается с 1, но мы будем использовать последовательность с 0 на первой позиции.
Формула записывается следующим образом:
Вычисление ряда Фибоначчи — стандартная задача, которую задают на собеседованиях, чтобы проверить кандидата на понимание алгоритмов. Не так популярна, как сортировка, но всё же.
Давайте вычислим ряд и его отдельные элементы, использовав для этого язык Java.
Вычислить ряд Фибоначчи циклом
Предположим, что нам нужно вывести на экран первые десять чисел последовательности Фибоначчи. Мы помним, что:
- первый элемент ряда — 0, второй — 1;
- каждый последующий — сумма двух предыдущих.
Тогда наша последовательность будет иметь такой вид:
Но нам нужно вывести результат с использованием программы. Держите код с объяснениями в комментариях:
Выполнение завершится на десятом элементе. Количество элементов при этом можно менять, изменив значение в условиях цикла.
Найти число Фибоначчи через рекурсию
Рекурсивная функция — это такая функция, которая вызывает саму себя. Она также неплохо отрабатывает в алгоритмических задачах вроде чисел Фибоначчи, но ей требуется больше времени.
Почему так происходит? Всё дело в том, что рекурсивная функция приводит к многоразовому вызову одних и тех же операций. Именно из-за этого её не рекомендуется использовать, но если уж на собеседовании прозвучит такая задача, вы будете готовы.
Рассмотрим пример, в котором нам нужно получить n-ое число в ряде Фибоначчи:
Если в качестве num задать большое значение, программа зависнет.
Тип int в Java может хранить значения до 2147483647, так что вычислить получится лишь первые 46 чисел Фибоначчи. Тип long хранит до 9223372036854775807, а это 91 число Фибоначчи. Класс BigInteger призван работать с действительно большими значениями, вот только само выполнение программы это никак не ускорит.
Использовать для вычисления Stream
Stream в Java — это компонент для самостоятельной внутренней итерации своих же элементов. Подробнее о нём вы можете почитать в нашей статье о Java Stream API.
И, разумеется, Stream подходит для вычисления элементов последовательности Фибоначчи:
В данном примере метод iterate() будет возвращать упорядоченный поток, ограниченный лимитом в num значений и созданный с применением функции к начальному массиву arr . В консоль будет выведено следующее:
А так мы получим сумму чисел последовательности по элемент num включительно:
Последовательность Фибоначчи u0, u1, … образуется по закону:
Числа Фибоначчи получили название в честь итальянского математика XIII века Леонардо Фибоначчи, который ввел их для описания численности поколений животных (без учета смертности). Предполагается, что каждая пара животных некоторого вида приносит ежегодно приплод в одну пару животных (самку и самца), которые в свою очередь начинают давать приплод через два года после рождения. Определить, сколько пар животных будет иметься по прошествии n лет (un+1).
· Создать процедуру с именем FBN для решения задачи Фибоначчи.
Выходные данные: U – количество пар животных (целое)
· Организовать ввод и вывод данных через диалоговые окна.
· При вводе неверных значений повторять ввод.
· Создать на пустом листе кнопку, вызывающую процедуру FBN.
1. Создайте новую рабочую книгу с листами Оглавление, Май, Июнь и Июль.
2. Откройте панель Элементы управления в меню Вид, Панели инструментов.
3. С помощью кнопки создайте на рабочем листе Оглавление три КНОПКИ. По умолчанию создаваемые кнопки имеют имена Кнопка 1, Кнопка 2 и Кнопка 3, которые выводятся в поле имен и на поверхности кнопок.
4. Щелкнув правой кнопкой мыши кнопку с именем Кнопка1 выберите из меню Объект, Кнопка, Редактировать и исправьте надпись с Кнопка 1 на Май. Эта операция изменяет только надпись, но не имя кнопки (оно будет прежним, и именно оно будет выводиться в поле имен).
5. Замените имена у двух оставшихся кнопок на Июнь и Июль соответственно.
6. Дважды щелкнув левой кнопкой мыши на кнопку Май, раскройте редактор VBA и введите текст событийной процедуры Click объекта CommandButton:
Private Sub CommandButton1_Click()
‘ активировать лист Май
7. Повторите эти действия для кнопок Июнь и Июль, введя для каждой следующие процедуры:
Private Sub CommandButton2_Click()
Private Sub CommandButton3_Click()
В этих процедурах использовался метод Activate. Это метод активизирует объект, в данном случае — рабочий лист Sheets.
Для создания диалоговых окон, разрабатываемых приложений в VBA, используются формы. Редактор форм является одним из основных инструментов визуального программирования. Форма в проект добавляется с помощью команды Вставка, Форма (Insert, Form) или нажатием кнопки Вставить UserForm (Insert UserForm). В результате на экран выводится незаполненная форма с панелью инструментов Панель элементов (Toolbox)
Используя панель инструментов Панель элементов из незаполненной формы, можно сконструировать любое требуемое для приложения диалоговое окно.
2. Создайте кнопку Ввод данных через форму.
3. Теперь нужно создать форму для ввода данных:
4. Запустите редактор VBA и добавьте форму, выполнив команду Вставка, Форма (Insert, User Form).Откроется окно дизайнера форм Form designer, в котором будет представлено пустое серое окно формы (по умолчанию она будет называться UserForm1) и рядом — Toolbox, панель с набором элементов управления.
5. Теперь на этой форме нужно разместить все нужные нам элементы управления:
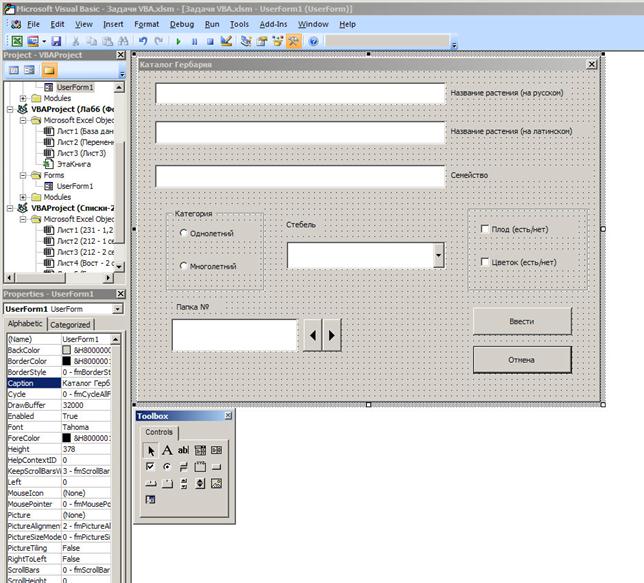
6. После того, как форма создана, приступаем к написанию процедур обработки событий. Двойной щелчок левой кнопкой мыши на самой форме и любом из объектов формы, раскрывает окно редактора VBA. Здесь можно писать процедуры обработки событий для любого из объектов.
7. При вызове (активизации) формы должны быть заданы начальные значения для всех полей. Поэтому нужно описать событийную процедуру Activate для нашей формы, в которой зададим все исходные значения:
Занятие 16. Построение динамических моделей в Excel. Моделирование одновременного действия температуры, влажности и тяжелых металлов на распределение растений по участкам территории при помощи электронной таблицы Excel.
Пусть на Листе0, Листе1, Листе2, Листе3 заданы известные распределения абиотических показателей (температура - таблицы 1, влажность - таблицы 2, тяжелые металлы - таблицы 3) на различных территориях.
Также известна степень влияния этих факторов на урожайность (таблица 5).
Как написать иструкцию на языке Visual Basic for Application(VBA)-язык макросов в MS Excel,чтобы вывести в таблицу числа Фибоначчи, хотя бы до 60 члена последовательности??
Sub ppp1()
Ë = 60
kk = 1
ff1 = 1
ff2 = 1
For ii = 3 To Ë
ff = ff2 + ff1
ff1 = ff2
ff2 = ff
Cells(kk, 1) = ff
kk=kk+1
Next ii
End Sub
Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.

Занимаясь изучением обработки данных, расчётами, а также другими компьютерными и математическими операциями, мы сталкиваемся со многими алгоритмами. Несмотря на то, что иногда мы недолюбливаем математику, мы зачастую даже не подозреваем, что окружены великим множеством вещей, идеально сбалансированных по ее принципам самой природой.
Одним из таких принципов, который весьма интересен для изучения, является последовательность Фибоначчи. Мы можем обнаружить ее во многих проявлениях природы: в числе лепестков цветка, количестве спиралей у подсолнуха и т.д.

В процессе работы с кодом мы сталкиваемся со многими алгоритмами: рекурсивные, типа “разделяй и властвуй”, рандомизированные, методы подбора и пр. Однако одними из наиболее полезных являются именно рекурсивные алгоритмы.

В первую очередь, алгоритм является набором задач, которым необходимо следовать для решения проблемы. Время его выполнения определяется числом шагов, необходимых для завершения всех этих задач (в некоторых случаях термин runtime может обозначать нотацию О большое в CS, которая описывает качество алгоритма).
Так что же такое рекурсия и как работает рекурсивная функция?

Рекурсия — это процесс, при котором некий элемент вызывает сам себя или описывает себя в виде ссылки на самого себя до выполнения некоего условия (true), затем этот процесс останавливается.
Рекурсивная функция — это функция, вызывающая саму себя в процессе выполнения, что также именуется как прямая рекурсия. В обратном смысле это выглядит как две функции, вызывающие друг друга, и называется непрямой рекурсией.
Для тех, кто только начал осваивать программирование будет очень полезным знать, как и когда стоит применять рекурсию или итеративные функции.
Математикам же последовательность Фибоначчи помогает мыслить более критически и развивать логику, работая с дифференциальными уравнениями.
Математическая формула Фибоначчи
Принцип построения последовательности Фибоначчи заключается в том, что каждое последующее ее число соответствует сумме двух ему предшествующих.
При n=0 мы получаем F0=0, а при n=1 получится F1=1. Нам всегда известны эти два начальных значения последовательности. Задача в том, чтобы выяснить, как формируются дальнейшие ее значения и каково будет значение для числа n, которое мы захотим проверить. Поэтому мы всегда начинаем с числа n>1.
Последовательность Фибоначчи рассчитывается по формуле, приведенной ниже:

Шаги вычисления значения Фибоначчи для n=6 :
А что получится, если мы возведем эти числа в квадрат?
В результате мы получим уже не числа Фибоначчи. Тем не менее они раскрываются внутри значений, получаемых при сложении этих чисел. Из этого можно сделать вывод, что почти каждая сумма является частью последовательности Фибоначчи. Давайте посмотрим, как работают числа Фибоначчи на примере золотого прямоугольника:

Нам всем известно, что:
Площадь прямоугольника S = b x h => b ширина, h высота.
Что же получится, если мы сложим квадраты чисел, как указано выше?
Площадь прямоугольника S = 1*1+ 1*1 + 2*2 +3*3 +5*5 + 8*8+13*13 = 273 = 13x21
И снова мы получаем числа Фибоначчи.
Если же поделить большее число последовательности на меньшее, то получатся, например, такие результаты:
13/8=1.625, 21/13=1.615, 34/21=1.619, 55/34=1.6176, 89/55=1.61818 …
Здесь мы видим значение, приближенное к значению золотого сечения, и чем большее число мы делим, тем больше их соответствие.
Ниже приведен JavaScript код, вычисляющий последовательность Фибоначчи. Временная сложность в нем линейна, т.к. цикл осуществляется от 2 до n. Время выполнения составляет О(n).
Читайте также:


