Как известно современные компьютеры работают с бинарной логикой
Люди выросли, считая от одного до 10, в десятичной системе, и все же мы все знаем, что современные компьютеры работают в двоичной системе Но знаете ли вы, почему это так? Почему не десятичная дробь или даже шестнадцатеричный система используется вместо? В этой статье мы все объясним.
Все основные системы нумерации мы используем являются «позиционными» в том смысле, что значение числа определяется местом его размещения. Мы называем это значением места (единицы, десятки, сотни . ), и оно помогает определить величину числа. Например, десятичная система, с которой мы все наиболее знакомы, показывает, сколько стоит «2» для позиции, в которой она находится, поскольку 2 не равно 20, как 200.
Значение чисел
Но это не всегда так. Этот способ представления значений является относительно современным и требует использования нулей в качестве заполнителей. Вот почему старые системы счисления, такие как римские цифры или египетские иероглифы не используют это значение места, но добавляют все цифры, чтобы получить общее значение.
Используя эту базовую концепцию стоимости места, мы создали различные системы нумерации или способы записи чисел. Они названы по количеству приращений на место, то есть во сколько раз вы можете увеличить значение одного места, прежде чем вам придется «переместить» его в следующее. Например, на десятичной основе мы можем увеличить число единиц в девять раз с 10 различными цифрами (считая ноль), прежде чем перейти от единиц к десяткам.
Почему ПК используют бинарную систему
Когда мы были детьми, нас учили считать по пальцам: десять пальцев, десять цифр. Чтобы сосчитать больше десяти, вы держали палец закрытым, пока подсчитывали остальные, и это базовая 10 или десятичная система, система, которую мы используем каждый день практически для всего.
Однако ПК не могут использовать базу 10, так как аппаратное обеспечение, в котором мы нуждаемся, было бы ужасно сложным , По этой причине ПК использовать двоичную систему (или основание два), которое имеет только два значения (единицы и нули) для подсчета, поскольку, как вы знаете, процессоры сделаны с транзисторами внутри это не что иное, как маленькие переключатели, которые пропускают или не пропускают электричество, тем самым представляя соответственно единицы и нули.
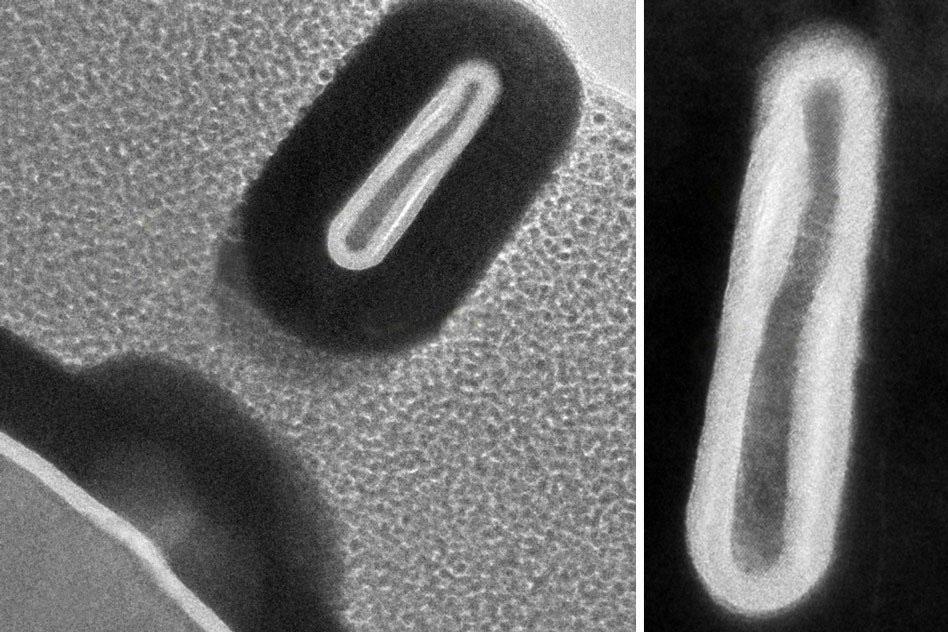
Другими словами, ПК не способны считать в десятичном или шестнадцатеричном формате, поскольку их схемы могут представлять только два состояния: включено и выключено, включено и выключено, единицы и нули. Поэтому наиболее естественным является то, что его «язык» является двоичным, состоящим из единиц и нулей, и буквально каждый бит данных, которыми управляет ПК, представляет собой не что иное, как последовательность единиц и нулей.
Многие скажут, что ПК также управляют данными в шестнадцатеричный системе, и это действительно случай, который немного край. Он используется как средство представления двоичных значений для понимания людьми: однозначное значение в шестнадцатеричном формате представляет четыре бита памяти, два разряда - восемь бит или один байт.
Вот почему вы увидите, что шестнадцатеричный используется для представления значения регистров памяти , поскольку его легче читать, чем большие строки из нулей и единиц, но в нижней части они все еще являются двоичными данными.

Конечно, было бы наиболее удобно, если бы мы могли использовать единую систему нумерации для всего, но, к сожалению, каждая система нумерации имеет свое собственное назначение, поэтому мы обречены использовать более одного, а в случае компьютеров это двоичный файл.
Однажды я прочитал в интернете про троичную систему счисления и заинтересовался. Меня мучил вопрос, а нельзя использовать в основе компьютера симметричную троичную систему счисления (СС), и даже вдруг это увеличит производительность компьютера? Мне казалось, что это возможно, и я жаждал это проверить.
Информация:
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3. Существует в двух вариантах: несимметричная и симметричная.
В несимметричной троичной системе счисления чаще применяются цифры , а в симметричной троичной системе счисления знаки , .
У некоторых людей эта логика вызывает затруднения. Они говорят, например, приведите пример подобной логики в жизни.
Человек, немного подумавший над этой логикой поймет, что она более жизненна чем двоичная. Обычный пример троичной логики в жизни связан с постоянным током: ток движется в одну сторону, в другую сторону, его нет.
Оказалось, что симметричная троичная система счисления использовалась давным-давно для решения «задачи о гирях», использовалась в компьютере Сетунь, построенном в 50-е годы в МГУ. С 2008 года в университете « California Polytechnic State University of San Luis Obispo» функционирует цифровая компьютерная система TCA2, основанная на троичной системе счисления.
В чем же плюсы троичной СС над двоичной? Рассмотрим эти плюсы:
Меньше разрядов
(Написано разжевано, чтобы каждый смог понять суть этого пункта)Возьмем число 10 в десятичной СС и переведем его в двоичную СС, получим 1010, переведем в троичную симметричную СС, получим +0+, ну а если в троичную несимметричную СС, то получим 101. Из этого мы видим, что в некоторых числах в троичной симметричной и несимметричной СС-ах меньше разрядов, чем в двоичной СС.
Возьмем число 5 в десятичной СС и переведем его в двоичную СС, получим 101, переведем в троичную симметричную СС, то получим +--, ну а если в троичную несимметричную СС, то получим 12. Из этого мы видим, что в некоторых числах в троичной несимметричной СС меньше разрядов, чем в двоичной и троичной симметричной СС-ах.
Емкость
Троичная СС вмещает больший диапазон чисел, т.к. 3^n>2^n (где n-натуральное число). Например, если n=9, то 3^9=19683>2^9=512.
3.
Экономичность системы счисления
Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p.
Мы рассмотрели троичную арифметику, теперь затронем логику:
В чем же проблемы двоичной логики?
1.Мощности компьютера, основанного на двоичной логике, не всегда хватает. Приведем пример. Одна из наиболее сложных систем защиты – криптосистема RSA. Вскрытие шифра RSA с длиной ключа 1024 бита (такая длина часто используется в информационных системах) займет в лучшем случае — при проведении распределенных вычислений на тысячах мощных ПК — не менее пятнадцати лет, а к тому времени данная система шифровки перестанет быть востребованной.
Докажем математически какая система счисления будет наилучшей для максимальной мощности и емкости памяти. Для этого рассмотрим функцию f(p)=p^(n/p), в которой p – основание системы счисления, а n – количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел, которое при этом можно записать, будет равно pn/p
f(p)=p^(n/p)
Для того, чтобы определить максимальное значение функции, найдем ее производную:
ln f = ln p^(n/p)
ln f =n/p* ln p
. (Я не буду приводить здесь всю математику)
n*p^(n/p-2) никогда не будет равно 0 => (1 — ln p)=0, ln p = 1, p = e
e = 2,71, а ближайшее целое число к нему – это три.
Значит, в этом плане лучшая система с целочисленным основанием — троичная.
Самое вкусненькое — рассмотрим троичные логические операции:
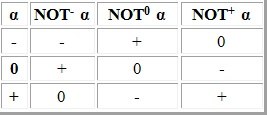
1.Отрицание

2.Конъюнкция — логическое И
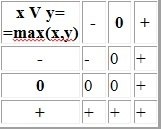
3.Дизъюнкция — логическое ИЛИ

4.Операция Выбора. Эта операция существует только для троичной логики. Таблица истинности каждой из этих трёх операций содержит везде „-“, кроме единственного значения, которое ею можно выбрать.
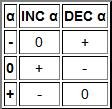
5.Модификация. Полное название этих одноместных операций: увеличение на единицу по модулю три (INC) и уменьшение на единицу по модулю три (DEC). Увеличение на единицу по модулю три – это циклическое прибавление единицы.
Здесь видны и прежде знакомые вам логические операции из двоичной логики, но добавились и новые…
Квантовые компьютеры
Итог:
В конечном итоге видно, что троичная симметричная система лучше двоичной системы в некоторых показателях, но не сильно выигрывает. Но с пришествием квантовых компьютеров троичные вычисления получили новую жизнь. Универсальные квантовые логические вентили — краеугольный камень новорожденных квантовых вычислительных систем — требует сотни вентилей для завершения одной полезной операции. Квантовый компьютер канадской компании D-Wave, анонсированный в прошлом году, состоит всего из 16 квантовых битов — кубитов — минимум, необходимый для управляемого вентиля «NOT». Использование в квантовом компьютере кутритов нужно было бы намного меньше вентилей для завершения одной операции. Я думаю, если бы началось производство и тестирование таких компьютеров, то результаты были бы лучше, чем у обычных компьютеров, вскоре началось бы массовое их производство, и про двоичные компьютеры все бы забыли…
Искусственный интеллект не защищен от ошибок. Ведь он — создание человеческого разума, а наше мышление — это скопище ошибок и заблуждений. Да, наши суждения часто ошибочны. Даже если мы очень стараемся судить объективно, мы всё равно обречены на стереотипное мышление и далеко идущие неаргументированные выводы. Однако ошибки ИИ вовсе не такие. Он ошибается не по причине субъективности, а из-за самой сути алгоритмического мышления. Во всём виновата бинарная логика.
Бинарная логика основана на двух утверждениях: истина (логическая единица ) или ложь (логический нуль ). Благодаря такому простому механизму возможно быстро и эффективно проводить вычисления. Чтобы машина могла понимать печатные символы и алфавит, используется кодировка ASCII (American Standard Code for Information Interchange). С ее помощью привычный человеку текст переводится в понятные машине нули и единицы.
Однако это не означает, что машина понимает мир и слова так же, как и мы. Нам приходится пользоваться бинарной логикой, чтобы общаться с машиной, но машина не может говорить с нами, пользуясь человеческими мыслительными процессами.

Мы не мыслим нулями, единицами и исключительно количественными категориями. Мы оперируем деталями, контекстами, разными измерениями, динамикой процессов, ценностями и богатством опыта.
Но самое интересное во всём этом, что бинарная логика — это вовсе не изобретение сумасшедших инженеров начала XX века. За бинарную логику стоит говорить спасибо Аристотелю.
Бинарная логика и сексизм Аристотеля
Что? Аристотелю? Отцу демократии и великому философу? За вот эту ущербную машинную логику?
Вообще да, именно ему и его теории дуализма. За 350 лет до нашей эры Аристотелю захотелось сделать мир проще и понятнее. За основу он взял пифагорейскую таблицу противоположностей, которая выглядела примерно так:
Конечность — бесконечность
Чёт — нечет
Единство — множество
Правый — левый
Покой — движение
Прямой — кривой
Добро — зло
и т. д.
Пифагор с помощью этой таблицы демонстрировал, что числа — это не про количество единиц, а про некую силу и вектор ее направления.
Аристотель посмотрел на нее и подумал: ведь разделение на противоположности работает и с людьми, и с животными, и с обществом. Кто-то занимает один полюс, а кто-то — другой. Кто-то прав, а кто-то виноват. Кто-то добр, а кто-то зол.
Аристотель соорудил на фундаменте дуализма иерархическую систему и снабдил ее собственными представлениями о носителях одной полярности (со значением «1») и другой (со значением «0»). Ну, к примеру:
1 = истина = разум = правый = мужчина
0 = ложь = чувства = левый = женщина
Вот такой сексизм 2000-летней давности.

Если бы Аристотель прислушивался к своим предшественникам, Сократу и Платону, он бы, возможно, не был бы так уверен в подчиненном положении женщин и ущербности их разума, и право голоса женщины получили бы не в начале XX века, а гораздо раньше.
В диалоге Платона «Пир» Сократ с большим уважением отзывался о мудрости жрицы Диотимы из Мантинеи, а в Книге 5 «Государства» он говорит, что управлять городом с равным успехом может и мужчина, и женщина.
Тем не менее именно аристотелевская логика легла в основу западной мысли и продолжает пускать ростки стереотипов и предубеждений.
Бинарная логика Декарта и китайская ошибка Лейбница
Эстафетную палочку Аристотеля перехватили в XVII–XVIII веках Декарт и Лейбниц. Декарт, изобретатель афоризма «Я мыслю, следовательно, я существую», зародил идею о том, что любой субъект имеет только ту ценность, которую ему приписывает наблюдатель.
Кроме того, рассуждения Декарта продолжали тенденцию отделения разума от телесных и чувственных проявлений: в «Размышлениях о первой философии» ученый отнес разум к миру идеального, а тела и чувства — к миру материального, где эти два мира не пересекаются.
Плюс Декарт был разочарован несистемными методами, которыми пользовались математики в его время и разработал дедуктивно-индуктивную логику, основы которой изложил в «Рассуждениях о познании». Математика в представлении Декарта должна иметь крепкий фундамент, и в качестве него он использовал аристотелевскую бинарную логику (1 = истина = действительно, 0 = ложь = недействительно), только упаковал ее в древовидную структуру. Теперь она используется в нейросетях при обработке естественных языков.
Немецкий мыслитель и юрист Лейбниц, создатель математического анализа (одновременно с Ньютоном), разработал бинарную модель счисления как быстрый способ получать готовые расчеты.
Интересно, что Лейбниц был ярым китаистом. В 1703 году священник Буве высылает мыслителю копию «Книги перемен» («И Цзин»), древний китайский философский текст. Книга состоит из 64 гексаграмм, в которых Лейбниц уловил сходство с собственными бинарными таблицами и пришел в восторг.
В одних гексаграммах Лейбниц увидел нули, а в других — единицы, что утвердило его в мысли о том, насколько бинарная логическая система универсальна и всеобъемлюща.

Вот только Лейбниц ошибся: во-первых, он рассматривал гексаграммы, перевернув их вверх ногами. Во-вторых, он не учел, что каждая гексаграмма соответствовала определенному описанию на китайском. В третьих, каждая из них представляла собой запись двух противоборствующих энергий — положительной и негативной, инь и ян.
В любом случае и Лейбниц, и Декарт сделали свой вклад в развитие западного мышления, замкнутого в противоестественной дуальной логике.
Бинарная логика сегодня
На бинарной логике построены все современные системы данных. Нулями и единицами пронизаны любые действия, которые производятся сегодня в цифровом поле. Вот, например:
Свайп вправо = 1, свайп влево = 0
Поставили лайк =1, не поставили = 0
Кажется, пользователь испытывает положительные эмоции = 1, отрицательные = 0
Группируем объекты по красному цвету: яблоко = 1, апельсин = 0
Машина лишь регистрирует, какой выбор сделал человек, и дает соответствующую реакцию, выбирая из двух вариантов.
Бинарная логика не предоставляет пространства для моделирования причин принятия подобных решений. Мы собираем черно-белые данные, сортируя их по оттенкам серого, когда мир вокруг — это целая радуга.
Окружающий нас мир не терпит бинарности. Частицы в квантовой суперпозиции могут быть одновременно и нулем, и единицей. Взаимосвязи между явлениями и свойствами богаче и неоднозначнее, чем чёт и нечет.
Бинарностью легко оперировать, но в таком случае нам стоит смириться с тем, что искусственный интеллект так и останется усовершенствованной моделью калькулятора.

Компьютеры не понимают слов и цифр так, как это делают люди. Современное программное обеспечение позволяет конечному пользователю игнорировать это, но на самых низких уровнях ваш компьютер оперирует двоичным электрическим сигналом, который имеет только два состояния: есть ток или нет тока. Чтобы «понять» сложные данные, ваш компьютер должен закодировать их в двоичном формате.
Двоичная система основывается на двух цифрах – 1 и 0, соответствующим состояниям включения и выключения, которые ваш компьютер может понять. Вероятно, вы знакомы с десятичной системой. Она использует десять цифр – от 0 до 9, а затем переходит к следующему порядку, чтобы сформировать двузначные числа, причем цифра из каждого следующего порядка в десять раз больше, чем предыдущая. Двоичная система аналогична, причем каждая цифра в два раза больше, чем предыдущая.
Подсчет в двоичном формате
В двоичном выражении первая цифра равноценна 1 из десятичной системы. Вторая цифра равна 2, третья – 4, четвертая – 8, и так далее – удваивается каждый раз. Добавление всех этих значений даст вам число в десятичном формате.
1111 (в двоичном формате) = 8 + 4 + 2 + 1 = 15 (в десятичной системе)
Учет 0 даёт нам 16 возможных значений для четырех двоичных битов. Переместитесь на 8 бит, и вы получите 256 возможных значений. Это занимает намного больше места для представления, поскольку четыре цифры в десятичной форме дают нам 10000 возможных значений. Конечно, бинарный код занимает больше места, но компьютеры понимают двоичные файлы намного лучше, чем десятичную систему. И для некоторых вещей, таких как логическая обработка, двоичный код лучше десятичного.
Следует сказать, что существует ещё одна базовая система, которая используется в программировании: шестнадцатеричная. Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют её для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры шестнадцатеричного числа могут представлять собой целый байт, то есть заменяют восемь цифр в двоичном формате. Шестнадцатеричная система использует цифры 0-9, а также буквы от A до F, чтобы получить дополнительные шесть цифр.
Почему компьютеры используют двоичные файлы
Короткий ответ: аппаратное обеспечение и законы физики. Каждый символ в вашем компьютере является электрическим сигналом, и в первые дни вычислений измерять электрические сигналы было намного сложнее. Было более разумно различать только «включенное» состояние, представленное отрицательным зарядом, и «выключенное» состояние, представленное положительным зарядом.
Для тех, кто не знает, почему «выключено» представлено положительным зарядом, это связано с тем, что электроны имеют отрицательный заряд, а больше электронов – больше тока с отрицательным зарядом.
Таким образом, ранние компьютеры размером с комнату использовали двоичные файлы для создания своих систем, и хотя они использовали более старое, более громоздкое оборудование, они работали на тех же фундаментальных принципах. Современные компьютеры используют, так называемый, транзистор для выполнения расчетов с двоичным кодом.
Вот схема типичного транзистора:

По сути, он позволяет току течь от источника к стоку, если в воротах есть ток. Это формирует двоичный ключ. Производители могут создавать эти транзисторы невероятно малыми – вплоть до 5 нанометров или размером с две нити ДНК. Это то, как работают современные процессоры, и даже они могут страдать от проблем с различением включенного и выключенного состояния (хотя это связано с их нереальным молекулярным размером, подверженным странностям квантовой механики).
Почему только двоичная система
Поэтому вы можете подумать: «Почему только 0 и 1? Почему бы не добавить ещё одну цифру?». Хотя отчасти это связано с традициями создания компьютеров, вместе с тем, добавление ещё одной цифры означало бы необходимость выделять ещё одно состояние тока, а не только «выключен» или «включен».
Проблема здесь в том, что если вы хотите использовать несколько уровней напряжения, вам нужен способ легко выполнять вычисления с ними, а современное аппаратное обеспечение, способное на это, не жизнеспособно как замена двоичных вычислений. Например, существует, так называемый, тройной компьютер, разработанный в 1950-х годах, но разработка на том и прекратилась. Тернарная логика более эффективна, чем двоичная, но пока ещё нет эффективной замены бинарного транзистора или, по крайней мере, нет транзистора столь же крошечных масштабов, что и двоичные.
Причина, по которой мы не можем использовать тройную логику, сводится к тому, как транзисторы соединяются в компьютере и как они используются для математических вычислений. Транзистор получает информацию на два входа, выполняет операцию и возвращает результат на один выход.
Таким образом, бинарная математика проще для компьютера, чем что-либо ещё. Двоичная логика легко преобразуется в двоичные системы, причем True и False соответствуют состояниям Вкл и Выкл .

Бинарная таблица истинности, работающая на двоичной логике, будет иметь четыре возможных выхода для каждой фундаментальной операции. Но, поскольку тройные ворота используют три входа, тройная таблица истинности имела бы 9 или более. В то время как бинарная система имеет 16 возможных операторов (2^2^2), троичная система имела бы 19683 (3^3^3). Масштабирование становится проблемой, поскольку, хотя троичность более эффективна, она также экспоненциально более сложна.
Кто знает? В будущем мы вполне возможно увидим тройничные компьютеры, поскольку бинарная логика столкнулась с проблемами миниатюризации. Пока же мир будет продолжать работать в двоичном режиме.
Я сделал некоторые поиски, но не нашел действительно удовлетворительного ответа. Как разработчик я хочу инвестировать необходимое время в понимание этого, поэтому я ищу полное объяснение по этому поводу и не стесняйтесь предоставлять любые полезные ссылки.
Я бы рекомендовал купить это книги by Эндрю С. Таненбаум. Он разработал один из предшественников Linux под названием Minix. Я использовал Архитектура Компьютера в рамках университетского курса.
Почему компьютеры используют двоичный файл, это не просто вопрос контекста коммутатора.
относительно опорного напряжения скажем 3v. +1v(4v) = true или 1 и-1v (2v) = false или 0.
Это связано с наиболее эффективный метод создания контролирующих или логических схем. Это связано со стоимостью осуществления. Сколько стоит построить схемы, которые работают с двоичными по сравнению с схемами, которые работают с десятичными или аналоговыми посмотреть этот ответ.
Если вы сравните, сколько миллиардов транзисторов двоичной схемы подходят для современного процессора. Стоимость этого с помощью десятичной (или аналоговой) системы увеличивается экспоненциально для каждой цифры, которую вы хотите добавить как теперь вы должны добавить, что гораздо больше контроля схемы.
Если вы хотите понять некоторые из наиболее важных компонентов, которые помогли сделать binary стандартом по умолчанию для логики и управления схемой, прочитайте и поймите следующие темы из Википедии. Это займет около 4 часов, чтобы прочитать наиболее важные темы, которые имеют отношение к некоторым из электротехники, используемой для создания схем.
Я пытался быть завершена в этот список понятий вам нужно понять, как работают фактические коммутаторы и почему они используются. А также почему Binary арифметика такая эффективная форма расчета в оборудовании.
теперь для некоторых жестких ядер. Си и C++ используется для написания драйверы устройств которые говорят с фактическим оборудованием. Если вы действительно хотите узнать, как работают определенные устройства, ваш процессор и / или внешний устройства изучать ассемблер. Вы начнете видеть, как вы можете отключить устройство, установив определенный регистр устройства на определенное значение, которое будет считываться логической схемой для изменения состояния устройств. Например, вы поймете, почему (0101) base2 = 5 (binary related stuff) будет направлять определенный путь через схемы для включения и выключения устройства.
компьютеры могли бы быть построены для работы даже с десятичными числами, но с инженерной точки зрения гораздо безопаснее различать только два состояния.
напряжение тока значения 1 (+5в) только теоретическое значение, в реальной жизни оно всегда отличает бит. Если бы они сделали компьютеры с десятичными дробями, невозможно было бы сказать, является ли +4.75 V 9 или 10.
Это потому, что как логические ворота работают: есть логический выход (1), Если управляющее напряжение превышает определенный порог; нет логического выхода (0), если нет.
но, вероятно, гораздо более важное:
возможно, однажды компьютеры больше не будут работать в двоичном формате, когда возникают квантовые машины (или другие подобные вещи, которые, возможно, будут поощрять более сложные представления состояний). но поскольку двоичные значения являются простейшим возможным представлением любого (более сложного) государство, даже в "квантовые времена", вероятно, было бы наиболее целесообразно остаться с компьютерами, работающими в двоичном формате (абстрагируясь от других физических представлений, таких как троичные или так, если дано).
компьютеры используют электричество как средство передачи информации. И самый простой способ использовать электричество в качестве информации в On или OFF (1 или 0).
конечно, вы можете использовать различное напряжение для представления другого числа, но электронные компоненты для этого действительно сложны.
также важно отметить, что способность писать и читать 1 и 0 достаточно для вычисления любого вычисления, это называется Тьюринг полнота, значит, есть нет необходимости искать более сложные системы, позволяющие что-то другое, чем binary
(хорошо, чтобы быть тщательным, полнота Тьюринга может быть достигнута только с бесконечной памятью, но это не очень актуально здесь.)
Ну, я думаю, вам нужно рассмотреть IC внутри ПК, каждый IC имеет миллионы ворот в основном NANDS или NORS, и каждое вычисление является либо истинным, либо ложным, т. е. 0 или 1 соответственно, и, таким образом, двоичное число будет достаточно. Надеюсь, это ясно : -)
Ok. Я дам вам свое мнение об этом, но сначала необходимо сказать, что я далек от того, чтобы быть экспертом, поэтому примите мой ответ осторожно.
в нижней части всего этого оборудования, ворот и транзисторов, компьютер это больше не схема. В каждой части цепи могут течь электрические импульсы. или не flow (это упрощенная версия, читайте комментарий paxdiablo). 2 государств. Эти два состояния могут быть представлены 0 или 1. И это бинарно!
на самом деле, математические расчеты могут быть сделаны в каждой базе, единственная причина, потому что человек использует base-10 заключается в том, что у нас (используется) есть 10 пальцев, поэтому нам легко понять. Цифровые системы имеют два состояния, поэтому base-2-лучший выбор для них.
Ну в компьютерах мы всегда идем с вещами с наименьшей сложностью, которая помогает нам ускорить вычисления. Поэтому здесь, если мы видим, что binary является наименее сложным из всех..
рассмотрим число 1000 здесь,
таким образом, мы видим, что binary имеет наименьшую сложность.
потому что компьютеры являются государственными машинами, и они понимают в основном два состояния. То есть, ВКЛ и ВЫКЛ, и это касается электричества. Это главная причина.
кроме того, как еще вы найдете футболки, говорящие, что есть 10 типов людей, тех, кто понимает двоичный и тех, кто этого не делает ? :)
компьютеры в основном работают с электрическими сигналами; как тупая машина, она может понимать только "высокий" и "низкий". Максимум +5v и низкий 0v. (V-вольт). Таким образом, 1 в двоичном формате представляет high или "on". 0 означает "низкий" или "off". Итак, двоичный файл необходим, чтобы компьютер что-то понял.
Читайте также:


