Ханойская башня своими руками
Это упражнение на развитие внимание мне особенно нравится. Его можно выполнять одному и уже через 10 минут мозг начинает дымиться от напряжения. Развивает концентрацию очень мощно.
Предыстория упражнения:
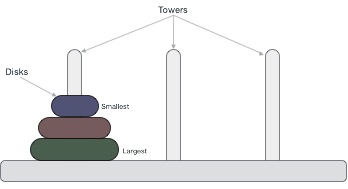
По официальной версии, Ханойские Башни —это головоломка, которую в 1883 г. придумал французский математик Эдуард Люка. Для тех, кто не знает, суть головоломки вот в чем: есть три стержня и восемь дисков разных диаметров, вначале все диски собраны на одном стержне так, что меньшие диски лежат на больших. Люка предлагал переложить все диски с первого стержня на третий, используя второй. При этом следует соблюдать следующее правило: диски можно перекладывать с одного стержня на другой, при этом нельзя класть диск поверх диска меньшего радиуса.
По той же официальной версии, ради повышения интереса к своей головоломке Люка придумал легенду, повествующую про башню Брамы, увеличенную копию Ханойской. Эта башня состояла то ли из 50, то ли из 64 золотых дисков, а стержни были вырезаны из алмаза. Так вот, башни Брамы были созданы не иначе как при Сотворении мира, и с того времени жрецы в храме трудятся, перекладывая диски. По имеющимся данным, как только они закончат, наступит конец света, и потому жрецы очень стараются… (Описание взял отсюда )
Игра забавная, но не более.
Гораздо интереснее выполнить упражнение не на компьютере, а в голове. И начать не с 8 дисков, а всего с трех.
Можно представить себе три стержня А, Б и В. Мне удобнее представлять три кубика.
На кубике В лежит 3 диска, самый большой внизу, маленький – наверху.
Напомню правила. За ход можно перемещать только верхние диски, класть всегда нужно меньший на больший. Цель игры – переместить пирамиду дисков с кубика В на кубик А, используя при игре все три кубика-площадки.
Пример алгоритма работы с тремя дисками, где 1 – самый маленький, а 3 – самый большой. Двигайте диски в следующем порядке.
1-Б, 2-А,1-А, 3-Б, 1-Б, 2-В, 1-В, 3-А, 1-Б,2-В,1-В
Каждое перемещение нужно себе четко представлять. В этой игре есть алгоритм последовательности, если вы его поймете – будет проще.
Когда наиграетесь с 3 дисками, переходите к четырем. Ну и так далее.
Через 10 минут с семью дисками у меня ощущение, что я несколько часов решал математические задачи.
Кстати, это упражнение шикарно развивает воображение, так что если у вас с представлением были сложности, Ханойская башня их решит.
Как опробуете игру, напишите – сколько дисков осилили, какие придумали фишки, чтобы было проще в голове все это крутить.
Высоко в горах Тибета монахи перекладывают 64 золотых диска, нанизанных на 3 алмазные стержня. Когда их работа будет окончена, наступит конец света.
Есть 3 стержня. На первый надеты n дисков увеличивающегося сверху вниз диаметра. Эти диски необходимо по одному переложить с первого стержня на второй. Можно использовать все стержни, но диски большего диаметра должны всегда находиться ниже дисков меньшего диаметра (на картинку можно кликать, а также менять число дисков: и стержней: )
В этом документе разбирается рекурсивное и нерекурсивные решения задачи, которую называют ханойской головоломкой. Будет написан класс Hanoi, умеющий рисовать башни (стержни с дисками), взаимодействовать с мышкой и самостоятельно принмать решения. В дальнейшем эта модель используется при обсуждении стратегий поиска в пространстве с большим числом состояний.
Рекурсивное решение
Пусть есть 3 башни (x, y, z) и, благодаря магическим способностям, мы умеем перекладывать n дисков с одной башни на другую. Применим эти способности, переложив n-1 дисков с x на z. Затем тривиальным образом перенесём оставшийся (самый большой) диск с x на y. Наконец, снова, применив магию, переложим n-1 дисков с z на y (поверх того, самого большого диска). Всё, задача по переносу n дисков с x на y решена, а её код на JavaScript имеет вид: Несмотря на ощущение надувательства, всё работает и вызов функции Hanoi1(3, "0", "1", "2") (башни нумеруем с нуля) приведёт к следующему результату (который стоит проверить, перекладывая диски мышкой):
.
Аналогичен алгоритм, на вход которого подаётся номер (по размеру) перкладываемого диска (их также нумеруем с нуля: d=0. n-1) и направление его сдвига s=1 (вправо) или s=-1 (влево). Сдвиг предполагается цикличным и при переносе с 0-го стрержня влево (s=-1) диск попадает на 2-й стержень, а при переносе со второго вправо (s=1) - попадает на 0-й. Пусть необходимо сдвинуть самый большой (нижний) диск (d=n-1) вправо (s=1). Для этого мы должны сдвинуть чуть меньший диск d-1 влево -s, затем переложить большой диск вправо, и затем на него положить меньший, снова сдвигая его влево (цикл через 3 тоже что 2 раза вправо): Этот, ещё более волшебный код, приводит к: , что означает: "перенести маленький диск под номером 0 вправо, затем следующий по размеру диск влево (окажется на последнем стержне), и т.д."
Разделяй и властвуй
Подсчитаем число ходов M(n,3)=Mn, которые необходимо сделать для решения задачи с n дисками и 3-мя башнями. Каждый вызов функции Hanoi1приводит к одному перекладыванию и двум выззовам с перекладыванием на единицу меньше. Поэтому справедливо рекурентное уравнение: Mn=1+2·Mn-1 с начальным условием M1=1. Прямой подстановкой несложно проверить, что ему удовлетворяет следующее решение: Mn = 2 n - 1.
Если натренированные монахи тратят секунду на один диск, то конца света следует ждать не ранее чем через 584 миллиарда лет (M64 = 2 64 - 1 = 1.8·10 19 секунд). Впрочем, когда они начали, нам неведомо.
Количество состояний системы (рассположений n дисков по t башням) вычисляется следующим образом. Первый диск может находиться на одной из t башень. Независимо от этого, второй диск, при каждой из t возможностей первого диска, также может находиться на t башнях, что даёт t·t возможностей и т.д.: N(n,t) = t n .
В таблице приведены значения функций Mn=M(n,3), Nn=N(n,3) и их отношение:
| n | 3 | 4 | 5 | 10 | 15 | 20 |
|---|---|---|---|---|---|---|
| Mn | 7 | 15 | 31 | 1023 | 32767 | 1048575 |
| Nn | 27 | 81 | 243 | 59049 | 14348907 | 3486784401 |
| Mn/Nn | 0.26 | 0.19 | 0.12 | 0.02 | 0.002 | 0.0003 |
Решение ханойской головоломки является примером подхода "разделяй и властвуй", в котором два рекурсивных вызова работают с приблизительно половиной входных данных. Такое постоянное деление на 2 быстро уменьшает размерность задачи (приводя, в нашем случае, к тривиальному переносу единственного диска).
Структура данных
В задачах поиска решений, часто приходится сохранять в памяти различные состояния решаемой задачи. Поэтому необходимо обеспечить максимально компактное описание состояния системы. Введём массив disks[i] размерности n, в котором будем хранить номер (начиная с 0) башни, где находится i-тый диск (также отсчет ведем с нуля): Эта функция объявляет класс Hanoi, экземпляры которого будут хранить число дисков nDisks, башен nTowers и массив disks принадлежностей каждого диска к конкретной башне. При помощи директивы prototype определим два метода класса Hanoi. Первый устанавливает диск под номерм disk на башню под номером tower, а второй выводит массив disks как строку: Теперь для 5 стержней и 3-х башен можно написать следующий код, который, при помощи оператора new, создаёт экземпляр han класса Hanoi, перемещает 0-й диск на 3-ю башню, а 4-й диск на 1-ю башню и затем результат выводится на страницу: что приведёт к появлению строки: .
Почти за всё приходится платить. Компактность представления информации замедляет доступ к ней. Например, чтобы получить номер диска, лежащего наверху башни tower, необходимо пробежаться по всем дискам: Аналогично выгдядит функция, возвращающая номер диска в стопке на башне (считая снизу от нуля):
Рисуем башни
Перейдём теперь к художествам при помощи библиотеки draw.js, которая позволяет рисовать как на канвасе, так и в создавать файлы векторной графики (svg-формат). Зададим внутри конструктора Hanoi геометрические параметры системы, добавив туда следующий код: (номер fly переносимого диска, его назначение flyDesи скорость flyV будут обсуждаться в следующем разделе). Теперь код метода рисования башен на объекте draw имеет вид: В библиотеке draw.js координаты ящиков - это их центр, а последний параметр функции box - радиус скругления углов.
В качестве теста создадим 3 башни и выведем их на html-страницу в виде svg-картинки:
Таймер
Для анимирования полёта перекладываемого диска нам потребуется 3 функции, при помощи которых диск берётся, бросается в направлении целевой башни и кладётся на неё, когда туда долетает: В этих функциях вводится переменная fly номера перекладываемого диска, его координаты, скорость, башня назначения и расстояние, которое он должен пролететь. Диск будет лететь, если в таймере вызывать функцию: Делается это следующим образом. На html странице помещается канвас: и пишется следующий скрипт:
Взаимодействие с мышкой
Для организации взаимодействия с мышкой напишем ещё одну функцию: Теперь необходимо подключть мышиное событие: Результат этих действий приведен в начале страницы.
Нерекурсивное решение
Чтобы анимировть перекладывание диска в процессе решения задачи компьютером, необходима нерекурсивная версия функций Hanoi1 или Hanoi2 Для её написания, понаблюдаем за действиями рекурсивной функции при различном числе дисков (компактная запись):
Hanoi2(2,1):
Hanoi2(3,1):
Hanoi2(4,1):
Hanoi2(5,1):
Видно, что через раз переносится самый маленький диск под номером 0 вправо (+0) для нечётного n или влево (-0) - для чётного. Несложно видеть, что после такой перестановки, существует только одна возможность переложить другой диск. Этим алгоритмом, как известно, и пользуются монахи:
Запуск скрипта (new Hanoi(4)).solveTXT(100) даёт:
Стековое решение
При помощи стека (массива "вызовов функций"), напишем ещё один нерекурсивный код, логика которого тождественна функции Hanoi1. Перед каждым рекурсивным вызовом, в стеке будем сохранять текущее состояние аргументов функции. Затем в стек запихнём рекурсивно вызываемую функцию. Кроме этого аргументов функции будем сохранять индекс pos, нумерующий "участки кода", куда необходимо вернуться по окончанию работы функции (в листинге Hanoi1 они помечены круглыми скобками): Запуск этой функции даёт результат аналогичный Hanoi1: . Нечто подобное функции Hanoi3 делает компьютер, когда запускает на выполнение рекурсивную функцию Hanoi1.
Финальный результат
Для запуска решателя следует нажать на кнопку и насладиться перемещением дисков: time = 0:0:0 moves = 0
Эти кольца имеют разные размеры и сложены в порядке возрастания, то есть меньшее помещается над большим. Существуют и другие варианты головоломки, в которых количество дисков увеличивается, но количество башен остается неизменным.
правила
Миссия состоит в том, чтобы переместить все диски в какую-то другую башню, не нарушая последовательность расположения. Вот несколько правил, которым нужно следовать для Ханойской башни:
Ниже приводится анимационное изображение решения головоломки Ханойской башни с тремя дисками.
Загадка Ханойской башни с n дисками может быть решена минимум за 2 n −1 шагов. Эта презентация показывает, что головоломка с 3 дисками прошла 2 3 — 1 = 7 шагов.
Итак, теперь мы можем разработать алгоритм для Ханойской башни с более чем двумя дисками. Разобьем стек дисков на две части. Самый большой диск (n- й диск) находится в одной части, а все остальные (n-1) — во второй части.
Наша конечная цель — переместить диск n из источника в место назначения, а затем поместить на него все остальные (n1) диски. Мы можем представить, чтобы применить это же рекурсивное решение для всего данного набора дисков.
Рекурсивный алгоритм для Ханойской башни может быть реализован следующим образом:

Разработка алгоритма решения игры Ханойские башни С++
Многие, наверное, знают эту игру. Есть три колышка, на первом стопка дисков, диаметр которых увеличивается к основанию стопки.

Необходимо переместить все эти диски на другой колышек. При этом нельзя перемещать одновременно более одного диска, нельзя класть больший диск над меньшим. Для временного размещения можно использовать третий колышек.
Эта задача решается очень просто – используем рекурсивную функцию. Рассмотрим сам алгоритм и реализацию в консольной программе на С++.
Допустим, нам необходимо переместить n дисков с колышка 1 на колышек 3.
При этом задача решается вот так:
Ханойская башня является одной из популярных головоломок XIX века. Эту задачу, иллюстрирующую рекурсию, очень любят программисты.
Несколько кружков разных размеров уложены друг на друга на один из стрежней, образуя башню. Задача: переставить башню на другое поле.
При перестановке должны соблюдаться некоторые правила.
1) кружки переставляются с одного стержня на другой, при этом их укладывают друг на друга, так что получаются маленькие башни. Нельзя откладывать кружки в сторону или ставить один кружок вместо другого;
2) при каждом ходе двигается только один кружок. Нельзя переносить несколько кружков одновременно. Например, запрещено брать по кружку в каждую руку;
3) можно брать кружок лишь с вершины какой–нибудь башни и класть его только на вершину другой башни. Нельзя брать кружок из середины башни или вставлять его в середину другой башни;
4) запрещено класть больший кружок на меньший.
На рисунке изображены несколько разрешенных и несколько запрещенных ходов.
Так можно: Так нельзя:
Эту романтическую легенду, придумал в 1883 году французский математик ЭДУАРД ЛЮКА.
Франсуа Эдуард Анатоль Люка (François Édouard Anatole Lucas; 4 апреля 1842, Амьен- 8 октября 1891) французский математик, профессор. Работал в лицее Лунле-Гран в Париже. Важнейшие работы Люка относятся к теории чисел и неопределенному анализу. Считал, что с помощью машин или каких-либо приспособлений сложение удобнее производить в двоичной системе, чем в десятичной.
• В 1878 г. Люка дал критерий для определения того, простым или составным является число Мерсенна Mp = 2p - 1, ныне известный как тест Люка — Лемера. Применяя свой метод, Люка установил, что M127 = 2127 − 1 — простое число. В течение 75 лет это число оставалось наибольшим простым числом, известным науке. Оно же позволило ему определить 12-е совершенное число.
• Первым обратил внимание и описал свойства чисел, впоследствии названными его именем - чисел Люка.
• Описал свойства последовательностей, удовлетворяющих однородным линейным рекуррентным уравнениям второго порядка, частным случаем которых являются числа Фибоначчи. Такие последовательности теперь называются последовательностями Люка.
• Придумал ряд интересных задач, в том числе известную головоломку Ханойская башня.
Где-то в непроходимых джунглях, недалеко от города Ханоя, есть монастырь бога Брахмы. В начале времен, когда Брама создавал Мир, он воздвиг в этом монастыре три высоких алмазных стержня и на один из них возложил 64 диска, сделанных из чистого золота. Он приказал монахам перенести эту башню на другой стержень (в соответствии с правилами, разумеется) С этого времени монахи работают день и ночь. Когда они закончат свой труд- наступит конец света.
III. Решение головоломки:
А) Формула зависимости ходов от числа кружков башни
Если составить таблицу зависимости ходов от числа кружков игры, то результат будет очевиден:
Число кружков : Оптимальное число ходов:
Получилась числовая последовательность: 1,3,7,15,31,.
Первое решение. Второе решение.
Если умножить предыдущее число на 2 и прибавить один, получим требуемое. 21 =2 ; 22=4; 23=8 ; 24=16; 25=32
7= 2*3+1 Вычитаем единицу из этих чисел, получаем нашу последовательность:
Обозначим n-ое число через a n , получаем формулу: 15= 24 -1
а 3 =2* а 2 + 1 an = 2n -1
B) Решение задачи на языке программирования.
Как уже говорилось во введении: Ханойская башня является одной из популярных головоломок XIX века.
Игра "Ханойские башни" состоит следующем. Есть N дисков и три стержня: А, В и С. В начальной конфигурации все диски надеты на один из стержней, образуя башню в виде пирамиды (меньшие диски в ней расположены поверх больших). Ход -> это перекладывание одного диска. Можно переместить верхний диск со стержня на стержень, но нельзя помещать больший диск поверх меньшего. Требуется указать последовательность ходов, перемещающих всю башню с исходного стержня на заданный.
Алгоритм решения задачи:
1. Если n>0, остановиться
2. Переместить верхние n-1 дисков со стержня А на стержень В, используя стержень С как вспомогательный.
3. Переместить оставшийся диск со стержня А на стержень С
4. Переместить n-1 дисков со стержня В на стержень С, используя стержень А как вспомогательный.
Нетрудно заметить, что этот алгоритм рекурсивный. Действительно, на шаге 2 и шаге 4 алгоритма требуется решить задачу, аналогичную первоначальной, только для меньшего числа дисков.
Рекурсивный алгоритм- это алгоритм, использующий в качестве вспомогательного самого себя.
Листинг программы на языке программирования Turbo Pascal.
PROGRAM hanoy; typebachnia =char; var a,b,c: bachnia; k, kol: integer;
procedure H (n: integer; a,b,c :bachnia); begin if n>0 then begin
H (n-1,a,c,b); write (‘переместить диск ’, n); writeln (a, ‘- > ,’ c); kol:=kol+1;
H (n-1,b,a,c); end; end;
begin write (‘ввести количество кружков =’); readln (k); a:=’A’; b:=’B’ ; c:=’C’;
H (k,a,b,c); writeln (‘количество шагов=', kol); end.
Результат тестирования программы
При количестве кружков К=3
переместить диск 1 А - > С
переместить диск 2 А - > В
переместить диск 1 С - > В
переместить диск 3 А - > С
переместить диск 1 В - > А переместить диск 2 В - > С
переместить диск 1 А - > С
КОЛИЧЕСТВО ШАГОВ = 7
(проверка формулы 2n -1 = 23 -1=7 шагов)
При количестве кружков К=4 переместить диск 1 А - > В переместить диск 2 А - > С переместить диск 1 В - > С переместить диск 3 А - > В переместить диск 1 С - > А переместить диск 2 С - > В переместить диск 1 А - > В переместить диск 4 А - > С переместить диск 1 В - > С переместить диск 2 В - > А переместить диск 1 С - > А переместить диск 3 В - > С переместить диск 1 А - > В переместить диск 2 А - > С переместить диск 1 В - > С
КОЛИЧЕСТВО ШАГОВ = 15
(проверка формулы 2n -1 = 24 -1=15 шагов)
Листинг программы на языке программирования QBasic.
REM ОСНОВНАЯ ПРОГРАММА
INPUT “введите N=”;N
PRINT “количество шагов=”; kol
REM РЕКУРСИВНАЯ ПОДПРОГРАММА
1: IF N=0 THEN RETURN
PRINT “переместить диск “;N ; A; “->”;C
Если использовать полученную формулу из п. III , раздела А) то можно подсчитать, что свою работу они закончат за ( 264 -1) шагов.
264 = 24 * 260 = 16* 260 ( 16 * (210 ) 6 ( 16*(10 3)6 ( 16 *1018 т. к. 210 = 1024 ( 1000 = 10 3 получили, что число ходов приблизительно равно шестнадцати квинтильонам.
В одних сутках 24 часа, в часе 60*60=3600 секунд.
Значит, в сутках 24* 3600= 86 400 секунд
В году- в 365 больше, т. е. приблизительно 32 миллиона секунд, или 32 * 106 секунд
Чтобы узнать, сколько лет необходимо монахам, нужно разделить одно из полученных нами чисел на другое:
(16 *1018 ) / (32 * 106 ) = 0,5 * 10 12 = 500 000 000 000 лет
D) Решение задачи на суперкомпьютере.
Представим себе вместо монахов будущий суперкомпьютер: Пусть он совершает в секунду 1 миллиард операций. Сколько времени понадобиться компьютеру переложить башню из 64 кружков?
Т. к. компьютер работает в миллиард раз быстрее монахов, то ему понадобиться в миллиард раз меньше времени - всего 500 лет.
Существует одна притча:
«Спорили два друга:
-Мир давно уже должен быть погибнуть!
-Почему ты так думаешь?
-Знаешь, существует древнее предание, по которому стоит перенести всего лишь 64 кружка и наступит конец света
- Всего лишь 64, стоит задуматься, что если один ход проделывать за 1 секунду, то в час можно сделать 3 600 перенесений
- А в сутки- около ста тысяч. В десять дней- миллион ходов. Миллионом же ходов можно, я уверен, перенести хоть тысячу кружков.
- Ошибаешься. Чтобы перенести всего 64 кружка, нужно уже круглым счетом 500 миллиардов лет!
Хочется сказать, что игры и головоломки – восхитительный мир для применения программирования , развития логического и алгоритмического мышления.
Читайте также:


