Что такое соотношение сторон прямоугольника
Соотношение сторон из геометрической формы представляет собой отношение его размеров в разных измерениях. Например, соотношение сторон прямоугольника - это отношение его длинной стороны к более короткой стороне - отношение ширины к высоте, когда прямоугольник ориентирован как «пейзаж».
Соотношение сторон чаще всего выражается двумя целыми числами, разделенными двоеточием (x: y), реже - простой или десятичной дробью . Значения x и y представляют не фактическую ширину и высоту, а скорее соотношение между шириной и высотой. Например, 8: 5, 16:10, 1,6: 1, 8 ⁄ 5 и 1,6 - все способы представления одного и того же соотношения сторон.
В объектах с более чем двумя измерениями, таких как гипер прямоугольники , соотношение сторон можно определить как отношение самой длинной стороны к самой короткой стороне.
СОДЕРЖАНИЕ
Приложения и использование
Этот термин чаще всего используется в отношении:
- Графика / изображение
- Фотолитография : соотношение сторон вытравленной или осажденной структуры - это отношение высоты ее вертикальной боковой стенки к ее ширине.
Соотношение сторон простых форм
Прямоугольники
Для прямоугольника соотношение сторон обозначает отношение ширины к высоте прямоугольника. У квадрата минимально возможное соотношение сторон 1: 1.
- 4: 3 = 1,3 : некоторые (не все) компьютерные мониторы 20-го века ( VGA , XGA и т. Д.), Телевидение стандартной четкости
- 2 : 1 знак равно 1,414 . >: 1 = 1,414 . > : международные форматы бумаги ( ISO 216 )
- 3: 2 = 1,5: фотопленка 35 мм , iPhone (до iPhone 5 ) отображает
- 16:10 = 1,6: широко используемые широкоформатныекомпьютерные дисплеи ( WXGA )
- Φ: 1 = 1,618 . золотое сечение , близкое к 16:10
- 5: 3 = 1. 6 : супер 16 мм , стандартный датчик пленки во многих европейских странах
- 16: 9 = 1. 7 : широкоэкранный телевизор
- 2: 1 = 2: домино
- 64:27 = 2. 370 : сверхширокий экран, 21: 9
- 32: 9 = 3. 5 : супер ультра-широкоформатный
Эллипсы
Для эллипса соотношение сторон обозначает отношение большой оси к малой оси . Эллипс с соотношением сторон 1: 1 - это круг.
Соотношение сторон общих форм
В геометрии существует несколько альтернативных определений соотношений сторон общих компактов в d-мерном пространстве:
- Соотношение диаметра и ширины (DWAR) компактного набора - это отношение его диаметра к его ширине. У круга минимальный DWAR равен 1. У квадрата есть DWAR равный . 2 >>
- Соотношение сторон куба и объема (CVAR) компактного набора - это корень d-й степени из отношения d- объема наименьшего окружающего параллельного осям d- куба к собственному d- объему набора . Квадрат имеет минимальный CVAR, равный 1. У круга CVAR равен . Прямоугольник, параллельный оси шириной W и высотой H , где W > H , имеет CVAR . 2 >> W 2 / W ЧАС знак равно W / ЧАС / WH>> = >>
Если размер d фиксирован, то все разумные определения соотношения сторон эквивалентны с точностью до постоянных коэффициентов.
Обозначения
Соотношения сторон математически выражаются как x : y (произносится как «x-to-y»).
Кинематографические соотношения сторон обычно обозначаются как (округленное) десятичное число, кратное ширине и единице высоты, тогда как фотографические и видеографические соотношения сторон обычно определяются и обозначаются целочисленными отношениями ширины к высоте. В цифровых изображениях существует тонкое различие между соотношением сторон дисплея (изображение в том виде, в каком оно отображается) и соотношением сторон хранилища (соотношением размеров в пикселях); см. Отличия .
Это Golden Ratio / National Geographic соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.
Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.
«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons
«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons
Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.
Почему золотое сечение так популярно
Впервые им заинтересовались M. Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.
Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали S. Strogatz. Proportion Control / The New York Times Opinionator «божественной пропорцией».
Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно M. Livio. The Golden Ratio: The Story of PHI, the World’s Most Astonishing Number как никакое другое в математике.
Его можно встретить в природе
Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.
Часть растения эониума. Фото: Max Ronnersjö / Wikimedia Commons
Его обнаруживают в произведениях архитектуры и искусства
Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.
Почему универсальность золотого сечения — миф
Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.
Божественность золотого сечения преувеличивается
Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали S. Strogatz. Proportion Control / The New York Times Opinionator из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.
Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.
В природе золотое сечение не так уж распространено
Его находят далеко не Golden Ratio / National Geographic везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие J. Sharp. Spirals and the Golden Section / Nexus Network Journal . У них больше витков, и расстояние между ними меньше. Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:
Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons
Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons
В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.
В искусстве оно тоже встречается не так уж часто
Изучение 565 картин выдающихся художников показало A. Olariu. Golden Section and the Art of Painting / arXiv Preprints , что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят M. Livio. The golden ratio and aesthetics / Plus Magazine его даже в произведениях Леонардо да Винчи.
Археологические исследования не подтверждают P. Foutakis. Did the Greeks Build According to the Golden Ratio? / Cambridge Archaeological Journal и того, что древние греки могли использовать золотое сечение при постройке Парфенона. Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.
Кому золотое сечение может быть полезно на самом деле
Современная математика использует S. C. Carlson. Golden ratio / Britannica золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.
Фрактальная форма кочана капусты Романеско. Фото: Ivar Leidus / Wikimedia Commons
Знание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.
Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал Ф. П. Варпаховский, А. Н. Колмогоров. О решении десятой проблемы Гильберта / Квант , что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.
На протяжении веков «золотое сечение» считается самым прекрасным соотношением в искусстве и архитектуре.

«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».
Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».
Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:

Что эквивалентно пропорции:

Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».
«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.
Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.

На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.е. бесконечная десятичная дробь, не имеющая периода.
Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.

Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.

Шаг 1. Сделаем перекрестное умножение:

Шаг 2. Приведем уравнение к 0:

Шаг 3. Решим квадратное уравнение:

Поскольку мы работаем с длинами, нам нужно только положительное решение:

Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:

Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя. Это потрясающе!
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку "Вычислить". Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).
 |
Можно дать и другое определение прямоугольника.
Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.
Свойства прямоугольника
Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.
- 1. Стороны прямоугольника являются его высотами.
- 2. Все углы прямоугольника прямые.
- 3. Квадрат диагонали прямоугольника равен сумме квадратов его соседних двух сторон.
- 4. Диагонали прямоугольника равны.
- 5. Около любого прямоугольника можно описать окружность, при этом диаметр описанной окружности равна диагонали прямоугольника.
Длиной прямоугольника называется более длинная пара его сторон.
Шириной прямоугольника называется более короткая пара его сторон.
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
 |
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 |
Из равенства (1) найдем d:

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:
 |

Ответ:
Окружность, описанная около прямоугольника
Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):
 |
Формула радиуса окружности описанной около прямоугольника
Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.
Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть
Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:
 |
 |

Ответ:
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
где \( \small a \) и \( \small b \) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:
 |

Ответ:
Формулы сторон прямоугольника через его диагональ и периметр
Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).
Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:
 | (6) |
 | (7) |
Из формулы (7) найдем \( \small b \) и подставим в (6):
 | (8) |
 | (9) |
Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):
Вычислим дискриминант квадратного уравнения (10):
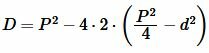 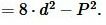 | (11) |
Сторона прямоугольника вычисляется из следующих формул:
После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).
Примечание. Легко можно доказать, что
Имеем \( \small \sqrt <2d ,\) \( \small P > 2d .\) Следовательно выполняется неравенство (*).
Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.
Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):
 |
Подставляя значения и в первую формулу (12), получим:
 |
Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:
 |
Ответ: ,
Признаки прямоугольника
Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.
Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.
Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.
Читайте также:


