Что такое шестеренка в компьютере
Уважаемый читатель, наверняка ты прекрасно знаешь, что такое шестеренка или по другому зубчатое колесо.
Изобретение зубчатых колес - это большое достижение человека.
Сама по себе идея механической передачи восходит к идее колеса. Применяя систему из двух колёс разного диаметра, можно не только передавать, но и преобразовывать движение. Эта передача удобна там, где требуется «усилить движение», например, при подъеме тяжестей.
Шестеренки были изобретены человеком в древности, как раз для усиления крутящегося момента, для подъема тяжестей.
По крайней мере в Древнем Египте уже использовали первые примитивные шестеренки.
Для орошения земель уже использовались приводимые в действие быками устройства, состоявшие из деревянной зубчатой передачи и колеса с большим числом ковшей.
Вместо зубьев первоначально использовали деревянные цилиндрические или прямоугольные пальцы, которые устанавливали по краю деревянных ободьев.
Изготовленный в I веке до н.э. Антикитерский механизм состоял из десятков металлических зубчатых колес и содержал не менее 30 бронзовых шестерёнок в прямоугольном деревянном корпусе.
Этот механизм был астрономическим прибором и использовался для расчёта движения небесных тел.
Сейчас шестеренки можно встретить во многих устройствах, например, в часах.
В затворе плотины
И еще много где.
А теперь, внимание, вопрос на засыпку, уважаемый читатель.
Представь себе ситуацию, ты идешь по дороге и вдруг видишь на асфальте лежит шестерня.
Ответь для себя честно. С какой вероятностью ты бы подумал о том, что эта шестеренка могла бы образоваться сама собой в результате эволюции?
Чтобы ты вообще сказал о разуме человека, который бы стал твердить - что это результат эволюции и эта шестеренка сама собой образовалась, например, кусок металла за миллионы лет стал тереться там о что-нибудь и сформировал шестерню?
Ведь сама идея передачи усилия через зубчатые колеса - все это идея РАЗУМА, изобретателя, механика. У которого была цель - что-то поднять, передать крутящийся момент, передать усилие,
Вообще, чтобы создать шестеренку, которая бы работала как надо, нужно учитывать много факторов, такие как количество зубьев, шаг зубьев, высота головки зубьев, диаметр окружности еще много других.
В механике есть формулы, позволяющие рассчитать все параметры шестеренок.
Очевидно, что это продукт инженерной мысли. Никто не будет использовать шестеренку просто так, не зная куда ее вставить.
Мало спроектировать, потом шестеренку надо изготовить, нарезать
Или на худой конец отлить в форме, как это делали в Китае, 200 лет до Рождества Христова.
Чтобы изготовить и использовать шестеренку нужно:
- Осознать необходимость, где нужно ее использовать.
- Выбрать нужный вид шестеренки
- Спроектировать ее с точки зрения необходимых качеств
- Изготовить
- Включить в состав конечного изделия
Все это невозможно сделать само собой, это все результат
- РАЗУМА
- ЦЕЛИ
- ПЛАНИРОВАНИЯ
- УСИЛИЙ
- РАЗУМНОГО ЗАМЫСЛА КОНЕЧНОГО ИЗДЕЛИЯ
Никаким образом эволюционным образом шестеренка не может быть произведена.
А теперь самое главное, внимание!
Issus coleoptratus — вид прыгающих насекомых из семейства иссид (цикад).
Размер тела составляет 5,5—7,0 мм в длину.
В 2013 году ученые с большим удивлением обнаружили в ее конструкции самые настоящие шестеренки, зубчатые колеса, позволяющие ей прыгать.
У личинок этого насекомого есть небольшие наросты в форме шестерни на каждой из пар задних ног. Эти наросты имеют зубцы, которые цепляются друг за друга. Размер механизма около 400 микрометров.
Эти шестерни являются первым действующим зубчатым зацеплением, обнаруженным в естественном мире. Благодаря сочетанию анатомического анализа и высокоскоростного видеозахвата, ученые из Кембриджского университета узнали, что шестеренчатая передача, гордость человеческого гения, на самом деле уже давно «изобретена».
Больше ни у кого таких шестеренок нет!
И эти шестеренки действуют только на определенной стадии развития личинки, потом за ненадобностью отпадают.
Интересно, что зубчатая передача в ногах насекомого имеет ряд особенностей, которые применяются в современных коробках передач автомобилей и других механизмах.
Так, каждый зуб на ноге насекомого имеет закругленный угол, амортизирующий удары во время прокручивания и предотвращающий сдвиг зубьев. При этом природная «коробка передач» выполнена с очень высокой точностью , особенно если учесть, что вся «шестеренка» имеет длину всего лишь 400 микрометров и насчитывает 10-12 зубьев.
Все еще думаете, что шестеренки в цикадах продукт эволюции?
Вспомните, что вы ранее подумали о разуме человека, который утверждает, что механизм сцепления, зубчатых колес, мог бы быть плодом эволюции?
Это уникальный пример, явно указывающий на РАЗУМ ТВОРЦА.
Никакая эволюция не могла дать шестеренки, для этого у нее нет ни цели, ни разума, ни способности спланировать, ни разумного замысла как и где будут использоваться шестеренки.
Но Бог дал это этим насекомым, запрограммировав в ДНК (программе развития) появление этих шестеренок. И я не исключаю, что Он это сделал для того, чтобы показать, спустя много тысяч лет, что именно БОГ Творец всего, Он первый, кто использовал шестеренки в конструкциях, а совсем не человек.
И только потому, что человек имеет разум, данный ему Богом, ПОЭТОМУ человек оказался способен изобрести и использовать шестеренки.
Но ИЗНАЧАЛЬНО, эта идея БОГА, подумайте об этом.
Мир - это продукт РАЗУМА, разумного замысла ТВОРЦА, а не продукт случайной эволюции.
И этот Творец скоро грядет в этот мир, чтобы судить его за неверие.
Пересмотри свои взгляды, покайся, пока есть время.
Познакомиться с тем, что нравится Творцу, а что нет, как жить и что делать ты можешь в специальной книге инструкции, которую Он оставил на земле - в Слове Божьем, в Библии.
Тот, кто придумал шестеренку для личинки цикады и сохранил ее в тайне до 2013 года, поверь, смог сохранить Свое Слово живым и действенным, чтобы спасти твою душу и в этом мире и в вечности.
Где вы оказались? Вы на канале " Ключи разумения. Апокалипсис " - то, что вы хотели знать о Боге, Библии, но вам не рассказали. А мы рассказываем ясно и просто, с картинками. Отвечаем на сложные вопросы. Вы здесь не случайно , поэтому обязательно подпишитесь на наш канал, чтобы не пропустить новые статьи. Мы пишем, чтобы вы могли найти вечную жизнь и мир с Богом. Нас лучше всего читать по порядку с самого первого поста и далее.
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.
Отписаться от уведомлений вы всегда сможете в профиле автора.
Про моделирование и печать шестеренок здесь написано достаточно. Однако, большинство статей предполагают использование спец. программ. Но, у каждого пользователя есть своя «любимая» программа для моделирования. Кроме того, не все хотят устанавливать и изучать дополнительный софт. Как же моделировать профиль зуба шестерни в программе, где не предусмотрено вычерчивание эвольвентного профиля? Очень просто! Но муторно… :)
Нам понадобится любая программа, которая может работать с 2D графикой. Например, ваша любимая программа! Она работает с 3D? Значит и с 2D сможет! ;) Строим профиль эвольвентного зуба без коррекции. Если кому-то захочется построить корригированный зуб, он может с этим разобраться самостоятельно. Информации полно - и в интернете, и в литературе. Если в вашей шестеренке зубьев больше 17-ти, то вам коррекция не понадобится. Если же зубьев 17 или меньше, то без коррекции возникает «утоньшение» ножки зуба, а при чрезмерной коррекции возникает заострение вершины зуба. Что выбрать? Решать вам.
Определяем делительную окружность шестерни. Зачем это нужно? Чтобы определить межосевое расстояние. Т.е. где у вас будет располагаться одна шестерня, а где другая. Сложив диаметры делительных окружностей шестеренок и разделив сумму пополам, вы определите межосевое расстояние.
Чтобы определить диаметр делительной окружности нужно знать два параметра: модуль зуба и количество зубьев. Ну, с количеством зубьев – тут всем все понятно. Количеством зубьев на одной и другой шестерне определяется нужное нам передаточное отношение. Что такое модуль? Чтобы не связываться с числом «пи», инженеры придумали модуль. :) Как вы знаете из курса школьной математики: D= 2 «Пи» R. Так вот, что касается шестеренок, там D = m* z, где D – это диаметр делительной окружности, m – модуль, z – количество зубьев. Модуль – величина, характеризующая размер зуба. Высота зуба равна 2,25 m. Модуль принято выбирать из стандартного ряда величин: 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32 (ГОСТ-9563). Можно ли придумать «свой» модуль? Конечно! Но ваша шестеренка будет нестандартная! ;)
Чертим делительную окружность. У кого нет подходящей «проги», чертит на бумаге, фанере или металле! :) От делительной окружности «откладываем» наружу на величину модуля (m) окружность вершин зубьев. Внутрь откладываем модуль и еще четверть модуля (1,25 m) - получаем окружность впадин зубьев. Четверть модуля дается на зазор между зубом другой шестерни и впадиной этой шестерни.
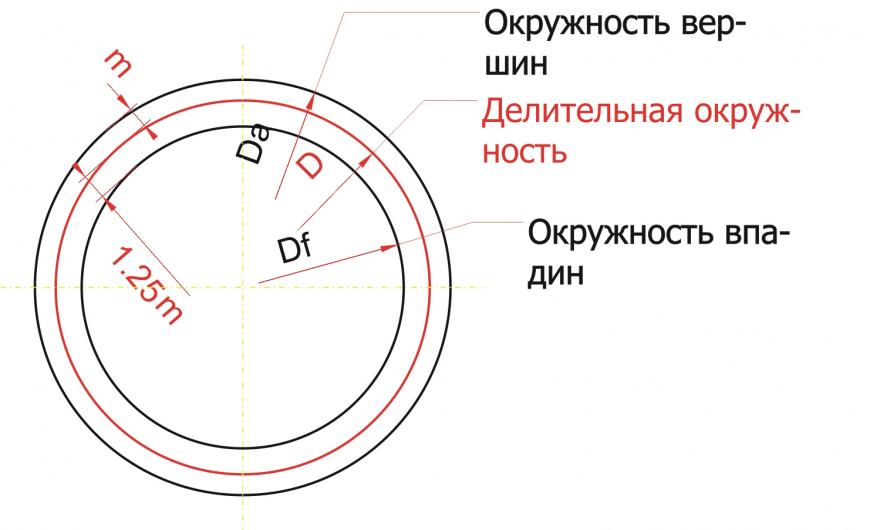
Строим основную окружность. Основная окружность – это окружность, по которой «перекатывается» прямая линия, своим концом вычерчивая эвольвенту. Формула для расчета диаметра основной окружности очень простая: Db = D * cos a, где а – угол рейки 20 градусов. Эта формула нам не нужна! Все гораздо проще. Строим прямую линию через любую точку делительной окружности. Удобнее взять самую высокую точку, на «12 часов». Тогда линия будет горизонтальная. Повернем эту линию на угол в 20 градусов против часовой стрелки. Можно ли повернуть на другой угол? Думаю, можно, но не нужно. :) Кому интересно, ищем в литературе или интернете ответ на вопрос.
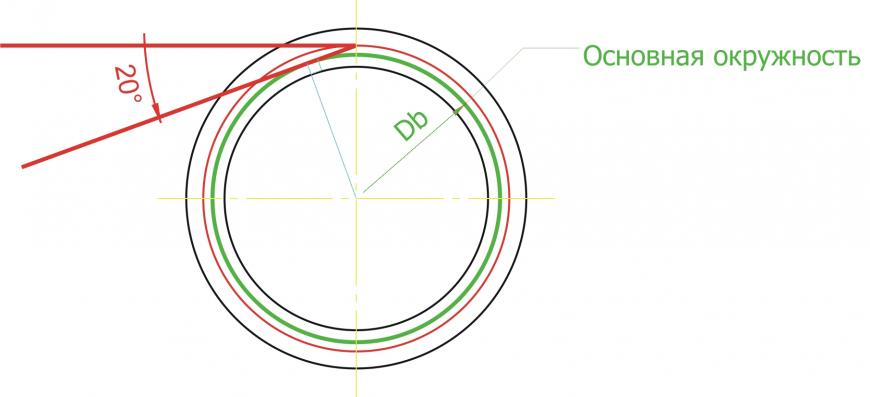
Прямую линию, которую мы получили, будем поворачивать вокруг центра шестерни маленькими угловыми шагами. Но, самое главное, при каждом повороте против часовой стрелки будем удлинять нашу линию на длину той дуги основной окружности, которую она прошла. А при повороте по часовой стрелки наша линия будет укорачиваться на ту же величину. Длину дуги или мерим в программе, или считаем по формуле: Длина дуги = (Пи * Db * угол поворота (в градусах)) / 360
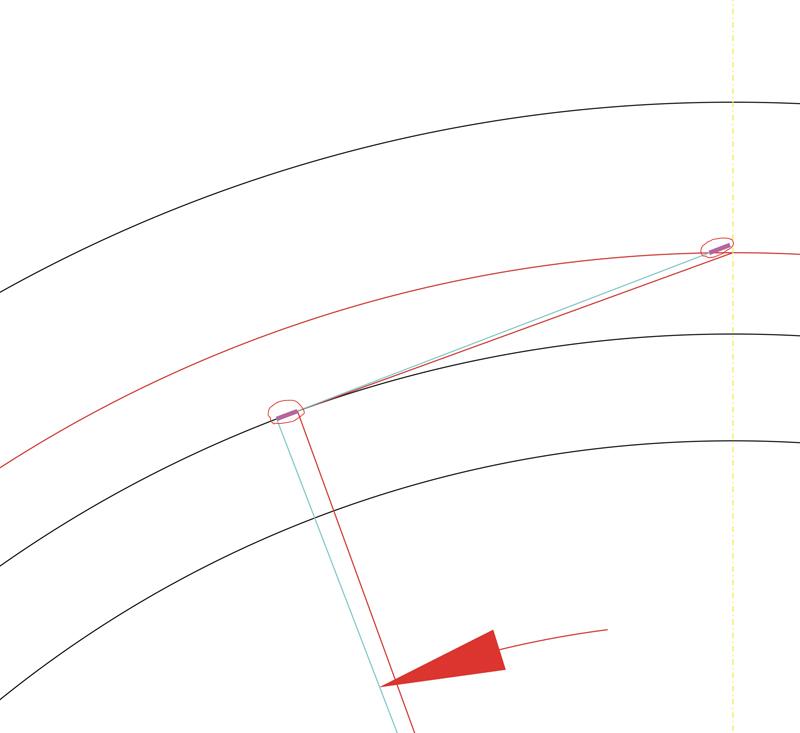
«Прокатываем» прямую линию по основной окружности с нужным угловым шагом. Получаем точки эвольвентного профиля. Чем точнее хотим строить эвольвенту, тем меньший угловой шаг выбираем.
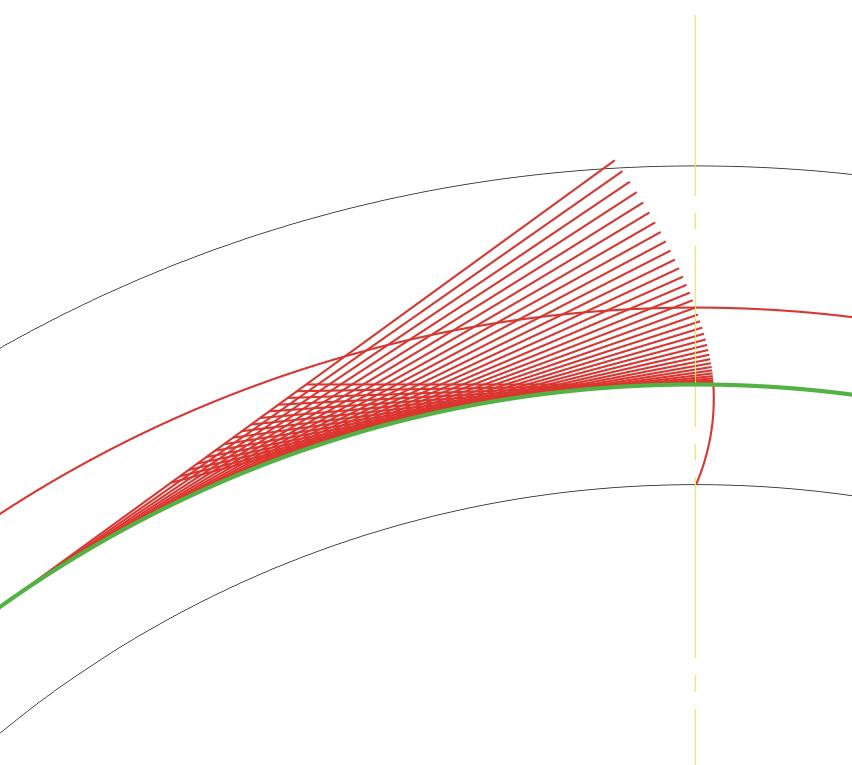
К сожалению, в большинстве программ автоматического проектирования (CAD) не предусмотрено построение эвольвенты. Поэтому эвольвенту строим по точкам либо прямыми, либо дугами, либо сплайнами. При построении эвольвента заканчивается на основной окружности. Оставшуюся часть зуба до впадины можно построить дугой того же радиуса, который получается на трех последних точках. Для 3D печати я рисовал эвольвенту сплайнами. Для лазерной резки металла мне пришлось рисовать эвольвенту дугами. Для лазера нужно создать файл в формате dwg или dxf (для некоторых, почему-то, только dxf). «Понимает» лазер только прямые, дуги и окружности, сплайны не понимает. На лазере можно сделать только прямозубые шестерни.
Делим окружность на такое количество частей, которое в 4 раза больше количества зубьев шестерни. Эвольвенту отзеркаливаем относительно оси зуба и копируем с поворотом нужное количество раз.

Чтобы получить шестерню в объеме, то задаем толщину и получаем прямозубую цилиндрическую шестерню:

Если нужна косозубая шестерня, то вводим наклон зубьев и получаем:

Для получения шевронной шестерни, нужно отзеркалить косозубую шестерню относительно нужной торцевой поверхности:

Как смоделировать коническую шестерню, придумайте сами. :)
К вопросу о точности шестеренок. Те шестеренки, которые я распечатал на 3D принтере, сначала вращались, издавая легкое поскрипывание. Прошло некоторое время, и звук прекратился. Шестеренки «притерлись». :)
После модернизации принтера, шестеренки не печатал. Возможно, сейчас они напечатаются более точно, и не будут скрипеть.
Для вакуумной машины смоделировал пару – «шестерня-рейка». Их вырезали на лазере:
Рейка будет перемещать прижимную рамку с материалом (листовой АБС) из области нагрева в область вакуумного формования. Рейка и шестерня еще не испытывались. Возможно, придется «дорабатывать напильником». На рейке и шестерне видны «волны» от лазера – слишком толстый металл. Они то и могут заклинить. А, может, разработается. :) Время покажет!Подпишитесь на автора
Подпишитесь на автора, если вам нравятся его публикации. Тогда вы будете получать уведомления о его новых статьях.

Зубча́тое колесо (обыв. шестерня́) — основная деталь зубчатой передачи в виде диска с зубьями на цилиндрической или конической поверхности, входящими в зацепление с зубьями другого зубчатого колеса. В машиностроении принято малое ведущее зубчатое колесо независимо от числа зубьев называть шестернёй, а большое ведомое — колесом. Однако часто все зубчатые колёса называют шестерня́ми.
Зубчатые колёса обычно используются па́рами с разным числом зубьев с целью преобразования вращающего момента и числа оборотов вала на выходе. Колесо, к которому вращающий момент подводится извне, называется ведущим, а колесо, с которого момент снимается — ведомым. Если диаметр ведущего колеса меньше, то вращающий момент ведомого колеса увеличивается за счёт пропорционального уменьшения скорости вращения, и наоборот.
Следует заметить, что зубчатая передача не является усилителем механической мощности, так как общее количество механической энергии на её выходе не может превышать количество энергии на входе. Это связано с тем, что механическая работа в данном случае будет пропорциональна произведению вращающего момента на скорость вращения. В соответствии с передаточным отношением, увеличение крутящего момента будет вызывать пропорциональное уменьшение угловой скорости вращения ведомой шестерни, а их произведение останется неизменным. Данное соотношение справедливо для идеального случая, не учитывающего потери на трение и другие эффекты, характерные для реальных устройств.
Содержание
Поперечный профиль зуба
Движение точки соприкосновения зубьев с эвольвентным профилемБоковая форма профиля зубьев колёс для обеспечения плавности качения может быть: эвольвентной, неэльвовентной передача Новикова (с одной и двумя линиями зацепления), циклоидальной. Кроме того, в храповых механизмах применяются зубчатые колёса с несимметричным профилем зуба.
Продольная линия зуба
Прямозубые колёса
Прямозубые колёса — самый распространённый вид зубчатых колёс. Зубья являются продолжением радиусов, а линия контакта зубьев обеих шестерён параллельна оси вращения. При этом оси обеих шестерён также должны располагаться строго параллельно.
Косозубые колёса
Косозубые колёса являются усовершенствованным вариантом прямозубых. Их зубья располагаются под углом к оси вращения, а по форме образуют часть спирали. Зацепление таких колёс происходит плавнее, чем у прямозубых, и с меньшим шумом.
Недостатками косозубых колёс можно считать следующие факторы:
- При работе косозубого колеса возникает механический момент, направленный вдоль оси, что вызывает необходимость применения для установки вала упорных подшипников;
- Увеличение площади трения зубьев (что вызывает дополнительные потери мощности на нагрев), которое компенсируется применением специальных смазок.
В целом, косозубые колёса применяются в механизмах, требующих передачи большого крутящего момента на высокой скорости, либо имеющих жёсткие ограничения по шумности.
Колёса с круговыми зубьями
Передачи на основе колёс с круговыми зубьями имеют ещё более высокие ходовые качества, чем косозубые — высокую плавность и бесшумность работы. Однако они ограничены в применении сниженными, при тех же условиях, КПД и ресурсом работы, такие колёса заметно сложнее в производстве. Линия зубьев у них представляет собой окружность радиуса, подбираемого под определённые требования.
Двойные косозубые колёса (шевроны)
Двойные косозубые колёса решают проблему осевого момента. Зубья таких колёс изготавливаются в виде буквы «V» (либо они получаются стыковкой двух косозубых колёс со встречным расположением зубьев). Осевые моменты обеих половин такого колеса взаимно компенсируются, поэтому отпадает необходимость в установке осей и валов в специальные подшипники. Передачи, основанные на таких зубчатых колёсах, обычно называют «шевронными».
Зубчатые конические колёса

Кроме наиболее распространёных циллиндрических З. к. применяются колёса конической формы. Конические колёса применяются там, где необходимо передать крутящий момент под определённым углом. Такие конические колёса с круговым зубом, например, применяются в автомобильных дифференциалах, используемых для передачи момента от двигателя к колёсам.
Секторные колёса
Секторное колесо представляет собой часть обычного колеса любого типа. Такие колёса применяются в тех случаях, когда не требуется вращение механизма на 360°, и поэтому можно сэкономить на его габаритах.
Зубчатые колёса с внутренним зацеплением
При жёстких ограничениях на габариты, в планетарных механизмах, в шестерённых насосах с внутренним зацеплением, в приводе башни танка, удобно применение колёс с зубчатым венцом, нарезанным с внутренней стороны. Также сто́ит заметить, что вращение ведущего и ведомого колеса направленно в одну сторону. В такой передаче меньше потери на трение, т.е. выше КПД.
Реечная передача (кремальера)
Реечная передача (кремальера) применяется в тех случаях, когда необходимо преобразовать вращательное движение в поступательное и обратно. Состоит из обычной прямозубой шестерни и зубчатой планки (рейки). Работа такого механизма показана на рисунке.
Коронные колёса

Коронное колесо — особый вид колёс, зубья которых располагаются на боковой поверхности. Такое колесо обычно стыкуется с обычным прямозубым, либо с барабаном из стержней (цевочное колесо), как в башенных часах.
Изготовление зубчатых колёс

Основные методы изготовления зубчатых колёс: метод копирования, когда режущие кромки инструмента соответствуют форме впадины зубчатого колеса и после нарезания одной впадины заготовка поворачивается на один зуб при помощи делительного устройства, метод обкатки, (обрабатывающий инструмент воспроизводит движение пары зубчатых колёс), горячее и холодное накатывание.
Технологиями изготовления зубчатых колёс занимаются специальные направления технологии машиностроения и области станкостроения. Основные производители металлорежущих станков зубообрабатывающей группы в России — заводы «Комсомолец» (г. Егорьевск) и Коломенский тяжёлого станкостроения (г. Коломна).

Среди предметов, поднятых с затонувшего корабля, оказался бесформенный ком корродированной бронзы, покрытой известковыми отложениями, принятый сначала за обломок статуи. В 1902 году его изучением занялся археолог Валериос Стаис. Расчистив его от известковых отложений, он, к своему удивлению, обнаружил сложный механизм, наподобие часового, с множеством бронзовых шестеренок, остатками приводных валов и измерительных шкал. Также удалось разобрать некоторые надписи на древнегреческом языке.
Пролежав 2000 лет на морском дне, механизм дошел до нас в сильно поврежденном виде. Деревянный каркас, на котором он, по всей видимости, крепился, полностью распался. Металлические детали сильно деформировались и подверглись коррозии. Кроме того, многие фрагменты механизма были утрачены.
В 1903 году в Афинах вышла первая официальная научная публикация с описанием и фотографиями Антикитерского механизма, как было названо это устройство.

Прайс предполагал, что Антикитерский механизм был создан около 85-80 г. до н.э. Однако радиоуглеродный анализ (1971) и эпиграфические исследования надписей отодвинули предполагаемое время его создания до 150-100 гг. до н.э.
В 1978 г. известный французский исследователь Жак-Ив Кусто еще раз обследовал место находки, но не нашел больше останков Антикитерского механизма.
Большой вклад в изучение Антикитерского механизма внес Майкл Райт, сотрудник Лондонского музея науки и Имперского колледжа в Лондоне, применивший для исследования оригинальных фрагментов метод линейной рентгеновской томографии. Первые результаты этого исследования были представлены в 1997 году, что позволило существенно скорректировать выводы Прайса.
Продолжает свои исследования и Майкл Райт, представивший в 2007 году модифицированную модель Антикитерского механизма.
Совместными усилиями исследователей Антикитерский механизм постепенно открывает свои тайны, расширяя наши представления о возможностях античной науки и техники.
Оригинальные фрагменты
Все сохранившиеся металлические части Антикитерского механизма изготовлены из листовой бронзы толщиной 1-2 миллиметра. Многие фрагменты практически полностью преобразовались в продукты коррозии, однако во многих местах все еще можно различить изящные детали механизма.
В настоящее время известно 7 больших (A-G) и 75 малых фрагментов Антикитерского механизма.

Фото 1. Антикитерский механизм, фрагменты A-G. Радиография. Масштаб не соблюден

Фото 3. Антикитерский механизм, фрагмент A
Фрагмент B, размером около 124 миллиметра (фото 4) состоит в основном из оставшейся части верхнего циферблата задней панели с двумя сломанными валами и следами еще одной шестеренки. Фрагменты A и B примыкают друг к другу, в то время как фрагмент E, размером около 64 миллиметров, на котором расположена еще одна небольшая часть циферблата, помещается между ними. Соединенные вместе, они позволяют рассмотреть устройство задней панели, состоящей из двух больших циферблатов, имеющих вид спирали из четырех и пяти концентрических сходящихся колец, расположенных один над другим на прямоугольной пластине, высота которой примерно в два раза больше ширины. На недавно обнаруженном фрагменте F также располагается кусочек заднего циферблата со следами деревянных деталей, образующих сочленение в углу пластины.

Фото 4. Антикитерский механизм, фрагмент B
На всех этих фрагментах можно различить следы бронзовых пластин, располагавшихся поверх циферблатов. Они были плотно заполнены надписями. Некоторые их кусочки удалили с поверхности основных деталей в процессе очистки и хранения, другие же снова собрали в то, что ныне известно в качестве фрагмента G. Оставшимся разрозненным частям, в основном это мельчайшие кусочки, присвоили номера.

Фото 5. Антикитерский механизм, фрагмент C

Фото 6. Антикитерский механизм, фрагменты B, A и C (слева направо): вид сзади
Фрагмент D состоит из двух колесиков, совмещенных друг с другом посредством тонкой плоской пластины, проложенной между ними. Данные колесики имеют не совсем круглую форму, вал, на которых они должны располагаться, отсутствует. Для них не находится места на прочих дошедших до нас фрагментах и, таким образом, их назначение установить не удается.
Все фрагменты Антикитерского механизма хранятся в Национальном археологическом музее в Афинах. Фрагменты A, B и C демонстрируются в экспозиции музея.
Фото 7. Антикитерский механизм, фрагмент D
Назначение и функции
По уровню миниатюризации и сложности Антикитерский механизм сопоставим с астрономическими часами XVIII века. Он содержит более 30 шестеренок с зубьями в форме равносторонних треугольников. Столь высокая сложность и безупречное изготовление позволяют предположить, что у него имелся ряд предшественников, которые не были обнаружены.
Таким образом, существование в древности механизмов, сопоставимых по сложности с Антикитерским, находит подтверждение у античных авторов, хотя ни один из них не дошел до нас.

Компьютерная реконструкция механизма
Дальнейшие исследования подтвердили, что Антикитерский механизм являлся астрономическим и календарным калькулятором, использовавшимся для прогнозирования позиций небесных светил в небе, и мог служить также как планетарий для демонстрации их движения. Таким образом, речь идет о более сложном и многофункциональном устройстве, чем небесный глобус Архимеда.
Плохая сохранность и фрагментарность дошедших до нас частей Антикитерского механизма делают любую попытку его реконструкции гипотетической. Тем не менее, благодаря кропотливой работе исследователей, мы можем с достаточной уверенностью представить, хотя бы в общих чертах, его устройство и функции.
После установки даты прибор, предположительно, приводили в действие вращением ручки, расположенной на боковой грани корпуса. Большое ведущее колесо с 4 спицами (фото 3) было связано с помощью многоступенчатых зубчатых передач с многочисленными шестеренками, вращавшимися с различной скоростью и, в конечном итоге, перемещавшими указатели на циферблатах.
Механизм имел три основных циферблата с концентрическими шкалами: один на передней панели и два на задней панели. На передней панели имелось две шкалы: неподвижная внешняя, представляющая эклиптику (большой круг небесной сферы, по которому происходит видимое годичное движение Солнца), разделенная на 360 градусов и на 12 отрезков по 30 градусов со знаками Зодиака, и подвижная внутренняя, имевшая 365 делений по числу дней в египетском календаре, использовавшемся греческими астрономами. Погрешность календаря, вызванная большей реальной продолжительностью солнечного года (365,2422 дней), могла корректироваться поворотом календарного циферблата на 1 деление назад за каждые 4 года. (Следует отметить, что юлианский календарь, содержащий дополнительный день в високосные годы, был введен только в 46 г. до н.э.).
Передний циферблат имел, вероятно, по крайней мере, три стрелочных индикатора: один с указанием даты, а два других с указанием положений Солнца и Луны относительно плоскости эклиптики.
Указатель положения Луны позволял учитывать особенности ее движения, открытые Гиппархом. Гиппарх нашел, что лунная орбита представляет собой эллипс, наклоненный на 5 градусов к плоскости земной орбиты. Луна движется по эклиптике быстрее вблизи перигея и медленнее в апогее, что в хорошем приближении следует второму закону Кеплера для угловой скорости. Чтобы учесть эту неравномерность, использовалась хитроумная система зубчатых передач, включавшая две шестеренки со смещенным относительно оси вращения центром тяжести.
Логично предположить, что имелся аналогичный механизм, показывающий движение Солнца в соответствии с теорией Гиппарха, однако передача этого механизма (если он существовал) была утрачена.
На передней панели располагался также механизм с индикатором фаз Луны. Сферическая модель Луны, наполовину посеребренная, наполовину черная, показывалась в круглом окошке, демонстрируя текущую фазу Луны.
Существует точка зрения, что механизм мог иметь указатели для всех пяти планет, известных грекам (это Меркурий, Венера, Марс, Юпитер и Сатурн). Но ни одна передача, отвечающая за такие планетарные механизмы, не найдена, за исключением одной системы передач (фрагмент D), назначение которой неясно. В то же время недавно обнаруженные надписи, в которых упоминаются стационарные точки планет, позволяют предположить, что Антикитерский механизм мог также описывать их движение.
Фото 8. Зодиакальная шкала, календарная шкала и парапегма
Фото 9. Фрагмент текста парапегмы
Таким образом, прибор мог показывать взаимное расположение светил на небесной сфере на конкретную дату, что могло иметь практическое применение в работе астрономов и астрологов (астрология широко практиковалась в Древнем мире), избавляя от сложных и трудоемких расчетов.
Однако в 2008 году руководитель Проекта по исследованию Антикитерского механизма Тони Фриз и его коллеги обнаружили на этом циферблате названия 4 панэллинских игр (Истмийских, Олимпийских, Немейских и Пифийских), а также игр в Додоне. Олимпийский циферблат должен быть включен в существующую зубчатую передачу, перемещавшую указатель на 1/4 оборота за год.
Это подтверждает, что Антикитерский механизм мог использоваться для расчетов дат религиозных праздников, связанных с астрономическими событиями (в том числе Олимпийских и других священных игр), а также служить для коррекции календарей на основе Метонова цикла. Это имело важное практическое значение в Греции, где почти каждый полис имел собственный гражданский календарь, что создавало невероятную путаницу.

На шкале циферблата, показывающего цикл Сарос, имеются символы Σ для лунных затмений (ΣΕΛΗΝΗ, Луна) и Η для солнечных затмений (ΗΛΙΟΣ, Солнце) и цифровые обозначения, выполненные греческими буквами, предположительно указывавшие на дату и час затмений. Удалось установить корреляции с реально наблюдавшимися затмениями.
Это подтверждает, что прибор мог использоваться для прогнозирования лунных и, возможно, солнечных затмений.
Антикитерский механизм был заключен в деревянный ящик, на дверцах которого находились бронзовые таблички, содержащие руководство по его применению с астрономическими, механическими и географическими данными. Интересно, что среди географических названий в тексте встречается ΙΣΠΑΝΙΑ (Испания по-гречески), что является старейшим упоминанием страны в этой форме, в отличие от Иберии.
Рентгеновское изображение (слева) и компьютерная модель (справа) блока, ответственного за моделирование обращения Луны (фото T. Freeth et al.).
«Это устройство просто экстраординарное, оно единственное в своём роде, — говорит Майк Эдмундс (Mike Edmunds), профессор из университета Кардиффа (Cardiff University), возглавляющий исследование механизма. – Его дизайн превосходен, и астрономия совершенно точна… С точки зрения исторической ценности этот механизм я считаю дороже Моны Лизы».
В новой работе учёные использовали точные рентгеновские сканеры для реконструкции строения шестерёнок, а также для распознавания почти стёртых надписей на поверхности устройства.
Как показал тщательный анализ, проведённый с помощью этой современной аппаратуры, на солнечном календаре, на передней панели механизма были указатели для Солнца и Луны под названиями «золотая маленькая сфера» и просто «маленькая сфера» соответственно. Кроме того, обнаружились отметки, устанавливавшие соответствие между зодиаком и солнечным календарём.
Что касается другого солнечного календаря на обратной стороне механизма, то удалось выяснить, что он использовался для предсказания солнечных и лунных затмений.
Также исследователи смогли на этот раз узнать, что это устройство даже учитывало неравномерность движения Луны, вызванную тем, что наш спутник обращается не по круговой, а по эллиптической орбите. Для этого авторы антикитерского чуда сделали «лунную» шестерёнку со смещённым центром вращения.
На этот раз получилось уточнить датировку механизма. По данным радиоуглеродного анализа получалось, что эту штуковину изготовили около 65 года до нашей эры. Но как следует из надписей, которые учёные смогли прочитать благодаря рентгеновской аппаратуре, прибор несколько старше – его создали в 150-100 году до нашей эры.
Кстати, с надписями исследователи поработали особенно успешно. Раньше считалось, что распознано 95% текста, тогда как новое исследование добавило к этому знанию не 5%, а почти удвоило его! Это знание оказалось очень ценным – благодаря новым надписям учёные смогли подтвердить представление о том, что механизм помимо упомянутых объектов мог вычислять конфигурации Марса, Юпитера и Сатурна, в чём специалисты раньше сомневались.
Также в реконструкции, сделанной исследователями, 37 колёс, хотя у механизма, хранящемся в афинском Национальном археологическом музее (National Archaeological Museum of Athens), всего 30 деталей, остальные 7 – просто «гипотетические».
«Из-за фрагментарности находки такие предположения неизбежны. Однако с ними новая модель выглядит очень убедительно», — считает Франсуа Шарет (François Charette), исследователь из университета Людвига–Максимилиана (Ludwig-Maximilians-Universität), не принимавший участия в исследовании.
В международной исследовательской команде собрались эксперты по разным отраслям научного знания: астрономы, математики, компьютерщики, археологи и другие. Специалисты, по информационным технологиям, кстати, назвали антикитерский механизм аналоговым компьютером.
И хотя учёные располагают нерабочим экземпляром прибора, они планируют сделать его точную компьютерную модель, а также работающую копию.

Антикитерский механизм, вероятно, был создан во второй половине II века до н.э. Это время расцвета эллинистической астрономии, связанного с именами таких ученых, как Посидоний и Гиппарх.
Гиппархом Никейским был составлен каталог звездного неба, впоследствии использованный Птолемеем, открыта прецессия равноденствий, достаточно точно описаны видимые движения Луны, Солнца и пяти известных тогда планет, определено расстояние от Земли до Луны и размеры последней, очень близкие действительным. Найденное Гиппархом значение синодического месяца всего на 0,5 секунды меньше принимаемого сегодня. Теория Гиппарха позволяла предсказывать лунные затмения с точностью до одного-двух часов и, хотя и с меньшей точностью, солнечные затмения.
Посидоний произвел вычисление расстояния от Земли до Солнца, составившее 5/8 действительного (фантастический результат для того времени).
Веком раньше творил Аристарх Самосский, создатель первой в истории гелиоцентрической системы (на 1800 лет раньше Коперника), и его младший современник Архимед, величайший ученый античного мира и предтеча науки Нового времени.

Многие достижения античной науки казались бы сегодня невероятными, не будь они зафиксированы в дошедших до нас трудах древних ученых. При всей сложности Антикитерского механизма, не имеющей аналогов до Нового времени, он, как представляется, построен на базе астрономических и математических теорий, разработанных греческими учеными к 150-100 г. до н.э. Так что для его трактовки нам не нужно обращаться к Deus ex machina.
Современные исследователи, занятые реконструкцией Антикитерского механизма, сходятся в том, что он, скорее всего, был уникальным устройством. Однако есть близкие по времени свидетельства Цицерона о механических планетариях Архимеда и Посидония. Это позволяет предположить, что существовала древнегреческая традиция создания сложных механизмов, которая впоследствии была передана Византии и исламскому миру, где аналогичные сложные механические устройства были построены мусульманскими инженерами и астрономами в Средние века. Эти устройства были гораздо проще, чем Антикитерский механизм, но они имеют так много точек соприкосновения, что кажется очевидным, что они пришли из общей традиции.
Став жертвой стихии и людской алчности, Антикитерский механизм на две тысячи лет выпал из научного оборота. Но благодаря тому же несчастному случаю, обернувшемуся счастливой случайностью, он сохранился до наших дней и попал в руки современных исследователей, заставив пересмотреть многие из наших оценок античной науки и техники.
А вот еще вам несколько загадок древности: Чье лицо у Сфинкса ? или вот еще - Террасы Морай (Cusco Moray)
Читайте также:


