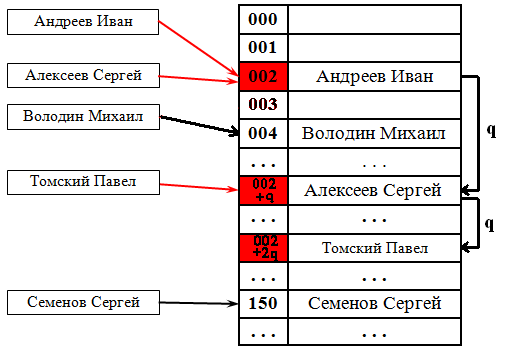
Что такое двойное хеширование
Хеш-таблица - структура данных , реализующая интерфейс ассоциативного массива, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу. По сути это ассоциативный массив, в котором ключ представлен в виде хеш-функции.
Изначально дано множество из ключей и хеш-функция, которая отображает множество ключей в множество хешей. Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Вычисленное значение играет роль индекса в массиве, которым фактически и является хеш-таблица. Естественной проблемой хеш-таблиц является неинъективность хеш-функции, что ведет к возникновению коллизий(см. Рисунок 1).
Определение «Коллизия»Коллизией назовем ситуацию, при которой значения хеш-функции на двух или более различных ключах совпадают
Таким образом, мы сталкиваемся с проблемой, так как в одной ячейке массива не может храниться более 1 элемента. Проблема коллизий является основной проблемой в реализации данной структуры данных, вопросы связанные с этой проблемой будут затронуты дальше, пока что предлагаем ознакомиться с примером хеш-таблицы:
Пример Пример 1- хеш-таблица
Вероятности коллизии
Пример Пример 2- вероятность коллизий для примера 1Разрешение коллизий
С коллизиями можно и нужно бороться. Существует несколько способов разрешения коллизий: [Источник 2]
Метод цепочек

Для подсчета вычислительной сложности основных операций взаимодействия с хеш-таблицей введем следующее определение.
Определение «Коэффициент заполнения таблицы»Открытая адресация
В массиве H хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива H в некотором порядке до тех пор, пока не будет найдена первая свободная ячейка, в которую и будет записан новый элемент(см.Рисунок 3). Этот порядок вычисляется на лету, что позволяет сэкономить на памяти для указателей, требующихся в хеш-таблицах с цепочками.
Алгоритм поиска просматривает ячейки хеш-таблицы в том же самом порядке, что и при вставке, до тех пор, пока не найдется либо элемент с искомым ключом, либо свободная ячейка (что означает отсутствие элемента в хеш-таблице). Удаление элементов в такой схеме несколько затруднено. Обычно поступают так: заводят булевый флаг для каждой ячейки, помечающий, удален элемент в ней или нет. Тогда удаление элемента состоит в установке этого флага для соответствующей ячейки хеш-таблицы, но при этом необходимо модифицировать процедуру поиска существующего элемента так, чтобы она считала удалённые ячейки занятыми, а процедуру добавления — чтобы она их считала свободными и сбрасывала значение флага при добавлении.

Основные типы последовательностей проб
Ниже приведены некоторые распространенные типы последовательностей проб. [Источник 3]
Линейное пробирование
Определение «Линейное пробирование»Линейным пробированием называется метод разрешения коллизий в хеш-таблице с открытой адресацией, при котором i-ый элемент последовательности проб это h a s h ( x ) + i k m o d n , где n - размер таблицы, k - некоторая фиксированная константа.
Утверждение Об ограничениях на k Пример Пример 3- линейное пробированиеПоиск элемента в таблице осуществляется аналогично добавлению: мы проверяем ячейку i и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку. Аналогично реализовано удаление.
Квадратичное пробирование
Определение «Квадратичное пробирование»Выполнение всех основных операции в хеш-таблице с квадратичной последовательностью проб совпадает с их реализацией при линейном пробировании.
Двойное хеширование
Определение «Двойное хеширование»Двойным хешированием называется метод разрешения коллизий в хеш-таблице с открытой адресацией, при котором интервал между ячейками фиксирован, как при линейном пробировании, но, в отличие от него, размер интервала вычисляется второй, вспомогательной хеш-функцией, а значит, может быть различным для разных ключей.
Заключение
Наиболее важным свойством хеш-таблицы является то, что, при некоторых разумных допущениях, все три операции (поиск, вставка, удаление элементов) в среднем выполняются за время O ( 1 ) . Но при этом не гарантируется, что время выполнения отдельной операции мало.
Я много раз заглядывал на просторы интернета, нашел много интересных статей о хеш-таблицах, но вразумительного и полного описания того, как они реализованы, так и не нашел. В связи с этим мне просто нетерпелось написать пост на данную, столь интересную, тему.
Возможно, она не столь полезна для опытных программистов, но будет интересна для студентов технических ВУЗов и начинающих программистов-самоучек.

Мотивация использовать хеш-таблицы
Для наглядности рассмотрим стандартные контейнеры и асимптотику их наиболее часто используемых методов.
| Контейнер \ операция | insert | remove | find |
|---|---|---|---|
| Array | O(N) | O(N) | O(N) |
| List | O(1) | O(1) | O(N) |
| Sorted array | O(N) | O(N) | O(logN) |
| Бинарное дерево поиска | O(logN) | O(logN) | O(logN) |
| Хеш-таблица | O(1) | O(1) | O(1) |
Все данные при условии хорошо выполненных контейнерах, хорошо подобранных хеш-функциях
Из этой таблицы очень хорошо понятно, почему же стоит использовать хеш-таблицы. Но тогда возникает противоположный вопрос: почему же тогда ими не пользуются постоянно?
Ответ очень прост: как и всегда, невозможно получить все сразу, а именно: и скорость, и память. Хеш-таблицы тяжеловесные, и, хоть они и быстро отвечают на вопросы основных операций, пользоваться ими все время очень затратно.
Понятие хеш-таблицы
Хеш-таблица — это контейнер, который используют, если хотят быстро выполнять операции вставки/удаления/нахождения. В языке C++ хеш-таблицы скрываются под флагом unoredered_set и unordered_map. В Python вы можете использовать стандартную коллекцию set — это тоже хеш-таблица.
Реализация у нее, возможно, и не очевидная, но довольно простая, а главное — как же круто использовать хеш-таблицы, а для этого лучше научиться, как они устроены.
Для начала объяснение в нескольких словах. Мы определяем функцию хеширования, которая по каждому входящему элементу будет определять натуральное число. А уже дальше по этому натуральному числу мы будем класть элемент в (допустим) массив. Тогда имея такую функцию мы можем за O(1) обработать элемент.
Теперь стало понятно, почему же это именно хеш-таблица.
Проблема коллизии
Естественно, возникает вопрос, почему невозможно такое, что мы попадем дважды в одну ячейку массива, ведь представить функцию, которая ставит в сравнение каждому элементу совершенно различные натуральные числа просто невозможно. Именно так возникает проблема коллизии, или проблемы, когда хеш-функция выдает одинаковое натуральное число для разных элементов.
Существует несколько решений данной проблемы: метод цепочек и метод двойного хеширования. В данной статье я постараюсь рассказать о втором методе, как о более красивом и, возможно, более сложном.
Решения проблемы коллизии методом двойного хеширования
Мы будем (как несложно догадаться из названия) использовать две хеш-функции, возвращающие взаимопростые натуральные числа.
Одна хеш-функция (при входе g) будет возвращать натуральное число s, которое будет для нас начальным. То есть первое, что мы сделаем, попробуем поставить элемент g на позицию s в нашем массиве. Но что, если это место уже занято? Именно здесь нам пригодится вторая хеш-функция, которая будет возвращать t — шаг, с которым мы будем в дальнейшем искать место, куда бы поставить элемент g.
Мы будем рассматривать сначала элемент s, потом s + t, затем s + 2*t и т.д. Естественно, чтобы не выйти за границы массива, мы обязаны смотреть на номер элемента по модулю (остатку от деления на размер массива).
Наконец мы объяснили все самые важные моменты, можно перейти к непосредственному написанию кода, где уже можно будет рассмотреть все оставшиеся нюансы. Ну а строгое математическое доказательство корректности использования двойного хеширования можно найти тут.
Для наглядности будем реализовывать хеш-таблицу, хранящую строки.
Начнем с определения самих хеш-функций, реализуем их методом Горнера. Важным параметром корректности хеш-функции является то, что возвращаемое значение должно быть взаимопросто с размером таблицы. Для уменьшения дублирования кода, будем использовать две структуры, ссылающиеся на реализацию самой хеш-функции.
Чтобы идти дальше, нам необходимо разобраться с проблемой: что же будет, если мы удалим элемент из таблицы? Так вот, его нужно пометить флагом deleted, но просто удалять его безвозвратно нельзя. Ведь если мы так сделаем, то при попытке найти элемент (значение хеш-функции которого совпадет с ее значением у нашего удаленного элемента) мы сразу наткнемся на пустую ячейку. А это значит, что такого элемента и не было никогда, хотя, он лежит, просто где-то дальше в массиве. Это основная сложность использования данного метода решения коллизий.
Помня о данной проблеме построим наш класс.
На данном этапе мы уже более-менее поняли, что у нас будет храниться в таблице. Переходим к реализации служебных методов.
Из необходимых методов осталось еще реализовать динамическое увеличение, расширение массива — метод Resize.
Увеличиваем размер мы стандартно вдвое.
Немаловажным является поддержание асимптотики O(1) стандартных операций. Но что же может повлиять на скорость работы? Наши удаленные элементы (deleted). Ведь, как мы помним, мы ничего не можем с ними сделать, но и окончательно обнулить их не можем. Так что они тянутся за нами огромным балластом. Для ускорения работы нашей хеш-таблицы воспользуемся рехешом (как мы помним, мы уже выделяли под это очень странные переменные).
Теперь воспользуемся ими, если процент реальных элементов массива стал меньше 50, мы производим Rehash, а именно делаем то же самое, что и при увеличении таблицы (resize), но не увеличиваем. Возможно, это звучит глуповато, но попробую сейчас объяснить. Мы вызовем наши хеш-функции от всех элементов, переместим их в новых массив. Но с deleted-элементами это не произойдет, мы не будем их перемещать, и они удалятся вместе со старой таблицей.
Но к чему слова, код все разъяснит:
Ну теперь мы уже точно на финальной, хоть и длинной, и полной колючих кустарников, прямой. Нам необходимо реализовать вставку (Add), удаление (Remove) и поиск (Find) элемента.
Начнем с самого простого — метод Find элемент по значению.
Далее мы реализуем удаление элемента — Remove. Как мы это делаем? Находим элемент (как в методе Find), а затем удаляем, то есть просто меняем значение state на false, но сам Node мы не удаляем.
Ну и последним мы реализуем метод Add. В нем есть несколько очень важных нюансов. Именно здесь мы будем проверять на необходимость рехеша.
Помимо этого в данном методе есть еще одна часть, поддерживающая правильную асимптотику. Это запоминание первого подходящего для вставки элемента (даже если он deleted). Именно туда мы вставим элемент, если в нашей хеш-таблицы нет такого же. Если ни одного deleted-элемента на нашем пути нет, мы создаем новый Node с нашим вставляемым значением.
Разрешение коллизий (англ. collision resolution) в хеш-таблице, задача, решаемая несколькими способами: метод цепочек, открытая адресация и т.д. Очень важно сводить количество коллизий к минимуму, так как это увеличивает время работы с хеш-таблицами.
Содержание

Каждая ячейка [math]i[/math] массива [math]H[/math] содержит указатель на начало списка всех элементов, хеш-код которых равен [math]i[/math] , либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.
В зависимости от того нужна ли нам уникальность значений операции вставки у нас будет работать за разное время. Если не важна, то мы используем список, время вставки в который будет в худшем случае равна [math]O(1)[/math] . Иначе мы проверяем есть ли в списке данный элемент, а потом в случае его отсутствия мы его добавляем. В таком случае вставка элемента в худшем случае будет выполнена за [math]O(n)[/math]
Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math] ) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.
Удаления элемента может быть выполнено за [math]O(1)[/math] , как и вставка, при использовании двухсвязного списка.

Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.
Последовательный поиск
При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+1, i+2, i+3[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.

Линейный поиск
Выбираем шаг [math]q[/math] . При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск - частный случай линейного, где [math]q=1[/math] .
Квадратичный поиск
Шаг [math]q[/math] не фиксирован, а изменяется квадратично: [math]q = 1,4,9,16. [/math] . Соответственно при попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math] i+1, i+4, i+9[/math] и так далее, пока не найдём свободную ячейку.

Проверка осуществляется аналогично добавлению: мы проверяем ячейку [math]i[/math] и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.
При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.
Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.
Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.
Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на [math]q[/math] позиций назад. При этом:
- если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
- в цепочке не должно оставаться "дырок", тогда любой элемент с данным хешем будет доступен из начала цепи
Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).
Хеш-таблицу считаем зацикленной
Асимптотически время работы [math]\mathrmВариант с зацикливанием мы не рассматриваем, поскольку если [math]q[/math] взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций
Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.
Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце [math]\mathrm[/math] (см. псевдокод) заметёт созданную дыру (скопированный элемент), и сам, по предположению, новых не создаст.
- Элементы, которые уже на своих местах, не должны быть сдвинуты.
Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на [math]q[/math] позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.
Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.
При двойном хешировании используются две независимые хеш-функции [math] h_1(k) [/math] и [math] h_2(k) [/math] . Пусть [math] k [/math] — это наш ключ, [math] m [/math] — размер нашей таблицы, [math]n \bmod m [/math] — остаток от деления [math] n [/math] на [math] m [/math] , тогда сначала исследуется ячейка с адресом [math] h_1(k) [/math] , если она уже занята, то рассматривается [math] (h_1(k) + h_2(k)) \bmod m [/math] , затем [math] (h_1(k) + 2 \cdot h_2(k)) \bmod m [/math] и так далее. В общем случае идёт проверка последовательности ячеек [math] (h_1(k) + i \cdot h_2(k)) \bmod m [/math] где [math] i = (0, 1, \; . \;, m - 1) [/math]
Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за [math]O(1)[/math] , в худшем — за [math]O(m)[/math] , что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.
[math]\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))[/math]
[math] h_1 [/math] может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, [math] h_2 [/math] должна возвращать значения:
- не равные [math] 0 [/math]
- независимые от [math] h_1 [/math]
- взаимно простые с величиной хеш-таблицы
Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а [math] h_2 [/math] возвращает натуральные числа, меньшие [math] m [/math] . Второй — размер таблицы является степенью двойки, а [math] h_2 [/math] возвращает нечетные значения.
Например, если размер таблицы равен [math] m [/math] , то в качестве [math] h_2 [/math] можно использовать функцию вида [math] h_2(k) = k \bmod (m-1) + 1 [/math]
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:
[math] h(k,i) = (h_1(k) + i \cdot h_2(k)) \bmod 13 [/math]
[math] h_1(k) = k \bmod 13 [/math]
[math] h_2(k) = 1 + k \bmod 11 [/math]
Мы хотим вставить ключ 14. Изначально [math] i = 0 [/math] . Тогда [math] h(14,0) = (h_1(14) + 0\cdot h_2(14)) \bmod 13 = 1 [/math] . Но ячейка с индексом 1 занята, поэтому увеличиваем [math] i [/math] на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При [math] i = 2 [/math] получаем [math] h(14,2) = (h_1(14) + 2\cdot h_2(14)) \bmod 13 = 9 [/math] . Ячейка с номером 9 свободна, значит записываем туда наш ключ.
Таким образом, основная особенность двойного хеширования состоит в том, что при различных [math] k [/math] пара [math] (h_1(k),h_2(k)) [/math] дает различные последовательности ячеек для исследования.
Пусть у нас есть некоторый объект [math] item [/math] , в котором определено поле [math] key [/math] , от которого можно вычислить хеш-функции [math] h_1(key)[/math] и [math] h_2(key) [/math]
Так же у нас есть таблица [math] table [/math] величиной [math] m [/math] , состоящая из объектов типа [math] item [/math] .
Чтобы наша хеш-таблица поддерживала удаление, требуется добавить массив [math]deleted[/math] типов [math]bool[/math] , равный по величине массиву [math]table[/math] . Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.
В Java 8 для разрешения коллизий используется модифицированный метод цепочек. Суть его заключается в том, что когда количество элементов в корзине превышает определенное значение, данная корзина переходит от использования связного списка к использованию сбалансированного дерева. Но данный метод имеет смысл лишь тогда, когда на элементах хеш-таблицы задан линейный порядок. То есть при использовании данный типа [math]\mathbf[/math] или [math]\mathbf[/math] имеет смысл переходить к дереву поиска, а при использовании каких-нибудь ссылок на объекты не имеет, так как они не реализуют нужный интерфейс. Такой подход позволяет улучшить производительность с [math]O(n)[/math] до [math]O(\log(n))[/math] . Данный способ используется в таких коллекциях как HashMap, LinkedHashMap и ConcurrentHashMap.
Основной принцип линейного опробования (а, вообще-то, и любого метода хеширования) —гарантирование того, что при поиске конкретного ключа мы просматриваем каждый ключ, который отображается в тот же адрес в таблице (в частности, сам ключ, если он есть в таблице). Однако при использовании схемы с открытой адресацией, как правило, просматриваются и другие ключи, особенно когда заполнение таблицы велико. В примере, приведенном на рис. 14.7, при поиске ключа N просматриваются ключи C, E, R и I, ни один из которых не имеет такого же хеш-значения. Что еще хуже, вставка ключа с одним хеш-значением может существенно увеличить время поиска ключей с другими хеш-значениями: на рис. 14.7 вставка ключа M приводит к увеличению времени поиска для позиций 7-12 и 0-1. Это явление называется кластеризацией (clustering), поскольку оно связано с процессом образования кластеров. Для почти заполненных таблиц оно может значительно замедлять линейное опробование.
К счастью, существует простой способ избежать возникновения проблемы кластеризации — двойное хеширование (double hashing). Основная стратегия остается той же, что и при выполнении линейного опробования; единственное различие состоит в том, что вместо просмотра каждой позиции таблицы, следующей за коллизией, мы используем вторую хеш-функцию для получения постоянного шага, используемого для последовательных проб. Реализация этого способа приведена в программе 14.6.
Программа 14.6. Двойное хеширование
Двойное хеширование аналогично линейному опробованию, за исключением того, что здесь используется вторая хеш-функция — для определения шага поиска, используемого после каждой коллизии. Шаг поиска должен быть ненулевым, а размер таблицы и шаг поиска должны быть взаимно простыми числами. Функция remove для линейного опробования (см. программу 14.5) не работает с двойным хешированием, поскольку любой ключ может присутствовать во многих различных последовательностях проб.
Выбор второй хеш-функции требует определенной осторожности, поскольку в противном случае программа может вообще не работать. Во-первых, необходимо исключить случай, когда вторая хеш-функция дает нулевое значение, поскольку при первой же коллизии это приведет к бесконечному циклу. Во-вторых, важно, чтобы значение второй хеш-функции и размер таблицы были взаимно простыми числами, т.к. иначе некоторые из последовательностей проб могут оказаться очень короткими (например, в случае, когда размер таблицы вдвое больше значения второй хеш-функции). Один из способов претворения этих правил в жизнь — выбор в качестве M простого числа и выбор второй хеш-функции, возвращающей значения, меньшие M. На практике во многих ситуациях, если размер таблицы не слишком мал, будет достаточно простой второй хеш-функции вроде
Кроме того, любое снижение эффективности (из-за уменьшения дисперсии), вызываемое данным упрощением, на практике, скорее всего, будет не только не важно, но и вовсе незаметно. Если таблица большая и разреженная, сам размер таблицы не обязательно должен быть простым числом, поскольку для каждого поиска нужно будет лишь несколько проб (хотя было бы неплохо для предотвращения бесконечного цикла выполнять проверки на длинные последовательности проб и прерывать их — см. упражнение 14.38).
На рис. 14.9 показан процесс построения небольшой таблицы методом двойного хеширования, а из рис. 14.10 видно, что двойное хеширование приводит к образованию значительно меньшего количества кластеров (которые поэтому значительно короче), чем в результате линейного опробования.
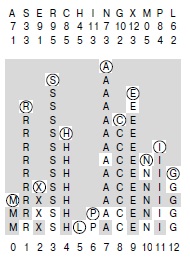
На этой диаграмме показан процесс вставки ключей A S E R C H I N G X M P L в первоначально пустую хеш-таблицу с открытой адресацией с использованием хеш-значений, приведенных вверху, и разрешением коллизий с помощью двойного хеширования. Первое и второе хеш-значения каждого ключа приведены в двух строках под этим ключом. Как и на рис. 14.7, проверяемые позиции таблицы выделены белым цветом. Ключ A попадает в позицию 7, затем S попадает в позицию 3, E — в позицию 9, как и на рис. 14.7. Но ключ R после коллизии в позиции 9 попадает в позицию 1; его второе хеш-значение, равное 5, используется в качестве шага последовательности проб после коллизии. Аналогично, ключ P окончательно попадает в позицию 6 после коллизий в позициях 8, 12, 3, 7, 11 и 2 при использовании в качестве шага его второго хеш-значения, равного 4.
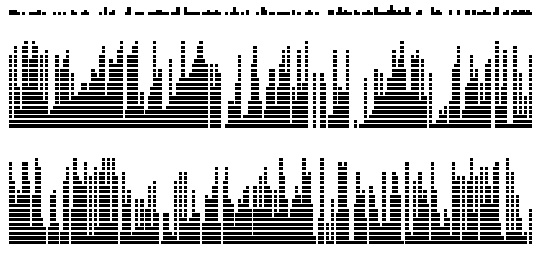
На этих диаграммах показано размещение записей при их вставке в хеш-таблицу с использованием линейного опробования (в центре) и двойного хеширования (внизу), при распределении ключей, показанном на верхней диаграмме. Каждая черточка показывает результат вставки 10 записей. По мере заполнения таблицы записи объединяются в кластеры, разделенные пустыми позициями таблицы. Длинные кластеры нежелательны, т.к. средние затраты на поиск одного ключа в кластере пропорциональны длине кластера. В случае линейного опробования чем длиннее кластеры, тем более вероятно их удлинение, поэтому по мере заполнения таблицы оказываются доминирующими несколько длинных кластеров. При использовании двойного хеширования этот эффект значительно менее выражен, и кластеры остаются сравнительно короткими.
Лемма 14.4. При разрешении коллизий с помощью двойного хеширования среднее количество проб, необходимых для выполнения поиска в хеш-таблице размером M, содержащей ключей, равно \ln\left(\dfrac\right)$" />
и $" />
соответственно для успешного и неудачного поиска.
Эти формулы — результат глубокого математического анализа, выполненного Гиба (Guibas) и Шемереди (Szemeredi) (см. раздел ссылок). Доказательство основывается на том, что двойное хеширование почти эквивалентно более сложному алгоритму случайного хеширования, при котором используется зависящая от ключей последовательность позиций опробования, обеспечивающая равную вероятность попадания каждой пробы в каждую позицию таблицы. Этот алгоритм всего лишь аппроксимирует двойное хеширование, по многим причинам: например, очень трудно гарантировать, что при двойном хешировании каждая позиция таблицы проверяется хотя бы один раз, но при случайном хешировании одна и та же позиция таблицы может проверяться и более одного раза.
Однако для разреженных таблиц вероятность возникновения коллизий при использовании обоих методов одинакова. Интерес представляют оба метода: двойное хеширование легко реализовать, а случайное хеширование легко анализировать.
При случайном хешировании средние затраты на неудачный поиск определяются равенством

Выражение слева — сумма вероятностей, что при неудачном поиске используются более к проб, при к = 0, 1, 2, . (на основании элементарной теории вероятностей она равна средней вероятности). При поиске всегда используется одна проба, затем с вероятностью N/M требуется вторая проба, с вероятностью (N/M) 2 — третья проба и т.д. Эту же формулу можно использовать для вычисления следующего приближенного значения средней стоимости успешного поиска в таблице, содержащей N ключей:

Вероятность успешного поиска одинакова для всех ключей в таблице; затраты на отыскание ключа равны затратам на его вставку, а затраты на вставку j-го ключа в таблицу равны затратам на неудачный поиск в таблице, содержащей j — 1 ключ, поэтому данная формула определяет среднее значение этих затрат.
Теперь эту сумму можно упростить и вычислить, умножив числители и знаменатели всех дробей на M:


поскольку \approx \ln$" />
.
Точная природа взаимосвязи между производительностью двойного хеширования и идеальным случаем случайного хеширования, установленной Гиба и Шемереди — асимптотическое приближение, которое не обязательно должно быть справедливо для используемых на практике размеров таблиц. Кроме того, полученные результаты основываются на предположении, что хеш-функции возвращают случайные значения. Но все же асимптотические формулы из свойства 14.5 на практике позволяют достаточно точно предсказать производительность двойного хеширования, даже при использовании такой просто вычисляемой второй хеш-функции, как (v % 97)+1 . Как и соответствующие формулы для линейного опробования, при приближении значения а к 1 эти формулы стремятся к бесконечности, но гораздо медленнее.
Различие между линейным опробованием и двойным хешированием хорошо видно на рис. 14.11. В разреженных таблицах двойное хеширование и линейное опробование имеют схожую производительность, но при использовании двойного хеширования можно допустить значительно большую степень заполнения таблицы, чем при использовании линейного опробования, прежде чем производительность заметно снизится. В следующей таблице приведено ожидаемое количество проб для успешного и неудачного поиска при использовании двойного хеширования:
Неудачный поиск всегда требует больших затрат, чем успешный, но и тому, и другому в среднем требуется лишь несколько проб, даже в таблице, заполненной на девять десятых.
Можно взглянуть на эти результаты и под другим углом: для получения такого же среднего времени поиска двойное хеширование позволяет использовать меньшие таблицы, чем нужно при использовании линейного опробования.

Рис. 14.11. Затраты на выполнение поиска с открытой адресацией
На этих графиках показаны затраты на построение хеш-таблицы размером 1000 вставками ключей в первоначально пустую таблицу с помощью линейного опробования (вверху) и двойного хеширования (внизу). Каждый вертикальный столбец представляет затраты на вставку 20 ключей. Серые кривые — теоретически предсказанные затраты (см. леммы 14.4 и 14.5).
Лемма 14.5. Сохраняя коэффициент загрузки меньшим, чем $" />
для линейного опробования и меньшим, чем для двойного хеширования, можно обеспечить, что в среднем для выполнения всех поисков потребуется меньше t проб.
Установите значения выражений для неудачного поиска в свойствах 14.4 и 14.5 равными t и решите уравнения относительно .
Например, чтобы среднее количество проб при поиске было меньшим 10, при использовании линейного опробования необходимо сохранять таблицу пустой не менее чем на 32%, а при использовании двойного хеширования — лишь на 10%. Чтобы можно было выполнить неудачный поиск менее чем за 10 проб при обработке 10 5 элементов, нужно свободное место лишь для 10 4 дополнительных элементов. В то же время при использовании цепочек переполнения потребовалась бы дополнительная память для более чем 10 5 ссылок, а при использовании деревьев бинарного поиска — еще вдвое больший объем памяти.
Метод реализации операции удалить, приведенный в программе 14.5 (повторное хеширование ключей, для которых путь поиска может содержать удаляемый элемент), для двойного хеширования не годится, т.к. удаленный элемент может присутствовать во многих различных последовательностях проб для ключей, разбросанных по всей таблице. Поэтому приходится применять другой метод, рассмотренный в конце "Таблицы символов и деревья бинарного поиска" : удаленный элемент заменяется сигнальным элементом, помечающим позицию таблицы как занятую, но не соответствующим ни одному из ключей (см. упражнение 14.33).
Подобно линейному опробованию, двойное хеширование не годится в качестве основы для реализации полнофункционального АТД таблицы символов, в котором необходимо поддерживать операции сортировать или выбрать.
14.31. Приведите содержимое хеш-таблицы, образованной вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустую таблицу размером М = 16 при использовании двойного хеширования. Воспользуйтесь хеш-функцией 11k mod М для первой пробы и второй хеш-функцией (k mod 3) + 1 для шага поиска (если ключ является k-ой буквой алфавита).
14.32. Выполните упражнение 14.31 для М = 10.
14.33. Реализуйте удаление для двойного хеширования с использованием сигнального элемента.
14.34. Измените решение упражнения 14.27, чтобы в нем использовалось двойное хеширование.
14.35. Измените решение упражнения 14.28, чтобы в нем использовалось двойное хеширование.
14.36. Измените решение упражнения 14.29, чтобы в нем использовалось двойное хеширование.
14.37. Реализуйте алгоритм, который аппроксимирует случайное хеширование, используя ключ в качестве исходного значения для встроенного в программу генератора случайных чисел (как в программе 14.2).
14.38. Пусть таблица, размер которой равен 10 6 , заполнена наполовину, причем занятые позиции распределены случайным образом. Оцените вероятность того, что заняты все позиции, индексы которых кратны 100.
14.39. Допустим, что в коде реализации двойного хеширования присутствует ошибка, приводящая к тому, что одна или обе хеш-функции всегда возвращают одно и то же (ненулевое) значение. Опишите, что происходит в каждой из следующих ситуаций: (1) когда ошибочна первая функция, (2) когда ошибочна вторая функция, (3) когда ошибочны обе функции.
Сравнить хэш-таблицы с различными способами разрешения коллизий: метод цепочек, метод двойного хэширования и метод линейного пробирования.
Хеширование – преобразование ключей к числам.
Хеш-таблица – массив ключей с особой логикой, состоящей из: 1. Вычисления хеш-функции, которая преобразует ключ поиска в индекс. 2. Разрешения конфликтов, т.к. два и более различных ключа могут преобразовываться в один и тот же индекс массива. Отношение порядка над ключами не требуется.
Хеш-функция ― преобразование по детерминированному алгоритму входного массива данных произвольной длины (один ключ) в выходную битовую строку фиксированной длины (значение). Результат вычисления хеш-фукнции называют «хешем».
Хеш-функция должна иметь следующие свойства:
- Всегда возвращать один и тот же адрес для одного и того же ключа;
- Не обязательно возвращает разные адреса для разных ключей;
- Использует все адресное пространство с одинаковой вероятностью;
- Быстро вычислять адрес.
Коллизией хеш-функции H называется два различных входных блока данных X и Y таких, что H(x) = H(y) .
Хеш-таблица – структура данных, хранящая ключи в таблице. Индекс ключа вычисляется с помощью хеш-функции. Операции: добавление, удаление, поиск. Пусть хеш-таблица имеет размер M , количество элементов в хеш-таблице – N .
Число хранимых элементов, делённое на размер массива (число возможных значений хеш-функции), называется коэффициентом заполнения хеш-таблицы (load factor). Обозначим его α = N/M .
Этот коэффициент является важным параметром, от которого зависит среднее время выполнения операций.
Парадокс дней рождений. При вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии уже превысит 50 % (если каждый элемент может равновероятно попасть в любую ячейку).
Хеш-таблицы различаются по методу разрешения коллизий. Основные методы разрешения коллизий:
- Метод цепочек.
- Метод открытой адресации.
Каждая ячейка массива является указателем на связный список (цепочку). Коллизии приводят к тому, что появляются цепочки длиной более одного элемента.
- Вычисляем значение хеш-функции добавляемого ключа – h .
- Находим A[h] – указатель на список ключей.
- Вставляем в начало списка (в конец списка дольше). Если запрещено дублировать ключи, то придется просмотреть весь список.
Время работы: В лучшем случае – O(1) . В худшем случае – если не требуется проверять наличие дубля, то O(1) – иначе – O(N)
- Вычисляем значение хеш-функции удаляемого ключа – h .
- Находим A[h] – указатель на список ключей.
- Ищем в списке удаляемый ключ и удаляем его.
Время работы: В лучшем случае – O(1) . В худшем случае – O(N) .
- Вычисляем значение хеш-функции ключа – h .
- Находим A[h] – указатель на список ключей.
- Ищем его в списке.
Время работы: В лучшем случае – O(1) . В худшем случае – O(N) .
Среднее время работы операций поиска, вставки (с проверкой на дубликаты) и удаления в хеш-таблице, реализованной методом цепочек – O(1 + α) , где α – коэффициент заполнения таблицы.
Среднее время работы.
Среднее время работы операций поиска, вставки (с проверкой на дубликаты) и удаления в хеш-таблице, реализованной методом цепочек – O(1 + α), где α – коэффициент заполнения таблицы.
Доказательство. Среднее время работы – математическое ожидание времени работы в зависимости от исходного ключа. Время работы для обработки одного ключа T(k) зависит от длины цепочки и равно 1 + Nh(k) , где Ni – длина i-ой цепочки. Предполагаем, что хеш-функция равномерна, а ключи равновероятны.
Среднее время работы
Метод открытой адресации
Все элементы хранятся непосредственно в массиве. Каждая запись в массиве содержит либо элемент, либо NIL . При поиске элемента систематически проверяем ячейки до тех пор, пока не найдем искомый элемент или не убедимся в его отсутствии.
При поиске элемента систематически проверяем ячейки до тех пор, пока не найдем искомый элемент или не убедимся в его отсутствии.
- Вычисляем значение хеш-функции ключа – h .
- Систематически проверяем ячейки, начиная от A[h] , до тех пор, пока не находим пустую ячейку.
- Помещаем вставляемый ключ в найденную ячейку. В п.2 поиск пустой ячейки выполняется в некоторой последовательности. Такая последовательность называется «последовательностью проб».
Последовательность проб зависит от вставляемого в таблицу ключа. Для определения исследуемых ячеек расширим хеш-функцию, включив в нее номер пробы (от 0 ).
Важно, чтобы для каждого ключа k последовательность проб h(k, 0), h(k, 1), . , h(k, M − 1) представляла собой перестановку множества 0,1, . , M − 1 , чтобы могли быть просмотрены все ячейки таблицы.
Поиск ключа. Исследуется та же последовательность, что и в алгоритме вставки ключа. Если при поиске встречается пустая ячейка, поиск завершается неуспешно, поскольку искомый ключ должен был бы быть вставлен в эту ячейку в последовательности проб, и никак не позже нее.
Удаление ключа. Алгоритм удаления достаточен сложен. Нельзя при удалении ключа из ячейки i просто пометить ее значением NIL . Иначе в последовательности проб для некоторого ключа (или некоторых) возникнет пустая ячейка, что приведет к неправильной работе алгоритма поиска. Решение. Помечать удаляемые ячейки спец. значением «Deleted» . Нужно изменить методы поиска и вставки. В методе вставки проверять «Deleted» , вставлять на его место. В методе поиска продолжать поиск при обнаружении «Deleted» .
Вычисление последовательности проб. Желательно, чтобы для различных ключей k последовательность проб h(k, 0), h(k, 1), . , h(k, M − 1) давала большое количество последовательностей- перестановок множества 0,1. , M − 1 .
Обычно используются три метода построения h(k, i) :
- Линейное пробирование.
- Квадратичное пробирование.
- Двойное хеширование.
h(k, i) = (h′(k) + i) mod M
Основная проблема – кластеризация. Последовательность подряд идущих занятых элементов таблицы быстро увеличивается, образуя кластер. Попадание в элемент кластера при добавлении гарантирует «одинаковую прогулку» для различных ключей и проб. Новый элемент будет добавлен в конец кластера, увеличивая его.
h(k, i) = (h1(k) + ih2(k)) mod M.
Требуется, чтобы последовательность проб содержала все индексы 0, .. , M–1 . Для этого все значения h2(k) должны быть взаимно простыми с M .
- M может быть степенью двойки, а h2(k) всегда возвращать нечетные числа.
- M простое, а h2(k) меньше M .
Общее количество последовательностей проб O(M^2) .
| Лучший случай | В среднемю Метод цепочек. | В среднем. Метод открытой адресации. | Худший случай. | |
|---|---|---|---|---|
| Поиск | O(1) | O(1 + a) | O(1 / 1 - a) | O(n) |
| Вставка | O(1) | O(1 + a) | O(1 / 1 - a) | O(n) |
| Удаление | O(1) | O(1 + a) | O(1 / 1 - a) | O(n) |
Хеширование полезно, когда широкий диапазон возможных значений должен быть сохранен в малом объеме памяти, и нужен способ быстрого, практически произвольного доступа. Хэш-таблицы часто применяются в базах данных, и, особенно, в языковых процессорах типа компиляторов и ассемблеров, где они изящно обслуживают таблицы идентификаторов. В таких приложениях, таблица - наилучшая структура данных.
Для запуска необходиа java версии 1.8 и Apache Maven версии 3.5.0. Для компиляции необходимо в корне проекта выполнить команду
А для запуска программы
Оба параметра являются обязательными.
Во время выполнения в консоль будут выведены выполненные команды.
Формат входных данных
Примеры: add 10 20 search 15 print min
Команда print отражает внутреннее строение структуры данных. Для хэш-таблицы с методом цепочек вывод команды print будет иметь следующий вид:
<> - отдельная ячейка массива, в которой храниться список ключей. А для хеш-таблиц с открытой адресацией вывод будет выглядеть так:
Hash table: [ 755 D __ 855 __ 942 __ 346 __ 588 __ 576 ]
__ - пустая ячейка, D - удаленная ячейка.
Формат выходных данных
В выходной файл выводятся результаты исполнения программы.
Команда print должна отражать внутреннее строение структуры данных
Команда search выводит error, в случае, когда значение не было найдено, или значение найденное по ключу в противном случае.
Команда add добавляет значение в таблицу (Ничего не выводит).
Команда delete удаляетя число, или ничего не делает, если значение не было найдено (Ничего не выводит).
Команда min выводит минимальное число в таблице, или empty, если таблица пустая.
Команда max выводит максимальное число в таблице,или empty, если таблица пустая.
Было создано три вида тестов. Одни проверяют корректность работы методов каждой хеш-таблицы, вторые для провеки времени выполнения большого числа операций добавления, поиска и удаления.
1.Юнит тесты, проверящие корректность работы методов каждой хеш-таблицы
Тесты находятся в ./src/test/java/tests/
2.Юнит тесты для провеки времени выполнения большого числа операций добавления, поиска и удаления.
Тесты находятся в ./src/test/java/tests/
3.Файлы с входными данными и правильными ответами.
На вход программе подается два файла.
Заитем выходной файл с результатами исполнения программы сравнивается с файлом в котором находятся правильные ответы
Тесты находятся в ./tests/
Подробное описание тестов
1.Простая проверка всех операций кроме print
2.Проверка корректной работы add, delete(удаление элементов по несушествуюшему ключу) и print
3.Проверка корректной работы add, delete(удаление элементов по сушествуюшему ключу) и print
4.Проверка корректной работы search(поиск элементов по несушествуюшему ключу)
5.Проверка корректной работы search(поиск элементов по сушествуюшему ключу)
Сравнение времени работы
Время работы рачитываем тестом с 1000000 операций каждого типа.
Search time: 354
Delete time: 255
Search time: 281
Delete time: 365
Search time: 273
Delete time: 377
При использовании открытой адресации двойное хеширование обычно превосходит квадратичное пробирование. Единственным исключением является ситуация, в которой доступен большой объем памяти, а данные не расширяются после создания таблицы; в этом случае линейное пробирование несколько проще реализуется, а при использовании коэффициентов нагрузки менее 0,5 не приводит к заметным потерям производительности.
Если количество элементов, которые будут вставляться в хеш-таблицу, неизвестно на момент ее создания, метод цепочек предпочтительнее открытой адресации. Увеличение коэффициента заполнения при открытой адресации приводит к резкому снижению быстродействия, а с методом цепочек быстродействие убывает всего лишь линейно.
Если не уверены — используйте метод цепочек. У него есть свои недостатки — прежде всего необходимость в дополнительном классе связанного списка, но зато если в список будет внесено больше данных, чем ожидалось изначально, реализация по крайней мере не замедлится до полного паралича.
План выполнения домашнего задания
You can’t perform that action at this time.
You signed in with another tab or window. Reload to refresh your session. You signed out in another tab or window. Reload to refresh your session.
Читайте также: