Машина атвуда своими руками
Цель работы: изучение закона прямолинейного ускоренного движения тел под действием сил земного тяготения с помощью машины Атвуда.
Основные теоретические сведения
При движении тела любая его точка описывает в пространстве линию, называемую траекторией. Если траектории всех точек тела представляют прямую, то движение называется прямолинейным. Если модуль скорости тела с течением времени увеличивается или уменьшается, то движение называется соответственно, ускоренным или замедленным. Всякое ускорение есть результат действия на движущееся тело сил со стороны других тел. Если действующие силы не изменяются, то ускорение будет постоянным (движение равноускоренным или равнозамедленным).
Принцип работы лабораторной установки
Схема экспериментальной установки на основе машины Атвуда приведена на рис.2.1
Установка включает: основание, вертикальную стойку, верхний кронштейн, кронштейн для установки фотодатчика, фотодатчик.
На вертикальной стойке 1 крепится легкий блок 2, через который перекинута капроновая нить с двумя основными грузами 3,4 и набором разновесов 5. В верхней части стойки расположен электромагнитный тормоз, предназначенный для фиксации исходного положения грузов. На нижнем кронштейне закреплен фотодатчик 6. На корпусе нижнего кронштейна имеется риска, совпадающая с оптической осью фотодатчика.
Нижний кронштейн имеет возможность свободного перемещения и фиксации на вертикальной стойке. На стойку нанесена миллиметровая шкала, по которой определяют начальное и конечное положение грузов, для удобства шкала имеет визир. Начальное положение определяют по нижнему срезу груза, а конечное – по риске на корпусе нижнего кронштейна.
Машина Атвуда
1 -стойка; 2 - блок; 3,4,5 - грузы; 6 - нижний кронштейн; 6 – фотодатчик.
Миллисекундомер представляет прибор с цифровой индикацией времени.
Основание снабжено тремя регулируемыми опорами и зажимом для фиксации вертикальной стойки. Кронштейн имеет зажим для крепления на вертикальной стойке и элементы фиксации фотодатчика. Установка работает от блока электронного ФМ 1/1.
Принцип работы машины Атвуда заключается в том, что когда на концах нити висят грузы одинаковой массы, то система находится в положении безразличного равновесия. Если на правый груз положить перегрузок (или снять дополнительный груз с левого груза) то система грузов выйдет из состояния равновесия и начнет двигаться.
На рис.2 приведена схема, поясняющая принцип действия машины Атвуда.
Совместим начало системы координат с осью блока и направим ось ОХ вертикально вниз. Обозначим массы грузов М, массу перегрузка - т. Предположим, что блок и нить невесомы, нить нерастяжима, сила трения мала. На каждый из грузов действует сила тяжести и сила натяжения нити

Рис. 2. Схема действия машины Атвуда.
Уравнения движения грузов имеют вид:


(1)
В силу нерастяжимости нити ; при невесомом блоке=Т. В итоге имеем следующую систему уравнений:


(2)

Решив эту систему относительно , получим:

. (3)
Так как при данных M и m ускорение постоянно по величине и направлению, то движение грузов будет равноускоренным. Ускорение направлено вертикально вниз.
При равноускоренном движении с нулевой начальной скоростью справедливо выражение:
или (4)
где S - путь, пройденный телом за время движения t, a - ускорение движения.
Соотношение (4) можно проверить экспериментально разными способами, например, таким:
1. Цель. Экспериментально проверить законы равномерного и равноускоренного движений. Определить ускорение свободного падения, рассчитав предельную относительную погрешность.
2. Схематический рисунок установки.

Рис. 1. Машина Атвуда, где 1,2 — одинаковые грузы на концах нити, m – перегрузок, П – кольцевая платформа
3. Расчётные формулы.

(1),

Где – ускорение тела при движении, H – расстояние между верхней и средней платформами.

(2),
Где M И M – массы тела и перегрузка, соответственно, G – Ускорение свободного падения.

(3),
Где H – расстояние между срежней и нижней платформами.

(4),

Где – искомый коэффициент, X И Y – Соответствующие координаты точек на графике линейной зависимости.

(5),

Где A – стандартное отклонение величины , N – число измерений.

(6),

Где – случайная относительная погрешность.

(7),
Где – случайная относительная погрешность, ,, — абсолютные погрешности (приборные и округления) измерения величин H,H,T.

(8)

(9),

Где – предельная абсолютная погрешность прибора.

(10),
Где P — доверительная вероятность, H – цена деления прибора.
и рассчитываются аналогично.

(11),

Где — полная относительная погрешность косвенных измерений величины G.
2 Учебно-методическое пособие предназначено для студентов всех форм обучения. Содержит краткие сведения по теории и описание порядка выполнения упражнений по изучению законов прямолинейного движения с помощью машины Атвуда. Составители Шестакова Р.Г. доц. канд.хим.наук Лейберт Б. М. доц. канд.техн.наук Рецензент Гусманова Г.М. доц. канд.хим.наук Уфимский государственный нефтяной технический университет 00
4 визир 3 и кронштейн 4 для установки фотодатчика. В верхней части установки закреплен малоинерционный шкив 5 через который перекинута капроновая нить 6 с двумя основными грузами 7 и 8 и электромагнитный тормоз (на рисунке не показан) предназначенный для фиксации исходного положения грузов. Для определения расстояний пройденных грузами на вертикальную стойку нанесена миллиметровая шкала и имеется визир облегчающий точное согласование нижней грани груза с определенным началом пути движения. Кронштейн 4 оснащен фотоэлектрическим датчиком с оптической осью на уровне указателя положения кронштейна; после пересечения ее нижней границей падающего грузика образуется электрический сигнал останавливающий счет времени секундомером и включающий электромагнит. ТЕОРИЯ МЕТОДА. На машине Атвуда изучается движение системы грузов подвешенных на нити перекинутой через блок. Определим величину ускорения системы грузов. На каждый груз будут действовать две силы силы тяжести и натяжения нити под действием которых грузы начнут двигаться (рис. ). Если предположить что нить нерастяжима то ускорения правого и левого грузов будут равны по величине. Если предположить кроме того что блок невесом то натяжения нити будут одинаковы и справа и слева. На основании второго закона Ньютона можно записать: M m M M Mg T m g T () где а ускорение системы Т натяжение нити g ускорение свободного падения. Решение системы уравнений дает величину ускорения x T Mg T (M+m)g Рис.. Система грузов машины Атвуда
5 3 mg () M m Более точное определение ускорения движения системы требует учета весомости блока. Натяжения нити по обе стороны блока при этом будут различными. Написанные уравнения дополняются уравнением моментов определяющим закон вращательного движения блока: M Mg T I m0r T M m M m g T T r (3) где I m0r момент инерции блока имеющего массу m 0 и радиус r - угловое ускорение. Если скольжение нити по блоку исключено то линейное и угловое ускорения связаны уравнением r. Решение этой системы уравнений дает ускорение: mg. M m 0 5m (4) Учет силы трения еще больше уменьшает величину ускорения. Как видно из () система грузов будет двигаться с ускорением меньшим чем ускорение свободного падения. Для определения ускорения воспользуемся законами кинематики прямолинейного равноускоренного движения грузов. При равноускоренном движении зависимость пути от времени задается уравнением 0 S V t 0 t t где V 0 начальная скорость. Если V 0 = 0 то S отсюда при движении с одним перегрузком
6 4 S S. (5) t t Для проверки II закона Ньютона в эксперименте используют два перегрузка массами m и m. В первой части опыта оба перегрузка находятся на правом грузе: M m m M m m M Mg T Решая эту систему уравнений получаем g T m m g. (7) M m m Во второй части опыта меньший перегрузок m перекладывается на левый груз: M m M m g M m M m T g T Решение этой системы уравнений дает значение ускорения а С учетом (5) (7) и (9) получим m m g. (9) M m m m m t ; (0) m m t где t и t время движения грузов в первом и во втором случае. Формула () может служить для определения ускорения свободного падения g. Найденные таким образом значения ускорения свободного падения не совпадают с табличным значением. Это вызывается следующими причинами:. При выводе расчетной формулы не учитывалась сила трения возникающая на оси блока которая составляет заметную долю веса перегрузка.. Не производился также учет весомости блока. Как видно из (4) это приводит к получению заниженных значений ускорения. 3. При измерении времени t кроме случайных ошибок возникают и система- (6) (8)
9 7 ТЕХНИКА БЕЗОПАСНОСТИ. Не включать установку прежде чем полностью не ознакомитесь с описанием прибора.. Перед включением убедитесь в наличии заземления прибора КОНТРОЛЬНЫЕ ВОПРОСЫ. Какие физические величины характеризуют прямолинейное движение?. Какое движение называется равномерным равноускоренным? 3. Сформируйте основные законы динамики поступательного движения. 4. Напишите уравнения второго закона Ньютона для движения каждого груза. 5. Напишите уравнения движения системы с учетом массы блока. 6. Как учтены в уравнениях движения грузов условия невесомости блока и нерастяжимости нити? 7. Что называется ускорением свободного падения? 8. Как зависит ускорение свободного падения от широты местности на поверхности Земли? 9. Как изменяется ускорение свободного падения при удалении от поверхности Земли? СПИСОК ЛИТЕРАТУРЫ. Савельев И.В. Курс общей физики. М.: Наука 977. Т.. С Трофимова Т.И. Курс физики. М.: Высшая школа 994. С. 6-.

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.
Что такое машина Атвуда?
Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.
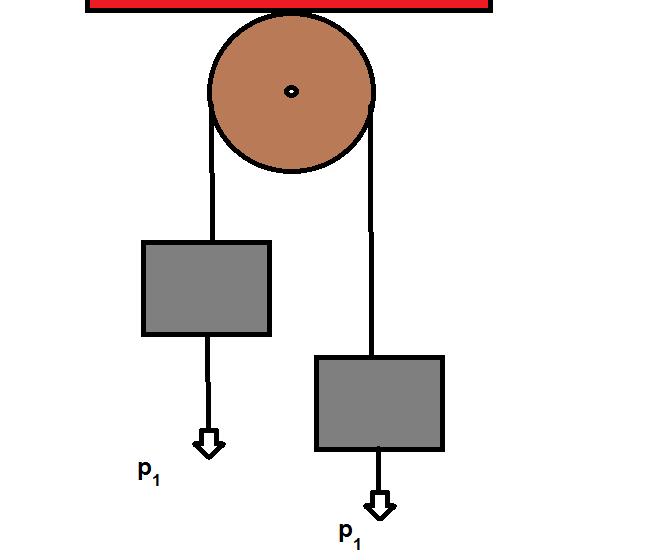
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.
Уравнения динамики
Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:
Где m – инерционная масса тела, a – ускорение.
Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.
Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:
Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:
Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.
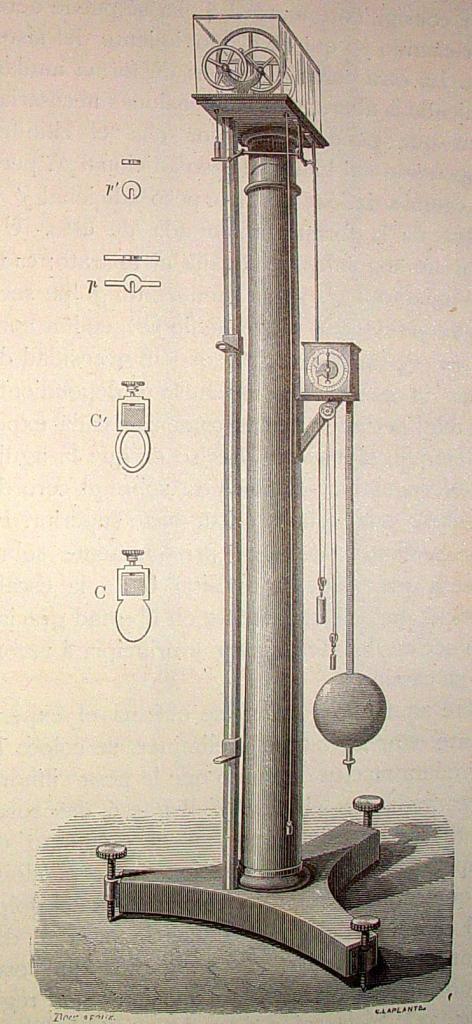
Расчет уравнений динамики для равноускоренного движения
Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.
Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:
Чтобы выразить значение ускорения a, сложим оба равенства, получаем:
Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:
Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:
Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.
Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:
Откуда ускорение определяется однозначно:
Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:
Где m – количество измерений.
Приравнивая это равенство и полученное ранее, приходим к следующему выражению:
Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.
Расчет силы тяжести
Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:
Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:
Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:
Определение силы натяжения нити
Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:
Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:
Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:
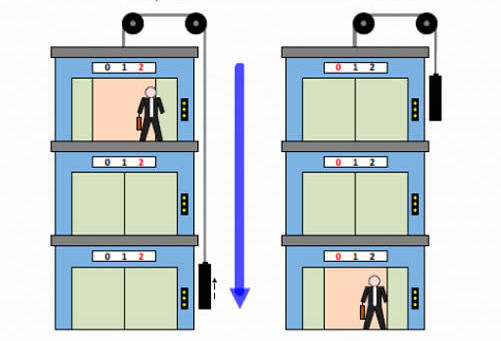
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.
Читайте также:


