На гладком столе расположена система грузов
На горизонтальном столе находится система, состоящая из трёх грузиков массой m каждый и трёх одинаковых пружинок жёсткостью k, соединённых с этими грузиками (см. рис.) Коэффициент трения о стол у двух грузиков — левого и правого — равен а средний грузик может скользить по столу без трения К левому свободному концу самой левой пружинки (точка О) начинают прикладывать горизонтальную силу F, которая очень медленно увеличивается по модулю от нуля до того значения, при котором самый правый грузик начинает скользить по столу. На какое расстояние xО сместится точка О к этому моменту? Известно, что m = 200 г, k = 20 Н/м.
Какие законы Вы использовали для описания движения системы грузов? Обоснуйте их применимость к данному случаю.
Обоснование.
Будем считать систему отсчёта, связанную со столом, инерциальной, грузики — точечными твёрдыми телами, очень медленно движущимися по горизонтальному столу, не опрокидываясь под действием упругих сил со стороны пружинок и сил трения. При таких предположениях можно пользоваться законами статики, а также формулами для сил упругости (законом Гука) и сил сухого трения скольжения и покоя.
Перейдем к решению.
1. Рассмотрим описанную в условии систему в момент перехода самого правого грузика от покоя к скольжению, когда сила его трения о стол Fтр достигает своего максимального значения, равного (сила реакции опоры N = mg, поскольку грузик не движется по вертикали) и направлена влево.
2. Поскольку вся система тел в этот момент не движется, то сумма сил, действующих на неё, как и на каждое из составляющих её тел, по законам статики должна равняться нулю.
3. Правый грузик «толкает» направо деформированная на пружинка с силой Fупр, равной по закону Гука Поскольку сумма сил должна быть равной нулю то получаем откуда
4. По третьему закону Ньютона на эту последнюю пружинку со стороны грузика действует налево сила Fупр, и такая же сила действует направо со стороны «гладкого» грузика.
5. На «гладкий» грузик справа налево действует по третьему закону Ньютона со стороны последней пружинки сила Fупр, и такая же сила действует на него направо со стороны средней пружинки, на которую действует налево та же сила со стороны этого грузика.
6. На среднюю пружинку со стороны первого грузика действует сила Fупр, поэтому она деформирована на ту же величину
7. На первый грузик, который сдвинулся по столу на расстояние для создания деформаций у средней и последней пружинок, действуют налево сила трения о стол Fтр и упругая сила Fупр, в сумме равные которые уравновешиваются упругой силой со стороны первой пружинки:
8. Отсюда деформация первой пружинки равна а расстояние xО, на которое при этом сместилась точка О, складывается из и смещения правого конца этой пружинки, также равного так что
Замечание: задачу можно решить проще, если рассмотреть условие начала движения системы из трёх грузиков и двух пружинок (средней и правой) под действием упругой силы со стороны первой пружинки: для сдвига этой системы нужно преодолеть суммарную силу трения за счёт упругой силы, равной откуда с учётом деформаций по средней и правой пружинок следует ответ, полученный выше:
В обосновании возможности использования законов (закономерностей) допущена ошибка.
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);
II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов);
III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями);
В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.
На гладком столе расположена система грузов
РазделыДополнительно

Задача по физике - 436
На горизонтальной плоскости находятся две одинаковые тонкостенные трубы массой $m$ каждая, оси их параллельны. Вначале одна из труб покоится, а вторая катится без проскальзывания по направлению к первой до столкновения. Скорость поступательного движения трубы равна $\bar
Задача по физике - 437
Горизонтальный стержень OA длины $l$ вращается вокруг вертикальной оси О (рис.). На конце стержня насажено колесо радиуса $r$. Ось колеса горизонтальна и составляет угол $\alpha$ со стержнем OA. Колесо вращается на оси без трения и катится по земле. Трение между колесом и почвой большое. Сколько оборотов сделает колесо к тому моменту, когда стержень сделает один оборот?Задача по физике - 442
Педали трехколесного велосипеда соединены с задним колесом с помощью цепи. В какую сторону поедет велосипед, если, привязав к нижней педали веревку, потянуть за нее вперед? В какую сторону поедет велосипед, если на него сядет мальчик и носком ботинка будет толкать нижнюю педаль вперед? Объяснить почему.
Задача по физике - 443
Мяч брошен вертикально вверх. Что больше: время подъема или время падения?
Задача по физике - 449
Оцените, на какую высоту поднимется стрела, пущенная из лука вертикально вверх. Масса стрелы $m = 20 г$, длина тетивы $l = 1м$. Тетиву оттягивают на $h_ <0>= 5 см$. Силу упругости натяжения тетивы считать постоянной и равной 250 Н.
Задача по физике - 454
На гладком горизонтальном столе лежат два одинаковых кубика массой $m$ каждый. Кубики соединены пружинкой жесткости $k$. Длина пружинки в нерастянутом состоянии $l_<0>$ (рис.). На левый кубик внезапно начинает действовать сила $\bar$, постоянная по модулю и направлению. Найдите минимальное и максимальное расстояние между кубиками при движении системы.Задача по физике - 458
На гладком столе расположена система грузов, изображенная на рисунке. Коэффициент трения между грузами $M$ и $m$ равен $\mu$. Правый (по рисунку) нижний груз тянут вдоль стола с силой $\barЗадача по физике - 459
Конькобежец на ледяной дорожке старается пройти вираж как можно ближе к внутренней бровке. Велосипедист же на велотреке проходит вираж возможно дальше от внутренней бровки. Как объяснить это различие в движении конькобежца и велосипедиста на вираже? Профиль трека изображен на рисунке.Задача по физике - 460
Оценить максимальную силу, которую будет показывать динамометр, присоединенный между плоскостями, закрывающими магдебургские полушария полусферы с радиусом $R = 20 см$ (рис.). Полусферы растягиваются в противоположные стороны. Атмосферное давление равно $10^ <5>Па$.Задача по физике - 461
В стакан с водой, вращающийся вокруг своей оси, бросают шарик, который плавает на поверхности воды (рис.) В каком месте поверхности будет находиться шарик?Задача по физике - 466
В камеру сгорания реактивного двигателя (рис.) поступает в секунду масса $m$ водорода и необходимое для полного сгорания количество кислорода. Площадь сечения выходного отверстия сопла двигателя $S$, давление в этом сечении $p$, абсолютная температура $T$. Определить силу тяги двигателя.Задача по физике - 470
Шестиугольный карандаш толкнули вдоль горизонтальной плоскости, как показано на рисунке. При каких значениях коэффициента трения $\mu$ между карандашом и плоскостью карандаш будет скользить по плоскости не вращаясь?Задача по физике - 471
Кубик из пенопласта массой $M = 100 г$ лежит на горизонтальной подставке (рис.). Высота кубика $h = 10 см$. Снизу кубик пробивает вертикально летящая пуля массой $m = 10 г$. Скорость пули при входе в кубик $v_ <1>= 100 м/с$, при вылете $v_ = 95 м/с$. Подпрыгнет ли кубик?Задача по физике - 473
К динамометру приложена сила 4 Н так, что он движется с постоянным ускорением по горизонтальному столу. Что показывает динамометр, если масса пружины равна массе корпуса?
Задача по физике - 474
На гладкий горизонтальный стол поставили вертикально гантельку, состоящую из невесомого стержня с двумя одинаковыми маленькими шариками на концах (рис.). Верхнему шарику ударом сообщают скорость $v$ в горизонтальном направлении. При какой минимальной длине гантельки $l$ нижний шарик сразу оторвется от стола?Задача по физике - 455
Фотографировать тигра с расстояния менее 20 м опасно. Какой размер может иметь камера-обскура с отверстием диаметром в 1 мм, чтобы тигр на фотографии был полосатым? Расстояние между полосами на шкуре тигра равно 20 см.
Задача по физике - 456
В герметически закрытом сосуде в воде плавает кусок льда массой $M = 0,1 кг$, в который вмерзла дробинка массой $m = 5 г$. Какое количество тепла нужно затратить, чтобы дробинка начала тонуть? Плотность свинца $11,3 г/см^<3>$, плотность льда $0,9 г/см^<3>$, теплота плавления льда $3,3 \cdot 10^ Дж/кг$. Температура воды в сосуде равна $0^C$.
Задача по физике - 457
К ящику с двумя клеммами подключили: амперметр, резистор сопротивлением $m = 4 Ом$ и источник постоянного напряжения $U_ <1>= 5 В$ (рис.). Амперметр показал силу тока $I_<1>= 1 А$. Когда вместо источника напряжения $U_<1>$ включили другой источник напряжения $U_ = 20 В$, амперметр показал силу тока $I_ = 2А$. Что находится внутри ящика?Задача по физике - 462
Свет от источника $S$ двумя путями приходит к экрану, проходя через стеклянные прямоугольные призмы А и В (рис.). Длина каждой из призм $l$. Скорость света в воздухе равна $c$. Показатель преломления стекла $n$. Насколько быстрее свет пройдет по нижнему пути, если призму В привести в движение в сторону экрана со скоростью $v$?Задача по физике - 463
Три тела с массами $m_<1>, m_, m_$ могут скользить вдоль горизонтальной прямой без трения (рис.), причем $m_ <1>\gg \m_$ и $m_ \gg \m_$. Определить максимальные скорости двух крайних тел, если в начальный момент они покоились, а среднее тело имело скорость $\bar$. Удары считать абсолютно упругими.Задача по физике - 464
Шар радиуса $R$ соскальзывает по лестнице, ширина и высота ступенек которой $a \ll R$ (рис.). Соударения шара со ступеньками неупругие, трения нет. Какой наибольшей скорости достигнет шар при достаточно большой длине лестницы?Задача по физике - 465
В цилиндре с поршнем находится вода, внутри которой в начальный момент имеется полость объема $V$ (рис.). Давление паров в полости пренебрежимо мало. Поршень оказывает на воду постоянное давление $р$. Какую кинетическую энергию приобретает вода в момент, когда полость исчезнет? Начальная скорость частичек воды равна нулю. Силу тяжести не учитывать.Задача по физике - 467
На рисунке показана часть схемы, состоящей из резисторов, сопротивления которых неизвестны. Как, имея амперметр, вольтметр, источник тока и соединительные провода, можно определить сопротивление одного из резисторов, не разрывая ни одного контакта в схеме?Задача по физике - 468
К маятнику АВ с шариком массой $M$ подвешен маятник ВС с шариком массой $m$ (рис.). Точка А совершает колебания в горизонтальном направлении с периодом $T$. Найти длину нити ВС, если известно, что нить АВ все время остается вертикальной.
Динамика: движения системы связанных тел.
Проецирование сил нескольких объектов.
Действие второго закона Ньютона на тела, которые скреплены нитью
Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.
А для тех, кто все помнит, поехали!
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?
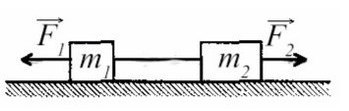
Движение происходит только на оси X.
Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.
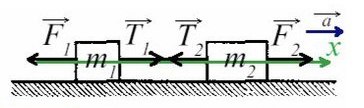
По II з. Ньютона спроецируем силы обоих тел на Ох:
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T ₁ и Т ₂.
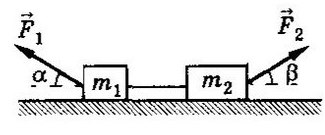
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.
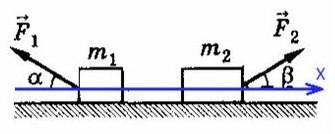
По II з. Ньютона спроецируем силы обоих тел на Ох:
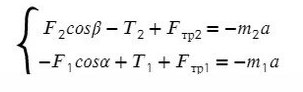
Сложим уравнения и выразим ускорение:
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:
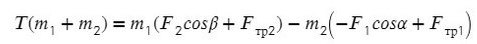
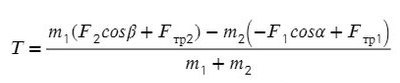
Задача 3 . Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?
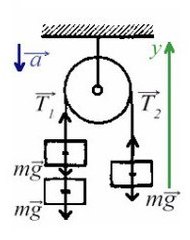
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.
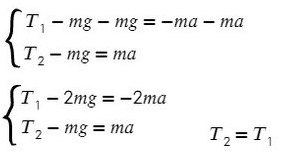
Вычтем из первого уравнения второе:
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.
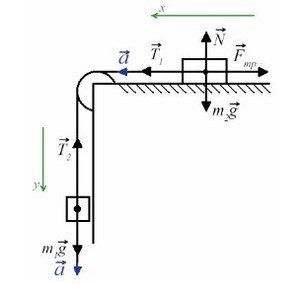
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):
(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)
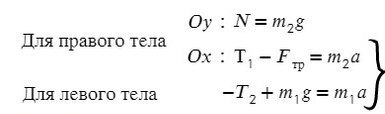
Сложим два нижних уравнения для того, чтобы T сократилось:
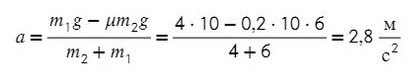
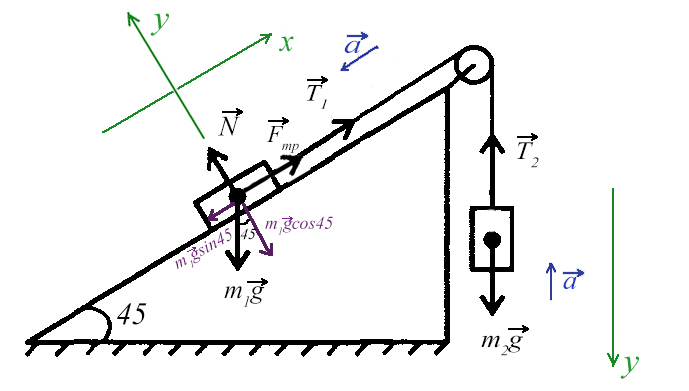
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?
Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.
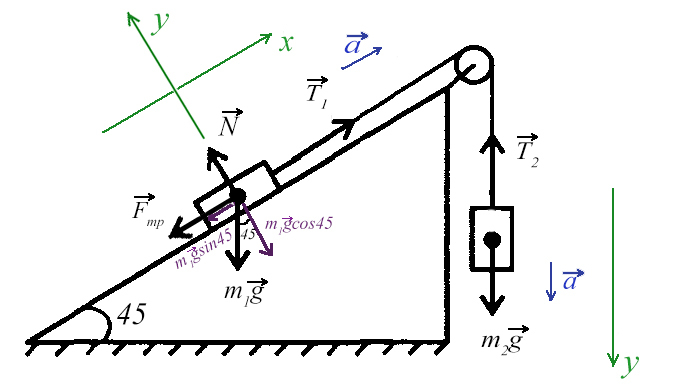
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):
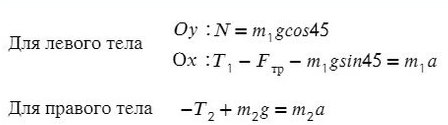
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:
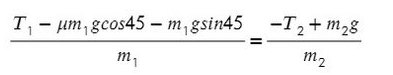
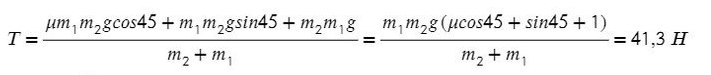
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:
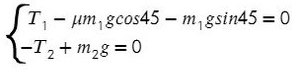
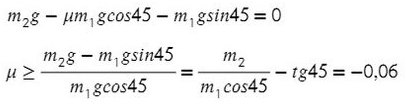
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.
Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.
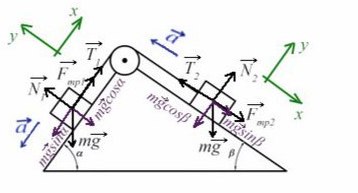
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:
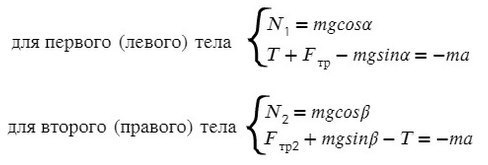
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:
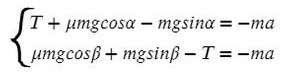
Сложим уравнения и сократим на массу:
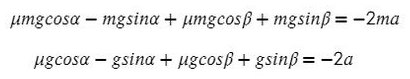
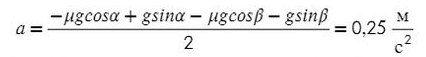
Подставив в любое уравнение найденное ускорение, найдем Т:
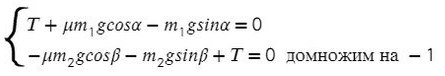
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:
Получили, что отношение масс должно быть таким:
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.
У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.
В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.
Читайте также:
