К телу массой 3 кг лежащему на столе привязали нить другой конец
Динамика:
Динамика материальной точки
§ 26. Определение сил по заданному движению
Задачи с решениями
26.1 В шахте опускается равноускоренно лифт массы 280 кг. В первые 10 с он проходит 35 м. Найти натяжение каната, на котором висит лифт.
РЕШЕНИЕ
26.2 Горизонтальная платформа, на которой лежит груз массы 1,02 кг, опускается вертикально вниз с ускорением 4 м/с2. Найти силу давления, производимого грузом на платформу во время их совместного спуска.
РЕШЕНИЕ
26.3 К телу массы 3 кг, лежащему на столе, привязали нить, другой конец которой прикреплен к точке A. Какое ускорение надо сообщить точке A, поднимая тело вверх по вертикали, чтобы нить оборвалась, если она рвется при натяжении T=42 Н.
РЕШЕНИЕ
26.4 При подъеме клетки лифта график скоростей имеет вид, изображенный на рисунке. Масса клетки 480 кг. Определить натяжения T1, T2, T3 каната, к которому привешена клетка, в течение трех промежутков времени: 1) от t = 0 до t = 2 c; 2) от t = 2 до t = 8 с и 3) от t = 8 с до t = 10 c.
РЕШЕНИЕ
26.5 Камень массы 0,3 кг, привязанный к нити длины 1 м, описывает окружность в вертикальной плоскости. Определить наименьшую угловую скорость ω камня, при которой произойдет разрыв нити, если сопротивление ее разрыву равно 9 Н.
РЕШЕНИЕ
26.6 На криволинейных участках железнодорожного пути возвышают наружный рельс над внутренним для того, чтобы сила давления проходящего поезда на рельсы была направлена перпендикулярно полотну дороги. Определить величину h возвышения наружного рельса над внутренним при следующих данных: радиус закругления 400 м, скорость поезда 10 м/с, расстояние между рельсами 1,6 м.
РЕШЕНИЕ
26.7 В вагоне поезда, идущего сначала по прямолинейному пути, а затем по закругленному со скоростью 20 м/с, производится взвешивание некоторого груза на пружинных весах; весы в первом случае показывают 50 Н, а на закруглении 51 Н. Определить радиус закругления пути.
РЕШЕНИЕ
26.8 Гиря массы 0,2 кг подвешена к концу нити длины 1 м; вследствие толчка гиря получила горизонтальную скорость 5 м/с. Найти натяжение нити непосредственно после толчка.
РЕШЕНИЕ
26.9 Груз М массы 0,102 кг, подвешенный на нити длины 30 см в неподвижной точке O, представляет собой конический маятник, т. е. описывает окружность в горизонтальной плоскости, причем нить составляет с вертикалью угол 60°. Определить скорость v груза и натяжение T нити.
РЕШЕНИЕ
26.10 Автомобиль массы 1000 кг движется по выпуклому мосту со скоростью v=10 м/с. Радиус кривизны в середине моста ρ=50 м. Определить силу давления автомобиля на мост в момент прохождения его через середину моста.
РЕШЕНИЕ
26.11 В поднимающейся кабине подъемной машины производится взвешивание тела на пружинных весах. При равномерном движении кабины показание пружинных весов равно 50 Н, при ускоренном — 51 Н. Найти ускорение кабины.
РЕШЕНИЕ
26.12 Масса кузова трамвайного вагона 10000 кг. Масса тележки с колесами 1000 кг. Определить силу наибольшего и наименьшего давления вагона на рельсы горизонтального прямолинейного участка пути, если на ходу кузов совершает на рессорах вертикальные гармонические колебания по закону x=0,02 sin 10t м.
РЕШЕНИЕ
26.13 Поршень двигателя внутреннего сгорания совершает горизонтальные колебания согласно закону x = r(cos ωt + (r cos 2ωt)/(4l)) см, где r — длина кривошипа, l — длина шатуна, ω — постоянная по величине угловая скорость вала. Определить наибольшее значение силы, действующей на поршень, если масса последнего M.
РЕШЕНИЕ
26.14 Решето рудообогатительного грохота совершает вертикальные гармонические колебания с амплитудой a=5 см. Найти наименьшую частоту k колебаний решета, при которой куски руды, лежащие на нем, будут отделяться от него и подбрасываться вверх.
РЕШЕНИЕ
26.15 Тело массы 2,04 кг совершает колебательное движение по горизонтальной прямой согласно закону x=10 sin(πt/2) м. Найти зависимость силы, действующей на тело, от координаты x, а также наибольшую величину этой силы.
РЕШЕНИЕ
26.16 Движение материальной точки массы 0,2 кг выражается уравнениями x=3 cos 2πt см, y=4 sin πt см (t в с). Определить проекции силы, действующей на точку, в зависимости от ее координат.
РЕШЕНИЕ
26.17 Шарик, масса которого равна 100 г, падает под действием силы тяжести и при этом испытывает сопротивление воздуха. Движение шарика выражается уравнением x = 4,9t – 2,45(1 - e-2t), где x — в метрах, t — в секундах, ось Ох направлена по вертикали вниз. Определить силу сопротивления воздуха R и выразить ее как функцию скорости шарика.
РЕШЕНИЕ
26.18 Масса стола строгального станка 700 кг, масса обрабатываемой детали 300 кг, скорость хода стола v=0,5 м/с, время разгона t=0,5 c. Определить силу, необходимую для разгона (считая движение равноускоренным) и для дальнейшего равномерного движения стола, если коэффициент трения при разгоне f1=0,14, а при равномерном движении f2=0,07.
РЕШЕНИЕ
26.19 Груженая вагонетка массы 700 кг опускается по канатной железной дороге с уклоном α=15°, имея скорость v=1,6 м/с. Определить натяжение каната при равномерном спуске и при торможении вагонетки. Время торможения t=4 c, общий коэффициент сопротивления движению f=0,015. При торможении вагонетка движется равнозамедленно.
РЕШЕНИЕ
26.20 Груз массы 1000 кг перемещается вместе с тележкой вдоль горизонтальной фермы мостового крана со скоростью v=1 м/с. Расстояние центра тяжести груза до точки подвеса l=5 м. При внезапной остановке тележки груз по инерции будет продолжать движение и начнет качаться около точки подвеса. Определить наибольшее натяжение каната при качании груза.
РЕШЕНИЕ
26.21 Определить отклонение α от вертикали и силу давления N вагона на рельс подвесной дороги при движении вагона по закруглению радиуса R=30 м со скоростью v=10 м/с. Масса вагона 1500 кг.
РЕШЕНИЕ
26.22 Масса поезда без локомотива равна 2*105 кг. Двигаясь по горизонтальному пути равноускоренно, поезд через 60 с после начала движения приобрел скорость 15 м/с. Сила трения равна 0,005 веса поезда. Определить натяжение стяжки между поездом и локомотивом в период разгона.
РЕШЕНИЕ
26.23 Спортивный самолет массы 2000 кг летит горизонтально с ускорением 5 м/с2, имея в данный момент скорость 200 м/с. Сопротивление воздуха пропорционально квадрату скорости и при скорости в 1 м/с равно 0,5 Н. Считая силу сопротивления направленной в сторону, обратную скорости, определить силу тяги винта, если она составляет угол в 10° с направлением полета. Определить также величину подъемной силы в данный момент.
РЕШЕНИЕ
26.24 Грузовой автомобиль массы 6000 кг въезжает на паром со скоростью 6 м/с. Заторможенный с момента въезда на паром автомобиль остановился, пройдя 10 м. Считая движение автомобиля равнозамедленным, найти натяжение каждого из двух канатов, которыми паром привязан к берегу. При решении задачи пренебречь массой и ускорением парома.
РЕШЕНИЕ
26.25 Грузы A и B веса PA=20 Н и PB=40 Н соединены между собой пружиной, как показано на рисунке. Груз А совершает свободные колебания по вертикальной прямой с амплитудой 1 см и периодом 0,25 c. Вычислить силу наибольшего и наименьшего давления грузов А и В на опорную поверхность CD.
РЕШЕНИЕ
26.26 Груз массы M=600 кг посредством ворота поднимают по наклонному шурфу, составляющему угол 60° с горизонтом. Коэффициент трения груза о поверхность шурфа равен 0,2. Ворот радиуса 0,2 м вращается по закону φ=0,4t3. Найти натяжение троса, как функцию времени и значение этого натяжения через 2 с после начала подъема.
РЕШЕНИЕ
26.27 Самолет, пикируя отвесно, достиг скорости 300 м/с, после чего летчик стал выводить самолет из пике, описывая дугу окружности радиуса R=600 м в вертикальной плоскости. Масса летчика 80 кг. Какая наибольшая сила прижимает летчика к креслу?
РЕШЕНИЕ
26.28 Груз M веса 10 Н подвешен к тросу длины l=2 м и совершает вместе с тросом колебания согласно уравнению φ = π/6 sin 2πt, где φ — угол отклонения троса от вертикали в радианах, t — время в секундах. Определить натяжения T1 и T2 троса в верхнем и нижнем положениях груза.
РЕШЕНИЕ
26.29 Велосипедист описывает кривую радиуса 10 м со скоростью 5 м/сек. Найти угол наклона срединной плоскости велосипеда к вертикали, а также тот наименьший коэффициент трения между шинами велосипеда и полотном дороги, при котором будет обеспечена устойчивость велосипеда.
РЕШЕНИЕ
26.30 Велосипедный трек на кривых участках пути имеет виражи, профиль которых в поперечном сечении представляет собой прямую, наклонную к горизонту, так что на кривых участках внешний край трека выше внутреннего. С какой наименьшей и с какой наибольшей скоростью можно ехать по виражу, имеющему радиус R и угол наклона к горизонту α, если коэффициент трения резиновых шин о грунт трека равен f?
РЕШЕНИЕ
26.31 Во избежание несчастных случаев, происходивших от разрыва маховиков, устраивается следующее приспособление. В ободе маховика помещается тело A, удерживаемое внутри его пружиной S; когда скорость маховика достигает предельной величины, тело А концом своим задевает выступ В задвижки CD, которая и закрывает доступ пара в машину. Пусть масса тела А равна 1,5 кг, расстояние e выступа В от маховика равно 2,5 см, предельная угловая скорость маховика 120 об/мин. Определить необходимый коэффициент жесткости пружины c (т. е. величину силы, под действием которой пружина сжимается на 1 см), предполагая, что масса тела А сосредоточена в точке, расстояние которой от оси вращения маховика в изображенном на рисунке положении равно 147,5 см.
РЕШЕНИЕ
26.32 В регуляторе имеются гири A массы 30 кг, которые могут скользить вдоль горизонтальной прямой MN; эти гири соединены пружинами с точками M и N; центры тяжести гирь совпадают с концами пружин. Расстояние конца каждой пружины от оси O, перпендикулярной плоскости рисунка, в ненапряженном состоянии равно 5 см, изменение длины пружины на 1 см вызывается силой в 200 Н. Определить расстояние центров тяжести гирь от оси O, когда регулятор, равномерно вращаясь вокруг оси O, делает 120 об/мин.
РЕШЕНИЕ
26.33 Предохранительный выключатель паровых турбин состоит из пальца A массы m=0,225 кг, помещенного в отверстии, просверленном в передней части вала турбины перпендикулярно оси, и отжимаемого внутрь пружиной; центр тяжести пальца отстоит от оси вращения вала на расстоянии l=8,5 мм при нормальной скорости вращения турбины n=1500 об/мин. При увеличении числа оборотов на 10% палец преодолевает реакцию пружины, отходит от своего нормального положения на расстояние x=4,5 мм, задевает конец рычага B и освобождает собачку C, связанную системой рычагов с пружиной, закрывающей клапан парораспределительного механизма турбины. Определить жесткость пружины, удерживающей тело A, т.е. силу, необходимую для сжатия ее на 1 см, считая реакцию пружины пропорциональной ее сжатию.
РЕШЕНИЕ
26.34 Точка массы m движется по эллипсу x2/a2+y2/b2=1. Ускорение точки параллельно оси y. При t=0 координаты точки были x=0, y=b, начальная скорость v0. Определить силу, действующую на движущуюся точку в каждой точке ее траектории.
РЕШЕНИЕ
26.35 Шарик массы m закреплен на конце вертикального упругого стержня, зажатого нижним концом в неподвижной стойке. При небольших отклонениях стержня от его вертикального равновесного положения можно приближенно считать, что центр шарика движется в горизонтальной плоскости Oxy, проходящей через верхнее равновесное положение центра шарика. Определить закон изменения силы, с которой упругий, изогнутый стержень действует на шарик, если выведенный из своего положения равновесия, принятого за начало координат, шарик движется согласно уравнениям x=a cos kt, y=b sin kt, где a, b, k — постоянные величины.
РЕШЕНИЕ
К телу массой 3 кг лежащему на столе привязали нить другой конец
Учебники для 3 семестра / Теор.мех / doc1
Ускорение точки может быть также определено, если задано время t движения, путь s, пройденный точкой, или конечная скорость при равнопеременном движении.
При прямолинейном движении
то ускорение при условии, что начальная скорость v 0 = 0, можно определить по формулам
В большинстве задач движение точки является несвободным, поэтому при их решении необходимо в соответствии с принципом освобождаемое™ от связей отбросить наложенную на точку связь, заменив ее реакцией связи, и рассматривать точку как свободную.
Тогда второй закон динамики примет вид
— сумма активных сил, действующих на точку; N — реак-
Записав это уравнение в проекциях на оси декартовых координат или на естественные оси, можно найти неизвестную силу N.
26. Определение сил по заданному движению
Последовательность решения задач этого параграфа:
1. Определить объект движения, т.е. движение какого тела или точки следует рассматривать.
3. Показать на рисунке объект движения в промежуточном положении в выбранной системе отсчета и все силы, действующие на него, включая и реакцию связи.
4. Записать второй закон динамики в векторной форме и в проекциях на выбранные оси или одну из осей.
5. Определить ускорение движения тела (точки), если оно не задано, в соответствии с приведенными выше указаниями.
6. Найти искомые величины в общем виде, а затем подставить числовые значения.
Задачи и решения
В шахте опускается равноускоренно лифт массы 280 кг. В первые 10 с он проходит 35 м. Найти натяжение каната, на котором висит лифт.
Так как лифт совершает прямолинейное движение, то направим ось х в сторону движения (начало отсчета точка О). Изобразим лифт в промежуточном положении и покажем на рисунке действующие на него силы: mg — сила тяжести, N — натяжение каната. Запишем уравнение движения в проекции на ось х:
Из формулы (1) определим
Так как лифт движется прямолинейно и равноускоренно, то можно записать
IX. Динамика материальной точки
Подставим в формулу (2) выражение Jc и найдем натяжение каната
О т в е т : 2548 Н.
Горизонтальная платформа, на которой лежит груз массы I 02 кг опускается вертикально вниз с ускорением 4 м/с 2 . Найти силу давления, производимого грузом на платформу во время Их совместного спуска.
На рис. 1 показано движение платформы с телом, на рис 2 - движущееся тело и действующие на него силы: mg - сила тяжести ~ Р е ^ЦИя опоры. Причем реакция Я опоры численно равна давлению N груза на платформу, но противоположна по направлению т.е. R — N . Для груза, принимаемого за материальную точку, в про-
екции на ось х можно записать
R = m(g-a) = 1, 02(9,80 -
О т в е т : 5,92 Н.
К телу массы 3 кг, лежащему на столе, привязали нить, другой конец которой прикреплен к точке А. Какое ускорение надо сообщить точке А, поднимая тело вверх по вертикали, чтобы нить оборвалась, если она рвется при натяжении Т = 42 Н?
Покажем на рисунке действующие на тело силы: mg —
сила тяжести, N — реакция нити. Запишем уравнение
движения тела в проекции на ось х:
Так как нить оборвется при N = Т, то из формулы (1)
О т в е т : 4,2 м/с 2 .
При подъеме клетки лифта график
скоростей имеет вид, изображенный на
рисунке. Масса клетки 480 кг. Опреде-
лить натяжения Т х , Т 2 , Т ъ каната, к ко-
торому привешена клетка, в течение
трех промежутков времени:
до / = 2 с; 2) от / = 2 до / = 8 с и 3) от / = 8
Покажем на рисунке силы, действующие на клеть лифта: mg — сила тяжести, Т— сила натяжения каната. Запишем уравнение движения клетки лифта в проекции на ось х:
ma = Т-mg =>Т = m(g + а).
По графику скоростей найдем:
Т х = 480(9,8 + 2,5) = 5904 (Н);
Т г =480-93 =4704 (Н);
Камень массы 0,3 кг, привязанный к нити длины 1 м, описывает окружность в вертикальной плоскости. Определить наименьшую угловую скорость to камня, при которой произойдет разрыв нити, если сопротивление ее разрыву равно 9 Н.
Так как натяжение нити, на которой подвешен камень, будет максимальным в нижнем положении, то покажем на рисунке силы, действующие на камень в этом положении: силу тяжести mg, силу натяжения Т нити. Запишем второй закон динамики в векторной форме:
и в проекции на ось и:
Приняв значение Т, равное заданному допускаемому сопротивлению разрыва нити, найдем минимальную угловую скорость to вращения нити, при которой произойдет ее разрыв:
О т в е т : co min = 4,494 рад/с.
На криволинейных участках железнодорожного пути возвышают наружный рельс над внутренним для того, чтобы сила давления проходящего поезда на рельсы была направлена перпендикулярно полотну дороги. Определить величину А возвышения наружного рельса над внутренним при следующих данных: радиус закругления 400 м, скорость поезда 10 м/с, расстояние между рельсами 1,6 м.
Будем считать, что радиус закругления относится к осевой линии пути. Выберем естественные оси (и, т, Ь) так, что соприкасающаяся плоскость хп — горизонтальна. Покажем на рисунке силы, действующие на поезд: mg — сила тяжести, N — нормальная реакция полотна дороги, равная по абсолютной величине давлению поезда на полотно
и направленная к нему перпендикулярно. Запишем дифференциальные уравнения движения в проекциях на выбранные оси:
Тогда проекции силы на оси х и п:
Модуль силы определяется по формуле
Лекции по физике (1 семестр) / Сем1_ст_Лекция 3
Гравитационная сила возникает между всеми телами, обладающими массой, всегда носит характер притяжения.
Для двух материальных точек (частиц) или однородных тел сферической формы гравитационную силу можно вычислить по закону всемирного тяготения:
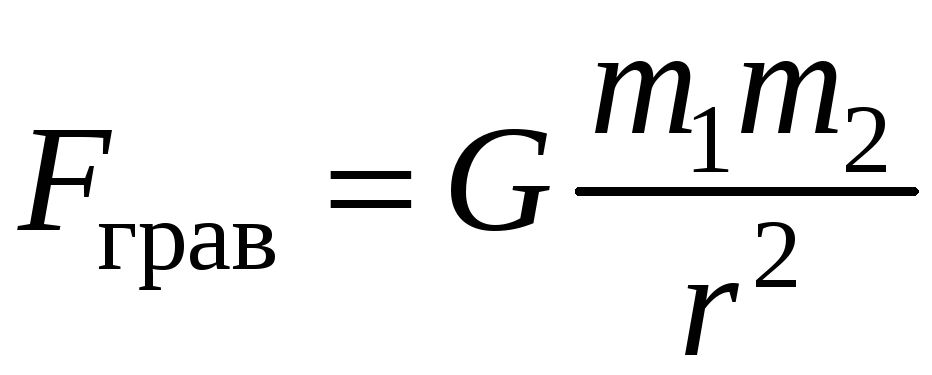
(3-1)
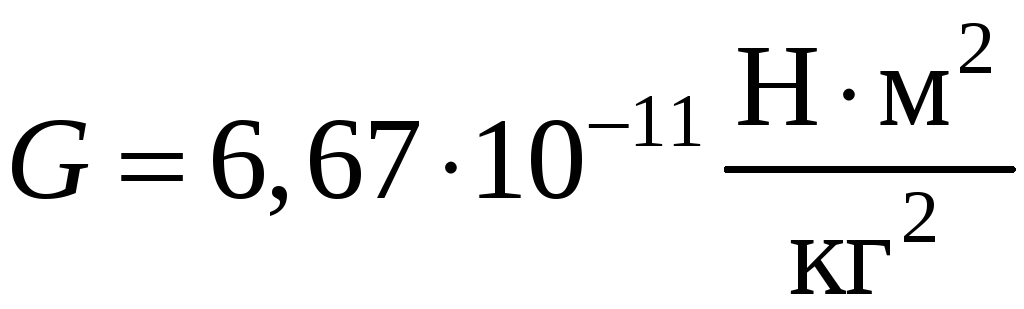
где гравитационная постоянная;
m гравитационная масса, кг;
r расстояние между частицами или центрами сферических тел.
Опыт Кавендиша
1798 г.
Если m1 = МЗ масса Земли, а m2 = m масса любой частицы, находящейся на расстоянии r = RЗ + h от центра Земли (RЗ радиус Земли), то гравитационную силу, с которой Земля притягивает к себе любую частицу, называют силой тяжести и вычисляют по формуле:
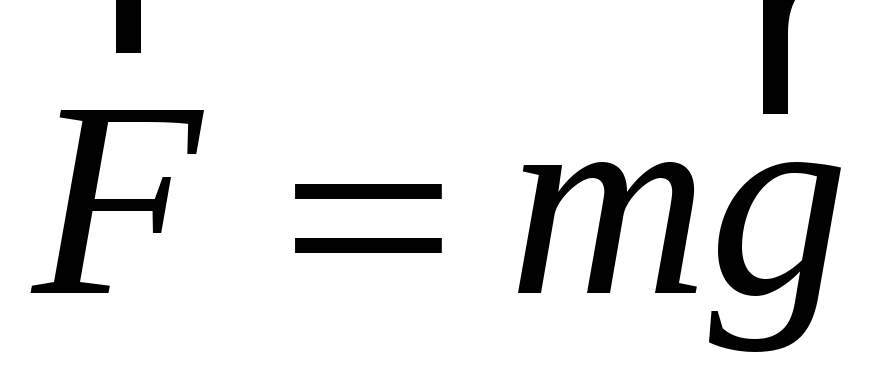
(3-2)
где ускорение свободного падения на высоте h над поверхностью Земли.
Вблизи поверхности Земли (h RЗ)

Сила тяжести в ИСО всегда направлена вниз, к центру Земли.
По третьему закону Ньютона
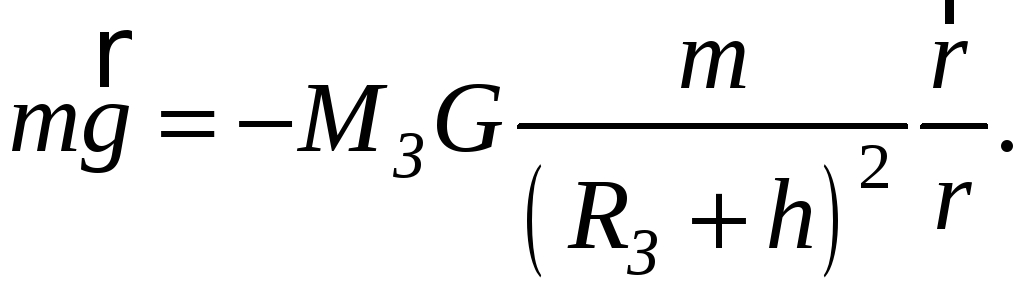
(сила тяжести, с которой Земля притягивает к себе любое тело, равна по величине и противоположна по направлению силе, с которой тело притягивает к себе Землю !).
Сила упругости возникает в упругих телах при их деформации (сжатии или растяжении), всегда направлена в сторону, противоположную деформации (рис.), и вычисляется по закону Гука:
Fх = – kx, (3-3)
где k – коэффициент упругости (жесткости) тела, Н/м.
Для металлического стержня:
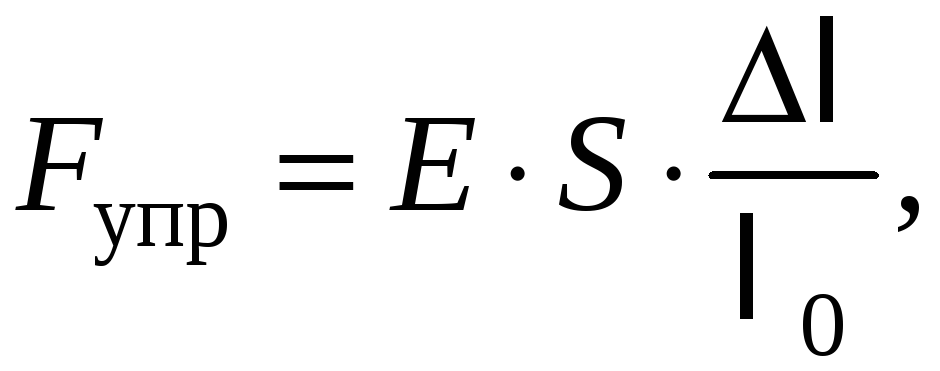
(3-4)

где модуль Юнга, Н/м 2 = Па;

площадь поперечного сечения стержня, м 2 ;

первоначальная длина стержня, м;
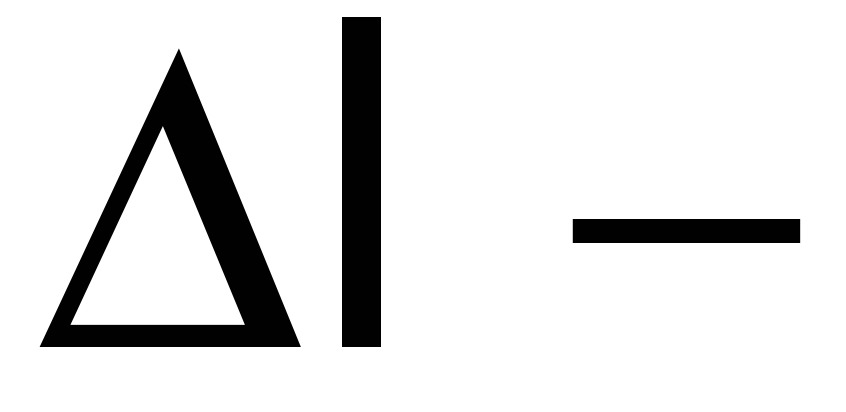
деформация стержня, м.
Если на опору или подвес действует сила, то в них возникает сила упругости, которую называют силой реакции опоры или силой натяжения . Сила всегда перпендикулярна опоре и направлена от нее (см. рис. а, б), а сила – вдоль подвеса (рис. в, г).
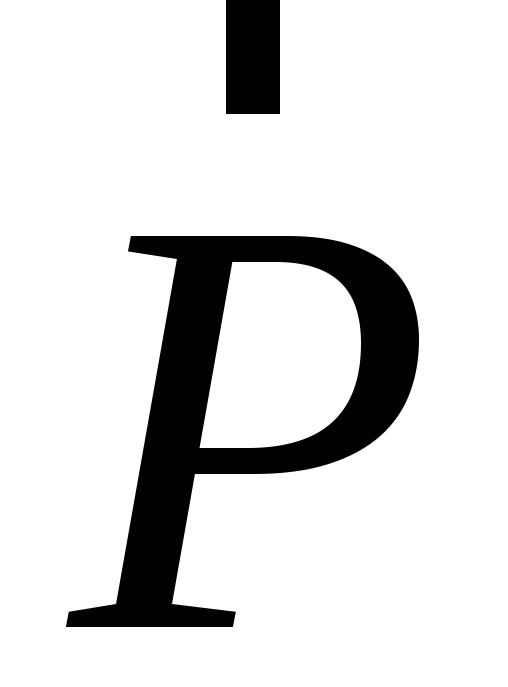
Вес тела – сила, с которой тело действует на опору или растягивает подвес из-за гравитационного притяжения.
или (3-5)

поэтому для вычисления веса тела необходимо вычислить силу N или и приравнять их к весу.

Вес тела может быть больше силы тяжести (P > mg) (перегрузка), меньше силы тяжести (P < mg) и равен нулю (невесомость).
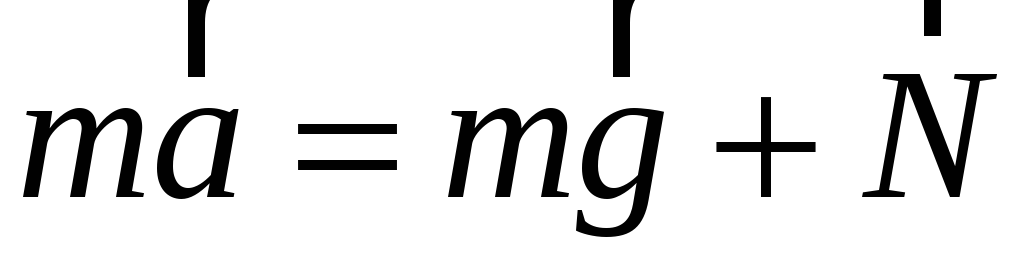
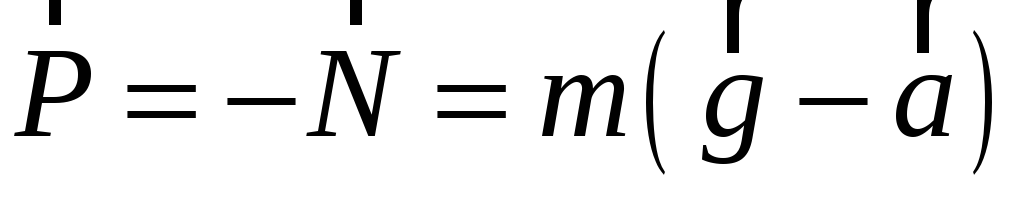

перегрузка

невесомость
Трение: внешнее (сухое) и внутреннее (жидкостное, вязкое).
Внешнее трение: покоя, скольжения и качения.
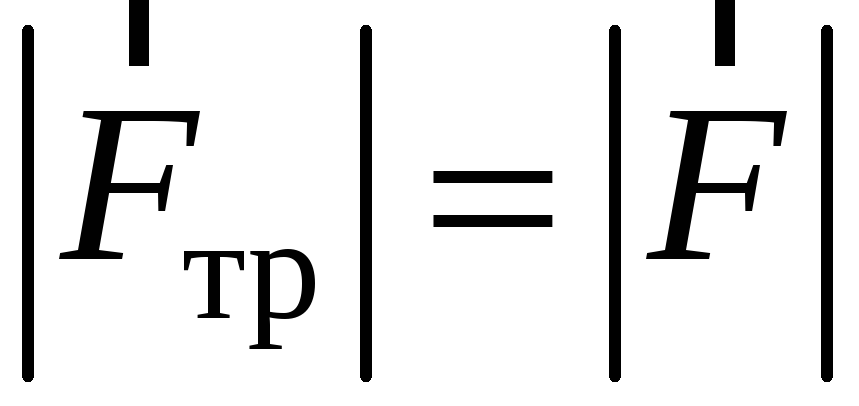
Для автомобилей, локомотивов и других тел роль силы тяги выполняет сила трения покоя.
Сила трения скольжения возникает при скольжении одного тела по поверхности другого, всегда направлена в сторону, противоположную относительному движению.
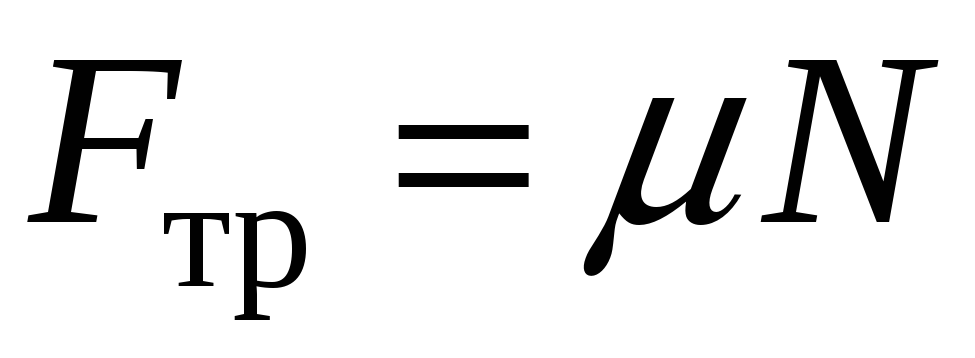
(3-6)
г коэффициент трения скольжения.

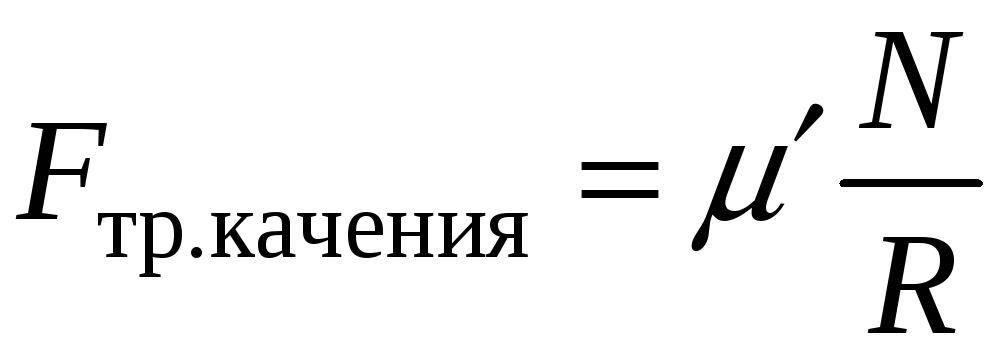
(3-6а)
где R радиус катящегося колеса;
' коэффициент трения качения.
Внутреннее (вязкое) трение возникает при движении тела в жидкости или газе.

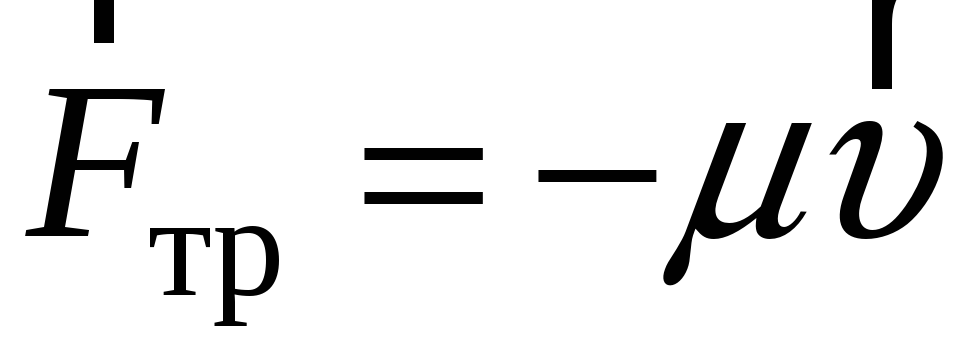
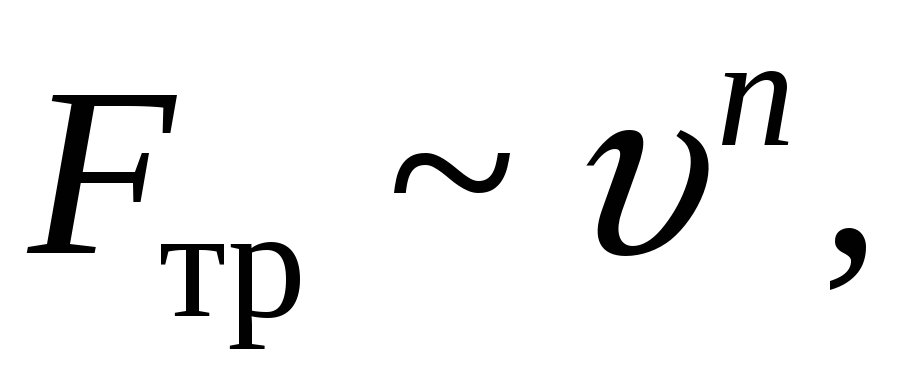
Турбулентный режим n = 2, 3, …
Выталкивающая сила Архимеда возникает при погружении тела в жидкость или газ, всегда направлена вверх против силы тяжести и вычисляется по закону Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной жидкости или газа.
(3-7)
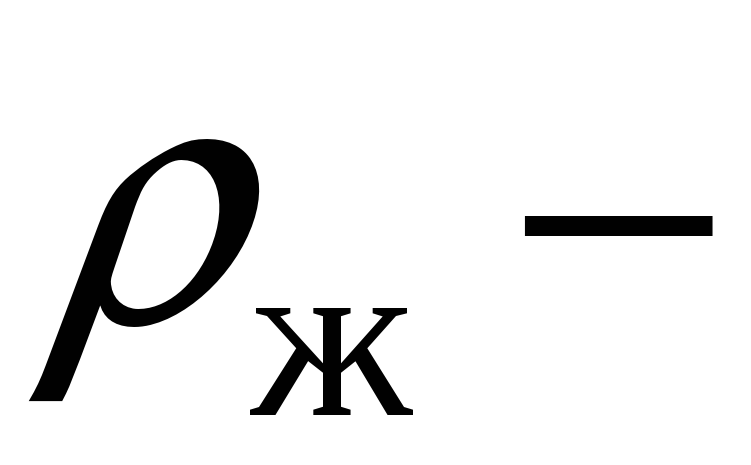
плотность жидкости
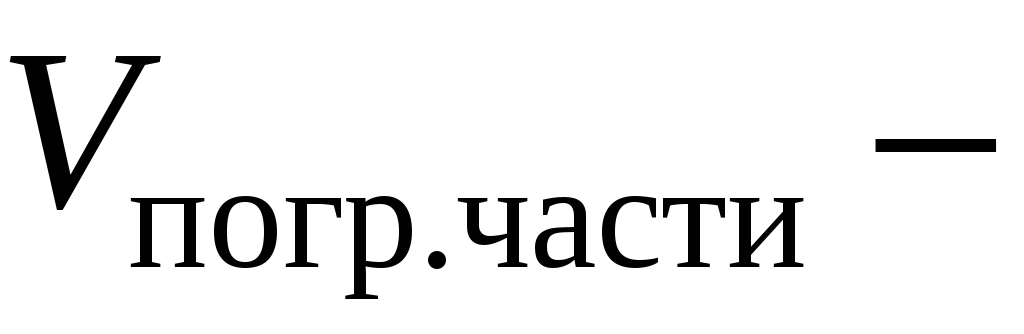
объем погруженной части тела
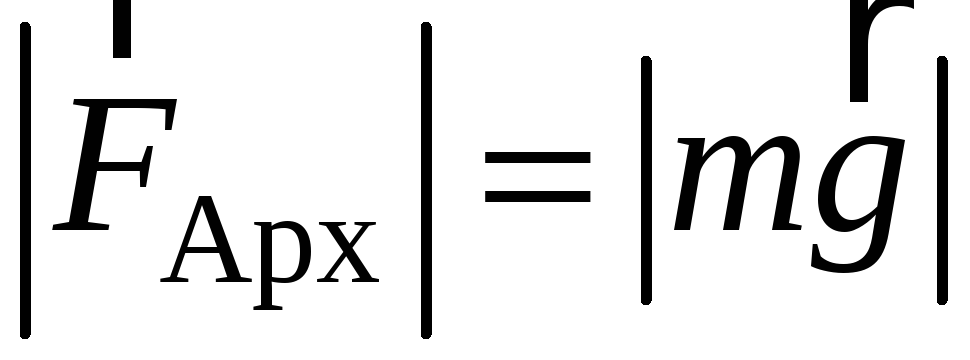
Условие плавания тела:
Если на частицу действует несколько сил, то руководствуются принципом независимости сил (каждая сила действует независимо от других) и принципом суперпозиции сил (результирующая сила (равнодействующая) определяется векторной суммой отдельных сил, действующих на частицу:

(3-8)
Тогда основное уравнение динамики материальной точки (частицы):
в ИСО произведение массы частицы на ее ускорение равно векторной сумме всех сил, действующих на эту частицу:
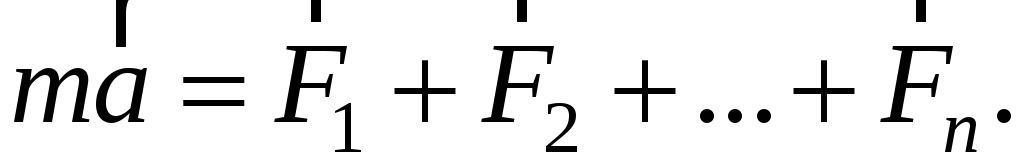
(3-9)
Для записи этого векторного уравнения в скалярной форме выбирают удобную ИСО (ось ОХ направляют по направлению движения, вдоль скорости) и находят проекции всех векторов на координатные оси:
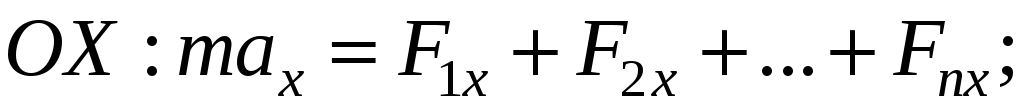

Проекции вектора на координатные оси вычисляются по формулам:
Fx = F cos;
Fy = F cos = F cos(90 ) = Fsin,

где , углы между направлением вектора и направлением соответствующей координатной оси.
Пример. К бруску массой 2 кг, лежащему на столе, привязана невесомая нерастяжимая нить, перекинутая через невесомый неподвижный блок, закрепленный на краю стола. Ко второму концу нити прикреплена гиря массой 1 кг. Найти модуль ускорения бруска, если коэффициент трения бруска о поверхность стола равен 0,02.
Читайте также:
