Брусок массой м скользит по горизонтальной поверхности стола и нагоняет брусок массой 4м
С2-1. На космическом аппарате, находящемся вдали от Земли, начал работать реактивный двигатель. Из сопла ракеты ежесекундно выбрасывается 2 кг газа (Δ m/Δt = 2 кг/с) со скоростью v = 500 м/с. Исходная масса аппарата М = 500 кг. Какую скорость приобретет аппарат, пройдя расстояние S = 36 м? Начальную скорость аппарата принять равной нулю. Изменением массы аппарата за время движения пренебречь.
С2-3. На гладкой горизонтальной плоскости покоится длинная доска массой М = 2 кг. На доске лежит шайба массой m = 0,5 кг. В начальный момент времени шайбе щелчком сообщили скорость v0 = 2 м/с. Коэффициент трения между шайбой и доской μ = 0,2. Сколько времени потребуется для того, чтобы шайба перестала скользить по доске?
А22-1.Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в неподвижно висящий на нити груз массой 81 г, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова длина нити?
А22-2.Летящая горизонтально пластилиновая пуля массой 9 г попадает в неподвижно висящий на нити длиной 40 см груз массой 81 г, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом α = 60°. Какова скорость пули перед попаданием в груз?
А22-3.Перед ударом два пластилиновых шарика движутся взаимно перпендикулярно с одинаковыми импульсами 1 кг•м/с. Массы шариков 100 г и 150 г. После столкновения слипшиеся шарики движутся поступательно. Их общая кинетическая энергия после соударения равна
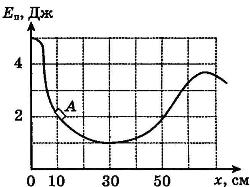
С1-1. После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме. В некоторый момент времени льдинка находилась в точке А с координатой х = 10 см и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
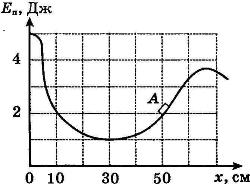
С1-2. После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от ее координаты в яме. В некоторый момент времени льдинка находилась в точке А с координатой х = 50 см и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
С2-3. Пуля летит горизонтально со скоростью v0 = 150 м/с, пробивает стоящий на горизонтальной поверхности льда брусок и продолжает движение в прежнем направлении со скоростью V0/3. Масса бруска в 10 раз больше массы пули. Коэффициент трения скольжения между бруском и льдом μ = 0,1. На какое расстояние S сместится брусок к моменту, когда его скорость уменьшится на 10%?
С2-4.Пуля летит горизонтально со скоростью v0 = 160 м/с, пробивает стоящую на горизонтальной шероховатой поверхности коробку и продолжает движение в прежнем направлении со скоростью V0/4. Масса коробки в 12 раз больше массы пули. Коэффициент трения скольжения между коробкой и поверхностью μ= 0,3. На какое расстояние S переместится коробка к моменту, когда её скорость уменьшится на 20%?
С2-5. Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m 2 = 300 г. В результате абсолютно неупругого соударения общая кинетическая энергия брусков становится равной 2,5 Дж. Определите высоту наклонной плоскости h. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
С2-6. Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с высоты h = 0,8 м и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m 2 = 300 г. Считая столкновение абсолютно неупругим, определите общую кинетическую энергию брусков после столкновения. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
С2.7. Брусок массой m1 = 500 г соскальзывает по наклонной плоскости высотой h = 0,8 м и сталкивается с неподвижным бруском массой m2 = 300 г, лежащим на горизонтальной поверхности. Считая столкновение упругим, определите кинетическую энергию первого бруска после столкновения. Трением при движении пренебречь.
С2.8. Брусок массой m 1 = 600 г, движущийся со скоростью v1 = 2 м/с, сталкивается с неподвижным бруском массой m 2 = 200 г. Какой будет скорость первого бруска после столкновения? Удар считать центральным и абсолютно упругим.
С2.9. Брусок массой m скользит по горизонтальной поверхности стола и нагоняет брусок массой 6m, скользящий по столу в том же направлении. В результате неупругого соударения бруски слипаются. Их скорости перед ударом были v0 = 7 м/с и v0/3. Коэффициент трения скольжения между брусками и столом μ = 0,5. На какое расстояние переместятся слипшиеся бруски к моменту, когда их скорость станет 2v0/7?
С2-10. Шайба массой m начиняет движение по желобу АВ из точки А из состояния покоя. Точка А расположена выше точки Н на высоте H = 6 м. В процессе движения по желобу механическая энергия шайбы из-за трения уменьшается на ΔE = 3 Дж. В точке В шайба вылетает из желоба под углом α = 15 0 к горизонту и падает на землю в точке D, находящейся на одной горизонтали с точкой В (см, рисунок). Найдите массу шайбы m . Сопротивлением воздуха пренебречь.
С2-11. Шайба массой m = 100 г начинает движение по желобу АВ из точки А из состояния покоя. Точка А расположена выше точки В на высоте Н = 6 м. В процессе движения по желобу механическая энергия шайбы из-за трения уменьшается на ΔE = 2 Дж. В точке В шайба вылетает из желоба поз углом α = 15 0 к горизонту и падает на землю в точке D. находящейся на одной горизонтали с точкой В (см. рисунок). Найдите BD. Сопротивлением воздуха пренебречь.
С2-12. Небольшая шайба после удара скользит вверх по наклонной плоскости из точки А (см. рисунок). В точке В наклонная плоскость без излома переходит в наружную поверхность горизонтальной трубы радиусом R. Если в точке А скорость шайбы превосходит v0 = 4 м/с, то в точке В шайба отрывается от опоры. Длина наклонной плоскости АВ = L = 1 м, угол α = 30°. Коэффициент трения между наклонной плоскостью и шайбой μ = 0,2. Найдите внешний радиус трубы R.
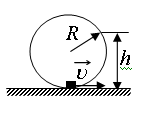
С2.13. Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закреплённого кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?
Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закреплённой сферы. Груз m находится в точке А на вершине сферы (см. рисунок). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу М, если m = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.
С2.15.Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закреплённого кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?
С2-16. Кусок пластилина сталкивается с покоящимся на горизонтальной поверхности стола бруском и прилипает к нему. Скорость пластилина перед ударом равна vпл = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ = 0,25. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 40%?
С2.17. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно и равны vпл = 15 м/с и vбр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ = 0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?
С2-18. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены взаимно противоположно и равны v пл =15 м/с и vбр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ = 0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится в 2 раза?
С2-19. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены взаимно противоположно и равны v пл = 15 м/с и v бр = 5 м/с. Масса бруска в 4 раза больше массы пластилина. К моменту, когда скорость слипшихся бруска и пластилина уменьшилась в 2 раза, они переместились на 0,22 м. Определите коэффициент трения μ бруска о поверхность стола.
С2-20. Пуля летит горизонтально со скоростью v0 = 150 м/с, пробивает стоящий на горизонтальной поверхности льда брусок и продолжает движение в прежнем направлении со скоростью v0/3. Масса бруска в 10 раз больше массы пули. Коэффициент трения скольжения между бруском и льдом μ = 0,1. На какое расстояние S сместится брусок к моменту, когда его скорость уменьшится на 10%?
С2.21. Пуля, летящая горизонтально со скоростью vo = 120 м/с, пробивает лежащую на горизонтальной поверхности стола коробку и продолжает движение в прежнем направлении, потеряв 80% скорости. Масса коробки в 16 раз больше массы пули. Коэффициент трения скольжения между коробкой и столом μ = 0,5. На какое расстояние переместится коробка к моменту, когда её скорость уменьшится вдвое?
С2-22. От удара копра массой 450 кг, падающего свободно с высоты 5 м, свая массой 150 кг погружается в грунт на 10 см. Определите силу сопротивления грунта, считая ее постоянной, а удар — абсолютно неупругим. Изменением потенциальной энергии сваи в поле тяготения Земли пренебречь.
С2.23. Пушка, закрепленная на высоте 5 м, стреляет в горизонтальном направлении снарядами массы 10 кг. Вследствие отдачи ее ствол, имеющий массу 1000 кг, сжимает на 1 м пружину жесткости 6•10 3 Н/м, производящую перезарядку пушки. Считая, что относительная доля η = 1/6 энергии отдачи идет на сжатие пружины, найдите дальность полета снаряда.
С2.24. Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
С2.25. Каково среднее давление пороховых газов в стволе орудия, если скорость вылетевшего из него снаряда равна 1,5 км/с? Длина ствола 3 м, его диаметр 45 мм, масса снаряда 2 кг. (Трение пренебрежимо мало.)
С2-26. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок). На краю трамплина скорость гонщика направлена под таким углом к горизонту, что дальность его полёта максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова высота полёта h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
С2-27. При выполнении трюка «Летающий велосипедист» гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 30° к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящийся на той же высоте, что и край трамплина. Какова дальность полета L на этом трамплине? Сопротивлением воздуха и трением пренебречь.
С2-28. При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты Н (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземлился на горизонтальный стол на той же высоте, что и край трамплина. Каково время полета?
С2-29. Шарик скользит без трения по наклонному желобу, а затем движется по «мертвой петле» радиуса R. С какой силой давит шарик на желоб в верхней точке петли, если масса шарика 100 г, а высота, с которой его отпускают, равна 4 R считая от нижней точки петли?
С2-30. Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна 500 м/с. В точке максимального подъема снаряд разорвался на два осколка. Первый упал на землю вблизи точки выстрела, имея скорость в 2 раза больше начальной скорости снаряда, а второй в этом же месте — через 100 с после разрыва. Чему равно отношение массы первого осколка к массе второго осколка? Сопротивлением воздуха пренебречь.
Брусок массой м скользит по горизонтальной поверхности стола и нагоняет брусок массой 4м
2011 год 115 вариант С2
Небольшая шайба массой m = 10 г, начав движение из нижней точки закреплённого гладкого кольца радиусом R = 0,14 м, скользит по его внутренней поверхности. На высоте h = 0,18 м она отрывается от кольца и свободно падает. Какую кинетическую энергию имела шайба в начале движения? (Решение)
2011 год 201 вариант С2
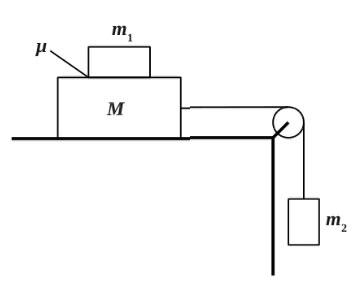
Система грузов Μ, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола горизонтальная гладкая. Коэффициент трения между грузами Μ и m1 равен μ= 0,2 . Грузы Μ и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть Μ = 1,2 кг , m1 = m2 = m . При каких значениях m грузы Μ и m1 движутся как одно целое? (Решение)
2011 год. 01-2 вариант. С2
На горизонтальном столе лежит деревянный брусок. Коэффициент трения между поверхностью стола и бруском µ = 0,1. Если приложить к бруску силу, направленную вверх под углом α = 45° к горизонту, то брусок будет двигаться по столу равномерно. С каким ускорением будет двигаться этот брусок по столу, если приложить к нему такую же по модулю силу, направленную под углом β = 30° к горизонту? (Решение)
2011 год. 01-1 вариант. С2
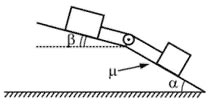
В изображенной на рисунке системе нижний брусок может даигаться по наклонной плоскости, составляющей с горизонтом угол α = 30°, а верхний брусок - вдоль наклонной плоскости, составляющей с горизонтом некоторый угол β. Коэффициент трения между нижним бруском и плоскостью равен μ = 0,2, трение между верхним бруском и наклонной плоскостью отсутствует. Считая соединяющую бруски нить очень легкой и нерастяжимой, и пренебрегая массой блока и трением в его оси найдите, при каких значениях угла β нить будет натянута. (Решение)
2011 год. 00 вариант. С1
Две одинаковые лодки двигались в озере параллельными курсами со скоростями v1 и v2 > v1. В тот момент, когда лодки поравнялись, из первой лодки во вторую переложили рюкзак. Как при этом изменилась (увеличилась, уменьшилась, осталась без изменений) скорость второй лодки? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения. (Трением пренебречь). (Решение)
2010 год. 301 вариант. С2
Шарик массой m = 200 г , подвешенный к потолку на легкой нерастяжимой нити длиной L = 1,5 м. Шарик привели в движение так, что он движется по окружности в горизонтальной плоскости, образуя конический маятник (см. рисунок). Модуль силы натяжения нити Т = 2,7 Н. Чему равен период обращения τ, за который маятник делает один оборот по окружности? (Решение)
2010 год. 151 вариант. С2
В безветренную погоду самолёт затрачивает на перелёт между городами 6 часов. Если во время полёта дует боковой ветер перпендикулярно линии полёта, то самолёт затрачивает на перелёт на 9 минут больше. Найдите скорость ветра, если скорость самолёта относительно воздуха постоянная и равна 328 км/ч. (Решение)
2010 год. 00 вариант. С2
На озере два рыбака сидят в покоящейся лодке, масса которой М = 100 кг и длина L= 6 м: один - на носу, а второй - на корме. Их массы равны соответственно m1 = 60 кг и m2= 80 кг. Насколько сместится лодка относительно берега озера, если второй рыбак перейдёт к первому? (Трением пренебречь.) (Решение)
2009 год 117 вариант А25
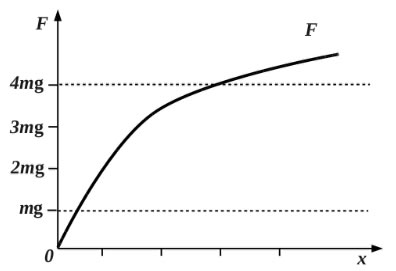
Период малых вертикальных колебаний груза массы m, подвешенного на резиновом жгуте, равен Т0. Зависимость силы упругости резинового жгута F от удлинения x изображена на графике. Период малых вертикальных колебаний груза массой 4m на этом жгуте - Τ удовлетворяет соотношению
1) Τ > 2 Т0; 2) Τ = 2 Т0; 3) Τ = Т0; 4) Τ < 0,5 Т0. (Решение)
2009 год. 135 вариант. С2
М = 2 кг. По доске скользит шайба массой m. Коэффициент трения между шайбой и доской μ = 0,2. В начальный момент времени скорость шайбы v0 = 2 м/с, а доска покоится. В момент t = 0,8 с шайба перестает скользить по доске. Чему равна масса шайбы m? (Решение)
2009 год. 107 вариант. С2
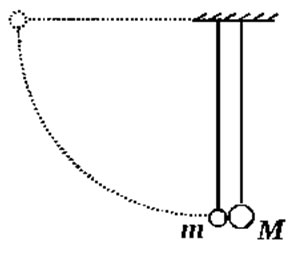
Два шарика, массы которых отличаются в 3 раза, висят соприкасаясь, на вертикальных нитях (см. рисунок). Лёгкий шарик отклоняют на угол 90° и отпускают без начальной скорости. Найти отношение импульса легкого шарика к импульсу тяжелого шарика сразу после абсолютно упругого центрального соударения. (Решение)
2009 год. 02 вариант. С2
Радиус планеты Плюк в 2 раза меньше радиуса Земли, а период обращения спутника, движущегося вокруг Плюка по низкой круговой орбите, совпадает с периодом обращения аналогичного спутника Земли. Чему равно отношение средних плотностей Плюка и Земли? Объём шара пропорционален кубу радиуса (V ~ R 3 ). (Решение)
2008 год. 01 вариант. С1
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м? (Решение)
2008 год. 46 вариант. С1
Тело, свободно падающее с некоторой высоты, за время t = 1 с после начала движения, проходит путь в n = 5 раз меньший, чем за такой же промежуток времени в конце движения. Найдите высоту, с которой падало тело. (Решение)
2008 год. 41 вариант. С1
Маленький шарик падает вертикально вниз на плоскость, имеющую угол наклона к горизонту 30° и упруго отражается от неё. Следующий удар шарика о плоскость происходит на расстоянии 20 см от места первого удара. Определите промежуток времени между первым и вторым ударами шарика о плоскость. (Решение)
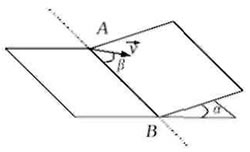
2007 год. 6 вариант. С1
Наклонная плоскость пересекается с горизонтальной плоскостью по прямой АВ. Угол между плоскостями α = 30°. Маленькая шайба начинает движение вверх по наклонной плоскости из точки А с начальной скоростью v под углом 60° к прямой АВ. В ходе движения шайба съезжает на прямую АВ в точке В. Найдите v, если АВ = 1 м. Трением между шайбой и наклонной плоскостью пренебречь. (Решение)
2007 год. 30 вариант. С1
Пушка, закрепленная на высоте 5 м, стреляет в горизонтальном направлении снарядами массы 10 кг. Вследствие отдачи ее ствол, имеющий массу 1000 кг, сжимает на 1 м пружину жесткости 6•10 3 Н/м, производящую перезарядку пушки. Считая, что относительная доля μ = 1/6 энергии отдачи идет на сжатие пружины, найдите дальность полета снаряда. (Решение)
2007 год. 25 вариант. C1
Брусок массой m скользит по горизонтальной поверхности стола и нагоняет брусок массой 6 m, скользящий по столу в том же направлении. В результате неупругого соударения бруски слипаются. Их скорости перед ударом были v0 = 7 м/с и v0/З. Коэффициент трения скольжения между брусками и столом μ = 0,5. На какое расстояние переместятся слипшиеся бруски к моменту, когда их скорость станет 2v0/7? (Решение)
2006 год. 61 вариант. С1
Мяч, брошенный под углом 45° к горизонту с расстояния L = 6,4 м от забора, перелетел через него, коснувшись его в самой верхней точке траектории. Какова высота забора над уровнем, с которого брошен мяч? (Решение)
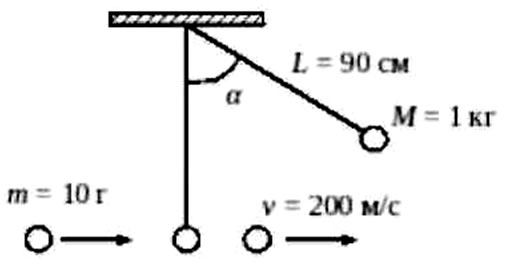
2006 год. 33 вариант. С1
Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60° и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару, она пробивает его и продолжает двигаться горизонтально со скоростью 200 м/с. С какой скоростью летела пуля, если шар, продолжая движение в горизонтальном направлении, отклоняется на угол 39°? (Массу шара считать неизменной, диаметр шара - пренебрежимо малым по сравнению с длиной нити, cos 39° = 7/9). (Решение)
2005 год. 91 вариант. С1
Пуля, летящая горизонтально со скоростью v0 = 120 м/с, пробивает лежащую на горизонтальной поверхности стола коробку и продолжает движение в прежнем направлении, потеряв 80% скорости. Масса коробки в 16 раз больше массы пули. Коэффициент трения скольжения между коробкой и столом μ = 0,5. На какое расстояние переместится коробка к моменту, когда её скорость уменьшится вдвое? (Решение)
2004 год. 99 вариант. С1
С некоторой высоты Н свободно падает стальной шарик. Через t = 1 с после начала падения он сталкивается с неподвижной плитой, плоскость которой наклонена под углом 45° к горизонту, и до момента падения на Землю пролетает по горизонтали расстояние S = 20 м. Каково значение Н? Сопротивление воздуха не учитывать. Удар шарика о плиту считать абсолютно упругим. (Решение)
2004 год. 119 вариант. C1
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости высотой h = 0,8 м и сталкивается с неподвижным бруском массой m2 = 300 г, лежащим на горизонтальной поверхности. Считая столкновение упругим, определите кинетическую энергию первого бруска после столкновения. Трением при движении пренебречь. (Решение)
2004 год. 97 вариант. С5
Брусок массой m1 = 1 кг лежит на наклонной плоскости с углом при основании, равным α = 53°. Коэффициент трения бруска с плоскостью равен μ = 0,5. К бруску привязана невесомая нить, другой конец которой перекинут через неподвижный идеальный блок. К этому концу нити подвешивается груз массой m2 = 1 кг. Определите, придет ли в движение брусок при подвешивании груза. Если придет в движение, то в каком направлении? (sin 53° = 0,8; cos 53° = 0,6) (Решение)
2002 год. 265 вариант. С1
Нить маятника длиной l = 1 м, к которой подвешен груз массы m = 0,1 кг, отклонена на угол α от вертикального положения и отпущена. Сила натяжения нити T в момент прохождения маятником положения равновесия равна 2 Н. Чему равен угол α? (Решение)
К железному бруску массой 7,8 кг привязали тонкую невесомую нерастяжимую нить, которую перекинули через неподвижный идеальный блок, а сам брусок целиком погрузили в воду (см. рис.). Свободный конец нити удерживают, действуя на него с некоторой силой так, что брусок находится в равновесии. Установите соответствие между физическими величинами и их численными значениями, выраженными в указанных единицах. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
А) модуль силы натяжения нити, Н
Б) объём бруска, дм 3
Зная массу железного бруска, можем найти его объем:
Запишем второй закон Ньютона для бруска:
Найдем отсюда модуль силы натяжения нити:
Тип 6 № 8899К алюминиевому бруску массой 5,4 кг привязали тонкую невесомую нерастяжимую нить, которую перекинули через неподвижный идеальный блок, а сам брусок целиком погрузили в воду (см. рис.). Свободный конец нити удерживают, действуя на него с некоторой силой так, что брусок находится в равновесии. Установите соответствие между физическими величинами и их численными значениями, выраженными в указанных единицах. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Зная массу алюминиевого бруска, можем найти его объем:
Аналоги к заданию № 8857: 8899 Все
Тип 30 № 29762По гладкой наклонной плоскости, составляющей угол с горизонтом, скользит из состояния покоя брусок массой В тот момент, когда брусок прошёл по наклонной плоскости расстояние в него попала и застряла в нём летящая навстречу ему вдоль наклонной плоскости пуля массой Скорость пули После попадания пули брусок поднялся вверх вдоль наклонной плоскости на расстояние от места удара. Найдите массу пули m. Трение бруска о плоскость не учитывать. Обоснуйте применимость используемых законов к решению задачи.
Обоснование.
Рассмотрим движение бруска и пули относительно Земли, которую можно считать инерциальной системой отсчета. Брусок и шарик движутся поступательно, поэтому их движение можно описывать моделью материальной точки. По условию поверхность наклонной плоскости гладкая, сила трения отсутствует. Сила реакции опоры перпендикулярна направлению движения, поэтому работу не совершает. В данном случае можно применять законы сохранения импульса и энергии.
Перейдем к решению.
1. Рассмотрим два состояния при движении бруска-в начальный момент времени и в момент попадания пули, который примем на нулевой уровень высоты. В первом состоянии брусок обладал потенциальной энергией причем по рисунку Во втором состоянии брусок обладал кинетической энергией По закону сохранения энергии
2. В результате неупругого взаимодействия бруска и пули они станут одним целым и будут двигаться со скоростью u в направлении движения пули. По закону сохранения импульса В проекции на ось Ox, направленную вверх вдоль наклонной плоскости, получаем
3. Рассмотрим два состояния бруска с пулей — в момент удара, который будем считать нулевым уровнем высоты, и в момент остановки при подъеме на некоторую высоту В первом состоянии тела обладают кинетической энергией во втором состоянии потенциальной энергией По закону сохранения энергии
4. Объединяя записанные уравнения, находим массу пули
Тип 30 № 25943На горизонтальном гладком столе лежит длинная доска массой M = 10 кг, а на её левом конце — деревянный брусок массой m = 1 кг (см. рис.). В брусок попадает и прилипает к нему пластилиновый снаряд массой m0 = 200 г, летевший горизонтально по направлению вдоль доски со скоростью V0 = 10 м/с, после чего брусок скользит до остановки по шероховатой доске, не сваливаясь с неё. Какое количество теплоты Q выделится в этой системе в течение всего процесса?
Какие законы Вы используете для описания взаимодействия бруска, доски и пули? Обоснуйте их применение к данному случаю.
Обоснование. Система «доска-брусок-пуля» является замкнутой, т. к. плоскость гладкая, сила трения не действует. Сила реакции опоры и сила тяжести направлены по вертикали, поэтому не оказывают влияния на горизонтальную скорость. В инерциальной системе отсчета применим закон сохранения импульса при абсолютно неупругом ударе.
При абсолютно неупругом ударе в инерциальной системе отсчета применим закон превращения энергии.
Перейдем к решению.
1. На всю систему «пуля + брусок + доска» по горизонтали не действуют внешние силы, поэтому справедлив закон сохранения проекции импульса по этому направлению: где V — скорость движения системы после остановки бруска. Таким образом,
2. В начальном состоянии механическая энергия системы равна кинетической энергии пули а в конечном — кинетической энергии системы
3. По закону изменения механической энергии разность этих кинетических энергий выделяется в виде теплоты:
Задания Д29 C2 № 10238 Задания Д29 C2 № 10302На горизонтальном гладком столе лежит длинная доска массой M = 5 кг, а на её левом конце — деревянный брусок массой m = 0,5 кг (см. рис.). В брусок попадает и прилипает к нему пластилиновый снаряд массой m0 = 230 г, летевший горизонтально по направлению вдоль доски со скоростью V0 = 200 м/с, после чего брусок скользит до остановки по шероховатой доске, не сваливаясь с неё. Какая часть начальной кинетической энергии «пули» перейдёт в этой системе в теплоту в течение всего процесса? Ответ выразите в процентах.
Аналоги к заданию № 10238: 10302 Все
Тип 30 № 25940Клин массой M с углом α при основании закреплён на шероховатой горизонтальной плоскости (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о верхнюю половину наклонной поверхности клина и о шероховатую горизонтальную плоскость равен Нижняя половина наклонной поверхности клина гладкая. Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.
Какие законы Вы используете для описания движения бруска по клину? Обоснуйте их применение к данному случаю.
Обоснование. Брусок движется поступательно, поэтому его можно считать материальной точкой. При движении бруска по шероховатой части клина и по шероховатой горизонтальной поверхности в инерциальной системе отсчета можно применить закон превращения энергии.
Перейдем к решению. При соскальзывании бруска с клина и дальнейшем его движении по горизонтальной плоскости до остановки выполняется закон изменения механической энергии данной системы тел: вся потенциальная энергия бруска расходуется на работу против сил трения скольжения при движении вначале по шероховатой части поверхности клина, Aтр1, а затем — по шероховатой горизонтальной плоскости, Aтр2:
mgH = Aтр1 + Aтр2.
По закону Амонтона — Кулона сила трения скольжения равна μN, где сила N давления бруска на неподвижную наклонную плоскость равна а на горизонтальную плоскость — mg. Силы трения на участках с трением равны соответственно и μmg. Вдоль участка наклонной плоскости с трением брусок прошёл расстояние, как следует из рисунка, так что Обозначим расстояние, которое брусок прошёл по горизонтальной плоскости, через l2. Тогда Aтр2 = μmgl2. Подставим выражения для работ против сил трения в закон изменения энергии: Отсюда получаем, что При соскальзывании с клина брусок сдвинулся по горизонтали на расстояние равное длине основания клина, так что искомое расстояние
Читайте также:
