Вертикально стоящий стальной стержень ведет себя странно
Поиск по сайту
Каталог задач
Механика
Кинематика
Механика жидкостей и газов
Молекулярная физика и термодинамика
Реальные газы
Насыщенные пары и жидкости
Твердые тела
Электричество
Постоянный ток
Магнетизм
Баллистической постоянной гальванометра называется величина, численно равная количеству электричества, которое вызывает отброс по шкале на одно деление.
α (в делениях шкалы)
Гармоническое колебательное движение и волны
Акустика
Электромагнитные колебания и волны
Геометрическая оптика и фотометрия
Построить график зависимости показателя преломления п материала пластинки от длины волны λ.
Волновая оптика
Элементы теории относительности
Тепловое излучение
Излучение считать абсолютно черным.
Квантовая природа света и волновые свойства частиц
Атом Бора. Рентгеновские лучи
Радиоактивность
Ядерные реакции
подвергаются превращению все ядра, находящиеся в массе т= 1 г алюминия? Какую энергию Q2 надо затратить, чтобы осуществить это превращение, если известно, что при бомбардировке ядра алюминия α-частицами с энергией W =8 МэВ только одна α-частица из n = 2·10 6 частиц вызывает превращение?
Какая масса тt водорода в единицу времени должна превращаться в гелий? Солнечная постоянная K = 1,37 кВт/м 2 . Принимая, что масса водорода составляет 35% массы Солнца, подсчитать, на какое время t хватит запаса водорода, если излучение Солнца считать постоянным.
Найти массу т нейтрона, если известно, что энергия γ-квантов W1 = 2,66 МэВ, а энергия вылетающих протонов, измеренная по производимой ими ионизации, оказалась равной W2 = 0,23 МэВ. Энергию нейтрона считать равной энергии протона. Массы дейтона и протона считать известными.
У к а з а н и е. Учесть, что при пороговом значении кинетической энергии бомбардирующей частицы относительная скорость частиц, возникающих в результате реакции, равна, нулю.
В Томском Политехническом Университете проходит уникальный эксперимент, который позволит изучить и улучшить свойство специальных алмазов, которые используются в Большой Адронном Коллайдере для фиксирования и регистрации элементарных частиц.
ЭКСПЕРИМЕНТ: БАК остро нуждается в детекторах для фиксирования элементарных частиц
Учёные из китайского университета электронных наук и технологий совместно с сотрудниками Хьюстонского университета из США провели многоэтапный эксперимент, в котором было показано, что лазерное излучение, действуя на мелкодисперсные наночастицы в жидкости (воде), порождает перепад гидродинамического давления, что приводит к движению потока жидкости.
ГИДРОДИНАМИКА: Эффект рождения гидродинамических потоков от ультразвуковых волн
Обычно пассивные электромагнитные компоненты двунаправленные, это обозначает одинаковое распространение сигналов противоположных друг другу. Циркулярные устройства обладают не равными модулями противоположных сигналов, что позволяет использовать их как хабы в топологии электрических цепей для различного распределения сигналов. До недавнего времени для работ с высокочастотными электромагнитными волнами применялись материалы исключительно из ферромагнетиков, что существенно повышало себестоимость и накладывает определённые неудобства для бытовой техники.
ЭЛЕКТРОНИКА: Создан безмагнитный кремниевый циркуляционный чип для диапазона миллиметровых волн
Физики из Национального института стандартов и технологий (США) добились одновременной квантовой запутанности сразу 219 ионов бериллия (9Be+). Эту систему ученые использовали для имитации магнитных материалов. Авторы отмечают, что максимальное количество ионов, которые удавалось запутать между собой в ранних экспериментах, не превышало 20 штук.
Исследования в физике элементарных частиц требуют больших энергозатрат и тем самым опосредованно влияют на климат. В недавней публикации впервые проводится сравнение пяти проектов будущей хиггсовской фабрики по энергопотреблению и по выбросам парниковых газов в расчете на один рожденный бозон Хиггса. В ближайшие годы стоит ожидать рост публикаций и мероприятий такой направленности.
Климатическая повестка проникает и в физику элементарных частиц
Идея, что в быстро летящем протоне может быть небольшая доля тяжелых «очарованных» кварков, была высказана почти полвека назад, но ее справедливость не удавалось подтвердить. Недавно коллаборация NNPDF, проанализировав огромный объем данных и обновив описание устройства протона, впервые получила указание на то, что очарованные кварки и антикварки действительно присутствуют в протоне.
Впервые получено указание на «внутреннее очарование» в протоне
Исторически концепция хиггсовского механизма восходит к исследованиям в области нерелятивистской физики конденсированных систем, выполненных в конце 1950-х и начале 1960-х годов одним из крупнейших специалистов в этой области Филипом Андерсоном. В день 10-летия с момента объявления об открытии бозона Хиггса вполне уместно подробно рассказать о жизни и работе Андерсона.
Филип Андерсон: добрый и злой гений бозона Хиггса
Десять лет назад на Большом адронном коллайдере был открыт бозон Хиггса — и с этого события можно отсчитывать начало новой эры исследований элементарных частиц. В этом обзоре мы кратко напомним, что за частица хиггсовский бозон, зачем физики его так пристально изучают, что про него уже известно к настоящему моменту и как будет развиваться физика хиггсовского бозона в будущем.
Вертикально стоящий стальной стержень ведет себя странно
Электродвигатель в реальном режиме развивает механическую мощность 2,5 кВт, работает 1 час и при этом потребляет электроэнергии 4,4 кВт-час. Какая доля потребленной электроэнергии затрачивается на механическую работу, то тесть каков КПД электродвигателя? Ответ округлить до целых.
Электродвигатель подъемного крана имеет КПД 40% и потребляет 100 кДж электроэнергии при равномерном подъеме груза. Выберите два верных утверждения.
При такой работе двигателя
1) он совершает 40 кДж работы
2) 60 кДж затрачивается на разгон вала электродвигателя
3) 60 кДж затрачивается на компенсацию работы сил трения груза о воздух
4) 60 кДж затрачивается на нагревание обмоток электродвигателя
5) 60 кДж затрачивается на согревание крановщика
Выберите два верных утверждения о принципах работы электродвигателя. В электродвигателе
1) используется воздействие магнитного поля на проводник с током
2) используется нагревание проводников при протекании по ним тока
3) механическая энергия деталей двигателя преобразуется в энергию движущихся зарядов
4) внутренняя энергия топлива преобразуется в механическую энергию деталей двигателя
5) энергия движущихся зарядов преобразуется в механическую энергию деталей двигателя
На двух закрепленных круглых проводниках, соединяемых с источником тока (см. рис.), лежат две проводящие перемычки круглого сечения. Что произойдет с перемычками при замыкании ключа? Установите соответствие между перемычками и описанием их поведения после замыкания ключа. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в ответ выбранную цифру под соответствующей буквой.

Заряженный ион влетает в однородное магнитное поле. На него действует сила. Укажите словом без пробелов (вверх, вниз, к наблюдателю, от наблюдателя) направление силы.

В магнитное поле влетают протон, электрон и нейтрон (см. рис.). Каким будет характер их дальнейшего движения? Установите соответствие между частицами и описанием их движения в магнитном поле.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в ответ выбранную цифру под соответствующей буквой.

На котором из рисунков правильно показано направление силы, действующей на проводник с током в магнитном поле постоянного магнита?

Квадратная рамка расположена в однородном магнитном поле в плоскости линий магнитной индукции (см. рис.). Направление тока в рамке показано стрелками. Как направлены силы, действующие на стороны аЪ и cd рамки со стороны внешнего магнитного поля В ? Поставьте в соответствие стороны рамки и направления сил, действующих на них. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в ответ выбранную цифру под соответствующей буквой.

Чему равна сила Ампера, действующая на провод длиной 10 см в магнитном поле с индукцией 0,04 Тл, когда по нему течет ток силой 8 А?

Чему равна сила Ампера, действующая на фрагмент проводника с током в однородном магнитном поле (см. рис.), если сила тока 5А, длина фрагмента 25 см, а индукция магнитного поля 0,02 Тл?

Куда направлена сила Ампера, действующая на проводник с током в однородном магнитном поле (см. рис.)? Запишите ответ словом без пробелов (вверх, вниз, вправо, влево, к наблюдателю, от наблюдателя).

Выберите два верных утверждения.
Увеличить массу стального груза, который удерживает электромагнит, можно
1) увеличив число витков обмотки электромагнита
2) уменьшив число витков обмотки электромагнита
3) изменив направление намотки провода на сердечник
4) увеличив длину сердечника
5) увеличив силу тока в обмотке электромагнита
Простейший электромагнит создается наматыванием провода в изолирую щ ей оболочке на стальной гвоздь и подключением его к полюсам пальчиковой батарейки. Выберите два верных утверждения о магнитны х полях двух изготовленных таким образом электромагнитов.
1) Магнитное поле намагниченного гвоздя гораздо сильнее магнитного поля намотанной в виде катушки проволоки
2) Магнитное поле намагниченного гвоздя гораздо слабее магнитного поля намотанной в виде катушки проволоки
3) У обоих электромагнитов северный полюс у шляпки гвоздя.
4) У левого электромагнита северный полюс у острия, у правого — у шляпки.
5) У правого электромагнита северный полюс у острия, у левого — у шляпки

Ток в кольце направлен по часовой стрелке. Куда направлено магнитное поле, созданное током в точке А , расположенной в плоскости кольца. Запишите цифру правильного ответа:
1) вверх,
2) вниз,
3) вправо,
4) влево,
5) к наблюдателю,
6) от наблюдателя.

На рисунке показана картина линий индукции магнитного поля, создаваемого прямым проводом с током. В какой из обозначенных точек магнитное поле максимально воздействует на магнитную стрелку или маленькую ненамагниченную иглу из стали?

Выберите два верных утверждения. Магнитное поле в пространстве создает
1) неподвижный заряженный шар
2) кольцо с током
3) Земля
4) лежащая на столе пластиковая линейка, потертая о шерсть
5) вода в стакане, постоявшем около сильного постоянного магнита
На рисунке показан фрагмент картины магнитного поля, изображенный с помощью линий индукции магнитного поля. В какой из указанных точек воздействие магнитного поля на маленькую стальную скрепку будет минимально?

Запишите словом, как направлен (вправо, влево, вверх, вниз) в точке А вектор индукции магнитного поля, фрагмент которого изображен на рисунке с помощью линий магнитной индукции.

Выберите два верных утверждения. Линии магнитного поля — это
1) линии, совпадающие с формой магнита
2) линии, по которым летит положительный заряд, попадая в магнитное поле
3) линии, по которым летит отрицательный заряд, попадая в магнитное поле
4) воображаемые линии, в каждой точке которых индукция магнитного поля направлена по касательной
5) линии, задающие направление в пространстве, вдоль которого ориентируется магнитная стрелка компаса
Поставьте в соответствие физические величины и математические модели, используемые для их описания. Каждому элементу первого столбца подберите утверждение из второго столбца и впишите в таблицу под заданием цифры, обозначающие номера выбранных утверждений.

Вертикально стоящий стальной стержень ведет себя «странно»: если обносить компас вокруг верхнего конца, стрелка компаса поворачивается к нему северным концом, если вокруг нижнего конца — южверным. Выберите описания двух экспериментов, которые могут подтвердить гипотезу о том, что явление объясняется намагничиванием стержня в магнитном поле Земли.
1) Прислонить поочередно к верхнему и нижнему концу стержня стальной ключ и посмотреть, притягивается ли он к нему.
2) Прислонить поочередно к верхнему и нижнему концу стержня медную скрепку и посмотреть, притягивается ли она к нему.
3) Поднести поочередно к верхнему и нижнему концу стержня бусинку, заряженную касанием эбонитовой палочки, и посмотреть, притягивается ли она к ним.
4) Поднести компас к середине стержня и посмотреть, ориентируется ли стрелка компаса.
5) Размагнитить стержень, нагревая его или подвергая вибрации, поставить вертикально и убедиться, что через некоторое время поведение стрелки компаса у верхнего и нижнего конца стержня опять стало «странным».
На рисунке изображена установка по изучению магнитного действия тока. Два одинаковых медных стержня укреплены над столом, а под ними располагается магнитная стрелка.
Опыт 1. При присоединении кольца 1 к клемме « + » аккумулятора и кольца 2 к клемме « —» магнитная стрелка повернулась на 45° к стержню.
Опыт 2. При присоединении колец 1 и 3 к клемме «+», а колец 2, 4 к клемме «-» стрелка повернулась на 90° северным концом от аккумулятора.
Опыт 3. При присоединении колец 1, 4 к клемме «4*», а колец 2, 3 к клемме «-» стрелка сохранила положение вдоль стержней.
Выберите два верных утверждения, являющихся выводами, сделанными на основании трех проведенных экспериментов.
1) Вектор индукции магнитного поля Земли направлен вдоль стержней от стойки Б к стойке А.
2) Вектор индукции магнитного поля Земли перпендикулярен стержням.
3) При протекании тока в направлении от стойки А к стойке Б вектор магнитной индукции поля, создаваемого током в стержне, направлен под стержнем справа налево.
4) В опыте 3 сила тока в стержнях была мала.
5) При протекании тока по стержням в противоположных направлениях магнитные поля двух токов компенсируют друг друга.

В опыте Эрстеда магнитная стрелка, направленная вдоль медного провода, поворачивается перпендикулярно ему при пропускании по проводу электрического тока. Выберите два верных утверждения. Магнитное поле Земли в лаборатории Эрстеда направлено
1) вдоль провода
2) перпендикулярно проводу
3) под углом 45° к проводу
4) в неизвестном направлении, поскольку о нем нельзя судить из опыта Эрстеда
5) в направлении северного конца магнитной стрелки до включения тока через провод
Рядом с прямым проводом расположена магнитная стрелка (см. рис.), показывающая направление магнитного поля Земли. Поставьте в соответствие описания экспериментов со сменой направления тока большой силы и описания поведения магнитной стрелки вблизи провода. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в ответ выбранную цифру под соответствующей буквой.

Выберите два верных утверждения. В опыте Эрстеда было обнаружено
1) отклонение магнитной стрелки от направления на север при протекании электрического тока по проводу
2) взаимодействие параллельных проводников с током
3) возникновение тока в замкнутой катушке при опускании в нее магнита
4) взаимодействие двух магнитных стрелок
5) поворот магнитной стрелки в положение, перпендикулярное проводу, при большой силе тока в этом проводе
На рисунке показано расположение двух стержневых магнитов. Какое из 4 направлений будет показывать северный полюс стрелки компаса, расположенного в точке А?

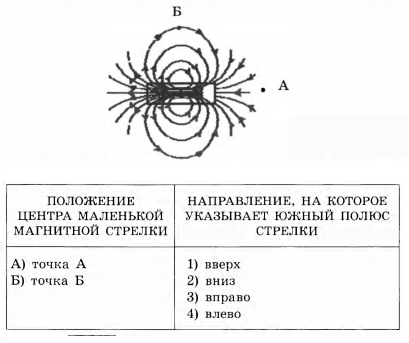
На рисунках показано расположение железных опилок на листе бумаги, под который подведены концы двух стержневых магнитов. Поставьте в соответствие рисунки и возможное расположение полюсов стержневых магнитов вблизи промежутка между ними. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в ответ выбранную цифру под соответствующей буквой.
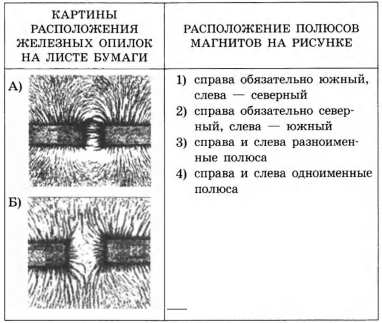
На рисунке показаны силовые линии стержневого магнита. Куда будет направлен южный полюс магнитной стрелки, если ее поместить в точки А и Б? Поставьте в соответствие положение центра маленькой магнитной стрелки и направление южного полюса магнитной стрелки. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в ответ выбранную цифру под соответствующей буквой.
На рисунке показано, как ориентируется магнитная стрелка компаса на поверхности стола, когда под крышкой стола параллельно ей расположен стержневой магнит так, что его центр лежит на середине отрезка АВ.
Вы берите два верных ответа. Это означает, что под столом магнит ориентирован так, что
1) под точкой А — северный полюс
2) под точкой В — северный полюс
3) под точкой А — южный полюс
4) под точкой В — южный полюс
5) под точкой С — северный полюс

На каком из рисунков правильно показаны силы взаим одействия двух магнитов, повернутых друг к другу противоположными полю сами?

Между полюсами подковообразного магнита помещают металлический гвоздь (см. рис.). Выберите два верных утверждения
1)Гвоздь из стали намагнититься,а из меди- нет
2)Гвоздь из стали намагнититься,а из стали- нет
3)Гвозди из стали и из меди намагнитятся.
4)У намагниченного гвоздя, вблизи шляпки окажется южный полюс.
5)У намагниченного гвоздя, вблизи шляпки окажется северный полюс.

Постоянный магнит подносят к двум скрепкам на одинаковое расстояние. Первая притягивается к магниту, вторая не притягивается. Выберите два верных утверждения.
Это могло произойти, если
1) первая скрепка сделана из стали, вторая из меди
2) первая скрепка сделана из меди, вторая из пластмассы
3) первая скрепка из стали, вторая из пластмассы
4) обе скрепки из стали, но первая скрепка была намагничена заранее, а вторая — нет
5) обе скрепки из меди, но первая скрепка была намагничена заранее, а вторая — нет
Выберите два верных утверждения. Если нос корабля в океане все время обращен по направлению конца N стрелки компаса, то он
1) приплывет на Северный географический полюс Земли
2) приплывет на Южный географический полюс Земли
3) приплывет на северный магнитный полюс Земли
4) приплывет на южный магнитный полюс Земли
5) проплывет примерно в 1500 км от Северного географического полюса Земли
Постоянный магнит подносят северным полюсом сначала к медной, затем к стальной скрепке. Выберите два верных утверждения, описывающих дальнейший процесс и его объяснение.
1) Ничего не происходит, так как скрепки не намагничиваются.
2) Стальная скрепка поворачивается к магниту.
3) Медная скрепка поворачивается к магниту.
4) У намагничивающейся скрепки на ближайшем к магниту конце образуется южный магнитный полюс.
5) У намагничивающейся скрепки на ближайшем к магниту конце образуется северный магнитный полюс.
Движение стержня
Наверняка все помнят ту вереницу однотипных и скучных задач по механике, которые приходилось решать в школе, а некоторым и в вузе. Подавляющее большинство таких задач действительно скучны — в них требуется взять стандартные заученные формулы, подставить друг в друга, иногда добавить числа и получить ни о чём не говорящий ответ. Такие задачи даются просто для закрепления материала, и в них, как правило, даже не требуется, чтобы решающий представлял себе явление.
Тем не менее даже в простой механике есть и другие задачи — задачи, в которых требуется прежде всего думать. Они не обязательно сложные, и для их решения часто можно обойтись горсткой школьных формул. Однако для того, чтобы догадаться, что именно писать и куда смотреть в поисках ответа, механическую систему из этой задачи надо хорошенько «прочувствовать». В таких задачах иногда встречаются небольшие ловушки или кажущиеся парадоксы, по крайней мере с точки зрения «обыденной» интуиции, натренированной на решении простых типовых задач. И наконец, при решении таких задач встречаются даже неожиданные приемы, отдаленно напоминающие методы настоящей теоретической физики. Предлагаемая ниже задача, как мне кажется, как раз из этой серии.
Рис. 1. Нижний конец стержня, опирающегося о гладкие стенку и пол, начинают тянуть с постоянной скоростью v. Какая скорость будет у точки A в момент удара об пол? (Рисунок автора задачи)
Задача
На концах тонкого, невесомого и абсолютно жесткого стержня длины L находятся две материальные точки массой m каждая. Первоначально стержень стоял, прислоненный к вертикальной стенке под некоторым углом, и опирался концом A на стенку и концом B на пол. Мы берем нижний конец стержня и тянем его вправо с небольшой, но постоянной скоростью v. Стержень начинает съезжать и через некоторое время падает на пол. Всё происходит в поле силы тяжести; трение стержня о стенку и пол отсутствует.
Вопрос: какова будет скорость точки A в момент удара об пол?
Подсказка 1
Кажется довольно естественным, что если скорость v мала, то стержень так и будет скользить, до самого конца опираясь на стенку. В этом случае связь между скоростями точек A и B находится без труда, и она приводит нас к следующем ответу: скорость точки A в момент удара об пол бесконечна.
Такой ответ, конечно, неудовлетворителен. Дело тут даже не в том, что «бесконечностей в природе не бывает» или «нельзя обогнать скорость света» — от этих возражений при желании можно отговориться. Проблема тут в том, что такой странный ответ возникает в ситуации, которая выглядит вполне реализуемой без каких-либо специальных ухищрений. Мы можем взять легкую палочку длиной 10 см и тянуть ее конец со скоростью 1 см/сек — но ответ нам говорит, что даже при таком скромном усилии мы сможем разогнать предмет до сколь угодно большой скорости! Очевидно (хотя бы на основании закона сохранения энергии), что тут что-то не так. Разнообразные уточнения про свойства палочки, про отсутствие трения и т. д. введены лишь для простоты расчетов и принципиальной картины не меняют.
Подсказка 2
Оплошность, про которую шла речь выше, заключается в предположении, что палочка всегда, до самого конца, будет опираться на стенку. На самом деле при некотором небольшом угле палочка начнет отъезжать от стенки, так что свободный конец будет падать свободно, не успевая долетать до стенки. Задача в результате разделяется на два отдельных этапа. Вначале надо доказать, что действительно будет момент отрыва, и найти, при каком угле наклона это произойдет, а уж затем решить отдельно задачу о движущейся и падающей палочке, но уже без стенки.
Для начала давайте получим тот неправильный ответ, который приводит к бесконечности. Если палочка фиксированной длины касается и стенки, и пола, то расстояния x и y по теореме Пифагора связаны соотношением: x 2 + y 2 = L 2 . Пусть в какой-нибудь момент угол наклона составляет α. Тогда y/x = tg α.
Рис. 2. Для вычисления связи между скоростями vA и vB полезно перейти в систему отсчета точки B. (Рисунок автора задачи)
Скорости скольжения vA и vB = v тоже связаны друг с другом из-за нерастяжимости палочки. Для того чтобы найти эту связь, можно перейти в систему отсчета точки B (см. рис. 2). В этой системе отсчета точка B неподвижна, а палочка прокручивается, опираясь на отъезжающую стенку. Скорость точки A в этой системе отсчета обязана быть направлена так, чтобы палочка не растягивалась и не сжималась. Из несложной тригонометрии получаем соотношение: vA = v·ctg α. Если предположить, что касание со стенкой длится вплоть до самого падения (α = 0), то по этой формуле vA в этот момент стремится к бесконечности.
Как понять, в какой именно момент палочка перестанет касаться стенки? Для этого надо перейти от кинематики к динамике — то есть надо «почувствовать» все силы, действующие на обе точки A и B, пока стержень касается и стенки, и пола. Подробный баланс сил для обеих точек с учетом того, что они движутся строго вдоль своих стенок, предлагается написать самостоятельно. Вам надо убедиться в том, что отрыв от стенки произойдет именно в тот момент, когда сила напряжения стержня станет равна нулю — то есть когда стержень из «сдавленного» состояния перейдет в «растягиваемое». После этого останется найти тот угол, при котором это происходит, и дальше уже переходить к этапу номер два.
Решение
Будем действовать пошагово. Шаг 1 (связь между скоростями точек A и B при двойном касании) уже сделан выше.
Рис. 3. Силы, действующие на оба конца стержня, в случае, когда он касается и стенки, и пола. Красным показаны силы, вызванные сопротивлением материалов, синим — сила тяжести, зеленым — «наша» сила Four, которая должна удерживать точку B от ускорения. (Рисунок автора задачи)
Шаг 2. Запишем все силы, действующие на точки A и B по горизонтали и по вертикали при двойном касании:
точка A: х: –T·cos α + FA = 0, y: T·sin α – mg = maA,
точка B: х: T·cos α + Four = 0, y: –T·sin α – mg + FB = 0.
Здесь FA и FB — силы реакции опоры со стороны стенки и пола, которые строго перпендикулярны поверхности, T — сила напряжения стержня, которую мы считаем положительной, если стержень сжат, и отрицательной — если он растянут (поэтому мы и говорим «сила напряжения», а не «сила натяжения»). Напомним, что стержень абсолютно жесткий, поэтому действующие в нём силы — будь то сила сдавливания или сила растяжения — не меняют его длины, но влияют на баланс сил на его концах. Наконец, Four — это та «наша» сила, которую мы прикладываем к нижней точке, чтобы она двигалась без ускорения, а лишь с постоянной скоростью v. Эта сила неизвестна, и более того, она переменная: в каждый момент времени она подстраивается так, чтобы скомпенсировать другую силу, действующую на точку B по горизонтали.
Заметим, что если сила напряжения может быть как положительной, так и отрицательной, то сила реакции опоры может быть только положительна. Отрицательная сила реакции опоры FA означала бы, что стержень прилип к стенке, а мы тянем стержень на себя и пытаемся его отодрать. Такого в нашей задаче быть не может, поскольку по условию стержень просто прислонен к стене.
Глядя на эти формулы, легко понять, что происходит в момент, когда стержень перестает касаться стенки. До тех пор пока он на нее опирается, сила FA положительна, и значит, сила напряжения T тоже положительна. Эта же сила напряжения толкает точку B вперед, значит наша внешняя сила Four отрицательна, то есть направлена к стенке. Иными словами, для того чтобы конец стержня двигался с постоянной скоростью, мы должны не тянуть его, а подталкивать против движения, сопротивляясь скатывающей силе, передающейся по стержню.
Как только сила напряжения сменится на отрицательную, в точке касания со стенкой перестанет действовать сила реакции опоры: FA = 0. Тогда никакая больше сила не сможет скомпенсировать горизонтальную проекцию силы T, и точка A в результате начнет двигаться в направлении от стенки. Поэтому именно T = 0 (а следовательно, и Four = 0) и есть тот момент, когда произойдет отрыв.
Шаг 3. Теперь необходимо выяснить, при каком угле наклона это произойдет. Это можно сделать разными способами, но здесь я хочу продемонстрировать несколько необычный прием. Мы сейчас покажем, что наша задача с математической точки зрения полностью эквивалентна другой задаче, совсем непохожей на исходную. Эту задачу мы сможем решить без труда и тем самым получим ответ на интересующий нас вопрос.
Рис. 4. Задача о скольжении стержня о стенку математически эквивалентна задаче о движении материальной точки по полукруглому холму в ослабленном поле тяжести. (Рисунок автора задачи)
Давайте обратим внимание на траекторию, которую описывает центр масс стержня при соскальзывании. Если стержень касается своими концами и стенки, и пола, то центр масс движется по дуге с радиусом R = L/2, показанной на рис. 4, слева. Если стержень касается только пола, то центр масс может находиться где угодно справа от дуги. Забраться «под дугу» центр масс не может никак. Поэтому исходная задача — соскальзывание стержня вдоль стенки, а затем отрыв от нее — с точки зрения движения центра масс выглядит так: центр масс без трения скользит по полукруглому холму и в какой-то момент срывается с него (см. рис. 4, справа).
Для того чтобы эта словесная аналогия стала полным математическим эквивалентом, перепишем потенциальную и кинетическую энергию стержня в исходной задаче
через массу центра масс (mcm = 2m), горизонтальную (vx = vB/2) и вертикальную (vy = vA/2) скорости центра масс, а также его высоту:
Обратите внимание на лишнюю двойку в кинетической энергии; она возникла потому, что кроме движения центра масс стержень еще и вращается, и в нашем простом случае кинетическая энергия вращения равна кинетической энергии движения центра масс. Это означает, что задачу нельзя просто так сводить к движению центра масс. Однако если переписать эти энергии вот так
где M = 2mcm = 4m, а = g/2, а скорость
то все формулы становятся привычными. Таким образом, мы приходим к выводу: наша задача математически эквивалентна задаче о скольжении одной-единственной материальной точки с массой M = 4m по полукруглому холму радиуса R = L/2 в ослабленном поле тяжести с ускорением свободного падения a = g/2. Всё это происходит также под действием дополнительной горизонтальной силы (аналог Four), которая обеспечивает постоянство горизонтальной скорости точки (vx = v/2). Из геометрии видно, что тот угол α, при котором точка срывается с холма, как раз равен углу, при котором стержень отрывается от стенки в исходной задаче. Этот угол и требуется найти.
Эту задачу решить уже несложно. Для того чтобы тело массы M двигалось по окружности радиуса R со скоростью u, надо, чтобы центростремительная сила равнялась Mu 2 /R. Эта сила в нашем случае складывается из проекции силы тяжести Ma·sin α, а также силы реакции опоры и проекции силы Four. В момент отрыва две последние силы исчезают, и это позволяет нам наконец-то записать условие на угол α:
Поскольку синус не бывает больше единицы, а v и L задаются в условии независимо, мы получаем два разветвления задачи: если скорость велика, отрыв произойдет сразу же, и дальше стержень будет падать свободно. Если же скорость достаточно мала (что и предполагалось в условии), то отрыв произойдет не сразу, а при угле α, задаваемом найденной формулой. Стоит также отметить, что ту же самую формулу можно было найти, рассматривая исходную задачу в системе отсчета точки B (рис. 2, справа) и записав центростремительное ускорение для точки A
Шаг 4. Осталось обсчитать свободное падение стержня с начального угла α. Проще всего это сделать, вновь перейдя в (инерциальную) систему отсчета, где точка B покоится (рис. 2, справа, но только без стенки). В этой системе отсчета сила Four приложена к неподвижной точке, и поэтому она работы не совершает. Значит, в этой системе отсчета можно воспользоваться законом сохранения энергии:
Скорость u1 — это (вертикальная) скорость точки A в этой системе отсчета в момент удара об пол. Возвращаясь обратно в исходную систему отсчета, получаем окончательный ответ:
Послесловие
Получив в самом начале бесконечность, мы удивились несоответствию этого ответа тем усилиям, которые нужно затратить для экспериментальной реализации такой ситуации. Потом мы, правда, поняли, что этот бесконечный ответ получается из-за предположения, что контакт со стенкой остается до самого конца — предположения, ошибочного для нашей задачи.
Но ведь мы можем рассмотреть и другую задачу, в которой верхний конец стержня действительно физически прикреплен к стенке так, что он может скользить вдоль нее, но не может оторваться. Такая ситуация кажется вполне реализуемой экспериментально. Так как же в этом случае понимать бесконечный ответ? Над этим вопросом я предлагаю читателям подумать самостоятельно.
В заключение я хочу отдельно поговорить про тот прием, который мы использовали в решении задачи на шаге 3. В физике часто бывает так, что совсем разные физические задачи описываются одинаково с точки зрения математики. В нашем примере это были две механические системы, визуально совершенно непохожие друг на друга: первая — это стержень, опирающийся на стенку и ровный пол, вторая — это точка, скользящая по круглому холму, да к тому же в условиях ослабленной гравитации. Однако мы установили между ними «математический мостик», и благодаря ему решение второй задачи автоматически дало решение первой.
Тут надо понимать, что этой второй механической системы в реальности не было. Нет смысла спрашивать: а где на самом деле находится эта странная точка с массой M = 4m и с чего это ускорение свободного падения уменьшилось вдвое? Это был как бы виртуальный мир, который мы построили сами и в котором исходная задача преломилась под новым углом зрения.
Стержень длиной l и массой m одним концом упирается в вертикальную стенку
Стержень длиной \(l\) и массой \(m\) одним концом упирается в вертикальную стенку, а другой его конец удерживается нитью, длина которой равна длине стержня. При каком угле \(\alpha\) стержень будет находиться в равновесии, если коэффициент трения между стержнем и стеной равен 0,3?
Задача №3.1.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Решение задачи:
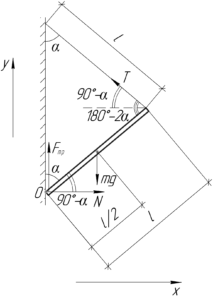
Покажем на схеме все силы, которые действуют на стержень: это сила тяжести стержня \(mg\), сила натяжения нити \(T\) и компоненты реакции опоры в точке O – сила нормальной реакции \(N\) и сила трения \(F_\). Стержень находится в равновесии, поэтому мы можем записать первое условие равновесия в проекции на оси \(x\) и \(y\) (первый закон Ньютона) и второе условие равновесия относительно точки O (правило моментов). Все необходимые для определения проекций и плеч сил углы показаны на схеме.
\[\left\< \begin
> + T \cdot \sin \left( \right) – mg = 0 \hfill \\
T \cdot \cos \left( \right) = N \hfill \\
mg \cdot \frac \cdot \cos \left( \right) – T \cdot l \cdot \sin \left( \right) = 0 \hfill \\
\end \right.\]
Из тригонометрии известно, что \(\cos \alpha = \sin \left( \right)\), \(\sin \alpha = \cos \left( \right)\) и \(\sin 2\alpha = \sin \left( \right)\), поэтому:
\[\left\< \begin
> + T \cdot \cos \alpha – mg = 0 \;\;\;\;(1)\hfill \\
T \cdot \sin \alpha = N \;\;\;\;(2)\hfill \\
mg \cdot \frac \cdot \sin \alpha – T \cdot l \cdot \sin 2\alpha = 0 \;\;\;\;(3)\hfill \\
\end \right.\]
Поработаем над равенством (3). Так как \(\sin 2\alpha = 2\sin \alpha \cdot \cos \alpha\), то:
\[mg \cdot \frac \cdot \sin \alpha – T \cdot l \cdot 2\sin \alpha \cdot \cos \alpha = 0\]
\[\frac> – 2T \cdot \cos \alpha = 0\]
\[mg = 4T \cdot \cos \alpha \;\;\;\;(4)\]
Преобразуем равенство (2) в такой вид:
Из равенства (1) выразим силу трения \(F_\):
\[> = mg – T \cdot \cos \alpha \]
Учитывая ранее полученное равенство (4), имеем:
\[> = 4T \cdot \cos \alpha – T \cdot \cos \alpha = 3T \cdot \cos \alpha \]
Стержень будет оставаться в равновесии, пока имеет место сила трения покоя, т.е. справедливо неравенство:
Произведем математические преобразования:
Минимальное значение угла \(\alpha\), при котором возможно равновесие, равно:
Ответ: 1,47 рад.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
Ошибка в четвертой формуле. Должно быть mg=4T*2cosA, т.к. все множители должны домножиться на 2, а не только первый. Или я не прав?
Не правы.\[\frac> – 2T \cdot \cos \alpha = 0\]\[\frac> = 2T \cdot \cos \alpha \]\[mg = 4T \cdot \cos \alpha \]
А если стержень подвязан в центре и имеет длину в два раза меньше, чем у нити. Каким будет решение? Заранее спасибо
В следующий раз, пожалуйста, приводите полное условие задачи. Рисунок прикрепить в комментарии возможности не имею, но он практически такой же, как в решении, приведенном сверху (ну разве что стержень подвешен за середину). Угол между стержнем и стеной обозначу за \(\alpha\), а между нитью и стеной – \(\beta\). Запишем два условия равновесия (аналогично как в решении выше):\[\left\< \beginT\sin \beta = N \hfill \\
T\cos \beta + > = mg \hfill \\
T\sin \left( \right) \cdot \frac = mg\sin \alpha \cdot \frac \hfill \\
\end \right.\]
Тогда:\[\left\< \begin
T\sin \beta = N \hfill \\
> = mg – T\cos \beta \hfill \\
\frac <
\end \right.\]
Стержень будет оставаться в равновесии, пока имеет место сила трения покоя, т.е. справедливо неравенство:
\[> \leq \mu N\]Поэтому:\[\frac <
Читайте также:
