Удельное сопротивление стального провода
Данная статья поможет вам рассчитать сопротивление кабеля. Расчет можно выполнить по формулам, либо по данным таблицы "сопротивление кабелей",которая приведена ниже.
То как влияет материал проводника учитывается при помощи удельного сопротивления, которое принято обозначать буквой греческого алфавита ρ и являет собой сопротивление проводника сечением 1 мм2 и длинной 1м. У серебра наименьшее удельное сопротивление ρ = 0,016 Ом•мм2/м. Ниже приводятся значения удельного сопротивления для нескольких проводников:
- Сопротивление кабеля для серебра - 0,016,
- Сопротивление кабеля для свинеца - 0,21,
- Сопротивление кабеля для меди - 0,017,
- Сопротивление кабеля для никелина - 0,42,
- Сопротивление кабеля для люминия - 0,026,
- Сопротивление кабеля для манганина - 0,42,
- Сопротивление кабеля для вольфрама - 0,055,
- Сопротивление кабеля для константана - 0,5,
- Сопротивление кабеля для цинка - 0,06,
- Сопротивление кабеля для ртути - 0,96,
- Сопротивление кабеля для латуни - 0,07,
- Сопротивление кабеля для нихрома - 1,05,
- Сопротивление кабеля для стали - 0,1,
- Сопротивление кабеля для фехрали -1,2,
- Сопротивление кабеля для бронзы фосфористой - 0,11,
- Сопротивление кабеля для хромаля - 1,45
Так как в состав сплавов входят разные количества примесей, то удельное сопротивление может изменятся.
Для расчёта сопротивления проводника вы можете воспользоваться калькулятором расчета сопротивления проводника.
Сопротивление кабеля рассчитывается по формуле,которая приведена ниже:
- R — сопротивление,
- Ом; ρ — удельное сопротивление, (Ом•мм2)/м;
- l — длина провода, м;
- s — площадь сечения провода, мм2.
Площадь сечения рассчитывается так:
S=(π?d^2)/4=0.78?d^2≈0.8?d^2
Измерить диаметр провода можно микрометром либо штангенциркулем,но если их нету под рукой,то можно плотно намотать на ручку (карандаш) около 20 витков провода, затем измерить длину намотанного провода и разделить на количество витков.
Для определения длинны кабеля,которая нужна для достижения необходимого сопротивления,можно использовать формулу:

1.Если данные для провода отсутствуют в таблице,то берется некоторое среднее значение.Как пример ,провод из никелина который имеет диаметр 0,18 мм площадь сечения равна приблизительно 0,025 мм2, сопротивление одного метра 18 Ом, а допустимый ток 0,075 А.
2.Данные последнего столбца,для другой плотности тока, необходимо изменить. Например при плотности тока 6 А/мм2, значение необходимо увеличить вдвое.
Пример 1. Давайте найдем сопротивление 30 м медного провода диаметром 0,1 мм.
Решение. С помощью таблицы берем сопротивление 1 м медного провода, которое равно 2,2 Ом. Значит, сопротивление 30 м провода будет R = 30•2,2 = 66 Ом.
Расчет по формулам будет выглядеть так: площадь сечения : s= 0,78•0,12 = 0,0078 мм2. Поскольку удельное сопротивление меди ρ = 0,017 (Ом•мм2)/м, то получим R = 0,017•30/0,0078 = 65,50м.
Пример 2. Сколько провода из манганина у которого диаметр 0,5 мм нужно чтобы изготовить реостат, сопротивлением 40 Ом?
Решение. По таблице выбираем сопротивление 1 м этого провода: R= 2,12 Ом: Чтобы изготовить реостат сопротивлением 40 Ом, нужен провод, длина которого l= 40/2,12=18,9 м.
Расчет по формулам будет выглядеть так. Площадь сечения провода s= 0,78•0,52 = 0,195 мм2. Длина провода l = 0,195•40/0,42 = 18,6 м.
Электропроводность: объяснение, формулы, единица измерения, таблица
Почему медь проводит электричество лучше, чем вода? Прочитав эту статью, вы больше не будете задавать себе больше этот вопрос. Далее мы обсудим электропроводность и рассмотрим формулы, которые описывают это понятие. Наконец, вы можете проверить свои знания на двух примерах.
Простое объяснение.
Электропроводность – это физическая величина, которая описывает насколько хорошо определенный материал проводит электричество.
Формулы
Существует три различных формульных обозначения удельной электропроводности σ (греч. сигма), k (каппа) и γ (гамма). В дальнейшем мы будем использовать σ. Формула электропроводности, также называемой удельной электропроводностью, описывается формулой:
σ = 1 / ρ .
Здесь ρ называется удельным сопротивлением. Вы можете рассчитать электрическое сопротивление R проводника с учетом его параметров следующим образом: R = ( ρ * l ) / S .
Таким образом, сопротивление R равно удельному сопротивлению ρ , умноженному на длину проводника l, деленному на площадь поперечного сечения S. Если теперь вы хотите выразить эту формулу через удельную электропроводность σ = 1 / ρ , полезно знать, что электрическая проводимость G проводника выражается следующим образом: G = 1 / R .
Если в верхнюю формулу подставить удельную электропроводность σ и электрическую проводимость G, то получится следующее: 1 / G = ( 1 / σ ) * ( l / S ) .
Путем дальнейшего преобразования можно получить выражение: G = σ * S / l .
С помощью электропроводности можно также описать важную зависимость между плотностью электрического тока и напряженностью электрического поля с помощью выражения: J = σ * E .
Единица измерения
Единицей удельной электропроводности σ в СИ является: [ σ ] = 1 См/м ( Сименс на метр ).
Эти единицы определяются по формуле G = σ * S / l . Если решить эту формулу в соответствии с σ, то получим σ = G * l / S .
Единица измерения электрической проводимости G задается как: [ G ] = 1 / σ = 1 См ( Сименс, международное обозначение: S ).
Если теперь ввести в формулу все единицы измерения, то получится:
[ σ ] = 1 См * 1 м / м 2 = 1 См / м .
Вы также будете чаще использовать единицы измерения См / см , м / Ом * мм 2 или См * м / мм 2 . Вы можете преобразовать отдельные измеряемые переменные так: См / см = См / 10 -2 м и так: м / Ом * мм 2 = См * м / мм 2 = См * м / 10 -3 м * 10 -3 м = 10 6 См / м .
Электропроводность металлов
В зависимости от количества свободно перемещающихся электронов один материал проводит лучше, чем другой. В принципе, любой материал является проводящим, но в изоляторах, например, протекающий электрический ток ничтожно мал, поэтому здесь мы говорим о непроводниках.
В металлических связях валентные электроны, т.е. крайние электроны в атоме, свободно подвижны. Они расположены в так называемой полосе проводимости. Находящиеся там электроны образуют так называемый электронный газ. Соответственно, металлы являются сравнительно хорошими проводниками. Если теперь подать электрическое напряжение на металл, валентные электроны медленно движутся к положительному полюсу, потому что он их притягивает.

Рис. 1. Движение электронов в металле
На рисунке 1 видно, что некоторые электроны не могут быть притянуты непосредственно к положительному полюсу, потому что на пути стоит, так сказать, твердое атомное ядро. Там они замедляются и в некоторой степени отклоняются. Именно поэтому электроны не могут ускоряться в металле бесконечно, и именно так возникает удельное сопротивление или электропроводность.
Теперь вы также можете измерить удельную электропроводность в металле с помощью следующей формулы: σ = ( n * e 2 * τ ) / m .
В этой формуле n означает число электронов, e – заряд электрона, m – массу электрона, а τ – среднее время полета электрона между двумя столкновениями.
Таблица удельной электропроводности
Для большинства веществ уже известны значения удельной электропроводности. Некоторые из них вы можете найти в следующей таблице ниже. Все значения в этой таблице действительны для комнатной температуры, т.е. 25°C.
| Вещество | Удельная электропроводность в См / м |
| Серебро | 62 · 10 6 |
| Медь | 58 · 10 6 |
| Золото | 45,2 · 10 6 |
| Алюминий | 37,7 · 10 6 |
| Вольфрам | 19 · 10 6 |
| Латунь | 15,5 · 10 6 |
| Железо | 9,93 · 10 6 |
| Нержавеющая сталь (WNr. 1,4301) | 1,36 · 10 6 |
| Германий (легирование | 2 |
| Кремний (легирование | 0,5 · 10 -3 |
| Морская вода | примерно 5 |
| Водопроводная вода | примерно 0,05 |
| Дистиллированная вода | 5 · 10 -6 |
| Изолятор | обычно |
Удельная электропроводность сильно зависит от температуры, поэтому указанные значения применимы только при 25°C. При повышении температуры вибрация решетки в веществе становится выше. Это нарушает поток электронов, и поэтому электропроводность уменьшается с ростом температуры.
Из таблицы видно, что медь имеет вторую по величине электропроводность, поэтому медные кабели очень часто используются в электротехнике. Серебро обладает еще более высокой проводимостью, но стоит намного дороже меди.
Интересно также сравнение между морской и дистиллированной водой. Здесь электропроводность возникает благодаря растворенным в воде ионам. Морская вода имеет очень высокую долю соли, которая растворяется в воде. Эти ионы передают электрический ток. В дистиллированной воде нет растворенных ионов, поэтому в ней практически не может протекать электрический ток. Поэтому электропроводность морской воды намного выше, чем дистиллированной.
Примеры задач
Для более детального рассмотрения приведём два примера расчетов.
В первой задаче представьте, что у вас есть провод длиной 2 м с поперечным сечением 0,5 мм 2 . Электрическое сопротивление провода при комнатной температуре составляет 106 мОм. Из какого материала изготовлен провод?
Решение данной задачи можно найти с помощью формулы: R = ( 1 / σ ) * ( l / S ). Из этой формулы найдём σ = l / ( S * R ) .
Теперь вы можете вставить заданные значения, убедившись, что вы перевели сечение в м 2 .
σ = l / ( S * R ) = 2 м / ( ( 0,5 * 10 -6 м 2 ) * ( 1 / 106 * 10 -3 Ом ) ) = 37, 7 * 10 6 См / м .
Наконец, вы ищите в таблице, какой материал имеет удельную электропроводность σ = 37, 7 * 10 6 См / м и приходите к выводу, что провод сделан из алюминия.
В задаче 2 вам дано только удельное сопротивление образца с 735 * 10 -9 Ом * м. Из какого материла изготовлен образец?
Вы можете использовать формулу σ = 1 / ρ для расчёта удельной электропроводности. После подстановки значений в эту формулу вы получите: σ = 1 / ρ = 1 / 735 * 10 -9 Ом * м = 1,36 * 10 6 См / м .
Если вы снова заглянете в таблицу, то обнаружите, что образец должен быть изготовлен из нержавеющей стали.
Удельное сопротивление для распространенных материалов: таблица
Приведенная ниже таблица удельного электрического сопротивления содержит значения удельного сопротивления для многих веществ, широко используемых в электрике и электронике. В частности, она включает в себя удельное сопротивление меди, алюминия, нихрома, стали, никеля и так далее.
Удельное электрическое сопротивление особенно важно, поскольку оно определяет электрические характеристики и, следовательно, пригодность материала для использования во многих электрических компонентах. Например, можно увидеть, что удельное сопротивление меди, удельное сопротивление алюминия, а также нихрома, никеля, серебра, золота и т.д. определяет, где эти металлы используются.
Для того чтобы сравнить способность различных материалов проводить электрический ток, используются показатели удельного сопротивления.
Что означают показатели удельного сопротивления?
Для того чтобы иметь возможность сравнивать удельное сопротивление различных материалов, от таких изделий, как медь и алюминий, до других металлов и веществ, включая висмут, латунь и даже полупроводники, необходимо использовать стандартное измерение.
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом·м.
Единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м 2 , изготовленный из этого вещества, имеет сопротивление, равное 1 Ом. Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 м 2
[1]
Таблица удельного сопротивления для распространенных проводников
В таблице ниже приведены показатели удельного сопротивления для различных материалов, в частности металлов, используемых для электропроводности.
Показатели удельного сопротивления приведены для таких “популярных” материалов, как медь, алюминий, нихром, сталь, свинец, золото и других.
| Материал | Удельное сопротивление, ρ, при 20 °C (Ом·м) | Источник |
|---|---|---|
| Латунь | ~0.6 – 0.9 x 10 -7 | |
| Серебро | 1.59×10 −8 | [3][4] |
| Медь | 1.68×10 −8 | [5][6] |
| Обожжённая медь | 1.72×10 −8 | [7] |
| Золото | 2.44×10 −8 | [3] |
| Алюминий | 2.65×10 −8 | [3] |
| Кальций | 3.36×10 −8 | |
| Вольфрам | 5.60×10 −8 | [3] |
| Цинк | 5.90×10 −8 | |
| Кобальт | 6.24×10 −8 | |
| Никель | 6.99×10 −8 | |
| Рутений | 7.10×10 −8 | |
| Литий | 9.28×10 −8 | |
| Железо | 9.70×10 −8 | [3] |
| Платина | 1.06×10 −7 | [3] |
| Олово | 1.09×10 −7 | |
| Тантал | 1.3×10 −7 | |
| Галлий | 1.40×10 −7 | |
| Ниобий | 1.40×10 −7 | [8] |
| Углеродистая сталь (1010) | 1.43×10 −7 | [9] |
| Свинец | 2.20×10 −7 | [2][3] |
| Галинстан | 2.89×10 −7 | [10] |
| Титан | 4.20×10 −7 | |
| Электротехническая сталь | 4.60×10 −7 | [11] |
| Манганин (сплав) | 4.82×10 −7 | [2] |
| Константан (сплав) | 4.90×10 −7 | [2] |
| Нержавеющая сталь | 6.90×10 −7 | |
| Ртуть | 9.80×10 −7 | [2] |
| Марганец | 1.44×10 −6 | |
| Нихром (сплав) | 1.10×10 −6 | [2][3] |
| Углерод (аморфный) | 5×10 −4 – 8×10 −4 | [3] |
| Углерод (графит) параллельно-базальная плоскость | 2.5×10 −6 – 5.0×10 −6 | |
| Углерод (графит) перпендикулярно-базальная плоскость | 3×10 −3 | |
| Арсенид галлия | 10 −3 to 10 8 | |
| Германий | 4.6×10 −1 | [3][4] |
| Морская вода | 2.1×10 −1 | |
| Вода в плавательном бассейне | 3.3×10 −1 – 4.0×10 −1 | |
| Питьевая вода | 2×10 1 – 2×10 3 | |
| Кремний | 2.3×10 3 | [2][3] |
| Древесина (влажная) | 10 3 – 10 4 | |
| Деионизированная вода | 1.8×10 5 | |
| Стекло | 10 11 – 10 15 | [3][4] |
| Углерод (алмаз) | 10 12 | |
| Твердая резина | 10 13 | [3] |
| Воздух | 10 9 – 10 15 | |
| Древесина (сухая) | 10 14 – 10 16 | |
| Сера | 10 15 | [3] |
| Плавленый кварц | 7.5×10 17 | [3] |
| ПЭТ | 10 21 | |
| Тефлон | 10 23 – 10 25 |
Видно, что удельное сопротивление меди и удельное сопротивление латуни оба низкие, и с учетом их стоимости, относительно серебра и золота, они становятся экономически эффективными материалами для использования для многих проводов. Удельное сопротивление меди и простота ее использования привели к тому, что она также используется крайне часто в качестве материала для проводников на печатных платах.
Изредка алюминий и особенно медь используются из-за их низкого удельного сопротивления. Большинство проводов, используемых в наши дни для межсоединений, изготовлены из меди, поскольку она обеспечивает низкий уровень удельного сопротивления при приемлемой стоимости.
Удельное сопротивление золота также важно, поскольку золото используется в некоторых критических областях, несмотря на его стоимость. Часто золотое покрытие встречается на высококачественных слаботочных разъемах, где оно обеспечивает самое низкое сопротивление контактов. Золотое покрытие очень тонкое, но даже в этом случае оно способно обеспечить требуемые характеристики разъемов.
Серебро имеет очень низкий уровень удельного сопротивления, но оно не так широко используется из-за его стоимости и из-за того, что оно тускнеет, что может привести к более высокому сопротивлению контактов.
Однако оно используется в некоторых катушках для радиопередатчиков, где низкое удельное электрическое сопротивление серебра снижает потери. При использовании в таких целях серебро обычно наносилось только на существующий медный провод. Покрытие провода серебром позволило значительно снизить затраты по сравнению с цельным серебряным проводом без существенного снижения производительности.
Другие материалы в таблице удельного электрического сопротивления могут не иметь такого очевидного применения. Тантал фигурирует в таблице, поскольку используется в конденсаторах – никель и палладий используются в торцевых соединениях многих компонентов поверхностного монтажа, таких как конденсаторы.
Кварц находит свое основное применение в качестве пьезоэлектрического резонансного элемента. Кварцевые кристаллы используются в качестве частотоопределяющих элементов во многих осцилляторах, где высокое значение Q позволяет создавать очень стабильные по частоте схемы. Аналогичным образом они используются в высокоэффективных фильтрах. Кварц имеет очень высокий уровень удельного сопротивления и не является хорошим проводником электричества, то есть его относят к категории диэлектрикам.
Удельное сопротивление стального провода
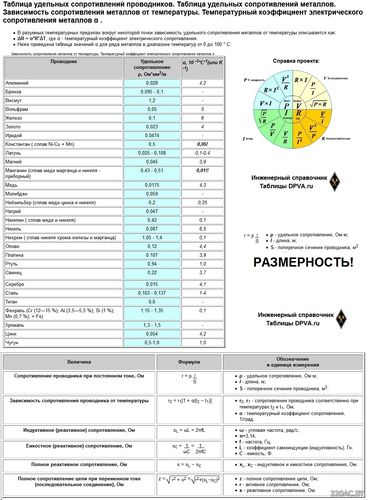
Нажмите на изображение чтобы увеличить.
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих закона Ома, выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный резистор, изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)
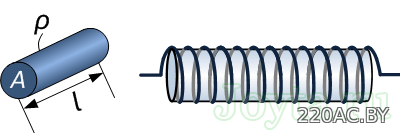
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
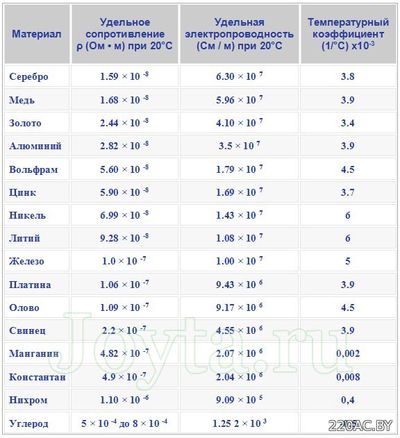
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко поддается пайке и имеет более низкий температурный коэффициент.
Сопротивление провода.
Данная статья поможет вам рассчитать сопротивление провода. Расчет можно выполнить по формулам, либо по данным таблицы "сопротивление проводов", которая приведена ниже.
То как влияет материал проводника учитывается при помощи удельного сопротивления, которое принято обозначать буквой греческого алфавита ρ и являет собой сопротивление проводника сечением 1 мм 2 и длинной 1 м. У серебра наименьшее удельное сопротивление ρ = 0,016 Ом•мм 2 /м. Ниже приводятся значения удельного сопротивления для нескольких проводников:
- Сопротивление провода для серебра - 0,016,
- Сопротивление провода для свинеца - 0,21,
- Сопротивление провода для меди - 0,017,
- Сопротивление провода для никелина - 0,42,
- Сопротивление провода для люминия - 0,026,
- Сопротивление провода для манганина - 0,42,
- Сопротивление провода для вольфрама - 0,055,
- Сопротивление провода для константана - 0,5,
- Сопротивление провода для цинка - 0,06,
- Сопротивление провода для ртути - 0,96,
- Сопротивление провода для латуни - 0,07,
- Сопротивление провода для нихрома - 1,05,
- Сопротивление провода для стали - 0,1,
- Сопротивление провода для фехрали -1,2,
- Сопротивление провода для бронзы фосфористой - 0,11,
- Сопротивление провода для хромаля - 1,45
Сопротивление провода рассчитывается по формуле,которая приведена ниже:
- R — сопротивление,
- Ом; ρ — удельное сопротивление, (Ом•мм 2 )/м;
- l — длина провода, м;
- s — площадь сечения провода, мм 2 .
Для определения длинны провода,которая нужна для достижения необходимого сопротивления,можно использовать формулу:
Расчет по формулам будет выглядеть так. Площадь сечения провода s= 0,78•0,52 = 0,195 мм 2 . Длина провода l = 0,195•40/0,42 = 18,6 м.
Читайте также:
