Теплопередача через стальную стенку
Под теплопередачей через стенку понимают процесс передачи теплоты между двумя средами через непроницаемую стенку любой геометрической формы в стационарном и нестационарном режимах теплообмена. Стенка может быть многослойной.
Рассмотрим стационарный режим теплопередачи через плоскую, цилиндрическую и сферическую стенки при котором теплопередача - величина постоянная и температурное поле не изменяется во времени и зависит только от координаты. В этом случае при условии постоянства теплофизических свойств тела температура в плоской стенке изменяется линейно, а в цилиндрической - по логарифмическому закону, т.е.
Q = const и T = f(x) - линейная (при плоской стенке) или логарифмическая функция (при круглой стенке).
Согласно второму закону термодинамики процесс теплопередачи идет от среды с большей температурой к среде с меньшей температурой.
Теплопередача через непроницаемую стенку включает в себя следующие процессы:
- теплоотдачу от горячей среды к стенке;
- теплопроводность внутри стенки;
- теплоотдачу от стенки к холодной среде.
Теплопередача через плоскую стенку (граничные условия первого рода)
Теплопроводность - первое элементарное тепловое явление переноса теплоты посредством теплового движения микрочастиц в сплошной среде, обусловленное неоднородным распределением температуры.
Совокупность значений температуры для всех точек пространства в данный момент времени называется температурным полем.
Если температурное поле не изменяется во времени, то мы имеем дело со стационарным тепловым режимом.
Тепловой поток Q [Вт] - это количество теплоты, передаваемой в единицу времени (1 Дж/с=1 Вт).
Поверхностная плотность теплового потока рассчитывается по формуле:
где Q - тепловой поток [Вт]; F - площадь стенки [м 2 ].
На основании закона Фурье q=-λdT/dx, значение плотности теплового потока для однослойной стенки будет определяться по формуле:
где δ = dx - толщина стенки, λ
λ/δ; [Вт/м 2 *К] - коэфициент тепловой проводности стенки.
а обратная величина -
R = δ/λ; [м 2. К/Вт] - термическое сопротивление стенки.
Для теплового потока формулу так же можно представить в виде:
Общее количество теплоты проходящее через площадь стены S за время t можно представить как:
Распределение температуры в плоской стенке
Рассмотрим изменение температуры в нашей стене. Так как у нас тепловой поток постоянный, то dT/dx = const=C1; T=C1х+С2 (1). Определим С1 и С2 через граничные условия.
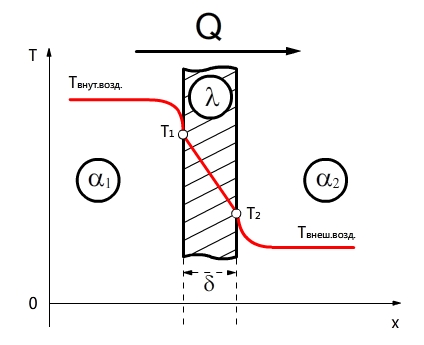
При х=0 T=T1, подставим в уравнение (1) и получим T1=С2.
При х=δ T=T2, подставим в уравнение (1) и получим T2=С1*δ+С2, T2=С1*δ+T1, получим: С1=(Т2-T1)/δ. Теперь подставим в уравнение (1) найденные С1 и С2, получим следующее распределение температуры в нашей стене:
Если нам нужно узнать на какой глубине стены Т=То, то формула преобразуется в следующий вид:
Теплопроводность через многослойную стенку
Если у нас есть стенка из нескольких (n) слоев с разными коэффициентами теплопроводности λi и разной толщиной δi.
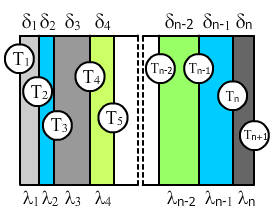
Термическое сопротивление стенки считается так:
Для теплового потока формула будет иметь вид:
Температура на границе слоя вычисляется по следующей формуле:
Например, если нужно вычислить температуру между 3-м и 4-м слоем, формула будет такая:
Эквивалентная теплопроводность многослойной стенки:
Теплопередача через плоскую стенку в граничащую среду (граничные условия третьего рода)
Теплопередача - это более сложный процесс теплообмена между жидкими и газообразными средами, разделенными твердой стенкой. Теплопередача включает в себя и процесс теплопроводности, и процесс теплоотдачи.
Коэффициент теплоотдачи α, Вт/(м 2 ·К) - это количество теплоты, отдаваемое в единицу времени единицей поверхности при разности температур между поверхностью и окружающей средой, равной одному градусу.
Коэффициент теплопередачи k, Вт/(м 2 ·К), характеризует тепловой поток, проходящий через единицу площади поверхности стенки при разности температуры сред, равной одному градусу:
q = k * (Tвозд.внутри - Tвозд.снаружи); Вт/м 2
Коэффициент теплопередачи для n слойной стенки:
Термические сопротивления теплоотдаче на внешних поверхностях стенки будут равны:
Тогда общее термическое сопротивление теплопередаче будет равно:
Температуры на поверхности стенки можно определить по формулам:
Теплопроводность через цилиндрическую стенку (граничные условия первого рода)
Теплообменные аппараты в большинстве случаев имеют не плоские, а цилиндрические поверхности, например рекуператоры типа "труба в трубе", кожухотрубные водонагреватели и т.д. Поэтому возникает необходимость рассмотрения основных принципов расчета цилиндрических поверхностей.
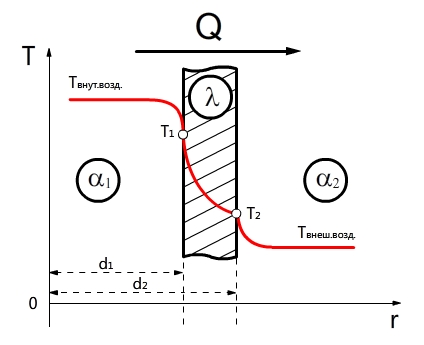
Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:
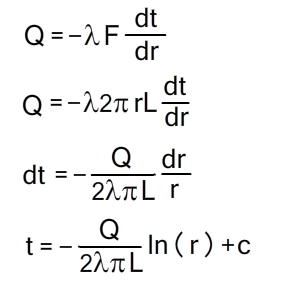
Подставим значения граничные значение и вспомним, что разность логарифмов равна логарифму отношению аргументов, получим:
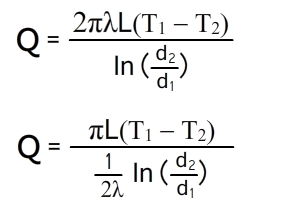
Распределение температур внутри однородной цилиндрической стенки подчиняется логарифмическому закону, и уравнение температурной кривой имеет вид:
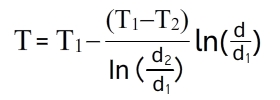
Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины трубы L, либо к единице внутренней F1 или внешней F2 поверхности трубы. При этом расчетные формулы принимают следующий вид:
Все материалы, представленные на сайте, носят исключительно справочный и ознакомительный характер и не могут считаться прямой инструкцией к применению. Каждая ситуация является индивидуальной и требует своих расчетов, после которых нужно выбирать нужные технологии.
Не принимайте необдуманных решений. Имейте ввиду, что то что сработало у других, в ваших условиях может не сработать.
Администрация сайта и авторы статей не несут ответственности за любые убытки и последствия, которые могут возникнуть при использовании материалов сайта.
Теплопроводность через стенку
Решение. 1.а) стенка стальная, чистая, толщиной =14 мм, теплопроводность стали = 50 Вт/(м*К)
1.а) стенка стальная, чистая, толщиной = 50 Вт/(м*К).
Находим коэффициент теплопередачи стальной стенки k:
Термическое сопротивление сталиПлотность теплового потока в стальной стенке:
Величина теплового потока Q численно равна плотности теплового потока q, т.к. площадь поверхности F =1 и времяЭквивалентный коэффициент теплопроводности = 50 Вт/(м*К), т.к. стенка однослойная.
1. б) стенка медная, чистая, толщиной = 350 Вт/(м*К);
1.в) стенка стальная, со стороны воды покрыта слоем накипи = 2 Вт/(м*К);
1. г) стенка стальная, со стороны воды покрыта слоем накипи = 2 Вт/(м*К), поверх накипи имеется слой масла толщиной = 0,1 Вт/(м*К);
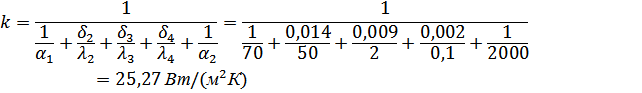
Коэффициент теплопередачи в такой многослойной стенке
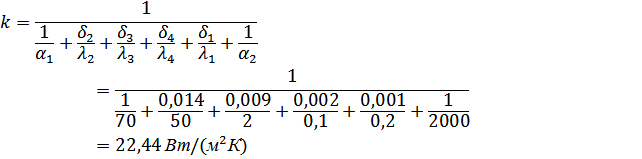
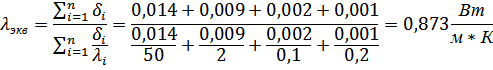
2. Примем плотность потока тепла для случая а) за 100%, подсчитаем плотности потоков тепла для остальных случаев:
3. Определим расчетным путем температуры всех поверхностей слоев стенки для случая д), для этого используем следующее уравнение:
а) температура на поверхности стенки со стороны газов
б) температура на границе между слоем сажи и сталью
в) температура на границе между стальной стенкой и слоем накипи
г) температура на границе между слоем накипи и слоем масла
д) температура на поверхности стенки со стороны воды
4. Проверим расчетные температуры графически.
Получили5. Построим для случая д) линию падения температуры в стенке.
Задание 2.Конвективный теплообмен и теплопередача через многослойную цилиндрическую стенку.
По горизонтальному стальному трубопроводу (рис.1), с внутренним и наружным диаметром соответственно D1 = 25мм и D2 = 32мм движется вода со средней скоростью wж1 = 0,03м/с. Средняя температура воды tж1 = 140 tж2 = 22 tст3 = 44 k1 (Вт/м 2 К), потери теплоты с одного погонного метра трубопровода ql (Вт/м), а также температуру наружной поверхности стального трубопровода tст2.
Рассчитать, целесообразно или нет применять в качестве теплоизоляционного материала асбест? Приводит ли асбестовая изоляция к уменьшению теплового потока с поверхности трубопровода?
Применять следующие упрощающие предположения:
- течение воды в трубопроводе термически стабилизированное;
- между наружной поверхностью стального трубопровода и внутренней поверхностью изоляции существует идеальный тепловой контакт;
- считать, что теплопроводность стали 1=50 Вт/м*К и асбеста 2= 0,12 Вт/м*К не зависит от температуры.
Наружный диаметр изоляции должен быть рассчитан с такой точностью, чтобы температура на наружной поверхности изоляции отличалась от заданной не более чем на 0,11. Определим режим течения жидкости
2. Найдем коэффициент теплоотдачи α1, для этого сначала рассчитаем число Нуссельта
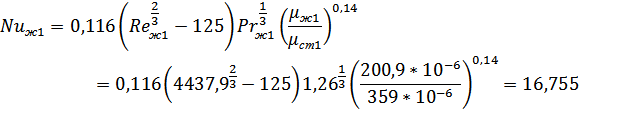
Т.к. температура стенки неизвестна, то в первом приближении задаемся значением
ст1=2,184
Отсюда 3. НайдемПервое приближение; теплообмен между наружной поверхностью изоляции и воздухом – это свободная конвекция. Для этого случая критериальное уравнение такое:
а)температурой воздуха и температурой поверхности изоляции:
б) труба расположена горизонтально и при свободной конвекции обтекается воздухом поперечно. При таком обтекании характерный размер – наружный диаметр изоляции, который пока неизвестен, поэтому в первом приближении будем считать4. Найдем наружный диаметр изоляции D3.
5. Определим линейный коэффициент теплопередачи от воды к воздуху:
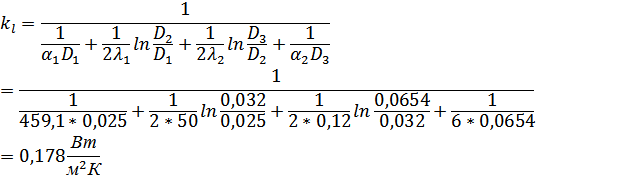
6. Определим потери теплоты с одного погонного метра трубопровода:
7. Определим температуру наружной поверхности стального трубопровода:
8. Рассчитаем эффективность асбестовой изоляции. Для этого найдем потери теплоты с неизолированного стального трубопровода:
и сравним его с найденной ранее величиной потерь с изолированного трубопровода. Очевидно, что изоляция асбестом в данном случае весьма эффективна.
Список рекомендуемой литературы
1. Транспортная энергетика: Учебник /Котиков Ю.Г., Ложкин В.Н. М.: Академия. – 2006 - 272 с.
2. Теплотехника: Учеб. для вузов /В.Н. Луканин, М.Г. Шатров, Г.М. Камодер и др.; Под ред. В.Н. Луканина. – 4-е изд., испр.. – М.: Высшая шк.. 2003 – 671 с.: ил.
Рабинович О. М. Сборник задач по технической термодинамике. Учебник для ВУЗов. – М.: «Машиностроение», 1973 – 348 с.
Теплопередача через стальную стенку
1. Однослойная плоская стенка. Имеется однородная плоская стенка с коэффициентом теплопроводности и толщиной . По одну сторону стенки находится горячая среда с температурой , по другую — холодная с температурой . Температуры поверхностей стенки неизвестны, обозначим их буквами (рис. 6-2). Задано значение суммарного коэффициента теплоотдачи на горячей стороне на холодной .
При установившемся тепловом состоянии количество теплоты, переданное от горячей жидкости к стенке, равно количеству теплоты, переданному через стенку, и количеству теплоты, отданному от стенки к холодной жидкости. Следовательно, для плотности теплового потока q можно написать три выражения:
Из этих уравнений определяются частные температурные напоры, а именно:
Складывая их, получаем полный температурный напор:
из которого определяется значение плотности теплового потока
и значение коэффициента теплопередачи
Рис. 6-2. Теплопередача через однослойную плоскую стенку; характер изменения температуры в теплоносителях и разделяющей их стенке.
Таким образом, чтобы вычислить значение коэффициента теплопередачи k для плоской стенки, необходимо знать толщину этой стенки , коэффициент теплопроводности и значения коэффициентов теплоотдачи .
Величина, обратная коэффициенту теплопередачи, называется общим термическим сопротивлением теплопередачи. Из уравнения (6-5) эта величина равна:
Из этого соотношения следует, что общее термическое сопротивление равно сумме частных:
где — частное термическое сопротивление теплоотдачи со стороны горячего теплоносителя; — частное термическое сопротивление теплопроводности (стенки); — частное термическое сопротивление теплоотдачи со стороны холодного теплоносителя.
2. Многослойная плоская стенка. Рассматривается стенка, состоящая из нескольких, например двух, слоев (рис. 6-3).
Толщины слоев и коэффициенты теплопроводности и . С одной стороны находится горячая среда с температурой , с другой — холодная с температурой . Значение суммарного коэффициента теплоотдачи с горячей стороны с холодной .
При установившемся тепловом состоянии системы плотность теплового потока постоянна и поэтому можно написать:
Из этих уравнений определяются частные температурные напоры:
Складывая раздельно левые и правые части уравнений, получаем полный температурный напор
и значение коэффициента теплопередачи для двухслойной плоской стенки
Распределение температур при теплопередаче через плоскую одно- и многослойную стенки представлено соответственно на рис. 6-2 и 6-3.
Неизвестные температуры могут быть определены из уравнений (е):
Если стенка состоит из нескольких слоев толщиной и коэффициенты теплопроводности их соответственно , то общее термическое сопротивление теплопередачи будет равно:
В этом случае уравнение (6-5) принимает вид:
Рис. 6-3. Теплопередача через многослойную плоскую стенку.
Температуры стенки можно определить и графически. Один из таких способов был описан в гл. 1. Поэтому мы здесь рассмотрим второй, который основан на замене термического сопротивления горячей и холодной среды термическим сопротивлением твердой стенки с таким же коэффициентом теплопроводности, как и действительная стенка.
Пусть температуры наружных поверхностей воображаемой стенки соответственно равны температурам горячей и холодной среды (рис. 6-4). Количество передаваемой теплоты остается без изменения. Тогда общая толщина этой воображаемой стенки определяется из соотношения
Здесь величины имеют размерность длины, м, они определяют собой эквивалентные толщины. При графическом построении сначала строится реальная стенка толщиной (в любом масштабе), затем по одну сторону от нее в том же масштабе откладывается значение а по другую — значение . Из крайних точек а и b по вертикали в некотором масштабе откладываются значения температур . Полученные точки А и С соединяются прямой линией. Точки пересечения этой прямой с поверхностями действительной стенки дают значения искомых температур .
Рис. 6-4. Графический способ определения температур на поверхности стенки.
Рис. 6-5. Графическое определение температуры на поверхности и в плоскости соприкосновения слоев двухслойной стенки.
Действительно, из подобия треугольников АВС и ADE имеем, что , откуда
Согласно уравнению (б) ; следовательно, отрезок . Таким же путем можно показать, что отрезок NG в выбранном масштабе температуры равен .
Если стенка многослойная и требуется определить лишь температуру наружных поверхностей, то построение производят точно таким же образом, как и для однослойной стенки, имея дело лишь со средним коэффициентом теплопроводности многослойной стенки (рис. 6-5).
Температура же между слоями в точке А определяется по пересечению двух лучей (способ построения виден из рис. 6-5).
Пример 6-1. Определить потерю теплоты через 1 м2 кирпичной обмуровки котла толщиной и температуры стенки , если температура газов 600° С, температура воздуха , коэффициент теплоотдачи со стороны газов , коэффициент теплоотдачи со стороны воздуха и коэффициент теплопроводности обмуровки .
Согласно уравнению (6-5)
Подставляя это значение в уравнение (6-4), имеем:
Наконец, из уравнения (б)
3. Однородная цилиндрическая стенка. Пусть имеется цилиндрическая стенка (труба) с внутренним диаметром внешним и длиной l. Стенка трубы однородна; ее коэффициент теплопроводности . Внутри трубы горячая среда с температурой , а снаружи — холодная с температурой . Температуры поверхностей стенки неизвестны, обозначим их через (рис. 6-6). Со стороны горячей среды суммарный коэффициент теплоотдачи а со стороны холодной .
При установившемся тепловом состоянии системы количество теплоты, отданное горячей и воспринятое холодной средой, одно и то же. Следовательно, можно написать:
Из этих соотношений определяем частные температурные напоры:
Складывая уравнения системы (к), получаем полный температурный напор
Рис. 6-6. Теплопередача через однослойную цилиндрическую стенку.
Рис. 6-7. Теплопередача через многослойную цилиндрическую стенку.
Из уравнения (л) определяется значение линейной плотности теплового потока
откуда линейный коэффициент теплопередачи (на длины трубы)
Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередачи.
Из уравнения (6-9) имеем:
Последнее означает, что общее термическое сопротивление равно сумме частных — термического сопротивления теплопроводности стенки и термических сопротивлений теплоотдачи . Значения определяются из уравнений (к).
4. Многослойная цилиндрическая стенка. В этом случае рассматривается передача теплоты через многослойную, например двухслойную, цилиндрическую стенку. Диаметры и коэффициенты теплопроводности отдельных слоев известны (рис. 6-7). Температура горячей среды холодной Коэффициент теплоотдачи со стороны горячей среды а со стороны холодной . Температуры поверхностей а также температура в месте соприкосновения разнородных цилиндрических слоев неизвестны.
При установившемся тепловом состоянии системы можно записать:
Определяем частные температурные напоры:
Складывая левые и правые части уравнений (н), получаем полный температурный напор
и значение линеинои плотности теплового потока
Распределение температур при теплопередаче через однослойную и многослойную цилиндрические стенки показано на рис. 6-6 и 6-7 соответственно.
Линейный коэффициент теплопередачи для двухслойной стенки
а общее термическое сопротивление .
Для многослойной стенки трубы
Чтобы определить неизвестные температуры стенки надо значение из уравнения (6-10) подставить в уравнения (н). Решая их, получаем:
Способ определения температуры между слоями описан в гл. 1. Расчетные формулы теплопередачи для труб довольно громоздки, поэтому при практических расчетах применяются некоторые упрощения. Если толщина стенки не очень велика, то вместо формулы (6-8) в расчетах применяется формула для плоской стенки (6-4), которая в этом случае (в применении к трубе длиной 1 м) принимает вид:
где k — коэффициент теплопередачи для плоской стенки, рассчитанный по формуле (6-5), dx — средний диаметр стенки; — ее толщина, равная полуразности диаметров.
При этом если , то погрешность расчета не превышает 4%. Эта погрешность снижается, если при выборе соблюдать следующее правило:
т. е. при расчете теплопередачи по формуле (6-12) вместо берется тот диаметр, со стороны которого коэффициент теплоотдачи имеет меньшее значение. Если же значения коэффициентов теплоотдачи одного порядка, то равно среднеарифметическому между внутренним и внешним диаметрами трубы. При проведении расчетов как по формуле (6-8), так и по формуле (6-12) всегда следует иметь в виду, что в целях упрощения расчета относительно малыми сопротивлениями можно и следует пренебрегать.
Пример 6-2. Паропровод диаметром 200/216 мм покрыт слоем совелитовой изоляции толщиной 120 мм, коэффициент теплопроводности которой . Температура пара и окружающего воздуха . Кроме того, заданы коэффициент теплопроводности стенки . Требуется определить линейный коэффициент теплопередачи, линейную плотность теплового потока и температуру в месте соприкосновения паропровода с изоляцией.
Согласно условию задачи . Далее на основании формулы (6-9) имеем:
Первые два члена общего термического сопротивления по сравнению с остальными малы, при расчетах ими можно было бы пренебречь. На основании формулы (5-8)
И, наконец, согласно формуле (н):
5. Шар. Пусть внутренний диаметр шара равен внешний и коэффициент теплопроводности стенки . Внутри шара находится горячая жидкость с температурой снаружи — холодная с температурой . Значения коэффициентов теплоотдачи соответственно . Температуры поверхностей стенки неизвестны, обозначим их через (рис. 6-8).
При стационарном тепловом состоянии системы количество теплоты, переданное от горячей жидкости к холодной, можно выразить тремя уравнениями:
Из этих уравнений определяется значение :
Следовательно, коэффициент теплопередачи для шаровой стенки определяется оотношением
Обратная величина называется общим термическим сопротивлением теплопередачи шаровой стенки:
Рис. 6-8. Теплопередача через шаровую стенку.
При практических расчетах надо проверять соотношение термических сопротивлений; относительно малыми из них всегда можно пренебречь.
Читайте также:
