Стальной шарик массой 780 удерживается силой 28 с помощью стержня
Однородная балка массой m жёстко заделана в вертикальную стену. Длина балки L. Вес балки P. К концу балки закреплена нить, переброшенная через неподвижный блок. На нити закреплён груз весом P. Угол наклона нити к горизонту α. Определить реакции, возникающие в жёсткой заделке.
Будем решать это простейшую задачу строго следуя выше изложенной методике.
Поскольку условие нам понятно а эскиз уже готов, начнём с пункта 3 и приложим активные нагрузки. Они представлены двумя силами - сила тяжести балкиG и весом груза P. Ясно что вес груза натягивает нить, которая в свою очередь воздействует на балку силой T=P. Обозначим на рисунке активные силы зелёным цветом.
Поскольку в задаче требуется найти реакции в жёсткой заделке (точка А) будем рассматривать равновесие балки. В ведём систему координат XY.
Заменим действие жёсткой заделки на балку реакциями Rx, Ry и реактивный момент М.
Таким образом мы получаем плоскую произвольную систему сил, приложенных к выбранному нами объекту равновесия - балке.
Для такой системы сил можно составить три уравнения равновесия.
Сумма проекций всех сил на координатную ось Х:
Сумма проекций всех сил на координатную ось Y:
Сумма моментов относительно точки А. Эту точку выбираем для составления суммы моментов потому, что в ней пересекаются две неизвестные силы Rx и Ry:
Поскольку в полученной системе из трёх уравнений содержится четыре неизвестных записываем четвёртое уравнение, известное нам из курса физики (g - ускорение свободного падения):
Для нахождения неизвестных достаточно решить полученную систему уравнений, что с точки зрения алгебры не представляет никакой сложности.
21. Однородный стержень ОА упирается одним концом в угол и удерживается за другой конец нитью (рис.). Масса стержня m, а угол его наклона к горизонту равен α. Найти силу натяжения нити, а также силы, с которыми стержень давит на пол и на стену.
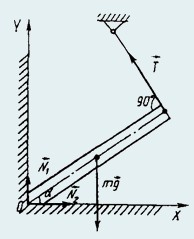
Решение.
На стержень действуют четыре силы: сила тяжести mg, сила натяжения нити Т, силы нормальных реакций пола N1 и стены N2.
Так как стержень находится в равновесии, то
mg + T + N1 + N2 = 0. (векторно)
Суммы проекций этих сил на оси ОХ и OY равны нулю:
N1 − mg + Tcosα = 0. (2)
Составим уравнение для моментов сил относительно оси, проходящей через точку А:
(1/2)mglcosα − Tl = 0,
где l − длина стержня.
Из этого уравнения найдем
T = (1/2)mgcosα.
Подставим это значение в уравнения (1) и (2):
N2 = mgsin2α, N1 = mg(1 + sin 2 α)/2.
Согласно третьему закону Ньютона, с такими по модулю силами давит стержень на стену и пол.
22. Однородный стержень АВ прикреплен к вертикальной стене посредством шарнира А и удерживается под углом α = 60° к вертикали с помощью невесомой веревки ВС, образующей с ним угол β = 30° (рис.). Определить силу натяжения веревки, а также модуль и направление силы реакции шарнира, если известно, что масса стержня m = 2,0 кг.
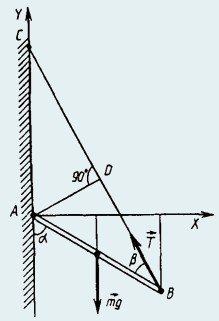
Решение.
На стержень действуют следующие силы: сила тяжести mg, приложенная к середине стержня и направленная вертикально вниз; сила натяжения веревки Т, приложенная в точке В и направленная вдоль веревки; сила реакции шарнира N. Модуль и направление силы N неизвестны, поэтому на рисунке она не показана.
Запишем условие равновесия в векторной форме:
mg + T + N = 0,
а затем в проекциях на оси ОХ и OY:
Nx − Tsin(α − β) = 0, (1)
Ny − mg + Tcos(α + β) = 0. (2)
(l/2)mgsinα − Tlsinβ = 0, (3)
где l − длина стержня.
Из уравнений (1) и (2) найдем:
Nx = Tsin(α − β), Ny = mg − Tcos(α − β).
Модуль силы N
Из уравнения (3) следует:
T = mgsinα/(2sinβ), T = 17 H.
Подставив полученное выражение Т в формулу (4), после преобразований и вычислений получим:
Направление вектора N определяется углом γ, который этот вектор составляет с осью ОХ. По значениям проекций Nx и Ny найдем
Т = mgsinα/(2sinβ),
получим после преобразований:
tgγ = (2sinβ − sinαcos(α − β))/(sinαsin(α − β)), tgγ = √3/3, γ = 30°.
23. Лестница опирается одним концом о вертикальную гладкую стену, а другим − о землю. Коэффициент трения лестницы о землю μ = 0,4. Центр тяжести лестницы находится на ее середине. Определить наименьший угол α, который лестница может образовать с горизонтом, не соскальзывая.
Решение.
На лестницу действуют сила тяжести mg, силы нормальных реакций N1 и N2 стены и земли, сила трения Fmp (рис.).
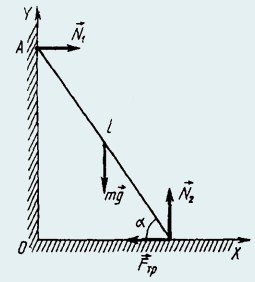
Лестница находится в равновесии, следовательно,
поэтому суммы проекций всех сил на оси ОХ и OY равны нулю:
Пусть l − длина лестницы. На основании равенства нулю суммы моментов всех сил относительно оси, проходящей через точку В, составим уравнение:
N1lsinα − mg(cosα)l/2 = 0.
Выразив из уравнения (2)
и подставив это значение в уравнение (1), найдем
Подставив это выражение в формулу (3), получим:
a = arctg(1/(2μ), α = 51°.
24. Четыре шара массами m1, m2, m3 и m4 надеты на стержень так, что их центры находятся на одинаковых расстояниях l друг от друга. Масса стержня m. Определить положение центра тяжести системы.
Решение.
Предположим, что центр тяжести находится на расстоянии х от центра левого шара (рис.).
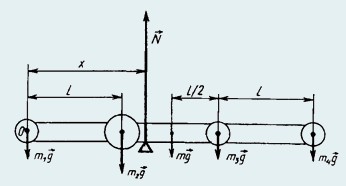
Если поставим в этом месте опору, то система будет находиться в равновесии. Следовательно, сумма моментов всех сил относительно оси, проходящей через любую точку, будет равна нулю. На систему действуют силы тяжести шаров m1g, m2g, m3g, m4g, стержня mg и сила нормальной реакции опоры N. Сумма моментов этих сил относительно оси, проходящей через точку О, равна нулю:
Сумма проекций всех сил на вертикальное направление также равна нулю:
Решив систему двух уравнений, найдем
25. Определить положение центра тяжести однородной круглой пластины радиуса R, в которой вырезано квадратное отверстие со стороной а = R/2 так, как показано на рисунке.
Решение.
Расположим пластину с отверстием так, чтобы ось симметрии была горизонтальна, и предположим, что вырезанный квадрат помещен на прежнее место.
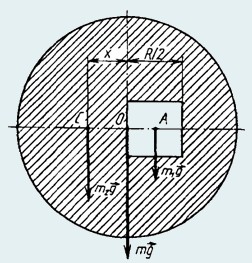
Тогда сила тяжести всего тела
где m1g − сила тяжести квадрата, приложенная в центре квадрата; m2g − сила тяжести пластинки с отверстием, приложенная в искомом центре тяжести С.
Относительно оси, проходящей через общий центр тяжести О, сумма моментов всех сил тяжести равна нулю:
где х − расстояние от точки О до точки С (центра тяжести пластинки с отверстием). Отсюда
Пусть h − толщина пластинки, ρ − плотность материала, из которого она изготовлена. Тогда:
m1 = ρ(R/2) 2 h = ρR 2 h/4,
m2 = m − m1 = ρπR 2 h − ρR 2 h/4 = (1/4)ρR 2 h(4π − 1).
26. Система, состоящая из неподвижного и подвижного блоков, находится в равновесии. К неподвижному блоку подвешен груз массой m1 = 20 кг. Найти
массу груза m2, силу натяжения нити и силу, действующую на ось неподвижного блока.
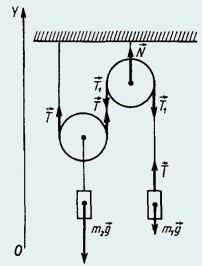
Решение.
При равновесии системы сумма проекций на ось OY сил, действующих на блоки и тела, равна нулю:
где T = Т1 − модуль силы натяжения нити; N − сила реакции оси неподвижного блока.
Согласно третьему закону Ньютона, на ось этого блока действует сила F = N. Тогда из уравнений (1) найдем:
T = 2•10 2 H, m2 = 40 кг, F = 4•10 2 H.
27. Две пружины, жесткости которых k1 = 400 Н/м и k2 = 600 Н/м, соединены последовательно (рис.). Какой должна быть жесткость пружины, которой можно было бы заменить эту систему из двух пружин?
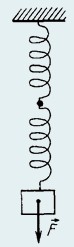
Решение.
При последовательном соединении пружин силы натяжения их одинаковы и равны по модулю приложенной силе F. По закону Гука
где k − жесткость системы (а значит, и жесткость пружины, которой можно было бы заменить эту систему); Δl − абсолютная деформация системы:
Δl1, Δl2 − деформация каждой пружины.
По закону Гука
Из выражений (1) − (3) находим:
Подставив эти значения в равенство (2), получим
31. Лестница длиной 4 м приставлена к идеально гладкой стене под углом 60° к горизонту. Коэффициент трения между лестницей и полом равен 0,4. На какую максимальную высоту над полом может подняться по лестнице человек, прежде чем она начнет скользить? Масса лестницы 5 кг, человека 60 кг.
Решение.
Когда человек поднимется на максимальную высоту, то должно выполняться равенство моментов сил тяжести человека, лестницы и реакции гладкой стенки относительно точки вращения B.
mgh/tgα + Mg(L/2)cosα = NALsinα, (1)
Так как лестница неподвижна, то выполняется равенство сил
NA = μ(mg + Mg). (2)
Подставим (2) в (1)
mgh/tgα + Mg(L/2)cosα = μ(mg + Mg)Lsinα.
h = μ(m + M)Lsinαtgα/m − MLsinα/(2m).
Подставим численные значения
h = (0,4•(60 + 5)•4•sin60•tg60)/60 − 5•4•sin60°/(2•60) = 2,5 (м)
1(Ш). На стержень действуют две параллельные силы, равные F1 = 10 H и F2 = 25 Н и направленные в противоположные стороны. Определите точку приложения и величину силы, уравновешивающей силы F1 и F2, если их точки приложения находятся на расстоянии l = 1,5 м друг от друга.
Решение:
Очевидно, что модуль уравновешивающей силы F равен разности модулей действующих на стержень сил:
Ясно также, что точка приложения уравновешивающей силы лежит на прямой, соединяющей точки приложения сил F1 и F, справа от большей силы. Обозначим искомое расстояние через x. Тогда по правилу моментов имеем:
Заметим, что в случае F1 = F2, т. е. когда на тело действует так называемая пара сил, уравновешивающей силы, в обычном смысле этого слава, нет. Под действием пары сил тело приходит во вращательное движение вокруг его центра тяжести.
Ответ: F = 15 H, x = 1 м.
2(Ш). К гвоздю, вбитому в стенку, привязана нить, намотанная на катушку. Катушка висит, касаясь стенки, как показано на рисунке. Радиус оси катушки r = 0,5 см, радиус ее щечек R = 10 см. Коэффициент трения между стенкой и катушкой μ = 0,1. При каком угле α между нитью и стенкой катушка висит неподвижно?
Решение:
Силы, действующие на катушку, изображены на рисунке.
Запишем условия равновесия катушки в виде:
N – Tsinα = 0
Учитывая, что Fmp = μN, получаем
sinα = r/(μR) = 1/2, и α = 30°.
Ответ: α = 30°.
4(Ш). Однородная тонкая пластинка имеет форму круга радиусом R, в котором вырезано круглое отверстие вдвое меньшего радиуса, касающегося края пластинки. Где находится ее центр тяжести?
Решение:
Из соображения симметрии ясно, что центр тяжести пластинки лежит на ее оси на некотором расстоянии x от центра круга. Если вложить обратно вырезанную часть пластинки, то центр тяжести пластинки сместится в ее центр. Запишем соответствующее правило моментов:
3x = R/2, и x = R/6.
Ответ: x = R/6.
5(Ш). На столе лежит однородный стержень массой 6 кг так, что две трети его длины находятся за краем стола. Какую силу необходимо приложить к концу стержня для удержания его в горизонтальном положении?
Решение:
На стержень действуют три силы: сила тяжести mg, удерживающая сила F и сила реакции опоры N, которая приложена в точке O, так как вначале вращения эта точка является опорой стержня.
Применим правило моментов относительно оси вращения в точке O:
где Mmg и MF – момент силы тяжести и приложенной силы F, а l3 и l1 – соответствующие плечи сил.
Момент силы N равен нулю, так как эта сила проходит через точку O, относительно которой рассматривается вращение, следовательно, плечо силы N равно нулю.
Из (1) находим, что
где l4 = l/2, получаем
l3 = 2l/3 – l/2 = l/6, F = mg/2.
Проводим расчет F = 6•10/2 = 30 H.
Ответ: F = 6•10/2 = 30 H.
(Ш). Куб опирается одним ребром на пол, другим – на гладкую вертикальную стенку. Определить, при каких значениях угла α возможно равновесие куба. Коэффициент трения куба о пол равен μ, ребро куба равно a.
Решение:
Уравнение проекций на вертикаль
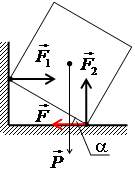
Уравнение проекций на горизонталь
F1 – реакция стенки.
Уравнение моментов относительно точки O
1 > tgα ≥ 1/(2μ + 1).
Если μ > 0, то α всегда меньше π/4, так как при α > π/4 куб опрокинется.
Ответ: 1 > tgα ≥ 1/(2μ + 1); если μ > 0, то α всегда меньше π/4, так как при α > π/4 куб опрокинется.
II) адиабатным расширением.
1. К покоящемуся на шероховатой горизонтальной поверхности телу приложена нарастающая с течением времени горизонтальная сила тяги F=b . t, где b – постоянная величина. На рисунке 1 представлен график зависимости ускорения тела от времени действия силы. Определите коэффициент трения скольжения.
2. Воду массой 500 г при температуре 95 0 С налили в теплоизолированный сосуд, где находился твердый нафталин при температуре 80 0 С. После установления теплового равновесия температура воды оказалась равна 80 0 С, при этом весь нафталин перешел в жидкое состояние. Пренебрегая потерями тепла, оцените, чему равна масса нафталина в сосуде.
3. Заряженная пылинка движется между двумя одинаковыми заряженными вертикальными пластинами, расположенными напротив друг друга. Разность потенциалов между пластинами 500 В, масса пылинки столь мала, что силой тяжести можно пренебречь. Какую кинетическую энергию приобретает пылинка при перемещении от одной пластины, если ее заряд 4 нКл? Ответ выразить в мкДж и округлить до целых.
4. Батарея дает максимальную силу тока Imах=5 А. Максимальное количество теплоты Q, которое может выделить эта батарея во внешней цепи за время t=10 с, равно 100 Дж. Найдите ЭДС батареи.
5. Какое количество теплоты подведено к двум молям одноатомного идеального газа при осуществлении процесса 1–2–3 (рис.2), если начальный объем его равен V1=1 л, а давление равно p1=100 кПа?
6. В магнитном поле с большой высоты падает с постоянной скоростью υ металлическое кольцо, имеющее диаметр d и сопротивление R. Плоскость кольца все время горизонтальна. Найдите массу кольца, если модуль индукции В магнитного поля изменяется с высотой Н по закону |В|=В0(1+αН). Сопротивлением воздуха пренебречь.
Вариант 2
1. Два поезда прошли одинаковый путь за одно и то же время. Однако один поезд, трогаясь с места, прошел весь путь равноускоренно с ускорением а=3 см/с 2 , а другой поезд половину пути шел со скоростью υ1=18 км/ч, а другую половину – со скоростью υ2=54 км/ч. Найдите пройденный путь.
2. Два шарика, массы которых m1=200 г и m2=300 г, подвешены на одинаковых нитях длиной L=50 см. Шарики соприкасаются. Первый шарик отклонили от положения равновесия на угол α=90° и отпустили. После абсолютно неупругого соударения шарики поднимутся на высоту, равную . см.
3. Удельная теплоемкость меди равна 380 Дж/(кг . К), а удельная теплоемкость воды 4200 Дж/(кг . К). Нагретый до температуры 70°С кусок меди массой 2 кг опускают в сосуд с водой, масса которой 4 кг. Начальная температура воды равна 20 0 С. Определите температуру, которая установится в сосуде (в 0 С), если известно, что потери тепла малы.
4. Один моль идеального одноатомного газа сначала охладили, а затем нагрели до первоначальной температуры 300 К, увеличив объем газа в 3 раза (см. рис.1). Какое количество теплоты отдал газ на участке 1–2?
5. На схеме, изображенной на рисунке 2, ЭДС источника ε=95 В, внутреннее сопротивление r=0,5 Ом. Сопротивления внешней цепи R1=R3=6 Ом, R2=R4=12 Ом. Показание амперметра равно … А.
6. Электрон влетает в область однородного магнитного поля с индукцией В=0,01 Тл со скоростью υ=1000 км/с перпендикулярно линиям магнитной индукции. Какой путь он пройдет к тому моменту, когда вектор скорости повернется на 1 градус?
Вариант 3
1. Автомобиль едет по горизонтальному участку дороги, затем въезжает на вогнутый мостик, имеющий форму дуги окружности. В нижней точке мостика автомобиль оказывает на него давление, в 3 раза большее, чем на горизонтальном участке дороги. Скорость автомобиля равна υ=72 км/ч. Радиус кривизны мостика равен …. м. Ответ округлить до целого.
2. Некоторое количество гелия расширяется: сначала – изобарно, затем – изотермически, совершая при этом работу А=3 Дж. Начальная и конечная абсолютные температуры отличаются в 2 раза. Начальные давление и объём: p1=1 кПа, V1=2л. Найти количество теплоты Q, полученное газом в этом процессе.
3. Ученик с помощью нагревательного элемента (спирали) нагревает парафин (рис.1) массой т=50 г, находящийся в сосуде при температуре плавления. Весь парафин расплавился за t=8 мин. Спираль и амперметр последовательно подсоединены к источнику постоянного тока с напряжением U=14 В. Показание амперметра равно I=2,5 А. Сопротивлением амперметра пренебречь. Удельная теплота плавления парафина r=147 кДж/кг. На нагревание парафина пошло …. % теплоты, выделившейся в спирали. Ответ округлите до целого.
4. Плоская горизонтальная фигура площадью 0,1 м 2 , ограниченная проводящим контуром с сопротивлением 5 Ом, находится в однородном магнитном поле. Пока проекция магнитной индукции на вертикаль ОZ медленно и равномерно убывает от некоторого начального значения B1z до конечного значения B2z= –0,1Тл, по контуру протекает заряд 0,008 Кл. Найдите B1z, если ось ОZ перпендикулярна плоскости фигуры.
5. В электрической цепи, показанной на рисунке 2, внутреннее сопротивление источника постоянного тока равно r=6 Ом, сопротивления резисторов R1=40 Ом, R2= 60 Ом. Через источник ЭДС течёт ток, сила которого равна I = 5 А. Величина ЭДС источника постоянного тока равна ε= . В.
6. Шар массой т=200 г, заряженный зарядом q=20 мкКл, висит на пружинке в однородном электрическом поле (рис.3). Жесткость пружины k=20 Н/м. Напряженность электрического поля Е=2 . 10 4 Н/Кл. Пружина находится в растянутом состоянии, при этом её деформация равна Δl=. см.
Вариант 4
1. Через какое время после выстрела стрела, пущенная вертикально вверх со скоростью 12 м/с, первый раз оказывается на высоте 4 м? Ответ округлить до десятых.
2. Воду массой 100 г при температуре 12 0 С поместили в калориметр, где находился лед при температуре –5 0 С. После установления теплового равновесия температура льда повысилась до 0 0 С, но масса льда не изменилась. Пренебрегая потерями тепла, оцените, какова была начальная масса льда в калориметре.
3. Пылинка массой 10 – 9 г несет на себе заряд 10 –8 Кл и движется вертикально между двумя одинаковыми горизонтальными пластинами, расположенными напротив друг друга, разность потенциалов между которыми 200 В. На сколько изменится кинетическая энергия пылинки при перемещении от одной пластины до другой на расстояние 1 см? Ответ выразить в мкДж и округлить до целых.
4. Стальной шарик массой m=780 г удерживается силой F=28 Н с помощью стержня, один конец которого на шарнире прикреплен к стене (см. рис.1). Длина стержня L=80 см, масса М=400 г. Затем шарик опускают в сосуд с водой. Как следует изменить точку приложения силы F, чтобы стержень при этом остался в горизонтальном положении?
5. Две параллельные шины, подключенные к аккумулятору с ЭДС ε0 и внутренним сопротивлением r, находятся в однородном магнитном поле с индукцией В. Шины замкнуты проводником длиной l и сопротивлением R, который перемещается по шинам без нарушения контакта перпендикулярно полю со скоростью υ. Пренебрегая сопротивлением шин, определите напряжение на зажимах источника, мощность тепловых потерь в проводнике, а также механическую мощность, подводимую к проводнику.
6. Над идеальным одноатомным газом в количестве вещества 1,4 моль совершили процесс 1–2–3–1 (рис.2). Какое количество теплоты подведено к системе на участке 1–2, если температура газа в точке 3 равна 580 К?
Вариант 5
1. Брусок массой М=1,8 кг и шарик массой т связаны между собой невесомой и нерастяжимой нитью, как показано на рисунке 1. Брусок находится на плоскости, составляющей угол α=45° с горизонталью. Коэффициент трения между поверхностью и телом равен μ=0,2. Чему равно максимальное значение массы т, при котором брусок с нулевой начальной скоростью начинает движение вниз?
2. По гладкой горизонтальной поверхности со скоростью υ1=1 м/с скользит шайба массой т1=90 г и налетает на неподвижную шайбу с массой m2=100 г. Рассчитайте энергию, которая перешла во внутреннюю при этом ударе, если после него первая шайба остановилась.
3. Аргон расширяется сначала адиабатно, потом изотермически, при этом конечная абсолютная температура в два раза ниже начальной. Совершенная газом за весь процесс работа А=5 Дж. Какое количество тепла было получено газом в процессе, если начальное давление и объем p1=1 кПа, V1= 4 л?
4. Полый пластмассовый шарик радиусом R=2 см имеет отверстие А диаметром d=1 мм (см. рис.2). Шарик постоянно равномерно заряжен отрицательным зарядом Q=–10 – 12 Кл. К шарику из точки, удаленной от него на расстояние r>>R, по прямой АО движется электрон с начальной скоростью υ0=10 6 м/с. Попав в отверстие, он ударяется о стенку шарика. Найдите кинетическую энергию электрона перед ударом.
5. Из проволоки, единица длины которой имеет сопротивление ρ, сделан плоский замкнутый контур, состоящий из двух квадратов площадью S1 и S2 (рис.3). Контур находится в однородном магнитном: поле с индукцией В0, направленной перпендикулярно плоскости контура. Какой заряд протечет через поперечное сечение провода при равномерном уменьшении индукции поля? Между пересекающимися на рисунке проводами контакта нет.
6. Два источника тока с одинаковой ЭДС и внутренними сопротивлениями r1=1 Ом, r2=2 Ом как при параллельном, так и при последовательном присоединении к одному и тому же внешнему сопротивлению показывают одну и ту же силу тока. Определите внешнее сопротивление.
Вариант 6
1. Кусок пластилина сталкивается со скользящим навстречу по горизонтальной поверхности стола бруском и прилипает к нему. Скорости пластилина и бруска перед ударом направлены противоположно и равны υпл=15 м/с и υбр=5 м/с. Масса бруска в 4 раза больше массы пластилина. Коэффициент трения скольжения между бруском и столом μ=0,17. На какое расстояние переместятся слипшиеся брусок с пластилином к моменту, когда их скорость уменьшится на 30%?
2. 10 моль одноатомного идеального газа сначала охладили, уменьшив давление в 3 раза, а затем нагрели до первоначальной температуры 300 К (рис.1). Какое количество тепла получил газ на участке 2–3?
3. К источнику тока с ЭДС ε=9 В и внутренним сопротивлением r=1 Ом подключили параллельно соединенные резистор с сопротивлением R=8 Ом и плоский конденсатор, расстояние между пластинами которого d=0,002 м (рис.2). Какова напряженность электрического поля между пластинами конденсатора?
4. Проводящий стержень длиной L=10 см и сопротивлением R=1 Ом может скользить по горизонтально расположенным параллельным шинам, которые соединены с источником постоянного тока с ε=10 В и внутренним сопротивлением r=1 Ом (рис.3). К середине стержня прикреплена невесомая пружина с коэффициентом жесткости k=0,1 Н/м, расположенная в горизонтальной плоскости. Перпендикулярно плоскости проводников действует однородное магнитное поле с индукцией В=10 –2 Тл. Пренебрегая сопротивлением шин и проводов, определите энергию деформации пружины.
5. Точка движется по оси х по закону х =5+ 4t–2t 2 (м). Координата, в которой скорость точки обращается в нуль, равна…(м).
6. Между двумя параллельными вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле напряженностью Е=10 5 В/м (рис.4). Между пластинами помещен шарик с зарядом q=100 пКл и массой m=30 мг на расстоянии d=0,5 см от левой пластины и на расстоянии b =2,5 см – от правой пластины. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени шарик ударится об одну из пластин? Пластины имеют достаточно большой размер. Учесть влияние гравитации.
Вариант 7
1. Идеальный газ при начальной температуре Т1=300 К занимает объем V1=20 л, находясь под давлением р1=0,3 МПа. Газ изохорно нагрели до Т2=420 К, а затем изобарно до Т3=510 К. Найдите работу газа (в кДж) при переходе из состояния 1 в состояние 3 (рис.1).
2. Два шарика висят, соприкасаясь, на нитях (рис.2). Правый шарик, масса которого m=0,2 кг, отклоняют на угол 90° и отпускают без начальной скорости. Какой должна быть масса левого шарика, чтобы в результате абсолютно неупругого удара половина кинетической энергии правого шарика перешла в тепло?
3. В вертикальном цилиндре с гладкими, тонкими, но прочными металлическими стенками под поршнем массой 10 кг заключён воздух (рис.3). Цилиндр закреплён на горизонтальной поверхности. Начальный объём воздуха под поршнем равен 4 л, площадь поперечного сечения цилиндра 100 см 2 , атмосферное давление принять равным 100 кПа. Поршень тянут пружиной жёсткостью 10 кН/м, медленно увеличивая её удлинение от нуля до 2 см. На какую величину при этом увеличится объём воздуха под поршнем?
4. Отрицательно заряженная диэлектрическая пластина, создающая однородное электрическое поле напряженностью Е=10 6 В/м, укреплена на горизонтальной плоскости. На нее с высоты h=10 см начинает падать шарик массой т=2 г, имеющий положительный заряд q=10 –8 Кл. Какой импульс передаст шарик пластине при абсолютно упругом ударе?
5. На схеме, изображенной на рисунке 4, ЭДС источника ε=95 В, внутреннее сопротивление r=0,5 Ом. Сопротивления внешней цепи R1=R3=6 Ом, R2=R4=12 Ом. Показание амперметра равно…А.
6. Протон и электрон, обладая одинаковыми импульсами, влетают в однородное магнитное поле перпендикулярно линиям индукции. Определите отношение радиусов траектории протона и электрона в этом магнитном поле.
Вариант 8
1. Невесомый стержень, находящийся в ящике с гладким дном и стенками, составляет угол 45° с вертикалью (рис.1). К середине стержня подвешен на нити шар массой 1 кг. Каков модуль горизонтальной составляющей силы упругости N, действующей на нижний конец стержня со стороны ящика?
2. Тело массой 800 г, нагретое до температуры 100°С, опустили в калориметр, содержащий 200 г воды. Начальная температура калориметра и воды равна 30°С. После установления теплового равновесия температура тела и воды в калориметре 37°С. Определите удельную теплоемкость вещества исследуемого тела. Теплоемкостью калориметра пренебречь. Ответ округлите до целых.
3. Пуля, летящая горизонтально со скоростью υ0=120 м/с, пробивает лежащую на горизонтальной поверхности стола коробку и продолжает движение в прежнем направлении, потеряв 80% скорости. Масса коробки в 16 раз больше массы пули. Коэффициент трения скольжения между коробкой и столом μ=0,5. На какое расстояние переместится коробка к моменту, когда ее скорость уменьшится вдвое?
4. Идеальный одноатомный газ в количестве 1 моль сначала изотермически расширился (T1=300 К). Затем газ изобарно нагрели, повысив температуру в 3 раза (рис.2). Какое количество теплоты получил газ на участке 2–3?
5. При подключении к источнику постоянного тока резистора сопротивлением R1=2 Ом в цепи идет ток I1=1,6 А. Если к источнику подключить резистор сопротивлением R2=1 Ом, то по цепи пойдет ток I2=2 А. Какое количество теплоты выделяется за 1 с внутри источника тока при подключении резистора R2?
6. Заряженная частица, движущаяся со скоростью 2 . 10 6 м/с, влетает в однородное магнитное поле с индукцией 0,52 Тл. Радиус дуги окружности, по которой движется частица в поле, равен 4 . 10 -2 м. Определите отношение заряда частицы к его массе. Полученный ответ умножьте на 10 -6 и округлите до целых.
Вариант 9
1. Движение материальной точки задано уравнением x=4 sin t (см), y=4cos t (см). Определите ускорение точки.
Лыжник массой 60 кг спустился с горы высотой 20 м. Какой была сила сопротивления его движению по горизонтальной лыжне после спуска, если он остановился, проехав 200 м? Считать, что по склону горы он скользил без трения.
3. Из начального состояния в конечное одноатомный идеальный газ можно перевести двумя способами:
I) сначала газ изохорически охлаждают до абсолютной температуры, которая в 32 раза меньше начальной, потом газ изобарно расширяется в восемь раз, в этом процессе газ совершает работу А=7 Дж;
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой - мы готовы помочь.


С 2.При выполнении трюка "Летающий велосипедист" гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты над краем трамплина (см. рисунок). На краю трамплина скорость направлена под некоторым углом к горизонту. Пролетев по воздуху, гонщик приземляется на горизонтальный стол на расстоянии S от точки старта, поднявшись в полёте на высоту h над столом. С какой высоты H начинал движение велосипедист?
С2. Два шарика, массы которых отличаются в 3 раза, висят, соприкасаясь, на вертикальных нитях (см. рисунок). Лёгкий шарик отклоняют на угол 90 ∘ и отпускают без начальной скорости. Каким будет отношение кинетических энергий тяжёлого и лёгкого шариков тотчас после их абсолютно упругого центрального удара?
С2. На доске, находящейся на гладкой горизонтальной поверхности стола, укреплена жёсткая изогнутая трубка (см. рисунок). В трубке на расстоянии H над столом удерживают шарик, который может скользить по трубке без трения. Масса шарика в 8 раз меньше массы доски с трубкой. Все тела покоятся. Шарик отпускают. В результате доска движется поступательно, не отрываясь от стола. Шарик вылетает из трубки со скоростью v. На каком расстоянии от стола находится левый горизонтальный конец трубки?
С2. Два шарика массой 50 и 100 г двигаются навстречу друг другу по одной прямой со скоростями 0,5 и 1 м/с соответственно. Определите скорости шариков после абсолютно упругого удара.
С2. Ареометр массой m представляет собой стеклянный сосуд, заполненный дробью, и цилиндрическую трубку с площадью поперечного сечения S. Он помещён в жидкость плотностью p. Ареометр погружают в жидкость несколько глубже, чем это нужно для его равновесия, и затем отпускают. Он начинает совершать колебания в вертикальной плоскости. Считая колебания гармоническими,определите период свободных колебаний ареометра.
С2. Стальной шарик массой m=780 г удерживается силой F=28 Н с помощью стержня, один конец которого на шарнире прикреплён к стене (см. рис.). Длина стержня L=80 см, масса M=400 г. Затем шарик опускают в сосуд с водой. Как следует изменить точку приложения силы F→, чтобы стержень при этом остался в горизонтальном положении?
С2. Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона к горизонту равен 30 ∘ . На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика в момент первого удара направлена вертикально вниз и равна 1 м/с.
С2. Сверхзвуковой самолёт летит горизонтально со скоростью v=1440 км/ч на высоте H=18000 м. Когда самолёт пролетает над зенитной установкой, из оружия производится выстрел. Какова должна быть минимальная начальная скорость снаряда и угол её с горизонтом, чтобы снаряд попал в самолёт?
С2. Пуля летит горизонтально со скорость 150 м/с., пробивает стоящий на горизонтальной поверхности льда брусок и продолжает движение в прежнем направлении со скоростью в 3 раза меньшей начальной. Масса бруска в 10 раз больше массы пули. Коэффициент трения скольжения между бруском и льдом равен 0,1. На какое расстояние сместится брусок к моменту, когда его скорость уменьшится на 10%?
С2. Брусок массой m1=500г. соскальзывает по наклонной плоскости с высоты 0,8м. и , двигаясь по горизонтальной поверхности, сталкивается с бруском массой m2=300г., движущимся ему на встречу со скоростью 2 м/с. Считая столкновение абсолютно неупругим, определите скорость брусков после столкновения. Трением при движении пренебречь.

Узнать стоимость написания работы -->
Вариант 3
3. Ученик с помощью нагревательного элемента (спирали) нагревает парафин (рис.1) массойт=50 г, находящийся в сосуде при температуре плавления. Весь парафин расплавился за t=8 мин. Спираль и амперметр последовательно подсоединены к источнику постоянного тока с напряжением U=14 В. Показание амперметра равно I=2,5 А. Сопротивлением амперметра пренебречь. Удельная теплота плавления парафина r=147 кДж/кг. На нагревание парафина пошло …. % теплоты, выделившейся в спирали. Ответ округлите до целого.
4. Плоская горизонтальная фигура площадью 0,1 м 2 , ограниченная проводящим контуром с сопротивлением 5 Ом, находится в однородном магнитном поле. Пока проекция магнитной индукции на вертикаль ОZ медленно и равномерно убывает от некоторого начального значения B1z до конечного значения B2z= –0,1Тл, по контуру протекает заряд 0,008 Кл. Найдите B1z, если ось ОZ перпендикулярна плоскости фигуры.
5. В электрической цепи, показанной на рисунке 2, внутреннее сопротивление источника постоянного тока равно r=6 Ом, сопротивления резисторов R1=40 Ом, R2= 60 Ом. Через источник ЭДС течёт ток, сила которого равна I = 5 А. Величина ЭДС источника постоянного тока равна ε= . В.
Вариант 4
34. Стальной шарик массой m=780 г удерживается силой F=28 Н с помощью стержня, один конец которого на шарнире прикреплен к стене (см. рис.1). Длина стержня L=80 см, масса М=400 г. Затем шарик опускают в сосуд с водой. Как следует изменить точку приложения силы F, чтобы стержень при этом остался в горизонтальном положении?
5 ε0 и внутренним сопротивлением r, находятся в однородном магнитном поле с индукцией В. Шины замкнуты проводником длиной l и сопротивлением R, который перемещается по шинам без нарушения контакта перпендикулярно полю со скоростью υ. Пренебрегая сопротивлением шин, определите напряжение на зажимах источника, мощность тепловых потерь в проводнике, а также механическую мощность, подводимую к проводнику.
Читайте также:
