Растяжение стального образца с измерением упругих деформаций
Цель работы: изучение методики испытаний на растяжение пластичных и хрупких материалов; определение характеристик прочности и пластичности углеродистой стали и серого чугуна при растяжении.
Механические испытания конструкционных материалов предназначены для экспериментального определения характеристик прочности, пластичность, упругости и многих других, которые необходимы для расчетов на прочность, жесткость и устойчивость элементов конструкций. Механические испытания проводятся также при контроле качества материалов на производстве, исследование влияния на механические свойства материалов химического состава и режимов термической обработки, низких и высоких температур, агрессивных сред, длительности нагружения, вида напряженного состояния и других факторов. Испытания материалов на растяжения являются основным и наиболее распространенным методом изучения механических свойств, поскольку они сравнительно просто осуществимы, подробно разработаны и нормированы (ГОСТ 1497-84), позволяют получать наиболее важные характеристики прочности, пластичности и упругости.
Постановка работы: На машине УГ-20 проведены испытания стального и чугунного образцов на растяжение Р, кН: (∆l+δ ), mm, где δ – упругие деформации нагруженных частей испытательной машины. Указанны масштабы нагрузок размеры образов до и после испытаний. Определить характеристики прочности и пластичности стали и чугуна при растяжении.
Испытание углеродистой стали на растяжение.
Пред испытанием измеряем диаметр d0=15,0 мм и длину l= 170 мм рабочей части образца. Вычисляем площадь сечения F0=πd0 2 /4 = 177 мм 2 = 177 10 -6 м 2 . Затем на рабочей длине наносим штангенциркулем риски, определяющие расчетную длину l0 =10d0=150 мм образца. Образец устанавливается в захваты испытательной машины и проводится его растяжение вплоть до разрушения. После разрушения определяем характерные размеры образца: диаметр шейки dш=9,40 мм; расчетная длина после разрыва l0p=180,6 мм. Вычисляем площадь сечения Fш = πdш 2 /4=69,4 мм 2 = 69,4 10 -6 м 2 .
Стальной образец при растяжении разрушается после образования шейки. В центре минимального сечения шейки зарождается трещина, которая затем развивается по конической поверхности примерно под углом 45 о , где действует τmax , до окончательного разрушения образца.
Записанную на машине УГ-20 кривую растяжения подвергаем обработке. Для этого проводим горизонтальную ось деформаций (∆l+δ ),соответствующую нулевой нагрузке. Затем из точки 0 пересечения прямолинейного участка кривой растяжения с осью (∆l+δ ), проводим вертикальную ось нагрузок Р. Зная масштабы записи нагрузок р=1,26 кН/мм и деформаций ∆l =0,48 кН/мм, наносим размерную сетку на диаграмму растяжения Р - (∆l+δ ). Из диаграммы растяжения видно, что если образец подвергнуть упругопластичному деформированию, а затем разгрузить, то линии разгрузки и повторного нагружения примерно параллельны прямолинейному участку диаграммы растяжения ( закон упругой разгрузки).
Определяем нагрузку Рпц, соответствующую пределу пропорциональности. Для этого в соответствии с ГОСТ 1497-84 на прямолинейном участке диаграммы Р - (∆l+δ ) проводим прямую МК, откладываем отрезок KN=0,5MK, проводим прямую 0N и параллельно ей – касательную к кривой растяжения. Ордината точки hпц представляет собой в масштабе нагрузку Рпц=hпцμp= 47,5 мм 1,26 кН/мм = 59,85кН.
Нагрузка Ру, соответствующая пределу упругости, определяется по допуску относительной остаточной деформации 0,05%. Это соответствует абсолютной остаточной деформации ∆l0,05=0,0005l = 0,0005 170= 0,085 мм. На оси деформации в масштабе откладываем∆l0,05,проводим прямую, параллельную линейному участку. Ордината hy точки пересечения прямой с кривой растяжения соответствует в масштабе нагрузок Ру=hуμp=52,5 1,26 = 66,15 кН.
Нагрузка РТ соответствующая физическому пределу текучести, определялся ординатой hT площадки текучести на диаграмме растяжения Рт=hтμp=57,5 1,26 = 72,45 кН.
Нагрузка Рв, соответствующая пределу прочности, - это наибольшая нагрузка при разрыве образца: Рв=hвμp=95 1,26= 119,7 кН.
Нагрузка Рк, соответствующая разрушению образца, равна: Рк=hкμp=89,0 1,26=112,14 кН.
Наносим на диаграмму Р - (∆l+δ ) полученные нагрузки.
Определяем характеристики прочности стали при растяжении:
- предел пропорциональности (напряжение, превышение которого ведет к нарушению линейной зависимости между нагрузкой Р и удлинением ∆l образца)
- предел упругости (напряжение, которое соответствует относительной остаточной деформации 0,05%)
- физический предел текучести( напряжение, которое соответствует площадке текучести на диаграмме растяжения)
- предел прочности или временное сопротивление (напряжение, которое соответствует наибольшей нагрузке после разрушения образца)
- сопротивление отрыву в шейке образца
Чем выше эти характеристики, тем материал прочнее.
Находим характеристики пластичности при растяжении:
- относительное остаточное удлинение после разрыва образца
- относительное остаточное сужение в шейке после разрыва образца
Чем выше характеристикиИспытание серого чугуна на растяжение
Чугунный образец до испытаний аналогичен стальному( d0=15,0 мм; F0=πd0 2 /4 = 177 мм 2 = 177 10 -6 м 2 ; l0 =10d0=150 мм). Вид образца и его характерные размеры после разрыва:
Fр=πd0р 2 /4 = 174 мм 2 = 174 10 -6 м 2
Чугунный образец при растяжении разрушается по ослабленному пороками структуры сечению перпендикулярно оси путем отрыва.
Обработка диаграммы растяжения чугунного образца проводится аналогично рассмотренной для стального образца.
По диаграмме Р - (∆l+δ )определяем нагрузку, соответствующую пределу прочности: Рвр=hврμp=68 0,360 = 24,5 кН
Диаграмма растяжения стали
Ее построение является промежуточным этапом в процессе определения механических характеристик материалов (в основном стали и других металлов).
Диаграмму растяжения материалов получают экспериментально, при испытаниях образцов на растяжение.
Для этого стальные образцы стандартных размеров закрепляют в специальных испытательных машинах (например УММ-20 или МИ-40КУ) и растягивают до полного разрушения (разрыва). При этом специальные приборы фиксируют зависимость абсолютного удлинения образца от прикладываемой к нему продольной растягивающей нагрузки и самописец вычерчивает кривую характерную для данного материала.
На рис. 1 показана диаграмма растяжения малоуглеродистой стали. Она построена в системе координат F-Δl , где:
F — продольная растягивающая сила, [Н];
Δl — абсолютное удлинение рабочей части образца, [мм]

Как видно из рисунка, диаграмма имеет четыре характерных участка:
I — участок пропорциональности;
II — участок текучести;
III — участок самоупрочнения;
IV — участок разрушения.
Построение диаграммы
Рассмотрим подробнее процесс построения диаграммы.
В самом начале испытания на растяжение, растягивающая сила F , а следовательно, и деформация Δl стержня равны нулю, поэтому диаграмма начинается из точки пересечения соответствующих осей (точка О ).
На участке I до точки A диаграмма вычерчивается в виде прямой линии. Это говорит о том, что на данном отрезке диаграммы, деформации стержня Δl растут пропорционально увеличивающейся нагрузке F.
После прохождения точки А диаграмма резко меняет свое направление и на участке II начинающемся в точке B линия какое-то время идет практически параллельно оси Δl , то есть деформации стержня увеличиваются при практически одном и том же значении нагрузки.
В этот момент в металле образца начинают происходить необратимые изменения. Перестраивается кристаллическая решетка металла. При этом наблюдается эффект его самоупрочнения.
После повышения прочности материала образца, диаграмма снова «идет вверх» (участок III ) и в точке D растягивающее усилие достигает максимального значения. В этот момент в рабочей части испытуемого образца появляется локальное утоньшение (рис. 2), так называемая «шейка», вызванное нарушениями структуры материала (образованием пустот, микротрещин и т.д.).

Рис. 2 Стальной образец с «шейкой»
Вследствие утоньшения, и следовательно, уменьшения площади поперечного сечения образца, растягиваещее усилие необходимое для его растяжения уменьшается, и кривая диаграммы «идет вниз».
В точке E происходит разрыв образца. Разрывается образец конечно же в сечении, где была образована «шейка»
Работа затраченная на разрыв образца W равна площади фигуры образованной диаграммой. Ее приближенно можно вычислить по формуле:
По диаграмме также можно определить величину упругих и остаточных деформаций в любой момент процесса испытания.
Для получения непосредственно механических характеристик металла образца диаграмму растяжения необходимо преобразовать в диаграмму напряжений.
Испытание на растяжение стали
Лабораторная работа №1 по испытанию на растяжение и разрыв стального образца из малоуглеродистой стали (видео).
Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.
Основные сведения
Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.
Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).
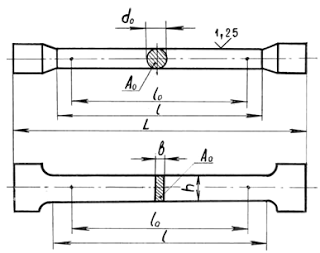
Рис. 1.1. Образцы для испытания на растяжение
Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:
В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.
В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).
Порядок выполнения и обработка результатов
Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.
Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).
В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.
На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.
Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».
На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.
При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.
Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.
Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.
Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δ l/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.
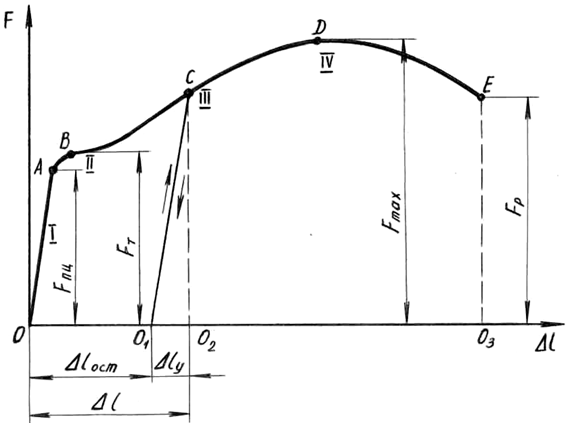
Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали
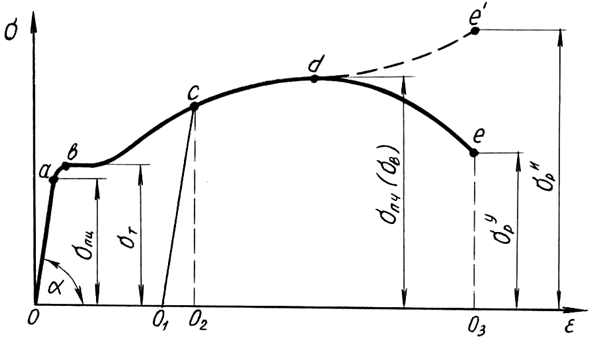
Рис. 1.3. Условная диаграмма напряжений при растяжении
Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):
σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;
σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;
σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.
Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);
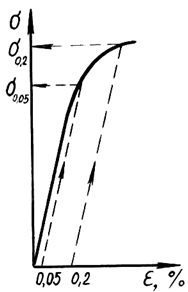
Рис. 1.4. Определение предела упругости и условного предела текучести
σпч ( σв ) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;
σр – напряжение разрыва. Определяется условное σ у р и истинное σ и р=Fр/Аш , где Аш – площадь сечения «шейки» в месте разрыва.
Определяются также характеристики пластичности – относительное остаточное удлинение
где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение
По диаграмме напряжений можно приближенно определить модуль упругости I рода
причем после операции наклепа σпц возрастает на 20-30%.
Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.
Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.
По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали
Контрольные вопросы
- Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточныеабсолютные деформации при нагружении силой, большей, чем Fт.
- На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
- Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
- Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
- Дайте определение предела пропорциональности.
- Дайте определение предела упругости.
- Дайте определение предела текучести.
- Дайте определение предела прочности.
- Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
- Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
- Как определяется остаточная деформация после разрушения образца?
- Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
- Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
- Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
- Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
- Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
- Можно ли определить модуль упругости материала по диаграмме напряжений?
- Как определить работу, затрачиваемую на деформации текучести лабораторного образца?
Методические указания к лабораторной работе «испытание материалов. Растяжение стального образца с измерением упругих деформаций»
Кутрунова, З. С. Техническая механика: методические указания к лабораторной работе «Испытание материалов. Растяжение стального образца с измерением упругих деформаций» для студентов направления 280700.62 «Строительство» всех форм обучения / З. С. Кутрунова. – Тюмень: РИО ФГБОУ ВПО «ТюмГАСУ», 2014. – 18 с.
Методические указания к лабораторной работе составлены на основании требований Федерального Государственного образовательного стандарта по направлению «Строительство» и способствуют развитию умений использовать современные программы, методики, приборы и оборудование.
Процесс выполнения лабораторной работы « Испытание на сжатие деревянных образцов » способствует развитию у студентов профессиональных компетенций:
ПК-2 – способность выявлять естественнонаучную сущность проблем, возникающих в ходе профессиональной деятельности, привлечение для их решения соответствующего физико-математического аппарата;
ПК-5 – владение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией.
Рецензент: Соколов В. Г.
© ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет»
© Кутрунова З. С.
Редакционно-издательский отдел ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет»
3 Испытательная машина и измерительные инструменты………………………..6
5 Подготовка и проведение испытания…………………………………………. 9
6 Анализ диаграммы растяжения………………………………………………. 10
6.1 Характеристики прочности материала…………………………………10
6.2 Характеристики пластичности материала……………………………..14
6.3 Характеристики статической вязкости материала……………………14
Библиографический список………. ……………………………………………. 18
Цели опыта – ознакомление c принципами работы разрывной испытательной машины INSTRON и экстензометра INSTRON. Проверка закона Гука при растяжении, определение модуля упругости стали и её механических характеристик.
Для проверки закона Гука и определения модуля упругости материала необходимо измерение упругих деформаций при растяжении его в пределах пропорциональности.
С другой стороны, для определения механических характеристик и, в частности, относительных остаточных деформаций, являющихся мерой пластичности материала, необходимо довести образец до разрыва.
2 ОПИСАНИЕ РАБОТЫ
Испытание на растяжение является наиболее распространенным видом исследования материалов, так как при нем наиболее ярко выявляются характеристики прочности и пластичности материалов.
ГОСТ 1497-84 «Металлы. Методы испытаний на растяжение» устанавливает методы статических испытаний на растяжение черных и цветных металлов и изделий из них для определения следующих механических характеристик материалов:
Для большинства материалов в пределах упругого деформирования до предела пропорциональности между напряжениями и деформациями имеет место прямо пропорциональная зависимость, которая была установлена Робертом Гуком. 1
В условиях осевого растяжения, когда только по двум граням выделенного из объёма материала элемента действуют нормальные напряжения (рисунок 1),
Рисунок 1
наблюдается его линейное деформирование - продольное удлинение и изменение размеров его поперечного сечения. При этом нормальное напряжение прямо пропорционально относительной продольной деформации:
(1)
Данная зависимость получила название закона Гука при растяжении-сжатии. Коэффициент называется модулем упругости или модулем Юнга. 2 Модуль упругости характеризует жесткость материала и имеет размерность напряжения - паскаль( Па).
Образец изготовлен в соответствии с ГОСТ 1497-84 «Металлы. Метод испытаний на растяжение» на металлорежущем станке, сохранены поверхностные слои проката. Длина рабочей части образца диаметр .
При изготовлении образцов должны быть выполнены следующие требования: высокая однородность сечения образца по его длине, соосность и высокое качество поверхности (малая шероховатость, отсутствие царапин и надрезов).
3 ИСПЫТАТЕЛЬНАЯ МАШИНА И ИЗМЕРИТЕЛЬНЫЕ ИНСТРУМЕНТЫ
В работе используется испытательная разрывная машина корпорации INSTRON, которая является мировым лидером в области производства оборудования для испытаний материалов.
История INSTRON началась в 1947 году, когда два инженера из Массачусетского технологического университета Джордж Бурр и Гарольд Хиндманн разработали и собрали первую электромеханическую разрывную машину для определения механических свойств материалов, которые использовались для изготовления парашютов. Машина была создана на основании имеющихся достижений техники и электроники того времени. Разрывная машина оказалась настолько удачной, что несколько других институтов заказали несколько новых аналогичных систем. Так начал свою деятельность INSTRON. С тех пор два человека тянущие в разные стороны парашютную стропу стали эмблемой INSTRON (рисунок 3)
Рисунок 3
Сегодня корпорация INSTRON Ltd является крупнейшим производителем испытательного оборудования в мире. За последние десятилетия в состав корпорации вошли признанные лидеры в области создания испытательного и измерительного оборудования: 1989 год - SFL, Торнбери, Англия (ведущий производитель температурных камер, печей и систем управления температурными испытаниями); 1993 год- Wilson Instruments (ведущий производитель твердомеров в Северной Америке, лидер в производстве оборудования для определения твердости по Роквеллу); 1993 год - WOLPERT (признанный лидер в производстве твердомеров в Европе); 1995 год- SHORE Instruments Co (изобретатели и лидеры в производстве твердомеров для резины); 1995 год - Wilson Instruments (ведущий производитель твердомеров в Северной Америке, лидер в производстве оборудования для определения твердости по Роквеллу); 1995 год – CARL SCHENK AG (признанный лидер в производстве серво-гидравлических машин для усталостных и структурных испытаний); 1998 год - SATEC (старейший производитель превосходных гидравлических систем для испытаний материалов).
Испытательные машины фирмы INSTRON отличаются высокой степенью надёжности, точностью задания и измерения нагрузок, перемещений и деформаций.
В лаборатории сопротивления материалов Тюменского государственного архитектурно-строительного университета установлена испытательная установка Instron 3382 (рисунок 4).
Рисунок 4
Эта напольная электромеханическая разрывная машина отвечает всем требованиям европейских и американских стандартов, а также внесена в Государственный реестр средств измерений Российской Федерации.
Технические характеристики электромеханической машины Instron 3382: максимальная нагрузка 100 кН, погрешности измерения нагрузки и деформации +/-0,5% от измеряемой величины.
Машина имеет современный аппарат для регистрации результатов испытаний, результаты опыта выводятся на монитор компьютера и хранятся в отдельном файле, что позволяет быстро обрабатывать данные, создавать и хранить отчеты по испытаниям, а также выводить их на печать. Диаграммный аппарат автоматически записывает кривую «нагрузка-деформация», рисунок 6.
4 ЭКСТЕНЗОМЕТР
Измерение деформаций поверхностного слоя образца под действием заданных внешних сил называется тензометрированием. Тензометрия (от лат. tensus – напряженный, натянутый и греч. metreo - измеряю) – экспериментальное определение напряженного состояния конструкций, основанное на измерении малых деформаций. Измерение деформаций с помощью тензорезистивных преобразователей (тензометров) – одно из самых сложных в технике электрических измерений. Сложность определяется малым диапазоном изменения сопротивления под воздействием деформации.
В данной лабораторной работе используется современный навесной экстензометр INSTRON с базовой длиной 50мм и перемещением +50% 5%, рисунок 5.. Основными элементами экстензометра являются тензодатчики (тензорезисторы) и непосредственно электронный измеритель деформаций -преобразователь. Расстояние между тензодатчиками называется базовой длиной.
Рисунок 5
Экстензометры предназначены для точного измерения относительного удлинения (или продольной деформации) непосредственно на образце и определения таких параметров как модуль упругости, физический предел текучести, условный предел текучести, технический предел прочности. Использование экстензометров позволяет исключить упругую деформацию нагружающей рамы, захватов и концевых участков образцов.
5 ПОДГОТОВКА И ПРОВЕДЕНИЕ ИСПЫТАНИЯ
Перед установкой образца в испытательную машину производиться измерение поперечных размеров образца и длины его рабочей части. Размеры поперечного сечения образца измеряют с погрешностью до 0,01 мм, рабочую длину образца c погрешностью до 0,1мм. Нарисовать эскиз стержня в таблице 1.
Измерение поперечных размеров образца проводят в трех местах: в средней части и на границах рабочей длины образца. По наименьшему из полученных результатов измерений определяют начальную площадь в его рабочей части с отклонением не более 0,01 мм. Результаты измерений и результаты расчетов занести в таблицу 2.
Далее необходимо проверить готовность к испытанию разрывной машины и диаграммного аппарата. Затем установить образец в захваты испытательной машины.
Включить нагружающее устройство испытательной машины.
Откалибровать тензометр и прикрепить на образец.
Запустить программу эксперимента.
Экстензометр снимают после прохождения предела пропорциональности, .
По стандарту на проведение испытаний ГОСТ 1497-84, металлы, при испытании скорость перемещения подвижного захвата машины не должна превышать до предела текучести -2 мм/мин, за пределом текучести – 10 мм/мин.
В процессе испытания наблюдать за поведением образца, автозаписью диаграммы растяжения на мониторе компьютера.
После разрушения образца выключить испытательную машину, извлечь из захватов обе половины образца и снять диаграмму растяжения.
Произвести обмер разрушенного образца. Для этого нужно плотно сложить обе части образца так, чтобы их оси образовали прямую линию, и измерить штангенциркулем длину расчетной части образца после разрыва , а также минимальные размеры образца в месте разрыва (в шейке).
Определить площадь поперечного сечения в «шейке».
Результаты испытаний записать в соответствующие графы отчета (таблицы 1, 2, 3).
Результатом эксперимента является истинная диаграмма растяжения 3 :
Рисунок 6
По диаграмме растяжения, длине и поперечных размеров сечения образца до и после испытания определяются следующие характеристики механических свойств, свидетельствующие о прочности и пластичности исследуемого материала.
Прямолинейный участок в начале диаграммы (рисунок 6) характеризует прямую пропорциональность между нагрузкой и деформацией. Точка соответствует напряжению предела пропорциональности .
Предел пропорциональности - наибольшее напряжение, до которого справедлив закон Гука, (МПа):
Для определения по диаграмме растяжения (рисунок 6) необходимо провести прямую , совпадающую с участком диаграммы, (рисунок 7).
Рисунок 7
Ордината точки , в которой кривая растяжения отклоняется от прямой , определяет нагрузку на пределе пропорциональности . Зона называется зоной упругости, здесь возникают только упругие деформации.
Данные, характеризующие эту зону, позволяют определить значение модуля упругости .
Способность материала сопротивляться деформированию в упругой области определяется модулем упругости , который пропорционален тангенсу угла наклона линейного участка диаграммы,
В непосредственной близости от точки , находится точка , соответствующая пределу упругости .
Предел упругости - максимальное напряжение, при котором в материале не обнаруживается признаков пластической (остаточной) деформации. Предел упругости существует независимо от закона прямой пропорциональности. Он характеризует начало перехода от упругой деформации к пластической деформации. У большинства металлов значения предела пропорциональности и предела упругости незначительно отличаются друг от друга. В нашем случае не требуется высокой точности вычислений, поэтому предел упругости принимается равным пределу пропорциональности.
При дальнейшем нагружении деформация растёт быстрее нагрузки и на диаграмме появляется криволинейный участок. Затем криволинейная часть диаграммы переходит почти в горизонтальный участок – площадку текучести. Здесь деформации растут практически без увеличения нагрузки – материал «течёт». Зона ВС называется зоной текучести.
Точка соответствует физическому пределу текучести . Нагрузку при физическом пределе текучести, если последний выражен площадкой, определяют непосредственно по диаграмме (рисунок 6). Предел текучести физический (МПа)- напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки:
(3)
Для металлов, у которых диаграмма растяжения не имеет площадки текучести, по этой диаграмме определяют условный предел текучести. Это напряжение при остаточном удлинении, равном 0,2% от длины образца, определяемое по формуле
(4)
Значение нагрузки определяют графически из диаграммы растяжения. Для чего по оси удлинений диаграммы в масштабе от точки откладывают отрезок (рисунок 8). Из точки проводят прямую , параллельную прямой до пересечения с кривой диаграммы растяжения в точке .
За площадкой текучести диаграмма опять идёт вверх по кривой. Образец приобретает способность сопротивляться нагрузкам до значения . На кривой растяжения точка D соответствует величине наибольшей нагрузки , предшествующей разрушению образца. По значению определяют основной показатель прочности материала – временное сопротивление.
Рисунок 8
Временное сопротивление представляет собой наибольшее напряжение, которое выдерживает материал перед разрушением (МПа):
(5)
До точки D удлинение образца происходит по всей длине, первоначальная цилиндрическая форма образца сохраняется, а поперечные сечения изменяются незначительно и также равномерно.
При достижении максимальной нагрузки на образце в наиболее слабом месте возникает локальное уменьшение поперечного сечения - «шейка» (рисунок 9).
Рисунок 9
Дальнейшее растяжение происходит в зоне «шейки», после чего наступает разрушение образца. Точка соответствует истинному пределу прочности :
где - площадь поперечного сечения образца в месте разрыва (шейки), .
Полная деформация образца складывается из остаточной деформации ( на рисунке 6), не исчезающей после разрушения и упругой деформации (отрезок ), исчезающей после разрушения образца:
Относительное удлинение - отношение абсолютного удлинения к первоначальной длине, выраженное в процентах:
(8)
Относительное сужение - отношение уменьшения площади поперечного сечения образца после разрушения к первоначальной площади поперечного сечения, выраженное в процентах:
(9)
Характеристики статической вязкости материала
Помимо найденных выше величин и деформаций, характеризующих пластичность и прочность материала, для оценки качества испытанной стали важно определить также количество работы, затраченной на разрыв образца. Чем больше работы необходимо затратить для разрыва образца, тем больше энергии в состоянии поглотить материал не разрушаясь, тем лучше он будет сопротивляться ударным нагрузкам, поглощая кинетическую энергию удара.
Величина полной работы, затраченной при растяжении образца до его разрыва, графически изображается площадью диаграммы растяжения и вычисляется по формуле:
(10)
Чтобы получить величину, характеризующую не сопротивление образца, а сопротивление материала, необходимо подсчитать удельную работу растяжения, то есть количество работы, приходящееся на единицу объёма испытанного образца:
Удельная работа характеризует способность материала поглощать энергию при разрыве, вязкость материала и сопротивляемость его динамическому воздействию нагрузки.
Используя формулы (1-11), заполнить таблицу №3 и построить условную диаграмму растяжения образца (по вертикальной оси откладываются нормальные напряжения, а по горизонтальной оси – относительные деформации).
Испытание проводится на машине……………………………………….
Диаграмма деформирования строится автоматически.
Таблица 1 - Эскизы образцов до и после испытания.
лаб_р
Цель работы: экспериментальная проверка закона Гука при растяжении. Определение модуля Юнга и коэффициента Пуассона стали.
В работе подвергается испытанию на растяжение плоский стальной образец в пределах упругих деформаций. На образце (рис. 1) установлены два продольных и два поперечных тензометра.
Для измерения деформаций образца в работе используется электротензометрический метод, изложенный в лабораторной работе № 3.
Проверка закона Гука
Опытная проверка закона Гука при растяжении производится на основе экспериментально определенной диаграммы растяжения (рис.2), которая
строится по результатам испытаний.
P 0 ∆ P ∆ P ∆ P ∆ P ∆ P
∆ n 1 ∆ n 1 ∆ n 1 ∆ n 1 ∆ n 1
Справедливость закона Гука устанавливается наличием на диаграмме прямолинейного участка.
Определение модуля Юнга материала
Модуль Юнга материала определяется по формуле закона Гука:
где Р – ступень нагрузки;
l – база тензометра продольной деформации; А – площадь поперечного сечения образца;
l – абсолютное удлинение образца на отрезке длиной l .
Зная среднее приращение отсчетов n 1cp электротензометра продольной деформации (из таблицы наблюдений) и цену деления прибора в относительной
деформации на одно деление K ε , можно вычислить относительную продольную деформацию образца:
Цена деления прибора – электротензометра устанавливается опытным
путем (см. работу № 3).
Подставляя в формулу (1)
данные опыта (2), получим:
Определение коэффициента Пуассона
Коэффициентом Пуассона или коэффициентом поперечной деформации называется отношение относительной поперечной деформации к относительной продольной деформации, взятое по модулю:
где μ – коэффициент Пуассона;
ε – относительная продольная деформация;
ε′ – относительная поперечная деформация.
Относительная поперечная деформация образца вычисляется по формуле:
где – среднее приращение отсчетов электротензометра поперечной деформации (берется из таблицы наблюдений);
K ε′ – цена деления электротензометра поперечной деформации.
Если характеристики (база, цена деления) тензометров продольной и поперечной деформации одинаковы, то величина коэффициента Пуассона определяется по формуле:
Испытательная машина ГЗИП
Работа выполняется на испытательной машине ГЗИП (рис. 3), предельная нагружающая способность которой может быть 2 т (20 кН) и 5 т (50 кН). Образец 1 закрепляют в захваты 2 и 3. Нижний захват перемещается с помощью винта 4. Перемещение винта осуществляется рукояткой 5. Нагрузка измеряется силоизмерителем 6.
Порядок выполнения работы
1. Замерить размеры поперечного сечения образца b и h .
2. Установить образец в захваты машины.
3. Нагрузить образец начальной нагрузкой P 0 (для обжатия образца в захватах машины).
4. Произвести начальные отсчеты по продольным и поперечным тензометрам.
5. Плавно увеличивать нагрузку одинаковыми ступенями до напряжения в образце, равного (0,80 ÷ 0,90) σ пц . Одновременно на каждой стадии нагружения делать отсчеты по тензометрам.
6. По окончании опыта разгрузить образец до нагрузки P 0 и снять
контрольные отсчеты по тензометрам, которые должны совпадать
7. Выполнить отчет по прилагаемой форме.
ЛАБОРАТОРНАЯ РАБОТА № 4
Растяжение стального образца с измерением упругих деформаций
Цена деления электротензометра K ε = ………….
Схема образца с тензометром
Размеры поперечного сечения
Отсчеты в делениях прибора
ЛАБОРАТОРНАЯ РАБОТА № 5 Испытание стального круглого образца на кручение
1) проверка закона Гука при кручении;
2) определение модуля упругости при сдвиге стали;
3) определение условного предела прочности при кручении стального образца.
Угол закручивания стержней круглого поперечного сечения в пределах упругих деформаций связан с крутящим моментом линейной зависимостью в соответствии с законом Гука:
где М к – величина крутящего момента;
l – расстояние между сечениями, на базе которого измеряется взаимный угол закручивания;
I ρ – полярный момент инерции поперечного сечения;
G – модуль поперечной упругости материала образца.
Принимаемые в процессе эксперимента величины крутящего момента М к и установленные значения соответствующих углов закручивания φ к при известных значениях базовой длины l и полярного момента инерции поперечного сечения I ρ позволяют определить величину модуля поперечной упругости материала :
где М к – приращение крутящего момента на одну ступень нагружения;
Δφ ср – среднеарифметическое значение угла закручивания на одну ступень нагружения.
Читайте также:
