Расчет прочности сжатых стальных элементов
Элементы металлических конструкций в процессе эксплуатации подвергаются действию растяжения, сжатия, изгиба, кручении и различных комбинаций этих воздействий. Рассмотрим методы расчета на прочность элементов металлических конструкций т.е. методы расчета по первому предельному состоянию.
Центрально-сжатые и центрально - растянутые элементы. Ранее для вычисления напряжений в этом случае была выведена формула ( 3.1 ). Эту формулу легко превратить в соотношение для проверки прочности.
где Аn - площадь поперечного сечения элемента за вычетом ослаблений; N - усилие от действия расчетных нагрузок; γc - коэффициент условий работы; R - расчетное сопротивление. Если расчет ведется по упругой стадии, R = Ry. Если расчет ведется для условий, когда возможна эксплуатация конструкции и после достижения материалом напряжений текучести, в качестве расчетного сопротивления выбирается максимальное значение из величин Ry и Ru / γu . Здесь Ry и R u - расчетные сопротивления материала, соотвественно, по пределу текучести и по временному сопротивлению;
γu = 1,3 - коэффициент надежности по материалу при расчете конструкций по временному сопротивлению.
Относительно разницы между растяжением и сжатием. Формула (4.1) для растяжения абсолютно корректна. Что же касается сжатия, то это соотношение справедливо только для коротких стержней. Известно, что стержни при сжатии, до исчерпания прочности самого сечения, могут потерять устойчивость, см. рис.4.1. Следует заметить, что хотя это напряженное состояние называется «центральным сжатием» на практике оно никогда не реализуется. Происходит это по многим причинам. Во-первых, нагрузка никогда не может быть приложена точно в центре сечения, так как все конструктивные элементы выполняются с допусками. Во-вторых, материал в сечении и по длине стержня всегда неоднороден. Эти и другие причины приводят к тому, что сжимающая сила оказывается всегда приложенной с некоторым эксцентриситетом к центру тяжести поперечного сечения и этот эксцентриситет создает дополнительный изгибающий момент, приводящий в итоге к потере устойчивости.
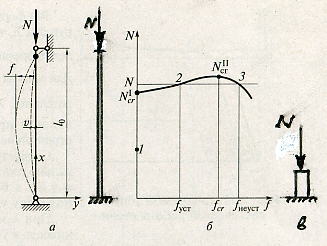
Рис. 4.1. Работа центрально сжатого стержня:
а - стержень и его расчетная схема, б – зависимость между нагрузкой и прогибом стержня,
в - сжатие короткого стержня.
Такое напряженное состояние стержня при действии сжимающей силы называется продольным изгибом. Поэтому формула проверки прочности стержня при сжатии будет
выглядеть так: σ = N / ( φ A ) ≤ Ry γc , ( 4.2 )
где: φ - коэффициент продольного изгиба; A – площадь поперечного сечения стержня. Коэффициент φ всегда меньше 1 и зависит от гибкости стержня λ. Гибкость стержня зависит от способа его закрепления по концам и от геометрических характеристик сечения: λ =где - расчетная длина стержня; μ - коэффициент расчетной длины;
i =При действии изгиба производится проверка по нормальным и касательным напряжениям. При расчете по упругой стадии проверка нормальных напряжений производится по соотношению преобразованному из соотношения ( 3.2 ):
где M - расчетный изгибающий момент; Wn,min - момент сопротивления сечения
с учетом ослаблений; σmax - напряжение в крайних волокнах поперечного сечения.
Касательные напряжения проверяются на основании формулы Н.Г. Журавского:
τ = Q S / ( J t ) ≤ Rs γc , ( 4.5 )
где Q - поперечная сила от действия расчетных нагрузок; S - статический момент сдвигаемой части сечения относительно нейтральной оси; J - момент инерции сечения относительно нейтральной оси; t - толщина стенки в плоскости сдвига; Rs - расчетное сопротивление металла сдвигу.
При действии изгибающих моментов в двух плоскостях ( случай косого изгиба) проверка нормальных напряжений выполняется по соотношению:
где Mx , My, Wnx, Wny - изгибающие моменты и моменты сопротивления сечения относительно осей изгиба X и Y.
По мере роста нагрузки в сечении изгибаемого элемента могут развиваться пластические деформации. Развитие пластических деформаций в сечении изгибаемого элемента иллюстрируется эпюрами на рис. 4.2.
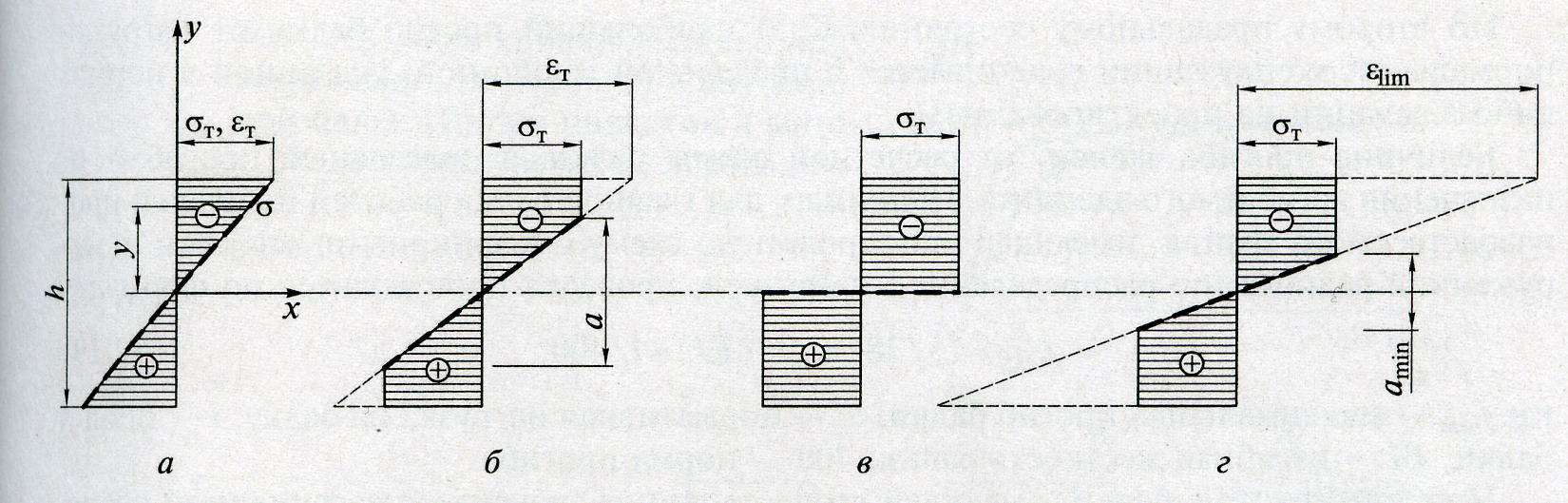
Рис.4.2. Изменение эпюры напряжений в изгибаемом элементе при развитии
пластических деформацйий в материале
а – в упругой стадии, б – в упруго-пластической, в – шарнир пластичности, г – при ограниченной пластичности
При проверке прочности с учетом пластических деформаций, формула получается из соотношения ( 4.4 ) заменой величины Wn на величину Wn,пл = C Wn .
где коэффициент c учитывает увеличение момента сопротивления и определяется по нормам. Кроме того это соотношение разрешается применять только для случаев
когда τ ≤ 0,9 Rs . А проверка прочности на сдвиг в этом случае производится только в опорных сечениях разрезных балок, там где изгибающие моменты равны нулю. Для тавровых балок проверка производится при τ ≤ 0,5 Rs по соотношению
где t - толщина стенки; h - высота балки.
Для случая косого изгиба при τ ≤ 0,5 Rs проверка производится по соотношению:
где Сx и Сy коэффициенты зависящие от формы сечения; β - коэффициент меньший единицы и зависит от величины касательного напряжения τ. При работе элементов металлических конструкций возможны случаи сложного напряженного состояния когда совместно действуют изгиб и усилия растяжения или сжатия. В общем случае, когда действует осевая сила N и моменты в двух направлениях Mx и My предельную несущую способность проверяют по формуле:
где An , Wnx , Wny - площадь и соответстующие моменты сопротивления нетто поперечного сечения стержня; Сx и Сy - коэффициенты, учитывающие увеличение несущей способности материала при развитии пластических деформаций; n - показатель степени. Три последние величины принимаются в соответстии с действующими нормами. Для конструкций работающих в упругой стадии и в случаях когда развитие пластических деформаций недопустимо, в проверочной формуле следует положить n = Сx = Сy= 1 и соотношение ( 4.10 a ) перейдет в соотношение для проверки по упругой стадии работы материала при действии нормальной силы и изгиба в двух плоскостях:
В случае действия сжимающей силы и изгиба в двух направлениях может также произойти потеря устойчивости и при этом необходимо произвести соответствующие проверки. Потеря устойчивости может произойти как в плоскости действия момента, так и из плоскости, это зависит от соотношения гибкостей стержня в этих плоскостях. Формула проверки устойчивости в этом случае аналогична формуле проверки для случая продольного изгиба: N / ( φe A ) ≤ Ry γc , ( 4.11 )
Однако коэффициент потери устойчивости φe зависит в данном соотношении от приведенной гибкости ef . Способ вычисления этих величин приведен в нормах. Проверка на устойчивость из плоскости действия момента производится по формуле:
Расчет изгибаемых элементов
Изгибаемые элементы рассчитывают по первой группе предельных состояний, когда проверяют их прочность и устойчивость, и по второй группе предельных состояний, когда проверяют их жесткость (прогиб). Расчеты на прочность и устойчивость ведут по расчетным нагрузкам, а расчет на прогиб — по нормативным.
Прочность изгибаемых элементов проверяют по нормальным касательным и приведенным напряжениям. Если балка работает на изгиб в одной из главных плоскостей (рисунок ниже, слева) в пределах упругости, то в сечениях балки получается треугольная эпюра нормальных напряжений (рисунок ниже, справа).
Работа балки на изгиб

а — расчетная схема и эпюры моментов и поперечных сил; б— поперечное сечение и эпюры нормальных и касательных напряжений
Максимальное значение этих напряжений в крайних волокнах
где М—расчетный изгибающий момент; Wnmin — наименьшее значение момента сопротивления с учетом ослаблений.
Касательные напряжения в изгибаемых элементах проверяют в местах наибольшей поперечной силы Q но формуле
где Q — расчетная поперечная сила; Sx — статический момент сдвигаемой части сечения относительно нейтральной оси; Jx — момент инерции (брутто) всего поперечного сечения балки; tω — толщина элемента в месте, где проверяют касательные напряжения (обычно толщина стенки по нейтральному слою); Rs ≈ 0,58Ry — расчетное сопротивление стали на сдвиг.
При ослаблении стенки балки отверстиями для болтов значения τ в формуле ниже следует умножать на коэффициент:
Здесь а — шаг отверстия; d — диаметр отверстий.
Для стенок балок, рассчитываемых по формуле выше делают проверку по приведенным напряжениям с учетом совместного действия нормальных и касательных напряжений. В металлических конструкциях эту проверку производят по энергетической теории прочности.

где σх = M / J n x · y — нормальные напряжения в срединной плоскости стенки, параллельные оcи балки; σy. — то же, перпендикулярные оси балки, в том числе σloc, определяемое по формуле выше;
τ = Q / tωh - среднее касательное напряжение с учетом коэффициента ослаблений α (здесь t = tω и h= hω) — соответственно толщина и высота стенки).
Общую устойчивость изгибаемых элементов проверяют по первой группе предельных состояний.
Под влиянием нагрузки, расположенной в плоскости одной из главных осей инерции поперечного сечения, балка изгибается в этой плоскости лишь до достижения нагрузкой некоторого критического значения. Затем балка выходит из плоскости изгиба и начинает закручиваться. Это явление называют потерей общей устойчивости балки, а соответствующий ему изгибающий момент — критическим моментом. Форму потери общей устойчивости балки называют изгибно-крутильной (рисунок ниже). В поясах потерявшей устойчивость балки развиваются пластические деформации, и она быстро теряет несущую способность при нагрузке, незначительно превосходящей критическую.
Потеря общей устойчивости консольной двутавровой балки (а) и влияние места приложения нагрузки (б)

Проверка общей устойчивости сводится к сравнению возникающих напряжений с критическими: σ=M/W< σсr Критические напряжения связаны с расчетным сопротивлением материала через коэффициент (называемый «фи балочный»), в результате чего формула для проверки общей устойчивости изгибаемого элемента имеет вид:
где φb — коэффициент снижения несущей способности.
Для элементов, изгибаемых в двух плоскостях, прочность проверяют по формуле:
где х и у — координаты рассматриваемой точки сечения относительно главных осей.
При этом значения напряжений в стенке балки должны быть проверены по формулам выше в двух плоскостях изгиба.
Расчет в опорном сечении балок (при М = 0; Мх = 0; Мy= 0) следует выполнять по зависимости:
Расчет стальных изгибаемых элементов по второй группе предельных состояний сводится, в первую очередь, к проверке условия:
где f— фактический прогиб, определяемый от действия нормативных нагрузок по правилам сопротивления материалов без учета ослаблений отверстиями для болтов и без учета коэффициента динамичности; l = lef— расчетный пролет изгибаемого элемента; fu/l — предельно допустимый относительный прогиб, принимаемый для промышленных и гражданских зданий.
Прогиб балок от нормативных нагрузок определяют по формулам строительной механики, пренебрегая ослаблением отверстиями для болтов.
Если балка подвергается изгибу в двух главных плоскостях (косой изгиб), то ее прочность
Методы расчета металлических конструкций по предельным состояниям. Расчетные сопротивления
Металлические конструкции рассчитывают на все виды силовых воздействий по методу предельных состояний. Сечения по методу предельных состояний выбираются минимально необходимыми при воздействии на них максимально возможной силы в самых неблагоприятных условиях работы.
При расчете конструкций по первой группе предельных состояний (по несущей способности) условие прочности с учетом коэффициентов надежности в общем виде можно представить функцией

где ∑Nnγfγlc — расчетное усилие, полученное от различных нагрузок со своими коэффициентами надежности по нагрузкам и сочетаний; Ф — функция несущей способности; S — геометрические характеристики сечения. Смысл этой формулы состоит в том, что наибольшее внешнее расчетное усилие не должно превышать наименьшую несущую способность.
За нормативное сопротивление металла Ryn как правило, принимают наименьшее значение предела текучести, гарантированное соответствующими ГОСТами и ТУ, т. е. Ryn = σy.
Для хрупких металлов, а также в тех случаях, когда эксплуатация конструкций, работающих на растяжение, возможна и после достижения металлом предела текучести, за величину нормативного сопротивления Run принимают наименьшее значение временного сопротивления на разрыв (предел прочности), т. е. Run = σu. Расчетное сопротивление Ry или Ru (по пределу текучести или по временному сопротивлению) определяют делением нормативного сопротивления на коэффициент надежности по материалу γm> 1. Для различных марок сталей значение γm меняется от 1,025 до 1,15.
Особенности работы сооружений, элементов и их соединений, не отражаемые в расчетах прямым путем, учитывают коэффициентами условий работы γc, который вводится, например, при расчете балок, сжатых элементов решетчатых конструкций, гидротехнических сооружений. Некоторые значения γc приведены ниже.
Элементы конструкций. γc
Сплошные балки и сжатые элементы ферм перекрытий под различными залами при весе
перекрытий, равном или большем полезной нагрузки. 0,9
Колонны общественных зданий и опор водонапорных башен. 0,95
Сжатые основные элементы (кроме опорных) решетки составного таврового сечения из уголков сварных ферм покрытий и перекрытий (например, стропильных и аналогичных им ферм) при гибкости λ > 60. 0,8
Сплошные балки при расчетах на общую устойчивость. 0,95
Затяжки, тяги, оттяжки, подвески, выполненные из прокатной стали. 0,9
Сжатые элементы из одиночных уголков, прикрепляемые одной полкой (для неравнополочных уголков только меньшей полкой), за исключением сжатых элементов решетки пространственных решетчатых конструкций и плоских ферм из одиночных уголков 0,75
Примечания. 1. Коэффициенты условий работы при расчете одновременно учитывать не следует. 2. Коэффициенты условий работы при расчете соединений рассматриваемых элементов учитывать не следует.
В гидротехнических сооружениях коэффициенты условий работы отражают приведение теоретических расчетов в соответствии с действительными условиями работа конструкций, учитывают возможные отступления действительной конструкции от спроектированной (в пределах допусков, определяемых ТУ на изготовление и монтаж механического оборудования и стальных конструкций гидротехнических сооружений). Кроме того, этот коэффициент учитывает возможность появления не предусмотренных расчетом различных неблагоприятных условий работы конструкции и условность расчетной схемы. Для большинства затворов принимают коэффициент условий работы γc = 0,72.
Для элементов конструкций, рассчитываемых на прочность по временному сопротивлению, следует дополнительно учитывать коэффициент надежности γu = 1,3.
Расчетные сопротивления для проектирования стальных конструкций зданий и сооружений, изготовляемых из проката и труб, для различных видов напряженных состояний определяют по следующим формулам:
С учетом коэффициентов надежности по материалу, временному сопротивлению, условий работы, по назначению окончательная формула расчетного сопротивления имеет вид:
В таблице ниже приведены расчетные сопротивления некоторых марок строительных сталей.
Читайте также:
