Расчет балки стальной балки покрытия
Прогон — это несущий элемент конструкции здания. Прогон поддерживает кровлю или пол и передает нагрузку на стены, балки или стропильную ферму.
В данной статье мы рассмотрим прогоны в промышленных зданиях из прокатных профилей, алгоритм прочностного расчета погона и балки, ответим на вопрос: «Какой профиль применять эффективнее?».
В СНиП II-23-81* (Стальные конструкции) расчет прогонов производился без учета действия бимомента, в СП 16.13330.2011 (Актуализированной редакции СНиП II-23-81*) появилось требование учета бимомента. Давайте разберемся в чем заключается учет бимомента при расчете балок и прогонов. Хотя новый СП пока носит рекомендательный характер, но вскоре он будет обязателен к применению.
При нагрузке профиля, расположенного под углом или при не равномерной нагрузке на профиль образуется изгибно-крутящий момент, который называется бимомент.
Очень подробно о расчете балок и прогонов с учетом бимомента расписано в книге «Строительная механика стержневых тонкостенных конструкций. Д.В.Бычков 1962.»
Расчет на изгиб согласно СНиП II-23-81*
Рассмотрим следующий вариант нагружения:
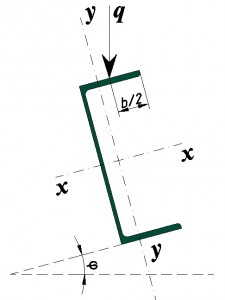
Расчет на прочность при изгибе в 2-х главных плоскостях рассчитывается по формуле 38 (СНиП II-23-81*)
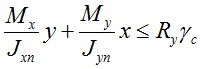
Mx и My — значения изгибающих моментов вокруг оси x-x и y-y;
Jxn и Jyn — момент инерции сечения нетто вокруг оси x-x и y-y;
x и y — расстояние от центра масс до рассматриваемой точки;
Ry — расчетное сопротивление стали изгибу;
γс — коэффициент условий работы.
Т.к. максимальное значение напряжение возникает при максимальных значениях x и y, тогда:
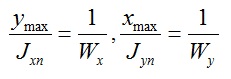
Переместив Ry и γс в левую часть уравнения, получим формулу для проверки прочности элемента конструкции:
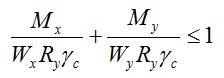
Для равномерно-нагруженной балки максимальный момент равен:
Для прогона расположенного под наклоном формулы для определения моментов будут выглядеть следующим образом:
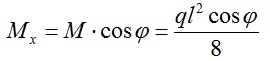
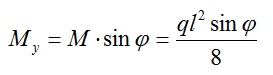
Wx и Wy — моменты сопротивления сечения, определяются согласно ГОСТ-у на прокат.
Ry — расчетное сопротивление стали определяется исходя из принятой марки стали согласно приложению 1 СНиП II-23-81*.
Коэффициент условий работы (γс) задается согласно таблице 6 СНиП II-23-81 и, в зависимости от назначения балки, равен от 0,9 до 1,1.
При угле наклона равной нулю My будет равен нулю, а Мx примет максимальное значение.
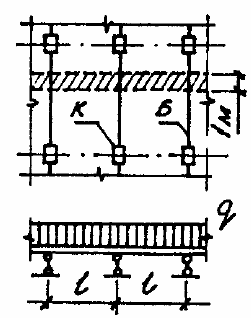
При увеличении угла наклона Mx уменьшается,а My увеличивается. В качестве прогона кровли обычно применяют швеллер, для него Wx имеет значение в несколько раз большее чем Wy. Для балки самым главным является значение Wx т.к. основной задачей балки является сопротивление изгибу в главной плоскости, но с увеличением угла изгибающий момент My увеличивается и это становится критическим фактором и необходимо увеличивать сечение. Для того, чтобы уменьшить момент My при больших уклонах применяют тяжи. Тяжи это элемент конструкции кровли, применяемый для уменьшения скатной составляющей момента. Схему расположения тяжей показана на следующих рисунках:
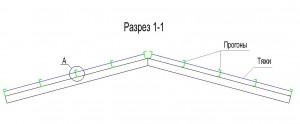
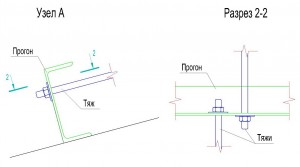
Верхний прогон тяжами не закрепляется т.к. нагрузка на него меньше, и покрытие кровли сможет обеспечить необходимую прочность. Тяжи делают из проката круглого сечения, в обычных ситуациях диаметр принимается 16 мм. Установка тяжей позволяет уменьшить изгибающий момент My.
Если тяжи делят прогон на 2-е части, то эпюра моментов будет соответствовать эпюре моментов 2-х пролетной балки, формула вычисления My будет выглядеть следующим образом:
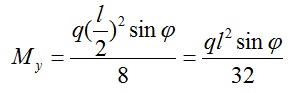
Если тяжи делят прогон на 3-и части, то эпюра моментов будет соответсовать эпюре 3-х пролетной балки. Здесь есть интересный момент, при максимальном изгибающем моменте Mx изгибающий момент My не принимает своего максимального значения. В середине пролета My равен:
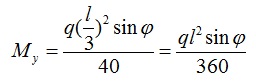
Максимальное значение My будет в точках крепления тяжей, здесь My принимает значение:
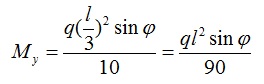
Изгибающий момент Mx в точке крепления тяжа примет значение :
Необходимо проверить оба условия.
Использование тяжей даже при угле 5 градусов дает прирост несущей способности 30 % по сравнению с прогоном без использования тяжей, поэтому их использование более чем оправданно. На более больших углах наклона использовать тяжи просто необходимо.
Расчет на изгиб согласно СП 16.133330.2011
Расчет на изгиб согласно СП 16.13330.2011 производится по формуле 43:
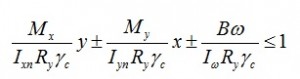
γс — коэффициент условий работы;
Jω-секториальный момент инерции;
1 — просто единица :).
Первые 2-а слагаемые мы уже разобрали, 3-е слагаемое это расчет напряжения в сечении при действии бимомента.
Бимомент возникает при скручивании профиля, но не обязательно необходимо прикладывать крутящий момент к профилю чтобы появился бимомент. При приложении нагрузки не через центр масс или при наклоне профиля возникают силы, скручивающие профиль. Если не учитывать эти силы, то профиль, особенно тонкостенный, может не выдержать нагрузки и закрутиться — это явление называют депланацией сечения. Мы разберем расчет прогона из швеллера при различных углах наклона.
Расчет бимомента B производим согласно методике, написанной в книге Д.В.Бычкова «Строительная механика стержневых тонкостенных конструкций».
Бимомент при равномерно-распределенной нагрузке вычисляется согласно формуле в Приложении 12 Д.В.Бычкова «Строительная механика стержневых тонкостенных конструкций»:
α — это не угол, а коэффициент, определяемый согласно графика для определения расчетных изгибно-крутящих бимоментов (Приложение 12);
q — равномерно-распределенная нагрузка;
e — эксцентриситет приложения нагрузки относительно оси вращения;
l — длина стержня.
На следующем рисунке представлена схема нагружения швеллера:
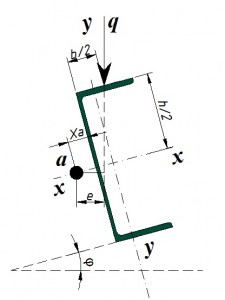
Коэффициент α определяется согласно следующему графику:
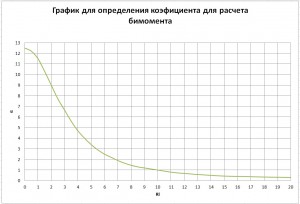
R — коэффициент, который можно найти в Приложении 3, таблице 4 Руководства по подбору сечений элементов строительных стальных конструкций, это значение равно:
Перемножаем эти 2-а значения и по графику определяем значение α.
Нагрузку q разлагать по оси х-х и у-у не нужно.
Эксцентриситет для варианта представленного на рисунке вычисляется по формуле:
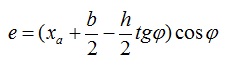
Jω-секториальный момент инерции и ω-секториальная площадь определяются согласно Приложению 3, таблице 4 Руководства по подбору сечений элементов строительных стальных конструкций.
Точки расположения секториальных площадей показаны на следующем рисунке
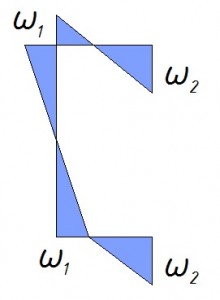
Чтобы рассчитать балку на изгиб с учетом бимомента нам необходимо сделать расчет для 4-х точех. Для балки с равномерно-распределенной нагрузкой без тяжей знаки для составляющих формулы 43 СП 16.13330.2011 будут выглядеть следующим образом:
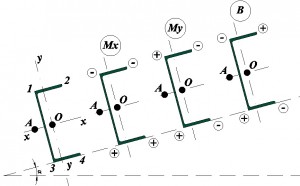
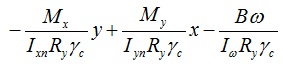
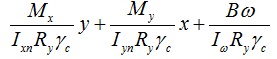
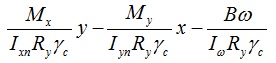
Стоит отметить, что в данном случае бимомент разгружает профиль, т.е. если расчитывать без учета бимомента, то несущая способность профиля будет ниже.
Расчет прогона с учетом бимомента с раскреплением тяжами не рассмотрен т.к. этой методики в книге Бычкова нет, но я постараюсь найти методику расчета.
Также необходимо проверить прогоны на прочность при поперечной силе, расчет на прочность при действии сосредоточенной силы, расчет на прочность в опорном сечении и проверить прогиб. Методику расчета вы можете найди в моей предыдущей статье Расчет балки , но, как правило, самым критическим фактором является расчет на изгиб.
Итог:
В итоге мы видим что учет бимомента разгружает профиль, но пока новый СП 16.13330.2011 носит лишь рекомендательный характер, поэтому прогон необходимо считать по СНиП II-23-81*.
Для расчета прогонов я сделал программку в Excel, которая позволяет подобрать необходимый прогон из швеллера для кровли, скачать ее можно здесь
Расчет балки стальной балки покрытия
Перед началом расчета стальной балки необходимо собрать нагрузку, действующая на металлическую балку. В зависимости от продолжительности действия нагрузки разделяют на постоянные и временные.
К постоянным нагрузкам относятся:
- собственный вес металлической балки;
- собственный вес перекрытия и т.д.;
К временным нагрузкам относятся:
- длительная нагрузка (полезная нагрузка, принимается в зависимости от назначения здания);
- кратковременная нагрузка (снеговая нагрузка, принимается в зависимости от географического расположения здания);
- особая нагрузка (сейсмическая, взрывная и т.д. В рамках данного калькулятора не учитывается);
Нагрузки на балку разделяют на два типа: расчетные и нормативные. Расчетные нагрузки применяются для расчета балки на прочность и устойчивость (1 предельное состояние). Нормативные нагрузки устанавливаются нормами и применяется для расчета балки на прогиб (2 предельное состояние). Расчетные нагрузки определяют умножением нормативной нагрузки на коэффициент нагрузки по надежности. В рамках данного калькулятора расчетная нагрузка применяется при определении прогиба балки в запас.
Нагрузки можно собрать на нашем сайте.
После того как собрали поверхностную нагрузку на перекрытие, измеряемой в кг/м2, необходимо посчитать сколько из этой поверхностной нагрузки на себя берет балка. Для этого надо поверхностную нагрузку умножить на шаг балок(так называемая грузовая полоса).
Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 500кг/м2, а шаг балок 2,5м. Тогда распределенная нагрузка на металлическую балку будет: Qраспр.= 500кг/м2 * 2,5м = 1250кг/м. Эта нагрузка вносится в калькулятор
2. Построение эпюр
Далее производится построение эпюры моментов, поперечной силы. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.
3. Расчет по прочности и прогибу
После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и из таблицы сортамента выбрать подходящий металлопрофиль. Вертикальный предельный прогиб fult принимается по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия). Пункт2.а в зависимости от пролета. Например предельный прогиб fult=L/200 при пролете L=6м. означает, что калькулятор подберет сечение прокатного профиля (двутавра, швеллера или двух швеллеров в коробку), предельный прогиб которого не будет превышать fult=6м/200=0,03м=30мм. Для подбора металлопрофиля по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента подбирают подходящий металлопрофиль.
4. Подбор металлической балки из таблицы сортамента
Из двух результатов подбора (1 и 2 предельное состояние) выбирается металлопрофиль с большим номером сечения.
Нагрузки, действующие на перекрытие и покрытие здания разделяют на постоянные и временные. Вид нагрузки зависит от времени, которое действует на конструкцию
- собственный вес плиты, балки, вес элементов пола, перегородки;
- длительная нагрузка (полезная нагрузка, зависит от назначения здания);
- кратковременная нагрузка (снеговая, которая берется по климатическим картам из СНиП "Нагрузки и воздействия");
- особая нагрузка (сейсмическая, взрывная и т.д.);
Нагрузки бывают двух типов: нормативные и расчетные.
Нормативные нагрузки берутся из СНиП "Нагрузки и воздействия" с учетом возможного отклонения в большую сторону от фактического значения.
Расчетные нагрузки получают путем умножения нормативной нагрузки на коэффициент надежности по нагрузки. Этот коэффициент учитывает неточности монтажа конструкций, погрешности при производстве на стройке, а также человеческий фактор. Своего рода этот коэффициент является по своей сути коэффициентам запаса. Таким образом, для конструкций, произведенных в заводских условиях коэффициент запаса будет равен 1.1, а для конструкции, производимые на строительной площадке, например стяжка для пола, коэффициент запаса будет равен 1,3.
Как правильно собрать нагрузку на балку и плиту для дальнейшего расчета:
Для балки. Чтобы правильно собрать нагрузку на балку - нужно представить, сколько из общей равномерно распределенной нагрузки q(кг/м2) на себя будет брать балка. Логично предположить, что нагрузка с плиты передается на балки, потом с балки нагрузка передается на колонны и дальше, через колонны, нагрузка передаётся на фундамент. Поэтому нагрузка распределяется поровну на соседние балки, таким образом ширина действия нагрузки на балку 'В' равна l2/2 + l2/2 или проще В=l2 - для средних балок и l2/2 для крайних балок перекрытия, где l2 равен шагу балок. Поэтому допускается делать крайние балки меньшего сечения, но для унифицирования делают такого же сечения или бывает, что в крайних балках могут возникнуть дополнительные усилия, например от кручения или продольные усилия от ветра. Таким образом погонная нагрузка (q1), именуемая в литературе "грузовая полоса", действующая на балку равна q1=q*B(кг/м), где q=равномерно распределенная нагрузка.
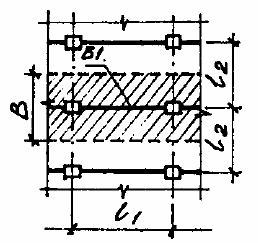
Для плиты. Чтобы проще было рассчитать плиту перекрытия, опертую на балки - мысленно "вырезают" из распределенной нагрузки q(кг/м2) площадку шириной 1м и умножают на ширину вырезанной площадки, то есть на 1м. Соответственно плиту считают как многопролетную неразрезную балку шириной 1м, на которую действует погонная нагрузка q1(кг/м), а балки, на которую опирается плиты - являются для плиты шарнирными опорами. Например, если получили распределенную нагрузку на плиту q=0,5т/м2. То погонная нагрузка на плиту будет составлять q1=0,5т/м2*1м=0,5т/м.
Калькулятор нагрузок на перекрытие, балку перекрытия
Данный калькулятор позволяет в табличной форме посчитать суммарную равномерно-распределенную нормативную и расчетную нагрузку на перекрытие, покрытие, плиту, балку.
Чтобы посчитать сечение деревянной балки - необходимо собрать нагрузку, действующая на балку. В зависимости от длительности действия нагрузки разделяют на постоянные и временные.
- собственный вес деревянной балки;
- собственный вес перекрытия, чердачного перекрытия и т.д.;
Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 400кг/м2, а шаг балок 0,6м. Тогда распределенная нагрузка на деревянную балку будет: Qраспр.= 400кг/м2 * 0,6м = 240кг/м. Эта нагрузка вносится в калькулятор
2. Выбор предельного прогиба
В зависимости от назначения балки и ее пролета задаем вертикальный предельный прогиб по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия) Пункт2.а. Смысл вертикального прогиба заключается в следующем: например, прогиб l/250 означает, что для балки длинной 4м предельный вертикальны прогиб равен fult = 4м / 250 = 0,016м = 16мм в месте максимального прогиба для балки. Для балки на двух опорах загруженной равномерно или с сосредоточенной нагрузкой посередине балки - максимальный прогиб будет посередине пролета. Для консольной балки максимальный прогиб - на свободном конце балки.
3. Задание ширины искомого сечения балки.
В зависимости от конструктивных требований задаем ширину сечения балки. Расчет деревянной балки сводится к тому, что необходимо подобрать требуемую высоту hтр сечения деревянной балки, которое способно выдержать заданную нагрузку и не превысить заданный предельный прогиб.
Алгоритм расчета деревянной балки, используемый в данном калькуляторе
По заданной нагрузке и пролету производится построение эпюры моментов и поперечной силы. Эпюра поперечной силы находится для информации (чтобы знать какая нагрузка давит на опоры балки) и в расчете не используется. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.
2. Расчет по прочности и прогибу
После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и hтр и из таблицы рекомендуемого сортамента выбрать подходящее сечение высотой равное hтр деревянной балки по ширине сечения (b) и по Wтр. Следует отметить, что калькулятор подбирает именно по Wтр, нахождение hтр сделано для наглядности, чтобы видеть какая высота сечения должна быть. Для подбора деревянной балки по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента пиломатериалов подбирают подходящее сечение.
3. Подбор деревянной балки из таблицы сортамента пиломатериалов по ГОСТ 244454-80
Из двух результатов подбора (1 и 2 предельное состояние) выбирается сечение с большей выстой сечения.
Расчет балки
При расчете стальных балок необходимо руководствоваться СП 16.13330 «Стальные конструкции».
В данном обзоре я рассмотрю расчет балок 1-го класса напряженно-деформированного состояния (напряжения по всей площади напряжения не превышают расчетного сопротивления стали). Расчёт подкрановых, бистальных, защемленных и многопролетных балок будет рассмотрен отдельно.
Элементы конструкции должны иметь запас прочности по 1-му и 2-му предельному состоянию.
По 1-му предельному состоянию проверяется прочность элементов. Нагрузки для расчета по 1-му предельному состоянию выше, чем по 2-му предельному состоянию т.к. используются коэффициенты запаса для нагрузок.
По 2-му предельному состоянию проверяются деформации конструкции.
Расчеты по 1-му предельному состоянию:
- Расчет на прочность при действии изгибающего момента
- Расчет на прочность при действии поперечной силы
- Расчет на прочность стенки балки при действии сосредоточенной силы
- Расчет на прочность в опорном сечении
- Расчет на общую устойчивость
- Расчет на устойчивость стенок и поясных листов балки
Расчеты по 2-му предельному состоянию:
1. Расчет на прочность при действии изгибающего момента
В первую очередь необходимо подобрать балку по изгибающему моменту.
Прочность стальной балки на изгиб проверяется по следующей формуле (п.8.2.1 СП 16.13330.2011 или 5.12 СНиП II-23-81*):
где M – максимальный момент, возникающий в балке (находится по эпюре моментов);
Wn,min – момент сопротивления сечения (находится по таблице или вычисляется для данного профиля), у сечения обычно 2-а момента сопротивления сечения, в расчетах используется Wx если нагрузка перпендикулярна оси х-х профиля или Wy если нагрузка перпендикулярна оси y-y;
Ry – расчетное сопротивление стали при изгибе (задается в соответствии с выбором стали);
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП 16.13330.2011 Стальные конструкции либо таблице 6* СНиП II-23-81) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Из этой формулы можно вычислить минимально требуемый момент сопротивления сечения.
Вначале вычисляем максимальный момент от нагрузок. На этом этапе мы еще не знаем массу балки и ее можно не учитывать при предварительном расчете.
Далее выбираем марку стали. При выборе марки стали необходимо учитывать класс конструкции и климатические условия эксплуатации – если конструкция эксплуатируется в холодном климате в неотапливаемом здании, то марка стали не должна быть хрупкой. Прочность стали выбирается исходя из экономического расчета – несмотря на то, что с увеличением марки стали ее стоимость увеличивается, сечение балки из более прочной стали может быть меньше и соответственно будут меньше нагрузки. Для того, чтобы выбрать оптимальную марку стали необходимо сделать несколько расчетов и оценить их.
После того, как мы предварительно рассчитали минимальный момент сопротивления сечения (Wn) подбираем из сортамента профиль, имеющий W не много выше чем требуемый и имеющий наименьшую массу. Для балок оптимальным профилем является двутавр, швеллер. Возможно использование составного сечения из листов. При расчете важно правильно учесть положение профиля – Wx используется, если ось x-x перпендикулярна направлению приложения нагрузки. Соответственно профиль необходимо располагать так, чтобы момент сопротивления сечения был максимальным (от того как расположить профиль многое зависит).
После выбора сечения необходимо прибавить к изгибающему моменту момент, создаваемый массой балки и вновь проверить сечение.
Если балка расположена под углом, то расчет прочности при изгибе производят по следующей формуле:
где требуется разложить силу на направляющие по оси х-х и у-у и отдельно вычислить максимальные моменты Mx и My вокруг оси х-х и у-у соответственно.
В СП 16.13330.2011 дополнительно требуют учитывать бимомент, формула выглядит следующим образом:
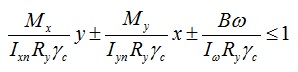
x и y — расстояния от главных осей до рассматриваемой точки;
Ixn,Iyn — моменты инерции сечения, находятся по таблице согласно ГОСТ-у на выбранный профиль;
Iω — секториальный момент инерции сечения, можно найти в приложении 3 руководства по подбору сечений стальных конструкций;
ω — секториальная площадь.
Здесь рассматриваются несколько точек, как правило 4 крайние точки профиля и для них проверяют условия, знаки подбирают согласно эпюрам напряжения. Подробно расчет профилей с учетом бимомента расписано в книге Д.В.Бычкова Строительная механика стержневых тонкостенных конструкций.
Для прогонов наклонной кровли из швеллера для упрощения расчета бимомент можно не учитывать т.к. он разгружает профиль на 10-15%, и это будет запасом прочности. В других случаях рекомендуется принимать конструктивные меры препятствующие возникновению закручивающего момента.
2. Расчет на прочность при действии поперечной силы
Далее необходимо проверить профиль на действие касательных (поперечных) сил по формуле:
где Q – наибольшая поперечная сила (можно определить согласно эпюре Q), для балки наибольшее значение получается на опорах;
S – статический момент сдвигаемой части сечения (определяется по таблице для выбранного профиля);
I – момент инерции сечения (определяется по таблице для выбранного профиля);
tw – толщина стенки балки;
Rs — расчетное сопротивление стали сдвигу, равно 0,58 от Ry согласно Таблице 2 СП 16.13330.2011;
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП Стальные конструкции) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Если профиль не удовлетворяет условию, то необходимо увеличить сечение.
3. Расчет на прочность стенки балки при действии сосредоточенной силы
Расчет на прочность стенки балки, не укрепленной ребрами жесткости, при действии сосредоточенной силы и в опорных сечениях определяют по формуле:
здесь F – расчетное значение нагрузки;
lef – условная длина распределения нагрузки;
tw – толщина стенки балки.
Условную длину распределения нагрузки можно определить по формуле
для следующих случаев:
для прокатной балки:
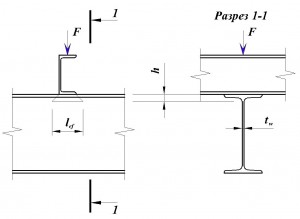
где b – ширина полки швеллера
h – сумма толщины верхней полки и радиуса закругления
для сварной балки:
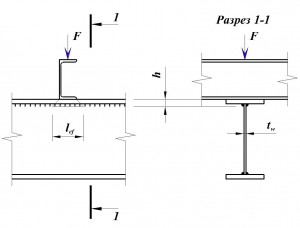
где h – сумма толщины верхней полки и катета сварного шва.
4. Расчет на прочность в опорном сечении
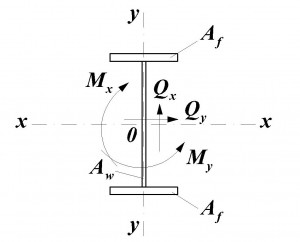
Расчет на прочность в опорном сечении балки (при Mx=0 и My=0) следует определять по формулам:
где Aw– площадь сечения стенки,
Af– площадь сечения полки,
Rs–расчетное сопротивление стали сдвигу.
При ослаблении стенки отверстиями для болтов левую часть формулы необходимо умножить на коэффициент α, который находиться по формуле:
где s – шаг отверстий в одном ряду;
d – диаметр отверстия.
Расчет на прочность для защемленных и неразрезных балок мы рассмотрим отдельно.
5. Расчет на общую устойчивость
Далее необходимо проверить балку на устойчивость.
Данный расчет можно не выполнять:
а) при передаче нагрузки через сплошной жесткий настил (плиты железобетонные, плоский или профилированный металлический настил, волнистая сталь и т.п.), непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (с помощью сварки, болтов, самонарезающих винтов), при этом силы трения учитывать не стоит;
б) если условная гибкость сжатого пояса балки меньше предельных значений. Условная гибкость вычисляется по формуле:
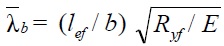
Предельное значение гибкости пояса вычисляется по формулам:
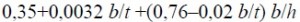
при приложении нагрузке к верхнему поясу
при приложении нагрузке к нижнему поясу
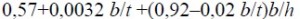
независимо от уровня приложения нагрузки при расчете участка балки между связями или при чистом изгибе
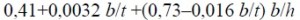
где b – ширина сжатого пояса;
t – толщина сжатого пояса;
h – расстояние (высота) между осями поясных листов.
- Значения предельной гибкости определены при 1≤ h/b ≤6 и 15≤ b/t ≤35; для балок с отношением b/t
- Для балок с фрикционными поясными соединениями предельную гибкость следует умножать на 1,2
Проверка общей устойчивости при изгибе в плоскости стенки, совпадающей с плоскостью симметрии сечения, осуществляется по следующей формуле:
если изгиб происходит в 2-х плоскостях (и наличии секториальных напряжений), тогда проверку осуществляют по формуле:
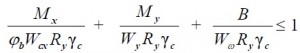
где φb – коэффициент устойчивости при изгибе, подробный расчет коэффициента устойчивости (φb) приведен в приложении Ж СП 16.13330.2011 Стальные конструкции;
Wcx – момент сопротивления сечения относительно оси x-x, вычисленного для сжатого пояса;
Wy – момент сопротивления сечения относительно оси y-y, совпадающий с плоскостью изгиба;
Wω – секторальный момент сопротивления сечения.
При расчете значения φbза расчетную длину балки lef следует принимать расстояние между точками закрепления сжатого пояса от поперечных смещений. При отсутствии связей lef=l (где l – пролет балки).
Если в процессе расчета выясняется, что общая устойчивость балки не обеспечивается, то следует уменьшить расчетную длину сжатого пояса, изменив систему связей.
6. Расчет устойчивости стенок и поясных листов балки
Устойчивость стенок балок 1-го класса следует считать обеспеченной если условная гибкость стенки, вычисленная по формуле:
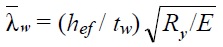
hef — расчетная высота стенки, принимаемая согласно требованиям 7.3.1 СП 16.13330.2011;
tw — толщина стенки балки;
Ry — расчетно сопротивление стали при изгибе;
E — модуль упругости стали равный 210 ГПа (210 000 МПа)
Условная гибкость стенки не должна превышать значений:
3,5 – при отсутствии местного напряжения в балках с двухсторонними поясными швами;
3,2 – при отсутствии местного напряжения в балках с односторонними поясными швами;
2,5 – при наличии местного напряжения в балках с двухсторонними поясными швами.
Если условная гибкость стенки выше требуемой, то стенки необходимо усилить ребрами жесткости и сделать проверку согласно п. 8.5.3 СП 16.13330.2011.
7. Расчет прогиба балки
Расчет на 2-е предельное состояние балки заключается в расчете максимального прогиба.
Высокие деформации могут привезти к нарушению герметичности, невозможности эксплуатации, плохому эстетическому восприятию конструкции, поэтому конструкция не должна сильно деформироваться. Предельные прогибы конструкций приведены в приложении Е СП 20.13330 Нагрузки и воздействия
К примеру, для балки покрытия, длиной 6 м, предельный прогиб составляет 1/200 длины пролета т.е. 30 мм.
Формула определения прогиба зависит от способа приложения нагрузки, например однопролетной шарнирно-закрепленной с равномерно-распределенной нагрузкой прогиб рассчитывается по формуле:
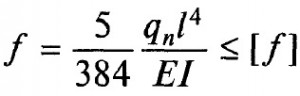
где q – равномерно-распределенная нагрузка, выраженная в кг/м (Н/м);
l – длина балки в метрах;
E – модуль упругости (для стали равен 200-210 ГПа);
I – момент инерции сечения.
Для других способов нагрузки балки формулы смотрите в справочниках по сопротивлению материалов.
Если расчетный прогиб больше допускаемого, то следует увеличить сечение балки.
Как найти расчетный момент и поперечную силу читайте в статье Построение эпюр балки
Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки
Как рассчитать балку в SCAD и подобрать сечение читайте в статье Расчет балки в SCAD
Читайте также:
