Один конец стального вертикального бруса

Обновлено: 08.01.2025

Исходные данные для выполнения индивидуальных заданий на контрольные задачи студент должен взять из приводимых таблиц и схем расчетов в строгом соответствии со своим учебным шифром.

Для этого необходимо три последние цифры своего учебного шифра написать дважды, а затем под шестью цифрами подписать первые шесть букв из русского алфавита: а, б, в, г, д, е.

Например, при шифре 1110-СТб-3125 будет выглядеть так:

а б в г д е

Тогда число над буквой а укажет номер строки данной таблицы, откуда следует брать значение соответствующей величины из столбца а, под буквой б - из столбца б и т.д.

Студенты II курса специализаций ГС, ВВ выполняют две контрольные работы. Перечень задач приведен в табл. 1.

Задача № 1

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ

Поперечное сечение бруса (рис.1) состоит из двух частей, соединенных в одно целое.

1. Вычертить схему сечения в масштабе 1:2, на которой указать положение всех осей и все размеры;

2. Найти общую площадь сечения;

3. Определить положение центра тяжести всего сечения;

4. Определить осевые и центробежный моменты инерции сечения относительно осей, проходящих через центр тяжести параллельно полкам;

5. Найти положение главных центральных осей, значения главных центральных моментов инерции, главных радиусов инерции и проверить правильность вычисления моментов инерции.

Исходные данные взять из табл.2.

Примечание. При отсутствии указанных в табл. 3 ГОСТ можно использовать ГОСТ 8509-57 и ГОСТ 8240-56.

РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОГО БРУСА

Один конец стального вертикального бруса жестко защемлен, другой - свободен. Общая длина бруса L (рис.3). Одна часть бруса, длина которой l, имеет постоянную по длине площадь поперечного сечения A₁, другая часть - постоянную площадь А₂. В сечении, отстоящем от свободного конца бруса на расстоянии c, действует сила F. Вес единицы объема материала g = 78 кН/м 3 , модуль упругости E = 2×10 5 МПа.

1. Сделать схематический чертеж бруса по заданным размерам, соблюдая масштаб длин по вертикальной оси;

2. Составить для каждого участка бруса в сечении с текущей координатой z (0£ z £ L) аналитические выражения изменения продольного усилия N_z и нормального напряжения s_z с учетом собственного веса бруса;

3. Построить эпюры продольных усилий N_z и напряжений s_z;

4. Вычислить с учетом собственного веса бруса перемещение сечения, отстоящего от свободного конца бруса на расстоянии l.

Исходные данные взять из табл. 3.

l/L,

КРУЧЕНИЕ ВАЛОВ

Стальной валик (рис. 4) закручивается двумя парами сил, действующими в крайних сечениях. Момент каждой пары сил - М.

1. Построить эпюру крутящих моментов;

2. Определить моменты сопротивления при кручении для сечений I, II, III и по наиболее опасному сечению найти допускаемую величину момента М;

3. Построить эпюры распределения касательных напряжений в сечениях I, II, III, отметив на сечениях опасные точки;

4. Построить эпюру углов закручивания, приняв начало отсчета на левом торце валика.

Модуль упругости при сдвиге для материала валика G = 8×10 4 МПа.

Примечание. Сечение III можно приближенно считать квадратным со стороной 0,8D, т.к. срезы углов весьма незначительны.

Исходные данные взять из табл. 4

ИЗГИБ БАЛОК

Для схем балок I, II и рамы III (рис. 5,6,7) требуется:

1. Вычертить расчетные схемы, указав числовые значения размеров и нагрузок;

2. Вычислить опорные реакции и проверить их;

3. Для всех схем составить аналитические выражения изменения изгибающего момента М_х и поперечной силы Q_y, а для схемы III и продольной силы N_z - на всех участках;

4. Для всех схем построить эпюры изгибающих моментов М_х и поперечных сил Q_y, а для схемы III - эпюру продольных сил N_z_.

На всех эпюрах обязательно указать числовые значения ординат в характерных сечениях участков;

5. Руководствуясь эпюрой изгибающих моментов, показать для схем I и II приблизительный вид изогнутых осей балок;

6. По опасному сечению подобрать поперечные сечения:

а) для схемы I- прямоугольное h x b при расчетном сопротивлении R_и = 16 МПа (клееная древесина); h / b= 1,5;

б) для схемы II - двутавровое (ГОСТ 8239-72) при расчетном сопротивлении

R_и = 200 МПа (сталь).

Исходные данные взять из табл. 5.

Примечание. В схеме III (рис.7): 1) нагрузку принять одну из показанных на схеме (по выбору); 2) в раме 6 прикрепление верхнего ригеля к стойке считать жестким.

ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ

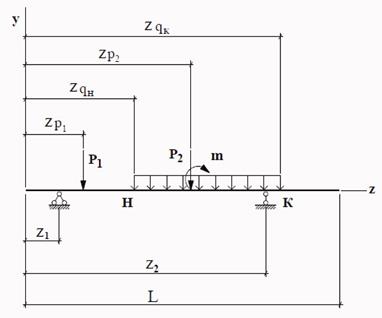
1. Нарисовать (рис. 8) схему балки, используя данные из столбцов «б» табл.6 (см. примечания к таблице).

2. Подготовить схему балки к расчету в матричной форме:

а) разделить ось балки на участки;

б) начало и конец каждого участка отметить сечениями с соответствующим номером; в) для каждого участка ввести правило знаков для ординат эпюр моментов, отложенных в сторону растянутых волокон.

3. Для выбранной балки построить эпюру изгибающих моментов от заданной нагрузки, записать её в виде матрицы – столбца и записать его в электронную таблицу EXCEL- программы ЖестБалки.xls.

4. Для определения прогиба и угла поворота сечения в точке оси с координатой Z_Р₂ приложить соответствующие единичные силовые факторы, построить от них эпюры изгибающих моментов, которые записать в виде матриц- столбцов в электронную таблицу EXCEL - программы ЖестБалки.xls в виде матрицы влияния моментов L_m.

5. В электронной EXCEL-таблице сформировать массивы по участкам балки: значений равномерно распределенных нагрузок q, EJ_прив, длин участков.

6. Выписать вычисленные программой EXCEL значения прогиба и угла поворота в заданном сечении, умноженные на модульную жесткость EJ _Л.

7. Вычислить действительные значения искомых перемещений, приняв значение EJ_Л из ячейки К6 электронной таблицы

Исходные данные взять из табл. 6.

1. L – полная длина балки; z₁- расстояние от левого края балки до шарнирно неподвижной опоры; z₂ - расстояние от левого края балки до шарнирно подвижной опоры. Расстояния от левого края балки: z_Р1 – до силы Р₁ , z_Р2 – до силы Р₂ , z_q_Н – до начала действия равномерно распределенной нагрузки q , z_q_К – до конца действия равномерно распределенной нагрузки q. Сосредоточенные силы и распределенные нагрузки считаются положительными, если они направлены вниз, Положительный сосредоточенный момент направлен по часовой стрелке. Точка приложения сосредоточенного момента m совпадает с точкой приложения силы Р₂ .

2. Принято, что от левого конца балки до точки приложения Р₂ балка имеет сечение с моментом инерции J_Л , а остальная часть балки имеет сечение с моментом инерции J_пр.

3. В программе ЖестБалки.xls предусмотрено максимальное количество участков 7. В случае меньшего количества участков, оставшиеся ячейки EXCEL- таблицы заполняются нулями.

4. EXCEL- программа ЖестБалки.xls записана в файле ЖестБалки.xls .

СОВМЕСТНОЕ ДЕЙСТВИЕ ИЗГИБА И КРУЧЕНИЯ

Пространственный консольный брус с ломаным очертанием осевой линии нагружен сосредоточенной силой F =1 кН или равномерно распределенной нагрузкой q =1 кН/м. Вертикальные элементы бруса имеют круглое поперечное сечение диаметром d, горизонтальные элементы - прямоугольное сечение (b×c). Ширина сечения b = d+20 мм, а высота сечения с = 0,5b. Размеры бруса, его поперечных сечений и внешняя нагрузка показана на рис.9.

1. Построить в аксонометрии шесть эпюр: M_x, M_y, M_z, Q_x, Q_y, N_z;

2. Указать вид сопротивления для каждого участка бруса;

3. Определить на каждом участке нормальные напряжения от совокупности внутренних усилий N_z, M_x, M_y и касательные напряжения от крутящего момента M_z (напряжениями от Q_x и Q_y можно пренебречь);

4. Найти расчетное напряжение по III теории прочности на участке, где возникают одновременно нормальные и касательные напряжения.

РАСТЯЖЕНИЕ И СЖАТИЕ ПРЯМОГО БРУСА

Требуется:

2. Составить для каждого участка бруса в сечении с текущей координатой z (0£ z £ L) аналитические выражения изменения продольного усилия N_z и нормального напряжения s_z с учетом собственного веса бруса;

3. Построить эпюры продольных усилий N_z и напряжений s_z;

Номер	L,	с,	l/L,	A₁	A₂,	F,
строки	схемы (рис.1)	м	м	10 -4 м2	10 -4 м2	кН
0,80 0,75 0,70 0,60 0,50 0,40 0,30 0,25 0,20 0,10	0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5
е	д	г	а	е	е	в

Задача № 3

КРУЧЕНИЕ ВАЛОВ

Номер	D,	d/D	a,	c,	R_ср,,
строки	10 -3 м	10 -2 м	10 -2 м	МПа
0,3 0,4 0,5 0,6 0,8 0,3 0,4 0,5 0,6 0,8	90,0 95,0 100,0 105,0 110,0 90,0 95,0 100,0 105,0 110,0
е	д	а	б	в

Задача № 4

3. Для всех схем составить аналитические выражения изменения изгибающего момента М_х и поперечной силы Q_y, а для схемы III и продольной силы N_z - на всех участках;

4. Для всех схем построить эпюры изгибающих моментов М_х и поперечных сил Q_y, а для схемы III - эпюру продольных сил N_z_.

а) для схемы I- прямоугольное h x b при расчетном сопротивлении R_и = 16 МПа (клееная древесина); h / b= 1,5;

R_и = 200 МПа (сталь).

Номер строки	Схема I рис.5	Схема II рис.6	Схема III рис.7	c/a	Р/q a	m/qa 2	a, м	q, кН/м
1,2 1,4 1,6 1,8 2,0 1,2 1,4 1,6 1,8 2,0	0,6 0,5 0,8 1,2 1,5 1,6 1,0 1,8 2,4 2,0	0,2 0,4 0,6 0,8 1,0 0,2 0,4 0,6 0,8 1,0	0,5 1,0 1,5 2,0 2,5 1,5 2,0 1,0 2,5 0,5
а	б	в	г	д	е	д	г

ЗАДАЧИ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ 2

Задачи 61—70. Двухступенчатый стальной брус, длины ступеней которого указаны на рис. 33 (схемы I — X), нагружен силами F_t и F₃. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить пере-1ещение М нижнего торцевого сечения бруса, приняв F = 2 • 10 5 МПа. Числовые значения F₁ иF₂, а также площади поперечных сечений ступеней A_t и А₂ для своего варианта взять из табл. 4.

Задача 71. Определить допускаемое значение нагрузки F для двухступенчатого бруса (рис. 34, схема I), если [σ]=150 МПа. Определив [F], построить эпюру нормальных напряжений по длине бруса.

Задача 72. Проверить прочность стержней, удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом (рис.34, схема II), если [σ]=160 МПа. Указать, на сколько процентов стержни недогружены или перегружены.

Задача 73. Определить требуемые площади поперечных сечений обеих ступеней стального бруса (рис. 34, схема III) из условия прочности, если F=60 кН, [σ_Р]=140 МПа, [σ_с]=100 МПа. Определив площади поперечных сечений ступеней, построить эпюру нормальных напряжений по длине бруса.

Задача 74. Из условия прочности стальных стержней, удерживающих в равновесии горизонтальный жесткий брус (рис. 34, схема IV), шарнирно закрепленный одним концом, определить [q]—допускаемое значение интенсивности равномерно распределенной нагрузки на брус. Принять [σр]=16O МПа, [σс] =120 МПа.

Задача 75. Проверить прочность двухступенчатого бруса (рис. 34, схема V), верхняя ступень которого из стали, нижняя — из меди, если F = 60 кН, [σ]_ст = 160 МПа, [σ]_м = 60 МПа, Е_ст = 2 • 10(5) МПа, Ем = 1 • 10(5) МПа. Построить эпюры нормальных напряжений по длине бруса и определить, на сколько процентов каждая ступень недогружена или перегружена.

Задача 76.-Определить требуемый размер поперечного сечения стальных стержней (рис. 34, схема VI), удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом, если [σ]=160 МПа. Определив требуемое значение площади А, найти напряжения в поперечных сечениях обоих стержней.

Задача 77.Определить допускаемое значение нагрузки F для двухступенчатого бруса (рис. 34, схема VII), у которого нижняя ступень из меди, а верхняя — из стали, если [σ]_ст = 160 МПа, [σ]_м = 60 МПа, Е_ст = 2 • 10(5) МПа, Е_м = 1 • 10 5 МПа. Определив значение [F], построить эпюру нормальных напряжений по длине бруса.

Задача 78. Проверить прочность стальных стержней (рис. 34, схема VIII) удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом; [σ]= 150 МПа.

Задача 79. Определить из условия прочности требуемые площади поперечных сечений двухступенчатого стального бруса (рис. 34, схема IX), если [σ] = 160 МПа. Определив значения площадей поперечных сечений ступеней построить эпюру нормальных напряжений по длине бруса.

Задача 80. Из условия прочностей стержней, удерживающих в равновесии горизонтальную жесткую балку (рис. 34, схема X), определить допускаемое значение интенсивности q равномерно распределенной нагрузки, действующей на балку в пролёте между стержнями; [σ_Р]=160 МПа, [σ_с]=110 МПа. Определив q найти нормальные напряжения в поперечных сечениях стержней

Задача 81. Из условия жёсткости вала при [_φо]=0,4 град/м определить его диаметр, если вал должен передавать мощность Р= 15 кВт при частоте вращения 420 мин(-1). Определив требуемый диаметр, найти наибольшие касательные напряжения поперечном сечении вала при его работе в заданном режиме

Задача 82. Определить диаметр стального вала для передачи мощности P=8 кВт при частоте вращения 240 мин(-1) из условия прочности, приняв [τ] = 60МПа. Определив требуемый диаметр вала, найти угол его закручивания на длине l=300 мм.

Задача 83. При какой наименьшей угловой скорости стальной вал кольцевого сечения (d=40мм,ά=d(0)/d=0.7) может передавать мощность P=12 кВт, чтобы максимальные касательные напряжения в поперечном сечении не превышали [τк] = 40 МПа, а относительный угол закручивания был бы не более [φ0] = 1 град/м? G= 0,8 * 10(5) МПа.

Задача 84.Рассчитать наружный d и внутренний d₀ диаметры полого стального вала для передачи мощности Р= 160 кВт при частоте вращения 270 мин(-1), приняв [τ] = 35 МПа, [φ0] =0,008 рад/м, ά= d₀/d = 0,65 и G =0,8*10(5) МПа.

Задача 85. Определить из условия жесткости диаметр стального вала (G=0,8*10(5) МПа, передающего мощность Р =80 кВт при частоте вращения 300 мин(-1) , приняв [φ0] =0,5 град/м. Каким будет при этом коэффициент запаса вала по пределу текучести τ_т = 140 МПа?

Задача 86. Для передачи какой мощности при частоте вращения 240 мин -1

рассчитан стальной вал диаметром d=38мм, если [τ]=0,8*10(5) МПа, [φ0]=0,02 рад/м и G=0/8*10(5) МПа?

Задача 87. Сплошной вал, рассчитанный на передачу мощности Р = 40 кВт при частоте вращения 420 мин" 1 и [τ_к] = 35 МПа, решено заменить валом кольцевого сечения с отношением диаметров ά = d0/d=0,8. Определить диаметры кольцевого сечения вала, не снижая. его прочности по сравнению со сплошного?

Задача 88. Сплошной вал, рассчитанный из условия жесткости при [φ0] = 0,008 рад/м на передачу мощности Р =100 кВт при частоте вращения 240 мин , решено заменить стальным валом кольцевого сечения с отношением диаметров d0/d = 0,85. Определить диаметры вала кольцевого сечения не снижая его жесткости. Во сколько раз вал кольцевого сечения будет легче сплошного?

Задача 89. Определить из условия прочности при [τк] = 40 МПа требуемый диаметр вала, передающего мощность Р=120 кВт при частоте вращения 45 мин ■ Найти угол закручивания вала на длине l = 2d, где d – принятый диаметр вала.

Задача 90. Рассчитать из условия жесткости при [φ0] = 0,5 град/м требуемый диаметр вала, передающего мощность Р= 180 кВт при частоте вращения 90 мин . Определить диаметр вала, найти коэффициент запаса по пределу текучести τ_т == 135 МПа; G = 0,8 • 10(5) МПа.

Задачи 91 — 100.Для двухопорной балки, нагруженной, как показано на рис. 35, силами F₁,F₂ и парой сил с моментом М, определить реакции опор, построить эпюры поперечных сил, изгибающих моментов и подобрать необходимый размер поперечного сечения (двутавр или два швеллера), приняв [σ] = 160 МПа. Числовые значения величин для своего варианта задачи взять из таблицы 5.

Задача 101.Плоская стальная пружина (рис. 36, схема I) с размерами поперечного сечения h = 3 мм и Ь = 20 мм прижимает деталь А с силой F = 100 Н. Определить стрелу прогиба f и наибольшие напряжения в поперечном сечении пружины.

Задача 102.Плоская пружина должна быть изготовлена из стальной полосы толщиной δ = 2 мм (рис. 35, схема П). Определить требуемую ширину b, полосы из условия, что жесткость пружины F:f = 16 Н/мм. Принять Е = 2*10(5) мПа.

Задача 103.Проверить жесткость стальной балки (рис. 36, схема III),

если прогиб среднего сечения не должен превышать 1/800 расстояния между опорами.

Задача 104.Определить из условия жесткости стальной балки (рис. 36, схема IV) допускаемое значение нагрузки F. Принять [f] = l/600. При нагрузке, равной допускаемой, определить наибольшие нормальные напряжения в поперечном сечении балки.

Задача 105.Определить ширину b стальной полосы толщиной δ (рис. 36, схема V) из условия, чтобы стрела прогиба была равна 2 мм. При найденном значении b проверить прочность полосы, если [σ] = 160 МПа.

Задача 106.Проверить жесткость стальной балки (рис. 36, схема VI), если [f] == 10 мм, Е = 2*10(5) МПа. Определить максимальные напряжения в поперечном сечении балки. Оценить получившийся результат.

Задача 107.Из расчета на жесткость стальной балки (рис. 36, схема VII) определить допускаемую величину нагрузки F, если [f] = l/700. При найденном значении нагрузки определить максимальные напряжения в поперечном сечении.

Задача 108.Из расчета на жесткость определить требуемые размеры поперечного сечения стальной трубы (рис. 36, схема VIII), работающей на изгиб. Принять [f] = l/800; d₀ = 0,8d.

Задача 109.Из расчета на жесткость стальной балки (рис. 36, схема IX) подобрать требуемый номер двутавра, если [f]= l/600.

Задача 110.Деревянная балка (рис. 36, схема X) шарнирно закреплена по концам и нагружена посередине силой F. Определить допускаемое значение этой силы, если прогиб в середине пролета не должен превышать 12 мм.

Задачи 111—120.Для стального вала постоянного поперечного сечения с двумя зубчатыми колесами (рис. 37), передающего мощность Р, кВт при угловой скорости ω, рад/с (числовые значения этих величин для своего варианта взять из табл. 6): а) определить вертикальные и горизонтальные составляющие реакций подшипников; б) построить эпюру крутящих моментов; в) построить эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях; г) определить диаметр d вала, приняв [σ] = 60 МПа (в задачах 111,113, 115, 117, 119) или [σ]=70МПа (в задачах 112, 114, 116, 118, 120) и полагая F_r₁ = 0,4F_1, F_r₂ = 0,4F₂. В задачах 111—115 расчет производить по гипотезе потенциальной энергии формоизменения, а в задачах 116—120 —по гипотезе наибольших касательных напряжений.

ЗАДАНИЕ ТРЕТЬЕ

Программа

Раздел III. ДЕТАЛИ МАШИН

Тема 28. Основные положения.Цели и задачи третьего раздела предмета «Детали машин» — связь с другими общетехническими и специальными предметами.

Механизм и машина. Классификация машин. Детали машин и их классификация.

Современные тенденции в развитии машиностроения. Ведущая роль Машиностроения среди других отраслей народного хозяйства. Основные задачи дальнейшего развития отечественного машиностроения. Требования, предъявляемые к машинам и их деталям.

Основные условия, определяющие рациональность конструкции машины и ее узлов.

Государственный стандарт (ГОСТ) как основной документ, устанавливающий единые технические требования к промышленной продукции. Роль стандартизации в повышении и развитии научно-технического прогресса. Экономическая эффективность стандартизации. Связь между работой конструктора, технолога и металлурга.

Основные понятия о надежности машин и их деталей. Коэффициент надежности, интенсивность отказов.

Основные критерии работоспособности и расчета деталей машин на прочность, жесткость, износостойкость, теплостойкость, виброустойчивость. Проектные и проверочные расчеты.

МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ

Тема 29. Общие сведения о передачах. Вращательное движение и его роль 1 механизмах и машинах. Назначение передач в машинах. Принципы работы i классификация передач. Основные кинетические и силовые соотношения для механических передач.

Тема 30. Фрикционные передачи.Фрикционные передачи, принцип работы i устройство передач с условно постоянным передаточным отношением. Достоинства и недостатки' фрикционных передач, область их применения. Цилиндрическая передача гладкими катками, определение требуемого усилия нажатия. Понятие о критериях работоспособности. Понятие о конической фрикционной передаче. Кинематические схемы вариантов. Определение диапазона регулирования.

Тема 31. Зубчатые передачи. Общие сведения о зубчатых передачах: достоинства и недостатки, область применения. Классификация зубчатых передач.

Основы теории зубчатого зацепления. Зацепление двух эвольвентных зубчатых колес; основные элементы и характеристики зацепления, взаимодействие зубьев. Зацепление эвольвентного зубчатого колеса с рейкой. Принципиальные основы нарезания зубьев методом обкатки. Делительная окружность. Исходили контур зубчатой рейки. Стандартные параметры зубчатого зацепления без перемещения. Основные понятия о зубчатых колесах со смещением.

Краткие сведения об изготовлении зубчатых колес. Материалы и конструк-1ии зубчатых колес. Виды повреждения зубьев и критерии работоспособности (зубчатых передач.

Прямозубые цилиндрические передачи. Основные геометрические соотношения. Силы, действующие в зацеплении. Расчет зубьев на контактную прочность i изгиб, исходные положения расчета, расчетная нагрузка, формулы проверочного и проектного расчетов. Выбор основных параметров, расчетных коэффициентов и допускаемых напряжений.

Косозубые и шевронные цилиндрические передачи. Основные геометричеcкие соотношения. Силы, действующие в зацеплении. Особенности расчета непрямозубых передач на контактную прочность и изгиб. Основные параметры 1 расчетные коэффициенты.

Прямозубые конические передачи. Основные геометрические соотношения. Силы, действующие в зацеплении. Особенности расчета конических передач на контактную прочность и изгиб. Основные параметры и расчетные коэффициентты. Краткие сведения о конических передачах с криволинейными зубьями.

Тема 32. Передача винт — гайка. Винтовая линия и винтовая поверхность, образование. Профили резьб и основные элементы винтовой пары. Основные типы резьб, их стандартизация, сравнительные характеристики и области применения.

Винтовая передача: достоинства и недостатки, область применения. Силовые соотношения в винтовой паре. Момент в резьбе и момент торцевого трения. Выигрыш в силе. КПД винтовой пары и КПД винтового механизма. Материалы и конструкция деталей передачи. Расчет передачи на износостойкость

и проверка винта на прочность и устойчивость. Выбор основных параметров и расчетных коэффициентов.

Тема 33. Червячные передачи. Общие сведения о червячных передачах: достоинства и недостатки, область применения; материалы червяков и червячных колес.

Червячная передача с Архимедовым червяком, основные геометрические и кинематические соотношения. Понятие о червячных передачах со смещением. Конструктивные элементы передачи. Силы, действующие в зацеплении. КПД передачи. Расчет зубьев на контактную прочность и изгиб; формулы проверочного и проектного расчетов. Тепловой расчет червячной передачи. Выбор основных параметров, расчетных коэффициентов и допускаемых напряжений.

Тема 34. Планетарные и волновые зубчатые передачи. Планетарные передачи, их устройство и области применения. Достоинства и недостатки. Определение передаточных отношений для планетарных передач (метод Виллиса).

Волновые зубчатые передачи, их устройство. Достоинства и недостатки волновых передач. Кинематика волновых передач. Основные конструктивные элементы волновых передач.

Тема 35. Ременные передачи. Общие сведения о ременных передачах: устройство, достоинство и недостатки, область применения. Классификация ременных передач.

Детали ременных передач: приводные ремни, натяжные устройства, шкивы. Сравнительная характеристика плоскоременной и клиноременной передачи. Усилия и напряжения в ремнях. Скольжение ремня на шкивах. Основные геометрические и кинематические соотношения в открытой передаче. Расчет плоскости клиноременных передач по тяговой способности. Долговечность ремней. Выбор основных параметров и расчетных коэффициентов. Краткие сведения о передачах поликлиновыми и зубчатыми ремнями.

Тема 36. Цепные передачи. Общие сведения о цепных передачах: устройства, достоинства и недостатки, область применения. Приводные цепи и звездочки. Критерии работоспособности цепных передач. Подбор цепей и их проверочный расчет. Основные параметры цепных передач.

Контрольная по сопромату (шифр 937)

Один конец стального вертикального бруса жестко защемлен, другой – свободен. Общая длина бруса L (рис.1.1). Одна часть бруса, длина которой l, имеет постоянную по длине площадь поперечного сечения А₁, другая часть – постоянную площадь А₂. В сечении, отстоящем от свободного конца бруса на расстоянии с, действует сила F. Вес единицы материала γ = 78 кН/м 3 , модуль упругости материала Е = 2·10 5 МПа.

2. Составить для каждого участка бруса в сечении с текущей координатой z(0 ≤ z ≤ L) аналитические выражения изменения продольного усилия N_z и нормального напряжения σ_z с учетом собственного веса бруса;

3. Построить эпюры продольных усилий N_z и напряжений σ_z;

Исходные данные: схема 1, L = 5 м, c = 3 м, L/l = 0,2, A₁ = 80·10 -4 м 2 , A₂ = 120·10 -4 м 2 , F = 1,2 кН.

Задача 2

Поперечное сечение бруса состоит из швеллера и равнобокого уголка, соединенных в одно целое. Требуется:

1. Вычертить схему сечения в масштабе 1:2 , на которой указать положение всех осей и все размеры;

4. Определить осевые и центробежный момент моменты инерции сечения относительно осей, проходящих через центр тяжести параллельно полкам;

5. Определить положение главных центральных осей, значения главных центральных моментов инерции, главных радиусов инерции и проверить правильность вычисления моментов инерции.

Исходные данные: схема №3, I – швеллер № 16, II – равнобокий уголок 125 х 125 х 10мм.

Задача №3

Стальной валик (рис.3.1) закручивается двумя парами сил, действующими в двух крайних сечениях. Момент каждой пары сил – М.

2. Определить моменты сопротивления при кручении для сечения I, II, III и по наиболее опасному сечению найти допускаемую величину момента М;

Модуль упругости при сдвиге для материала валика G = 8·10 4 МПа.

Примечание. Сечение III можно приближенно считать квадратным со стороной 0,8 D, т.к. срезы углов весьма незначительны.

Исходные данные: D = 70·10 -3 м, d/D = 0,5, a = 70·10 -2 м, с = 100·10 -2 м, R_cp = 95 МПа.

Задача №4

Для схем балок I, II и рамы III (рис.4.1, рис.4.2, рис.4.3) требуется:

3. Для всех схем составить аналитические выражения изменения изгибающего момента М_х и поперечной силы Q_y, а для схемы III и продольной силы N_z на всех участках;

4. Для всех схем построить эпюры изгибающих моментов М_х и поперечных сил Q_y, а для схемы III – эпюру продольных сил N_z;

5. Руководствуясь эпюрой изгибающих моментов, показать для схем I и II приблизительный вид изогнутых осей балок.

а) для схемы I – прямоугольное hxb при расчетном сопротивлении R_u = 16 МПа (клееная древесина); h/b = 1,5;

б) для схемы II – двутавровое (ГОСТ 8239-72) при расчетном сопротивлении R_u = 200 МПа (сталь).

Исходные данные: с/а = 1,8, P/qa = 0,8, m/qa 2 = 0,4, a= 2,5 м, q = 8 кН/м.

Задача №5

Для схем стальных балок I и II (рис. 5.1) требуется определить методом начальных параметров углы поворота сечений и прогибы в точке В. Модуль упругости Е = 2·10 5 МПа. Поперечные сечения балок: схема I – трубчатое с внешним диаметром D и внутренним – d; схема II – двутавровое.

Задача №6

Пространственный консольный брус с ломаным очертанием осевой линии нагружен сосредоточенной силой F = 1 кН или равномерно распределенной нагрузкой q = 1 кН/м. Вертикальные элементы бруса имеют круглое поперечное сечение диаметром d, горизонтальные элементы – прямоугольное сечение (bxc). Ширина сечения b = d + 20 мм, а высота сечения с = 0,5 b. Размеры бруса, его поперечных сечений и внешняя нагрузка показаны на рис. 6.1.

2. Указать вид сопротивления для каждого участка бруса.

3. Определить на каждом участке нормальные напряжения от совокупности внутренних усилий N_z, M_x, M_y и касательные напряжения от крутящего момента M_z (напряжениями от Q_x и Q_y можно прнебречь).

Исходные данные: d = 60·10 -3 м, а = 1,6 м, схема №7, b =80 мм, с = 40 мм.

Задача №7

ПРОДОЛЬНЫЙ ИЗГИБ СТЕРЖНЕЙ

Для стойки двутаврового поперечного сечения (ГОСТ 8239-72), одинаково закрепленной в обеих плоскостях потери устойчивости и центрально сжатой силой F требуется по заданной схеме (рис.7.1), требуется:

1. Определить грузоподъемность F указать положительные и отрицательные стороны конструкции колонны из двутавра.

2. Для найденной грузоподъемности F, в целях лучшего использования материала, заменить двутавр более рациональным сечением из двух двутавров или двух швеллеров, соединенных планками при сварке (рис.7.2), подобрать для нового варианта сечение, сравнить его по площади с первоначальным и вычертить в масштабе с указанием числовых размеров. Расчетное сопротивление материала R = 160 МПа.

Читайте также: