Формула требуемого момента сопротивления стальной балки
Перед началом расчета стальной балки необходимо собрать нагрузку, действующая на металлическую балку. В зависимости от продолжительности действия нагрузки разделяют на постоянные и временные.
К постоянным нагрузкам относятся:
- собственный вес металлической балки;
- собственный вес перекрытия и т.д.;
К временным нагрузкам относятся:
- длительная нагрузка (полезная нагрузка, принимается в зависимости от назначения здания);
- кратковременная нагрузка (снеговая нагрузка, принимается в зависимости от географического расположения здания);
- особая нагрузка (сейсмическая, взрывная и т.д. В рамках данного калькулятора не учитывается);
Нагрузки на балку разделяют на два типа: расчетные и нормативные. Расчетные нагрузки применяются для расчета балки на прочность и устойчивость (1 предельное состояние). Нормативные нагрузки устанавливаются нормами и применяется для расчета балки на прогиб (2 предельное состояние). Расчетные нагрузки определяют умножением нормативной нагрузки на коэффициент нагрузки по надежности. В рамках данного калькулятора расчетная нагрузка применяется при определении прогиба балки в запас.
Нагрузки можно собрать на нашем сайте.
После того как собрали поверхностную нагрузку на перекрытие, измеряемой в кг/м2, необходимо посчитать сколько из этой поверхностной нагрузки на себя берет балка. Для этого надо поверхностную нагрузку умножить на шаг балок(так называемая грузовая полоса).
Например: Мы посчитали, что суммарная нагрузка получилась Qповерхн.= 500кг/м2, а шаг балок 2,5м. Тогда распределенная нагрузка на металлическую балку будет: Qраспр.= 500кг/м2 * 2,5м = 1250кг/м. Эта нагрузка вносится в калькулятор
2. Построение эпюр
Далее производится построение эпюры моментов, поперечной силы. Эпюра зависит от схемы нагружения балки, вида опирания балки. Строится эпюра по правилам строительной механики. Для наиболее частоиспользуемых схем нагружения и опирания существуют готовые таблицы с выведенными формулами эпюр и прогибов.
3. Расчет по прочности и прогибу
После построения эпюр производится расчет по прочности (1 предельное состояние) и прогибу (2 предельное состояние). Для того, чтобы подобрать балку по прочности, необходимо найти требуемый момент инерции Wтр и из таблицы сортамента выбрать подходящий металлопрофиль. Вертикальный предельный прогиб fult принимается по таблице 19 из СНиП 2.01.07-85* (Нагрузки и воздействия). Пункт2.а в зависимости от пролета. Например предельный прогиб fult=L/200 при пролете L=6м. означает, что калькулятор подберет сечение прокатного профиля (двутавра, швеллера или двух швеллеров в коробку), предельный прогиб которого не будет превышать fult=6м/200=0,03м=30мм. Для подбора металлопрофиля по прогибу находят требуемый момент инерции Iтр, который получен из формулы нахождения предельного прогиба. И также из таблицы сортамента подбирают подходящий металлопрофиль.
4. Подбор металлической балки из таблицы сортамента
Из двух результатов подбора (1 и 2 предельное состояние) выбирается металлопрофиль с большим номером сечения.
Формулы для расчетов на изгиб
Подборка формул для расчета балок и рам на изгиб и решения задач сопротивления материалов по расчету внутренних сил, напряжений, деформаций и перемещений при изгибе.
σ — нормальные напряжения,
τ — касательные напряжения,
Qy – внутренняя поперечная сила,
Mx – внутренний изгибающий момент,
Ix – осевой момент инерции сечения балки,
Wx – осевой момент сопротивления сечения,
A — площадь поперечного сечения,
[ σ ], [ τ ] – соответствующие допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
y — расстояние от оси x до рассматриваемой точки сечения балки.
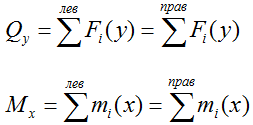
Формула кривизны балки в заданном сечении
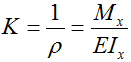
Расчет нормальных напряжений в произвольной точке сечения балки при изгибе
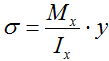
Условие прочности по нормальным напряжениям при изгибе (проверочный расчет)
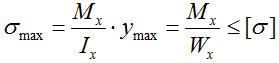
Осевые моменты инерции I и сопротивления W
Касательные напряжения в произвольной точке сечения при изгибе определяются по формуле Журавского:
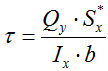
Sx * — статический момент относительно оси x отсеченной части сечения
b — ширина сечения на уровне рассматриваемой точки
Условие прочности балки по касательным напряжениям
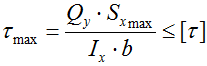
Дифференциальное уравнение линии изогнутой оси балки
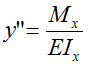
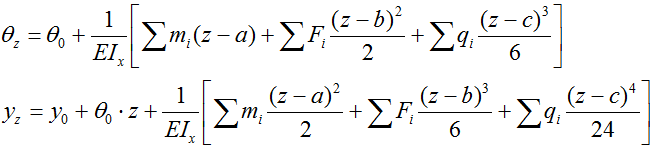
θ z, yz — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,
θ 0, y0 — соответственно угол наклона и прогиб сечения балки в начале координат,
m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,
a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,
c — расстояние от начала координат до начала распределенной нагрузки q.
Расчет балки
При расчете стальных балок необходимо руководствоваться СП 16.13330 «Стальные конструкции».
В данном обзоре я рассмотрю расчет балок 1-го класса напряженно-деформированного состояния (напряжения по всей площади напряжения не превышают расчетного сопротивления стали). Расчёт подкрановых, бистальных, защемленных и многопролетных балок будет рассмотрен отдельно.
Элементы конструкции должны иметь запас прочности по 1-му и 2-му предельному состоянию.
По 1-му предельному состоянию проверяется прочность элементов. Нагрузки для расчета по 1-му предельному состоянию выше, чем по 2-му предельному состоянию т.к. используются коэффициенты запаса для нагрузок.
По 2-му предельному состоянию проверяются деформации конструкции.
Расчеты по 1-му предельному состоянию:
- Расчет на прочность при действии изгибающего момента
- Расчет на прочность при действии поперечной силы
- Расчет на прочность стенки балки при действии сосредоточенной силы
- Расчет на прочность в опорном сечении
- Расчет на общую устойчивость
- Расчет на устойчивость стенок и поясных листов балки
Расчеты по 2-му предельному состоянию:
1. Расчет на прочность при действии изгибающего момента
В первую очередь необходимо подобрать балку по изгибающему моменту.
Прочность стальной балки на изгиб проверяется по следующей формуле (п.8.2.1 СП 16.13330.2011 или 5.12 СНиП II-23-81*):
где M – максимальный момент, возникающий в балке (находится по эпюре моментов);
Wn,min – момент сопротивления сечения (находится по таблице или вычисляется для данного профиля), у сечения обычно 2-а момента сопротивления сечения, в расчетах используется Wx если нагрузка перпендикулярна оси х-х профиля или Wy если нагрузка перпендикулярна оси y-y;
Ry – расчетное сопротивление стали при изгибе (задается в соответствии с выбором стали);
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП 16.13330.2011 Стальные конструкции либо таблице 6* СНиП II-23-81) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Из этой формулы можно вычислить минимально требуемый момент сопротивления сечения.
Вначале вычисляем максимальный момент от нагрузок. На этом этапе мы еще не знаем массу балки и ее можно не учитывать при предварительном расчете.
Далее выбираем марку стали. При выборе марки стали необходимо учитывать класс конструкции и климатические условия эксплуатации – если конструкция эксплуатируется в холодном климате в неотапливаемом здании, то марка стали не должна быть хрупкой. Прочность стали выбирается исходя из экономического расчета – несмотря на то, что с увеличением марки стали ее стоимость увеличивается, сечение балки из более прочной стали может быть меньше и соответственно будут меньше нагрузки. Для того, чтобы выбрать оптимальную марку стали необходимо сделать несколько расчетов и оценить их.
После того, как мы предварительно рассчитали минимальный момент сопротивления сечения (Wn) подбираем из сортамента профиль, имеющий W не много выше чем требуемый и имеющий наименьшую массу. Для балок оптимальным профилем является двутавр, швеллер. Возможно использование составного сечения из листов. При расчете важно правильно учесть положение профиля – Wx используется, если ось x-x перпендикулярна направлению приложения нагрузки. Соответственно профиль необходимо располагать так, чтобы момент сопротивления сечения был максимальным (от того как расположить профиль многое зависит).
После выбора сечения необходимо прибавить к изгибающему моменту момент, создаваемый массой балки и вновь проверить сечение.
Если балка расположена под углом, то расчет прочности при изгибе производят по следующей формуле:
где требуется разложить силу на направляющие по оси х-х и у-у и отдельно вычислить максимальные моменты Mx и My вокруг оси х-х и у-у соответственно.
В СП 16.13330.2011 дополнительно требуют учитывать бимомент, формула выглядит следующим образом:
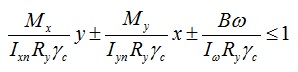
x и y — расстояния от главных осей до рассматриваемой точки;
Ixn,Iyn — моменты инерции сечения, находятся по таблице согласно ГОСТ-у на выбранный профиль;
Iω — секториальный момент инерции сечения, можно найти в приложении 3 руководства по подбору сечений стальных конструкций;
ω — секториальная площадь.
Здесь рассматриваются несколько точек, как правило 4 крайние точки профиля и для них проверяют условия, знаки подбирают согласно эпюрам напряжения. Подробно расчет профилей с учетом бимомента расписано в книге Д.В.Бычкова Строительная механика стержневых тонкостенных конструкций.
Для прогонов наклонной кровли из швеллера для упрощения расчета бимомент можно не учитывать т.к. он разгружает профиль на 10-15%, и это будет запасом прочности. В других случаях рекомендуется принимать конструктивные меры препятствующие возникновению закручивающего момента.
2. Расчет на прочность при действии поперечной силы
Далее необходимо проверить профиль на действие касательных (поперечных) сил по формуле:
где Q – наибольшая поперечная сила (можно определить согласно эпюре Q), для балки наибольшее значение получается на опорах;
S – статический момент сдвигаемой части сечения (определяется по таблице для выбранного профиля);
I – момент инерции сечения (определяется по таблице для выбранного профиля);
tw – толщина стенки балки;
Rs — расчетное сопротивление стали сдвигу, равно 0,58 от Ry согласно Таблице 2 СП 16.13330.2011;
γc – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП Стальные конструкции) для балок сплошного сечения коэффициент равен 0,9, при расчете по сечению, ослабленному отверстиями 1,1.
Если профиль не удовлетворяет условию, то необходимо увеличить сечение.
3. Расчет на прочность стенки балки при действии сосредоточенной силы
Расчет на прочность стенки балки, не укрепленной ребрами жесткости, при действии сосредоточенной силы и в опорных сечениях определяют по формуле:
здесь F – расчетное значение нагрузки;
lef – условная длина распределения нагрузки;
tw – толщина стенки балки.
Условную длину распределения нагрузки можно определить по формуле
для следующих случаев:
для прокатной балки:
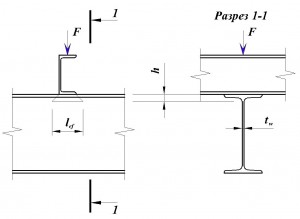
где b – ширина полки швеллера
h – сумма толщины верхней полки и радиуса закругления
для сварной балки:
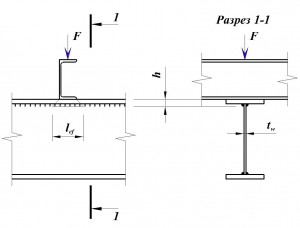
где h – сумма толщины верхней полки и катета сварного шва.
4. Расчет на прочность в опорном сечении
Расчет на прочность в опорном сечении балки (при Mx=0 и My=0) следует определять по формулам:
где Aw– площадь сечения стенки,
Af– площадь сечения полки,
Rs–расчетное сопротивление стали сдвигу.
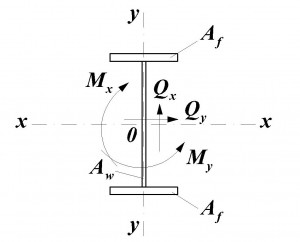
При ослаблении стенки отверстиями для болтов левую часть формулы необходимо умножить на коэффициент α, который находиться по формуле:
где s – шаг отверстий в одном ряду;
d – диаметр отверстия.
Расчет на прочность для защемленных и неразрезных балок мы рассмотрим отдельно.
5. Расчет на общую устойчивость
Далее необходимо проверить балку на устойчивость.
Данный расчет можно не выполнять:
а) при передаче нагрузки через сплошной жесткий настил (плиты железобетонные, плоский или профилированный металлический настил, волнистая сталь и т.п.), непрерывно опирающийся на сжатый пояс балки и надежно с ним связанный (с помощью сварки, болтов, самонарезающих винтов), при этом силы трения учитывать не стоит;
б) если условная гибкость сжатого пояса балки меньше предельных значений. Условная гибкость вычисляется по формуле:
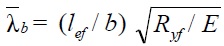
Предельное значение гибкости пояса вычисляется по формулам:
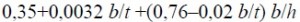
при приложении нагрузке к верхнему поясу
при приложении нагрузке к нижнему поясу
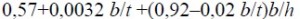
независимо от уровня приложения нагрузки при расчете участка балки между связями или при чистом изгибе
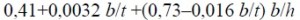
где b – ширина сжатого пояса;
t – толщина сжатого пояса;
h – расстояние (высота) между осями поясных листов.
- Значения предельной гибкости определены при 1≤ h/b ≤6 и 15≤ b/t ≤35; для балок с отношением b/t
- Для балок с фрикционными поясными соединениями предельную гибкость следует умножать на 1,2
Проверка общей устойчивости при изгибе в плоскости стенки, совпадающей с плоскостью симметрии сечения, осуществляется по следующей формуле:
если изгиб происходит в 2-х плоскостях (и наличии секториальных напряжений), тогда проверку осуществляют по формуле:
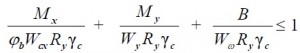
где φb – коэффициент устойчивости при изгибе, подробный расчет коэффициента устойчивости (φb) приведен в приложении Ж СП 16.13330.2011 Стальные конструкции;
Wcx – момент сопротивления сечения относительно оси x-x, вычисленного для сжатого пояса;
Wy – момент сопротивления сечения относительно оси y-y, совпадающий с плоскостью изгиба;
Wω – секторальный момент сопротивления сечения.
При расчете значения φbза расчетную длину балки lef следует принимать расстояние между точками закрепления сжатого пояса от поперечных смещений. При отсутствии связей lef=l (где l – пролет балки).
Если в процессе расчета выясняется, что общая устойчивость балки не обеспечивается, то следует уменьшить расчетную длину сжатого пояса, изменив систему связей.
6. Расчет устойчивости стенок и поясных листов балки
Устойчивость стенок балок 1-го класса следует считать обеспеченной если условная гибкость стенки, вычисленная по формуле:
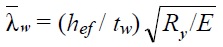
hef — расчетная высота стенки, принимаемая согласно требованиям 7.3.1 СП 16.13330.2011;
tw — толщина стенки балки;
Ry — расчетно сопротивление стали при изгибе;
E — модуль упругости стали равный 210 ГПа (210 000 МПа)
Условная гибкость стенки не должна превышать значений:
3,5 – при отсутствии местного напряжения в балках с двухсторонними поясными швами;
3,2 – при отсутствии местного напряжения в балках с односторонними поясными швами;
2,5 – при наличии местного напряжения в балках с двухсторонними поясными швами.
Если условная гибкость стенки выше требуемой, то стенки необходимо усилить ребрами жесткости и сделать проверку согласно п. 8.5.3 СП 16.13330.2011.
7. Расчет прогиба балки
Расчет на 2-е предельное состояние балки заключается в расчете максимального прогиба.
Высокие деформации могут привезти к нарушению герметичности, невозможности эксплуатации, плохому эстетическому восприятию конструкции, поэтому конструкция не должна сильно деформироваться. Предельные прогибы конструкций приведены в приложении Е СП 20.13330 Нагрузки и воздействия
К примеру, для балки покрытия, длиной 6 м, предельный прогиб составляет 1/200 длины пролета т.е. 30 мм.
Формула определения прогиба зависит от способа приложения нагрузки, например однопролетной шарнирно-закрепленной с равномерно-распределенной нагрузкой прогиб рассчитывается по формуле:
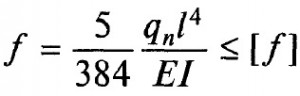
где q – равномерно-распределенная нагрузка, выраженная в кг/м (Н/м);
l – длина балки в метрах;
E – модуль упругости (для стали равен 200-210 ГПа);
I – момент инерции сечения.
Для других способов нагрузки балки формулы смотрите в справочниках по сопротивлению материалов.
Если расчетный прогиб больше допускаемого, то следует увеличить сечение балки.
Как найти расчетный момент и поперечную силу читайте в статье Построение эпюр балки
Как правильно закрепить балку на колонне читайте в статье Опорные узлы балки
Как рассчитать балку в SCAD и подобрать сечение читайте в статье Расчет балки в SCAD
Полный расчет балки на прочность и жесткость
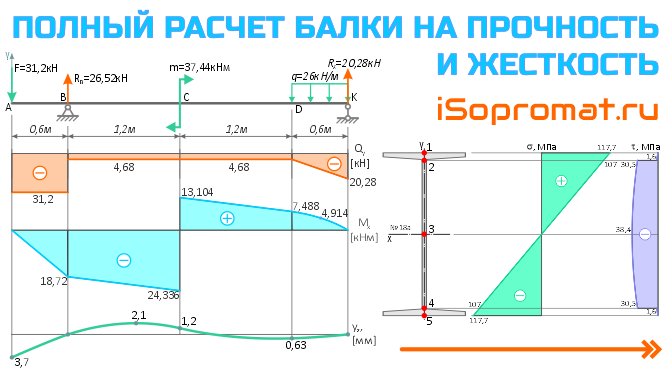
Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки при заданной системе внешних изгибающих нагрузок.
Задача
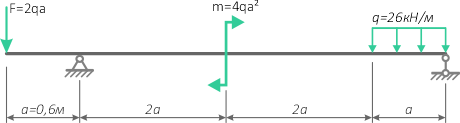
Выполнить полный расчёт на прочность и проверить жёсткость стальной, двутавровой, статически определимой балки на двух опорах
при следующих данных:
Интенсивность равномерно распределенной нагрузки q=26кН/м, продольный размер a=0,6м, сосредоточенная сила F=2qa, изгибающий момент m=4qa 2 .
Допускаемые нормальные напряжения [σ]=160МПа,
Модуль упругости I рода Е=200ГПа.
Допустимый прогиб балки [f]=l/400.
Последовательность решения задачи
Для расчета балки на прочность
- Вычерчивается схема нагружения в масштабе, с указанием числовых значений приложенных нагрузок;
- Строятся эпюры внутренних силовых факторов Qy и Mx;
- По условию прочности подбирается двутавровое сечение (№ двутавра) стальной балки:
- Для балки двутаврового профиля выполняется полная проверка на прочность, приняв
- Проверяется прочность по главным напряжениям в опасных точках сечения по III гипотезе прочности
- По результатам расчетов дается заключение о прочности балки при выбранном сечении.
- В случае невыполнения условия прочности по главным напряжениям, подбирается новый номер двутавра.
Для расчета балки на жесткость
- С использованием универсальных уравнений метода начальных параметров (МНП) определяются углы поворота θ над опорами и прогибы в характерных сечениях (2-3 сечения), а также, максимальные прогибы балки в пролете и консольной части;
- По этим данным, в соответствии с эпюрой Mx, строится линия изогнутой оси балки;
- Проверяется выполнение условия жесткости балки.
- Если условие жесткости не удовлетворяется, подбирается новое двутавровое сечение, обеспечивающее необходимую жесткость.
Решение
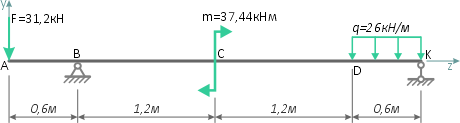
Рассчитаем численные значения силы F и момента m, которые были заданы в виде переменных.
Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.
Показываем оси системы координат y-z и обозначаем характерные сечения балки.
Полный расчет стальной балки на прочность
Определение реакций в шарнирных опорах балки
Направим реакции опор вверх и запишем суммы моментов относительно точек на опорах, нагрузок приложенных к балке
Из составленных уравнений выражаем и находим реакции.
Из первого уравнения
из второго
Положительные значения указывают на то, что произвольно заданное направление реакций вверх оказалось верным.
Выполним проверку найденных реакций опор спроецировав все силы на ось y
Равенство суммы проекций сил нулю говорит о том что реакции опор определены правильно.
Более подробно, пример определения опорных реакций для балки рассмотрен здесь
А также в нашем коротком видеоуроке:
Построение эпюр внутренних силовых факторов
Рассчитаем значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.
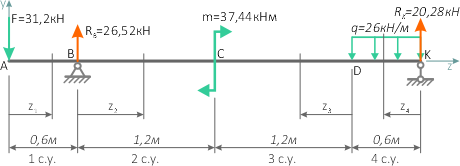
Балка имеет 4 силовых участка.
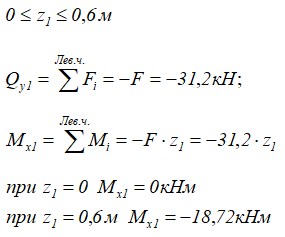
1 участок (AB)
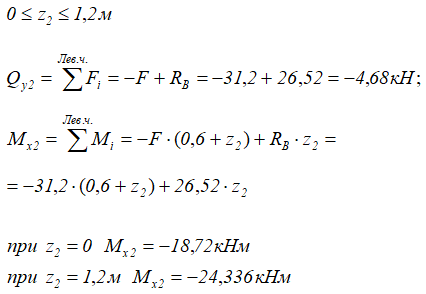
2 участок (BC)
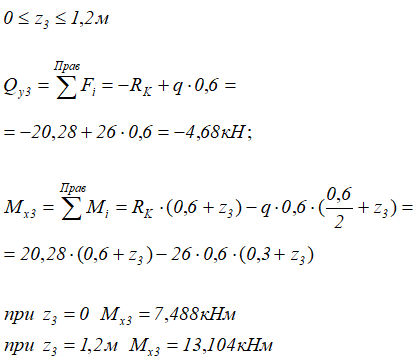
3 участок (CD)
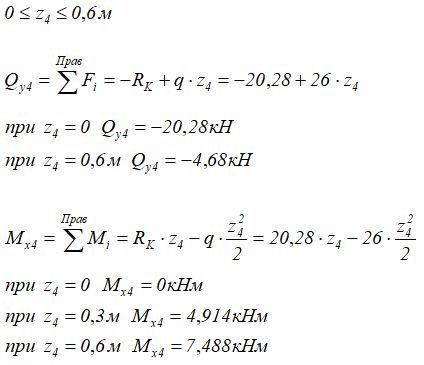
4 участок (DK)
Здесь, значения Qy на границах участка имеют одинаковый знак, поэтому на этом участке, на эпюре Mx экстремума не будет.
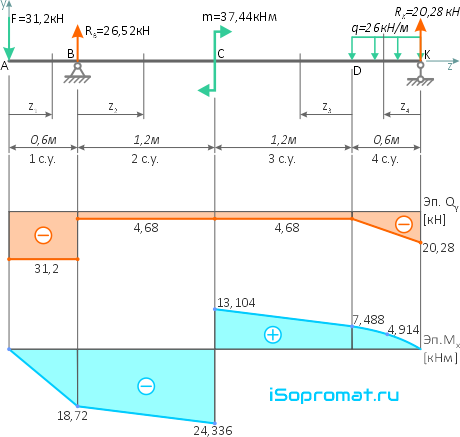
По полученным данным строим эпюры внутренних поперечных сил Qy и изгибающих моментов Mx.
Проверка построенных эпюр:
— по дифференциальным зависимостям
— в сечениях балки, где приложены сосредоточенные силы, на эпюре Qy имеются скачки значений на величину соответствующей силы;
— в сечениях балки, где приложены изгибающие моменты, на эпюре Mx скачки значений на величину соответствующего момента.
Все условия выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасным является сечение балки в точке C, где:
Mx=Mx max=-24,336кНм
Qy=-4,68кН
Подбор двутаврового сечения балки
Подберем двутаврового сечение балки по условию прочности по нормальным напряжениям
где
Mx max – максимальное значение внутреннего изгибающего момента в сечениях балки. Принимается с построенной эпюры Mx;
Wx – осевой момент сопротивления поперечного сечения балки относительно горизонтальной оси x;
[σ] – допустимые нормальные напряжения.
Выразим и рассчитаем минимально необходимое значение осевого момента сопротивления поперечного сечения балки Wx обеспечивающего её прочность по нормальным напряжениям
По сортаменту прокатной стали выбираем номер двутавра имеющий осевой момент сопротивления близкий к расчетному Wx=152,1см 3 в большую сторону.
Это двутавр №18а у которого Wx=159,0см 3 .
Максимальные нормальные напряжения в сеченииЭтот двутавр будет работать при максимальных нормальных напряжениях в крайних слоях опасного сечения балки.
Максимальные нормальные напряжения выбранного номера двутавра не превышают допустимых значений, значит сечение подобрано верно.
Полная проверка на прочность двутаврового сечения
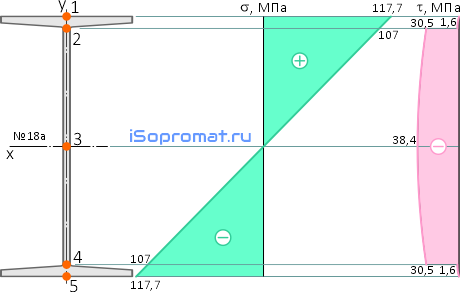
При изгибе тонкостенных прокатных профилей, таких как, например, двутавр или швеллер, в местах соединения стенки с полкой нормальные и касательные напряжения имеют не максимальные, но достаточно большие значения.
Их совместное действие, выраженное в виде главных (эквивалентных) напряжений, может превышать допустимые значения, что будет означать потерю прочности в этих точках поперечного сечения балки.
В отношении главных напряжений неблагоприятным является сечение балки B, в котором максимально значение поперечной силы при значительном изгибающем моменте:
Для полной проверки на прочность построим эпюры нормальных и касательных напряжений в сечении B для выбранного номера двутавра.
Построение эпюр нормальных и касательных напряжений в сечении балки подробно рассмотрено здесь:
Для выполнения расчетов, из сортамента выпишем необходимые геометрические характеристики выбранного номера двутавра:
Высота сечения
h=180мм;
Ширина сечения
b=100мм;
Толщина стенки
d=5,1мм;
Толщина полки
t=8,3мм;
Осевой момент инерции поперечного сечения
Ix=1430см 4 ;
Статический момент сечения
Sx=89,8см 3 .
Двутавровое сечение по высоте имеет 5 характерных точек: верхнюю (1), нижнюю (5), среднюю (3) и две точки в местах перехода стенки в полку двутавра (2 и 4).
Для построения эпюр, определим значения напряжений в указанных точках сечения.
Нормальные напряжения в сечении балки распределяются по линейному закону, поэтому для построения эпюры достаточно найти максимальные значения
Касательные напряжения в характерных точках сечения рассчитываются по формуле Журавского
где
Qy — поперечная сила в данном сечении. Принимается с эпюры с учетом знака;
Ix – осевой момент инерции поперечного сечения;
by – ширина сечения на уровне рассматриваемой точки;
Sx* — статический момент части сечения, расположенной между уровнем рассматриваемой точки и верхним (нижним) краем сечения.
Рассчитаем значения касательных напряжений
Так как выше точки 1 и ниже точки 5 площадь сечения равна нулю, то статический момент Sx* для этих точек тоже равен нулю, следовательно
В точке 3
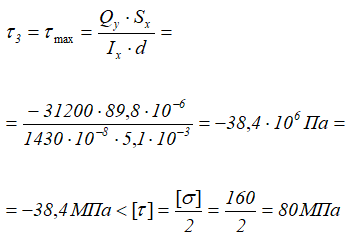
В точке 3 будут максимальные касательные напряжения, т.к. для неё статический момент сечения Sx максимальный при минимальной ширине сечения d
Видно, что прочность сечения по касательным напряжениям обеспечена.
В точках, где стенка двутавра переходит в полку, будут скачки напряжений, так как на уровне этих точек резко меняется ширина сечения
Рассчитаем значения напряжений в этих точках для стенки (с) и полки (п)
Статический момент полки двутавра
Касательные напряжения в точках 2 и 4 полки
Касательные напряжения в точках 2 и 4 стенки
По этим данным строим эпюры нормальных и касательных напряжений для выбранного номера двутавра.
Рассчитаем величину главных напряжений в точках соединения полки со стенкой двутавра (т. 2 и 4)
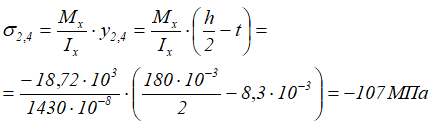
Нормальные напряжения в рассматриваемых точках
Эквивалентные напряжения в опасных точках сечения
Как видно, величина эквивалентных напряжений не превышает допустимых значений, следовательно, выбранный номер двутавра удовлетворяет условию прочности и по главным напряжениям.
Полный расчет балки на жесткость
Для того чтобы балка удовлетворяла условию жесткости, линейные перемещения (прогибы) балки yz не должны превышать заданных допустимых значений [f], т.е. должно выполняться условие жесткостиРасчет перемещений сечений балки
Расчет перемещений сечений балки выполним методом начальных параметров (МНП).
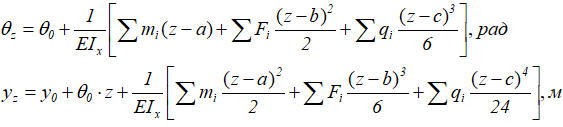
Шаблоны уравнений метода начальных параметров имеют вид:
Здесь:
θz — угловое перемещение (угол наклона) рассматриваемого сечения;
yz — вертикальное линейное перемещение (прогиб) рассматриваемого сечения балки;
z – расстояние от выбранного начала координат балки до рассматриваемого сечения (координата);
θ0, y0 — соответственно угловое и линейное перемещения балки в выбранном начале координат (начальные параметры);
E – модуль упругости I рода для материала балки;
Ix – осевой момент инерции сечения балки;
m, F, q – соответственно моменты, сосредоточенные силы и распределенные нагрузки, приложенные к балке (включая опорные реакции и компенсирующую распределенную нагрузку);
a, b – расстояние от начала координат до соответствующих моментов m и сил F;
c – расстояние от начала координат до сечения балки, где начинается действие распределенной нагрузки q.
Составляем уравнения МНП для заданной балки
Начало координат принимаем в крайнем правом сечении балки, так как оно расположено на опоре.
Распределенная нагрузка не доходит до конца балки, поэтому продляем её действие и на этой же длине добавляем компенсирующую нагрузку той же интенсивности но противоположного направления.
Запишем нагрузки в уравнения МНП последовательно по участкам с учетом знаков
Для определения начальных параметров θ0 и y0 запишем граничные условия.
На опорах прогибы балки равны нулю, т.е.
Из второго граничного условия, используя уравнение прогибов для точки B определим угол поворота сечения в начале координат θ0
Откуда, при z=3м
Для построения линии изогнутой оси балки определим углы наклона сечений балки на опорах θB, θK и прогибы в характерных сечениях yA, yC, yD.
Углы поворота сечений на опорах
Далее, для краткости, сократим дробь перед скобками
Линейные перемещения (прогибы) характерных сечений балки
Прогиб сечения A (yz при z=3,6м)
Прогиб сечения C (yz при z=1,8м)
Прогиб сечения D (yz при z=0,6м)
Расчет максимальных прогибов балки

Экстремумы прогибов балки будут в точках, где угол наклона сечения балки равен нулю.
Для их определения, приравниваем к нулю уравнения углов наклона сечений по каждому участку балки, откуда определяем координаты z экстремумов прогибов на участке (если они есть).
1 участок (KD).
Уравнение решений не имеет (т.е. экстремумов на участке нет), это значит, что максимальный прогиб на этом участке будет на его левой границе (в сечении D), так как правая точка участка расположена на опоре.

2 участок (DC).
То есть, экстремум прогибов на втором участке будет на расстоянии z2=0,782м от начала координат.
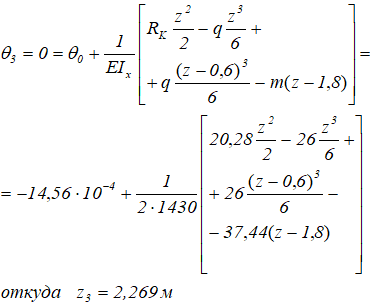
3 участок (CB).
Экстремум прогибов на третьем участке в сечении, на расстоянии z3=2,269м от начала координат.
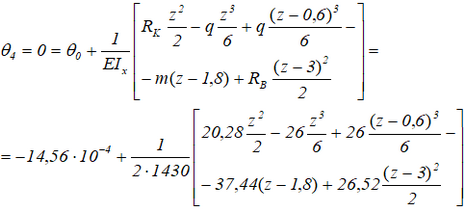
4 участок (BA).
Данное уравнение решений также не имеет, следовательно, максимальный прогиб на конце консоли, так как на правой границе участка – опора.
Значения максимальных прогибов балки на втором и третьем участках определяем из соответствующих уравнений прогибов для найденных значений z.
По полученным данным строим линию изогнутой оси балки в соответствии с эпюрой изгибающих моментов Mx и с указанием углов поворота сечений на опорах.
Проверка балки на жесткость
Проверяем балку на жесткость, сравнивая по модулю максимальные значения прогибов ymax в пролёте и на консольной части с допустимыми [f].
Балка считается жесткой, если прогибы её сечений не превышают допустимых значений, т.е.
Рассчитаем абсолютные значения допустимых прогибов заданной балки:
В пролете
На консольной части
Для проверки на жесткость сравниваем величину рассчитанных ранее максимальных прогибов сечений балки с соответствующими допустимыми значениями.
В пролете
На консоли
Как видно, максимальный прогиб на конце консольной части балки превышает соответствующее допустимое значение, следовательно, балка не удовлетворяет заданному условию жесткости.
Жесткость балки можно увеличить до требуемого значения путем увеличения момента инерции её сечения, т.е. подбором сечения большего размера.
Подберем двутавр другого номера, который будет обеспечивать необходимую жесткость балки.
Определяем, во сколько раз надо уменьшить величину максимального перемещения сечения.
Тогда, расчетный момент инерции нового сечения балки
По сортаменту выбираем двутавр №20 с осевым моментом инерции сечения Ix=1840см 4 .
Для начала требуется пересчитать угол наклона сечения балки в начале координат.
Рассчитываем прогиб сечения A с новым размером сечения
Условие жесткости выполняется.
Таким образом, двутавр №20 обеспечивает необходимую прочность и жёсткость заданной балки.
Полный расчет заданной балки на прочность и жёсткость выполнен.
Расчет балки на прогиб - формулы, параметры и примеры решения
Расчет балки на прогиб нужно проводить практически для любой конструкции, чтобы проверить ее надежность и прочность. Под влиянием внешних, внутренних факторов, природных явлений балка подвержена деформации.
Балку сравнивают со стержнем, закрепленным на опорах. Чем больше опор, тем сложнее провести расчет самостоятельно. Основная нагрузка считается путем сложения сил, перпендикулярно направленных к сечению.
Данный расчет – основы сопромата, помогает определить наивысшую деформацию. Значения показателей должны входить в рамки допустимых величин.
Виды балок
При возведении зданий используется балки разных конфигураций, размеров, профиля, характера сечения. Их изготавливают из металла и дерева. Для любого вида используемого материала нужен индивидуальный расчёт изгиба.
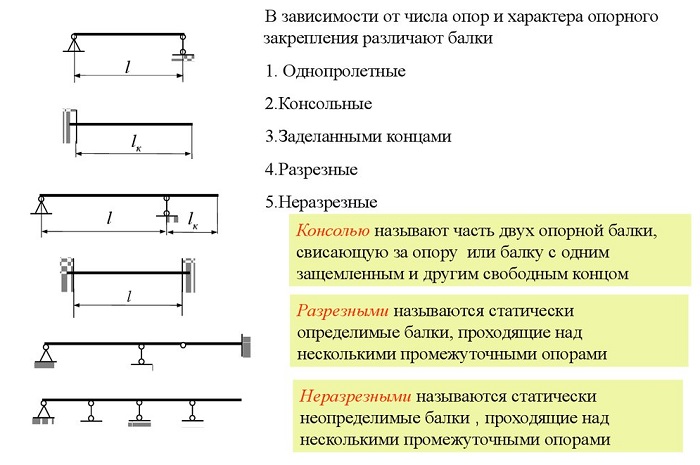
Деревянные - их используют в основном при строительстве индивидуальных построек. Они применяются при возведении полов, потолков, несущих перекрытий. Дерево – капризный материал и подвержено деформации. Для определения максимального изгиба, существенны такие параметры: используемый профиль, размер, нагрузка, характер поперечного сечения.
Металлические - такие балки изготавливают из сплава металлов и сечение у них сложное. Поэтому особое внимание уделяется жесткости, а также прочности соединений. Балки из металла применяются в возведении многоэтажек, сооружений, требующих высокой прочности.
Прочность и жесткость балки
При проектировании следует учесть изгиб балок, чтобы конструкция была надежная, качественная, прочная и практичная.
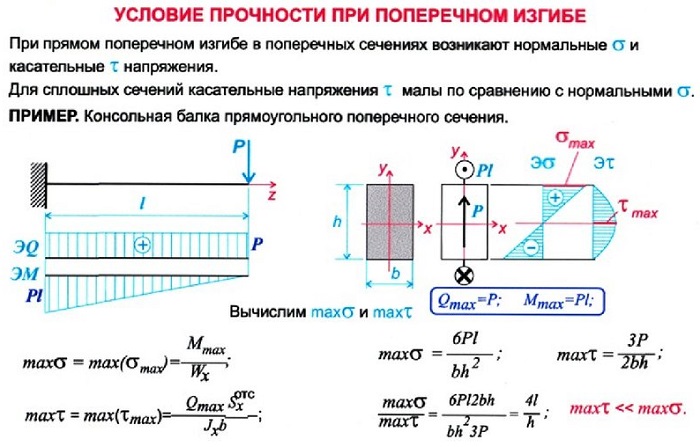
На эти параметры влияют следующие факторы:
величина наружных нагрузок, их положение;
параметры, характер, нахождение поперечного сечения;
число опор, метод их закрепления.
Выделяют 2 метода исчисления: простой – применяется увеличительный коэффициент, и точный – дополнительно включает пограничные подсчеты.
Построение эпюр балки
Эпюра распределения величины нагрузки на объект:
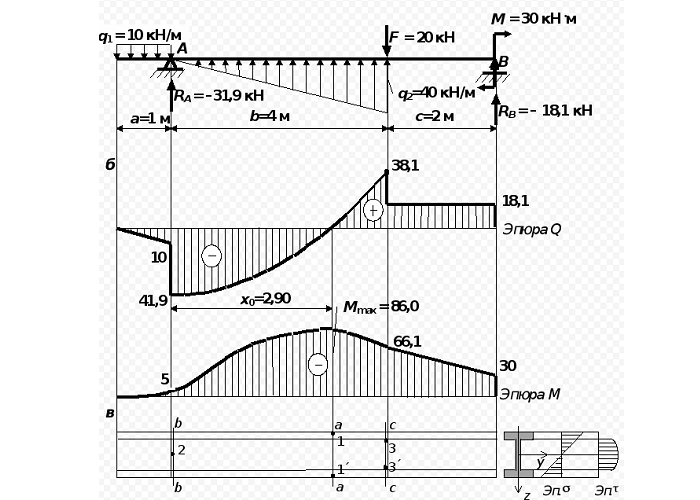
Расчет на жесткость
В формуле обозначены:
M – max момент, возникающий в брусе;
Wn,min – момент сопротивления сечения (табличный показатель);
Ry – сопротивление на изгиб (расчётный показатель);
γc – показатель условий труда (табличный показатель).
Такой расчет не трудоемок, но для более верного значения требуется следующее:
рабочий план объекта;
определение характеристик балки, характер сечения;
определение max нагрузки, воздействующей на брус;
оценка точки max прогиба;
проверка прочности max изгибающего момента.
Расчет моментов инерции и сопротивления сечения
J – момент инерции сечения;
W – момент сопротивления.
Для определения данных параметров необходимо учитывать сечение по грани разреза. Если момент инерции возрастает, величина жесткости также возрастает.
Нахождение максимальной нагрузки и прогиба
Формула для вычисления:
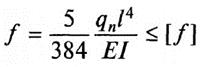
q – нагрузка равномерно-распределенная;
E – гибкость (табличный показатель);
Нагрузки учитываются статические и периодические.
Расчет на прогиб и его особенности
Он необходим для всех перекрытий при высоких эксплуатационных нагрузках.

При применении соответствующих коэффициентов, придерживаются следующего:
балка, держащаяся на одной жесткой и одной шарнирной опоре, подвергающаяся воздействию сосредоточенной нагрузки;
балка, держащаяся на жесткой и шарнирной опоре, подвергающаяся воздействию распределенной нагрузки;
нагрузка консольного типа;
воздействие комплексной нагрузки.
Пример расчет балки на прогиб
Рассмотрим задачу из курса сопромата.
Дано: балка четырехугольного сечения 20 на 30 см; поперечная сила Q = 19 кН; изгибающий момент М = 28 кНм.
Необходимо рассчитать напряжение: нормальное и в пределе К, отдаленной на 11 см от оси, узнать прочность бруса из дерева, при [σ] = 10 МПа, [τ] = 3 МПа.
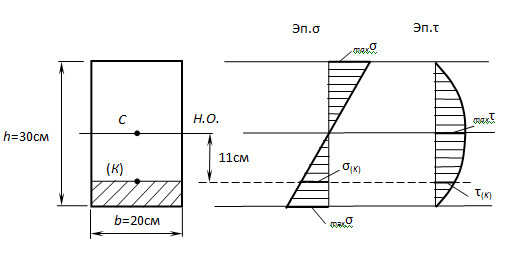
Чтобы узнать σ(К), τ(К), σmax, τmax определяем значение осевого момента инерции общего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсеченного ряда и статического момента середины сечения Smax:
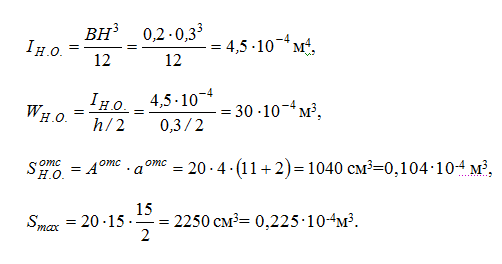
Из этого следует:
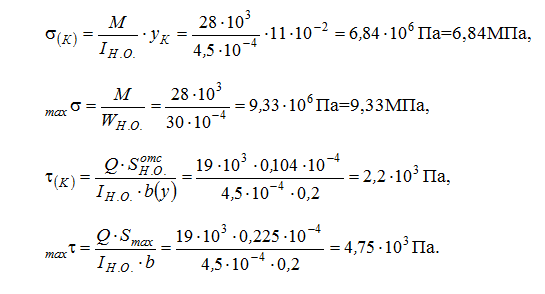
Определение прочности по нормальному напряжению:
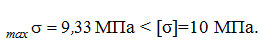
Определение прочности по касательному напряжению:
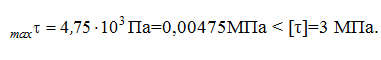
При проектировании конструкций важно соблюдать все физико-механические вычисления на прочность. Удобно и качественно произвести расчеты может онлайн, что существенно сократит временные сроки.
Калькулятор выполняет подробный подсчет на основе формул, эпюр усилий, подбирает номер сечения металлической балки из прокатных профильных, двутавровых материалов, а также из металлических труб.
Читайте также:
