Замена столбца матрицы mathcad
Конструирование выражений в MathCAD осуществляется с помощью математических панелей. Ввод заканчивается клавишей Enter или щелчком мыши вне определения. Синий уголок показывает текущий операнд выражения, он может быть расширен клавишей " Пробел ". В качестве разделителя целой и дробной части числа используется точка.
Арифметические операции , простейшие функции, знаки присваивания переменным (символ :=) можно вводить, используя панель Calculator (Калькулятор). Численные ответы выражений определяются нажатием клавиши [=] на клавиатуре. В качестве элементов выражения могут использоваться функции определенных интегралов, сумм и произведений с панели Calculus.
Для ввода математической функции различной категории используется команда Insert /Function (Вставить функцию).
Для ввода текстового комментария необходимо ввести знак двойной кавычки ", затем вводить текст. Текстовая область, как и любая другая, может быть перемещена на рабочем листе или скопирована в буфер . Маркеры текстовой области позволяют менять её размеры
1.4.1. Переменные и функции.
Переменная в MathCAD – это идентификатор, который используется в выражениях и которому можно присвоить числовое значение. Идентификатор – набор букв и цифр, первым из которых должна быть буква; буквы могут быть латинскими или греческими с соответствующей панели; малые и большие буквы различаются; в качестве цифры может использоваться символ подчеркивания. При выполнении цепочки выражений последовательность вычислений в документе определяется слева - направо и сверху - вниз. Чтобы цепочка выражений была вычислена, надо всем переменным присвоить числовые значения. Присваивания бывают двух видов: локальные и глобальные. Локальное присваивание осуществляется нажатием символа := на панели Калькулятор. Присвоенное значение в документе начинает действовать с момента его записи (слева-напрво и сверху-вниз).
Глобальное присваивание действует в пределах всего документа независимо от места его определения. Глобальное присваивание определяется символом === с панели Evaluation. Ниже (Рис.1.10) приведен пример цепочки выражений с использованием локального (для х) и глобального (для а) присваивания:

, " />
,
, +e^x" />
, ,
Встроенные константы
Символьный процессор распознает и способен выдавать математические константы в качестве результата.
Вычислительный процессор воспринимает как числа

-бесконечность ( клавиши <Ctrl>+<Shift>+<z>);

- основание натурального логарифма (клавиша <е>);

; - число "пи" (вводится клавишами <Ctrl>+<Shift>+<p>);

- мнимая единица (вводится клавишами <1>, <i> или <1>, <j>);

- символ процента, <%>, эквивалентный 0,01.
Основные типы переменных
Действительные числа
Любое выражение, начинающееся с цифры, MathCAD интерпретирует как число. Числа набираются на клавиатуры в нужном формате (Рис.1.11). Форматы представлены в окне Format/Result (Рис.1.7.).




Комплексные числа
Комплексное число является суммой действительного и мнимого числа, получающегося путем умножения любого действительного числа на мнимую единицу (imaginary unit) i. По определению полагается, i2=-1. Для ввода мнимой единицы надо нажать клавиши <1>, <i.> (Рис.1.12). Если просто ввести символ "i", то MathCAD интерпретирует его как переменную i.



Размерные значения
В MathCAD числовые переменные и функции могут обладать размерностью. Используется команда Insert / Unit (Вставка / Единицы). "Горячая" клавиша <Ctrl>+<U>. В программе встроено большое количество единиц измерения, с помощью которых и создаются размерные переменные. Для ввода размерного значения - сразу после ввода переменной ввести символ умножения, в окне Insert / Unit списке Unit (Единицы) выбрать нужную единицу измерения
Pедактирование формул
В программе MathCAD при вводе формул курсор имеет вид: синего уголка ("клюшка") . Действие производится только с объектом, выделенным этим уголком. Для того чтобы охватить синим уголком блок, надо нажать на пробел один или несколько раз.


- Набираемая формула всегда заключена в рамку. Не выходите из рамки, пока не закончили набор формулы!
- Для набора формул пользуйтесь "Калькулятором" из "Математической палитры"

При наборе формул возможно появление ошибок набора. Кнопка на стандартной панели инструментов позволяет отменить последнее действие, выполненное при редактировании, т.е. вернуться к тексту, набранному ранее.
Встроенные функции MathCAD
Стандартные математические функции и численные методы, запрограммированные в MathCAD, реализованы в виде встроенных функций. Для вставки функции команда меню Insert /Function (Вставить функцию)(Рис.1.17).

Собственные функции пользователя
Помимо широкого набора стандартных функций в MathCAD возможно определение собственных функций пользователя (Рис.1.14). В простейшем случае функция может быть определена выражением пользователя. Функция определяется следующим образом:
где имя_функции – любой идентификатор; аргументы – список аргументов функции через запятую; выражение – любое выражение с использованием стандартных функций и функций пользователя, определенных в документе перед этим. Выражение должно содержать идентификаторы аргументов. Пример цепочки выражений с использованием функций пользователя приведен ниже:






1.4.2. Массивы
Массивами (arrays) называют упорядоченные последовательности чисел или элементов. Доступ к любому элементу массива возможен по его индексу, т. е. номеру в последовательности чисел В MathCAD условно выделяются два типа массивов: векторы (одноиндексные массивы), матрицы (двухиндексные массивы), и тензоры (многоиндексные массивы); ранжированные переменные (range variables) - векторы, элементы которых определенным образом зависят от их индекса.
Векторы и матрицы
Матрицей размером mxn называется совокупность m•n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m x n записывают так

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы имеют два индекса aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце. Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. Матрицу с одним столбцом называют вектор-столбец, с одной строкой - вектор-строка.
Сложение матриц производится поэлементно, но размеры матриц должны совпадать Умножение матриц. осуществляется по своеобразному закону. Прежде всего, размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

Например, в произведении - матрице C, элемент стоящий в 1-ой строке и 1-м столбце c11, равен сумме произведений элементов 1-ой строки матрицы A и 1 столбца матрицы B,

Создаются матрицы при помощи кнопки палитры инструментов Matrix или команды Insert/Matrix (Рис.1.18, Рис.1.19, Рис.1.20). Появляется окно Insert matrix, где указывается количество строк, столбцов Rows и Columns.
Матрицы в Mathcad
Векторы и матрицы рассматриваются в программе Mathcad как одномерные и двумерные массивы данных.
Матрица создается с помощью диалогового окна Вставить матрицу (рис. 1.6), которое открывают командой Вставка > Матрица (Insert > Matrix) или первой кнопкой на панели "Матрица" (рис. 1.7). Вектор задается как матрица, имеющая один столбец. В диалоговом окне задается число строк и столбцов, а после вставки на рабочий лист матрица содержит вместо элементов заполнители, вместо которых следует вставить число, переменную или выражение.


Для матриц определены сложение, умножение на число, перемножение и другие операции. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы:
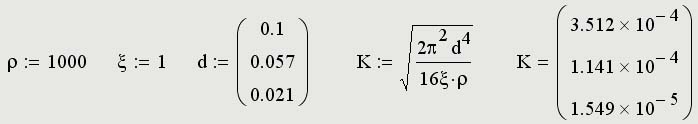
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля, что задается системной переменной ORIGIN, и может быть изменено пользователем (например, блок ORIGIN:=1 устанавливает начальный индекс равным единице). Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Индекс (Subscript, xn) на панели инструментов Mатрица (Matrix) или нажатием символа "[" после имени массива (см. приложение "Горячие клавиши"). Индексы двумерных матриц записываются через запятую.
Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки: . Для его ввода используется кнопка Столбец (Matrix Column) на панели инструментов Матрица или соответствующая "горячая" клавиша.
Для задания некоторой последовательности элементов матрицы используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через точку с запятой значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, например х:=0,0.01..1 . Если разность прогрессии равна единице (то есть, элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают.
На рис. 1.8 приведены примеры реализации некоторых операций с матрицами.
Mathсad имеет более 50 функций, предназначенных для работы с векторами и матрицами. Все функции можно разбить на группы по их функциональному назначению. Например, функции, предназначенные для создания матриц общего и специального вида, редактирования и преобразования матриц, функции, определяющие параметры матриц и т. д. Рассмотрим часть этих функций, которые имеют наибольшее прикладное значение.
Среди функций, предназначенных для создания матриц, следует выделить функцию matrix(L,N,f), где L – число строк матрицы, N – число столбцов матрицы, f – функция f(l,n) при . Другая функция из этой группы identity(n). Функция предназначена для создания единичной матрицы размерности n. Следующая функция geninv(M) позволяет осуществить обращение матрицы M, аналогично операции M -1 .
Для определения размерности матрицы в Mathcad предназначены функция rows(M), определяющая число строк матрицы M, и функция cols(M), определяющая число колонок матрицы M.
Сортировку элементов матрицы осуществляют две функции csort(M,i), rsort(M,j). Функция csort(M,i) обеспечивает сортировку по возрастанию элементов i – го столбца путем перестановки строк, а функция rsort(M,j) – сортировку по возрастанию элементов j –ой строки путем перестановки столбцов.
Для определения минимального и максимального элемента матрицы используются функции min(M) и max(M).
Выделить произвольную подматрицу из матрицы М в Mathcad можно посредством функции submatrix (M, r1, r2, c1, c2), где М – исходная матрица, r1 и r2 –нижний и верхний номер строки матрицы М, включаемых в результирующую подматрицу, а с1 и с2 – нижней и верхний номер столбца матрицы М, включаемых в результирующую подматрицу. Слияние матриц можно осуществить, используя функции augment(A,B,…) и stack(A,B,…). Функция augment(A,B,…) предназначена для слияния матриц А, В и т.д. слева направо. Причем количество строк в матрицах должно быть одинаково. Вторая функция stack(A,B,…) выполняет слияние матриц сверху вниз. Количество столбцов в матрицах должно быть также одинаково. Данные функции могут быть применены и к векторам. На листинге приведен пример использования рассмотренных матричных функций.
С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.
Введение
В предыдущих уроках наши векторы начинались с элемента с номером «0». В этом уроке для простоты сделаем номер первого элемента равным «1». Это можно сделать с помощью вкладки Расчет –> Параметры документа –> ORIGIN:

Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:
Теперь рассмотрим несколько матриц:

Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).
Элемент матрицы можно вывести, используя подстрочные индексы:

Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:

Запомните: первое число – номер строки (или их количество), второе – столбца.
Элементы, выделенные с помощью подстрочных индексов:

Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:

Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:


Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:
Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.
В Mathcad
Для создания вектора или матрицы откройте вкладку Матрицы/таблицы. Когда курсор находится в пустой области щелкните по самой левой кнопке «Вставить матрицу». Появится сетка с маленькими квадратами:

Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:
Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:
Вставку и удаление строк и столбцов легко осуществлять с помощью команд из меню «Операторы с векторами/матрицами» на вкладке Матрицы и таблицы:

Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:

Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:

Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:

Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:
Другие поэлементные операции:

Поэлементные операции применимы только к массивам одного размера.
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:

Эта операция также применима лишь к массивам одного размера.
С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):
Умножение на константу работает так:

При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:

Заметьте, что последовательность множителей играет роль:

Скалярное произведение не коммутативно, за исключением особых случаев:
Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:

Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:

Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.
Обратная матрица определяется только для квадратных матриц:

Произведение матрицы и ее обратной матрицы является единичной матрицей:

Произведение матрицы и единичной матрицы дает изначальную матрицу:


Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:

Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:
Читайте также:


