Размер памяти выделенной для хранения массива вещественных чисел определяет

Обновлено: 24.01.2025

Цель лекции: изучить классификацию типов и их внутреннее представление в языке С++, научиться работать со стандартными и пользовательскими типами .

Основная цель любой программы состоит в обработке каких-либо данных, например, чисел или текстов. Данные могут быть различного вида или типа и, в зависимости от этого, с ними можно выполнять разные действия.

В любом языке программирования каждая константа, переменная , результат вычисления выражения или функции должны иметь определенный тип данных .

Тип данных – это множество допустимых значений, которые может принимать тот или иной объект , а также множество допустимых операций, которые применимы к нему. В современном понимании тип также зависит от внутреннего представления информации.

Таким образом, данные различных типов хранятся и обрабатываются по-разному. Тип данных определяет:

• внутреннее представление данных в памяти компьютера;
• объем памяти, выделяемый под данные;
• множество (диапазон) значений, которые могут принимать величины этого типа;
• операции и функции, которые можно применять к данным этого типа.

Исходя из данных характеристик, необходимо определять тип каждой величины, используемой в программе для представления объектов. Обязательное описание типа позволяет компилятору производить проверку допустимости различных конструкций программы. От выбора типа величины зависит последовательность машинных команд, построенная компилятором.

Классификация типов данных в С++

Современные языки программирования, как правило, могут иметь набор простых типов, являющихся встроенными в данный язык программирования , и средства для создания производных типов.

Объектно-ориентированные языки программирования позволяют определять типы класса.

Реализация простых типов данных заключается в способе представления значений данного типа в компьютере и в наборе операций, поддерживаемых для данного типа.

Тип данных определяет размер памяти, выделяемой под переменную данного типа при ее создании. Язык программирования C++ поддерживает следующие типы данных (рис. 1.1).

• Базовые типы. Базовые типы предопределены стандартом языка , указываются зарезервированными ключевыми словами и характеризуются одним значением. Их не надо определять и их нельзя разложить на более простые составляющие без потери сущности данных. Базовые типы объектов создают основу для построения более сложных типов .
• Производные типы. Производные типы задаются пользователем, и переменные этих типов создаются как с использованием базовых типов, так и типов классов.
• Типы класса. Экземпляры этих типов называются объектами.

Существует четыре спецификатора типа данных, уточняющих внутреннее представление и диапазон базовых типов:

Рассмотрим более подробно базовые типы данных .

Целочисленный (целый) тип данных (тип int)

Переменные данного типа применяются для хранения целых чисел ( integer ). Описание переменной , имеющей тип int , сообщает компилятору, что он должен связать с идентификатором (именем) переменной количество памяти, достаточное для хранения целого числа во время выполнения программы.

Границы диапазона целых чисел, которые можно хранить в переменных типа int , зависят от конкретного компьютера, компилятора и операционной системы (от реализации). Для 16-разрядного процессора под него отводится 2 байта, для 32-разрядного – 4 байта.

Для внутреннего представления знаковых целых чисел характерно определение знака по старшему биту (0 – для положительных, 1 – для отрицательных). Поэтому число 0 во внутреннем представлении относится к положительным значениям. Следовательно, наблюдается асимметрия границ целых промежутков.

В целочисленных типах для всех значений определены следующий и предыдущий элементы. Для максимального следующим значением будет являться минимальное в этом же типе, предыдущее для минимального определяется как максимальное значение . То есть целочисленный диапазон условно можно представить сомкнутым в кольцо. Поэтому определены операции декремента для минимального и инкремента для максимального значений в целых типах .

От количества отводимой под объект памяти зависит множество допустимых значений, которые может принимать объект :

• short int – занимает 2 байта, следовательно, имеет диапазон от –32 768 до +32 767;
• int – занимает 4 байта, следовательно, имеет диапазон от –2 147 483 648 до +2 147 483 647;
• long int – занимает 4 байта, следовательно, имеет диапазон от –2 147 483 648 до +2 147 483 647;
• long long int – занимает 8 байтов, следовательно, имеет диапазон от –9 223 372 036 854 775 808 до +9 223 372 036 854 775 807.

Модификаторы signed и unsigned также влияют на множество допустимых значений, которые может принимать объект :

• unsigned short int – занимает 2 байта, следовательно, имеет диапазон от 0 до 65 535;
• unsigned int – занимает 4 байта, следовательно, имеет диапазон от 0 до 4 294 967 295;
• unsigned long int – занимает 4 байта, следовательно, имеет диапазон от 0 до 4 294 967 295;
• unsigned long long int – занимает 8 байтов, следовательно, имеет диапазон от 0 до 18 446 744 073 709 551 615.

Приведем несколько правил, касающихся записи целочисленных значений в исходном тексте программ.

• Нельзя пользоваться десятичной точкой. Значения 26 и 26.0 одинаковы, но 26.0 не является значением типа int .
• Нельзя пользоваться запятыми в качестве разделителей тысяч. Например, число 23,897 следует записывать как 23897.
• Целые значения не должны начинаться с незначащего нуля. Он применяется для обозначения восьмеричных или шестнадцатеричных чисел, так что компилятор будет рассматривать значение 011 как число 9 в восьмеричной системе счисления .

На практике рекомендуется использовать основной целый тип , то есть тип int . Данные основного целого типа практически всегда обрабатываются быстрее, чем данные других целых типов. Короткий тип short подойдет для хранения больших массивов чисел с целью экономии памяти при условии, что значения элементов не выходят за предельные границы для этих типов. Длинные типы необходимы в ситуации, когда не достаточно типа int .

Вещественный (данные с плавающей точкой) тип данных (типы float и double)

Для хранения вещественных чисел применяются типы данных float (с одинарной точностью) и double (с двойной точностью). Смысл знаков "+" и "-" для вещественных типов совпадает с целыми. Последние незначащие нули справа от десятичной точки игнорируются. Поэтому варианты записи +523.5, 523.5 и 523.500 представляют одно и то же значение .

Для представления вещественных чисел используются два формата:

В большинстве случаев используется тип double , он обеспечивает более высокую точность , чем тип float . Максимальную точность и наибольший диапазон чисел достигается с помощью типа long double .

Величина с модификатором типа float занимает 4 байта. Из них 1 бит отводится для знака, 8 бит для избыточной экспоненты и 23 бита для мантиссы . Отметим, что старший бит мантиссы всегда равен 1, поэтому он не заполняется, в связи с этим диапазон модулей значений переменной с плавающей точкой приблизительно равен от 3.14E–38 до 3.14E+38.

Величина типа double занимает 8 байтов в памяти. Ее формат аналогичен формату float . Биты памяти распределяются следующим образом: 1 бит для знака, 11 бит для экспоненты и 52 бита для мантиссы . С учетом опущенного старшего бита мантиссы диапазон модулей значений переменной с двойной точностью равен от 1.7E–308 до 1.7E+308.

В $60$-х и $70$-х гг. не было единопризнанного стандарта представления чисел с плавающей запятой, из-за чего программы того времени не были переносимыми приложениями. Также большой проблемой были «странности» разных компьютеров, которые нужно было знать и учитывать при создании программ.

В $1976$ году была появилась инициатива создать единый стандарт для представления чисел с плавающей запятой, что существенно упростило работу с числами.

Вычисления компьютера ограничены его памятью, поэтому дробная часть вещественных чисел не является бесконечной и хранится в памяти с определенной точностью.

Числа в нормализованном виде чаще всего записываются только на экране компьютера, поэтому принято запятую в них заменять на точку.

Принятый способ хранения вещественных (действительных) чисел в памяти компьютера использует нормализованную (экспоненциальную) запись действительных чисел.

Для хранения вещественных чисел (как и для целых) используется двоичная система. Таким образом, число предварительно должно быть переведено двоичный код.

Нормализованная запись числа

является нормализованной записью отличного от нуля действительного числа,

где $n$ -- любое целое число (в том числе и ноль),

$m$ -- правильная дробь в системе счисления с основой $q$, у которой первая цифра после запятой не равна нулю, то есть $\frac\le m

$m$ называется мантиссой числа, $n$ -- порядком числа, $q$ -- основанием системы счисления.

Приведем числа десятеричной системы к нормализованной записи:

\[1.3579=0.13579\cdot ^1;\] \[10000=0.1\cdot ^5;\] \[0,123456=0.123456\cdot ^0.\]

Приведем число восьмеричной системы счисления к нормализованной записи:

$_8=_8\cdot 8^$ (порядок записан в десятичной системе).

Приведем число двоичной системы счисления к нормализованной записи:

Готовые работы на аналогичную тему

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Ноль в десятичной системе будет записан в нормализованном виде следующим образом:

Нормализованная экспоненциальная запись (НЭЗ) числа - это запись в виде

где $n$ -- любое целое число (в том числе и ноль),

$m$ -- правильная дробь в системе счисления с основой $q$, целая часть которой состоит из одной цифры,

$m$ --мантисса числа, а $n$ -- порядок (или экспонента) числа.

Рассмотрим вышеописанные числа в нормализованной экспоненциальной записи.

НЭЗ десятичных чисел:

\[1.3579=0.13579\cdot ^1=1.3579\cdot ^0;\] \[10000=0.1\cdot ^5=1.0\cdot ^4;\] \[0.123456=0.123456\cdot ^0=1.23456\cdot ^.\]

НЭЗ восьмеричного числа:

НЭЗ двоичного числа:

Обратите внимание, что в НЭЗ записи первая цифра после запятой может быть нулём, в отличие от нормализованной записи.

Хранение чисел с плавающей запятой

Для хранения вещественных чисел в памяти компьютера часть разрядов ячейки отводится для записи порядка числа, остальные -- для записи мантиссы. По одному разряду в каждой группе разрядов отводится для знака порядка и знака мантиссы. Чтобы не хранить знак порядка был придуман смещенный порядок.

Если для задания порядка выделено k разрядов, то к истинному порядку (ИП) прибавляют смещение, таким образом, смещённый порядок (СП) рассчитывается по формуле:

Найдем смещённый порядок для истинного порядка, лежащего в диапазоне от $-127$ до $+128$.

Возьмем начальное значение ИП= $-127$:

Возьмем конечное значение ИП = $128$:

Таким образом, ИП, лежащий в диапазоне от $-127$ до $+128$, представляется смещённым порядком, значения которого меняются в диапазоне от $0$ до $255$.

Алгоритм представления вещественного числа:

Перевести число в двоичную систему счисления.

Привести число к нормализованной записи.

Найти смещённый порядок числа.

Поместить знак, порядок и мантиссу в соответствующие разряды.

Представим число $-25.625$ в $4$-байтовом представлении ($1$ бит отводится под знак числа, $8$ бит -- под смещённый порядок, остальные биты -- под мантиссу).

Привет! В сегодняшней лекции расскажем о числах в Java, а конкретно — о вещественных числах. Без паники! :) Никаких математических сложностей в лекции не будет. Будем говорить о вещественных числах исключительно с нашей, «программистской» точки зрения. Итак, что же такое «вещественные числа»? Вещественные числа — это числа, у которых есть дробная часть (она может быть нулевой). Они могут быть положительными или отрицательными. Вот несколько примеров: 15 56.22 0.0 1242342343445246 -232336.11 Как же устроено вещественное число? Достаточно просто: оно состоит из целой части, дробной части и знака. У положительных чисел знак обычно не указывают явно, а у отрицательных указывают. Ранее мы подробно разобрали, какие операции над числами можно совершать в Java. Среди них было много стандартных математических операций — сложение, вычитание и т. д. Было и кое-что новое для тебя: например, остаток от деления. Но как именно устроена работа с числами внутри компьютера? В каком виде они хранятся в памяти?

Хранение вещественных чисел в памяти

Думаю, для тебя не станет открытием, что числа бывают большими и маленькими :) Их можно сравнивать друг с другом. Например, число 100 меньше числа 423324. Влияет ли это на работу компьютера и нашей программы? На самом деле — да . Каждое число представлено в Java определенным диапазоном значений :

Тип	Размер в памяти (бит)	Диапазон значений
byte	8 бит	от -128 до 127
short	16 бит	от -32768 до 32767
char	16 бит	беззнаковое целое число, которое преставляет собой символ UTF-16 (буквы и цифры)
int	32 бита	от -2147483648 до 2147483647
long	64 бита	от -9223372036854775808 до 9223372036854775807
float	32 бита	от 2 -149 до (2-2 -23 )*2 127
double	64 бита	от 2 -1074 до (2-2 -52 )*2 1023

Сегодня поговорим именно о последних двух типах — float и double . Оба выполняют одну и ту же задачу — представляют дробные числа. Их еще очень часто называют « числа с плавающей точкой» . Запомни этот термин на будущее :) Например, число 2.3333 или 134.1212121212. Довольно странно. Ведь получается, нет никакой разницы между этими двумя типами, раз они выполняют одну и ту же задачу? Но разница есть. Обрати внимание на столбец «размер в памяти» в таблице выше. Все числа (да и не только числа — вообще вся информация) хранится в памяти компьютера в виде битов. Бит — это самая маленькая единица измерения информации. Она довольно проста. Любой бит равен или 0, или 1. Да и само слово « bit » происходит от английского « binary digit » — двоичное число. Думаю, ты наверняка слышал о существовании двоичной системы счисления в математике. Любое привычное нам десятичное число можно представить в виде набора единиц и нулей. Например, число 584.32 в двоичной системе будет выглядеть так: 100100100001010001111 . Каждые единица и ноль в этом числе являются отдельным битом. Теперь тебе должна быть более понятна разница между типами данных. Например, если мы создаем число типа float , в нашем распоряжении есть всего 32 бита. При создании числа float именно столько места будет выделено для него в памяти компьютера. Если же мы хотим создать число 123456789.65656565656565, в двоичном виде оно будет выглядеть так: 11101011011110011010001010110101000000 . Оно состоит из 38 единиц и нулей, то есть для его хранения в памяти нужно 38 бит. В тип float это число просто не «влезет»! Поэтому число 123456789 можно представить в виде типа double . Для его хранения выделяется целых 64 бита: это нам подходит! Разумеется, и диапазон значений тоже будет подходящим. Для удобства ты можешь представлять число как маленький ящик с ячейками. Если ячеек хватает для хранения каждого бита, значит, тип данных выбран правильно :)
Разумеется, разное количество выделяемой памяти влияет и на само число. Обрати внимание, что у типов float и double отличается диапазон значений. Что это означает на практике? Число double может выразить большую точность, чем число float . У 32-битных чисел с плавающей точкой (в Java это как раз тип float ) точность составляет примерно 24 бита, то есть около 7 знаков после запятой. А у 64-битных чисел (в Java это тип double ) — точность примерно 53 бита, то есть примерно 16 знаков после запятой. Вот пример, который хорошо демонстрирует эту разницу: Что мы должны получить здесь в качестве результата? Казалось бы, все довольно просто. У нас есть число 0.0, и мы 7 раз подряд прибавляем к нему 0.1111111111111111. В итоге должно получиться 0.7777777777777777. Но мы создали число float . Его размер ограничен 32 битами и, как мы сказали ранее, он способен отобразить число примерно до 7 знака после запятой. Поэтому в итоге результат, который мы получим в консоли, будет отличаться от того, что мы ожидали: Число как будто было «обрезано». Ты уже знаешь как хранятся данные в памяти — в виде битов, поэтому тебя не должно это удивлять. Понятно, почему это произошло: результат 0.7777777777777777 просто не влез в выделенные нам 32 бита, поэтому и был обрезан так, чтобы поместиться в переменную типа float :) Мы можем изменить тип переменной на double в нашем примере, и тогда итоговый результат не будет обрезан: Здесь уже 16 знаков после запятой, результат «уместился» в 64 бита. Кстати, возможно ты заметил, что в обоих случаях результаты получились не совсем корректными? Подсчет был произведен с небольшими ошибками. О причинах этого мы поговорим ниже :) Теперь скажем пару слов о том, как можно сравнить числа между собой.

Сравнение вещественных чисел

Мы частично уже затрагивали этот вопрос в прошлой лекции, когда говорили об операциях сравнения. Такие операции как > , < , >= , <= повторно разбирать мы не будем. Вместо этого рассмотрим более интересный пример: Как ты думаешь, какое число будет выведено на экран? Логичным ответом был бы ответ: число 1. Мы начинаем отсчет с числа 0.0 и последовательно прибавляем к нему 0.1 десять раз подряд. Вроде все правильно, должна получиться единица. Попробуй запустить этот код, и ответ сильно тебя удивит :) Вывод в консоль: Но почему в таком простом примере возникла ошибка? О_о Тут бы даже пятиклассник с легкостью верно ответил, но программа на Java выдала неточный результат. «Неточный» тут более подходящее слово, чем «неправильный». Мы все-таки получили очень близкое к единице число, а не просто какое-то рандомное значение :) Оно отличается от правильного буквально на миллиметр. Но почему? Возможно, это просто разовая ошибка. Может, комп заглючил? Попробуем написать другой пример. Вывод в консоль: Так, дело явно не в глюках компа :) Что происходит? Подобные ошибки связаны с тем, как числа представлены в двоичном виде в памяти компьютера. Дело в том, что в двоичной системе невозможно точно представить число 0,1 . В десятичной системе, кстати, тоже есть подобная проблема: в ней нельзя правильно представить дроби (и вместо ⅓ мы получим 0.33333333333333…, что тоже не совсем правильный результат). Казалось бы, мелочь: при таких подсчетах разница может быть в одну стотысячную часть (0,00001) или даже меньше. Но что, если от этого сравнения будет зависеть весь результат работы твоей Очень Серьезной Программы? Мы явно ожидали, что два числа будут равны, но из-за особенностей внутреннего устройства памяти мы отменили запуск ракеты. Раз так, нам нужно определиться, как же все-таки сравнить два числа с плавающей точкой, чтобы результат сравнения был более. эммм. предсказуемым. Итак, правило №1 при сравнении вещественных чисел мы уже усвоили: никогда не используй == при сравнении чисел с плавающей точкой. Ок, плохих примеров, думаю, достаточно :) Давай рассмотрим хороший пример! Здесь мы по сути делаем то же самое, но меняем способ сравнения чисел. У нас есть специальное «пороговое» число — 0.0001, одна десятитысячная. Оно может быть и другим. Это зависит от того, насколько точное сравнение тебе нужно в конкретном случае. Можно сделать его и больше, и меньше. С помощью метода Math.abs() мы получаем модуль числа. Модуль — это значение числа независимо от знака. Например, у чисел -5 и 5 модуль будет одинаковым и равен 5. Мы вычитаем второе число из первого, и если полученный результат, независимо от знака, будет меньше того порога, который мы установили, значит наши числа равны. Во всяком случае, они равны до той степени точности, которую мы установили с помощью нашего «порогового числа» , то есть как минимум они равны вплоть до одной десятитысячной. Такой способ сравнения избавит тебя от неожиданного поведения, которое мы увидели в случае с == . Еще один хороший способ сравнения вещественных чисел — использовать специальный класс BigDecimal . Этот класс специально был создан для хранения очень больших чисел с дробной частью. В отличие от double и float , при использовании BigDecimal сложение, вычитание и прочие математические операции выполняются не с помощью операторов ( +- и т.д.), а с помощью методов. Вот как это будет выглядеть в нашем случае: Какой же вывод в консоль мы получим? Мы получили ровно тот результат, на который рассчитывали. И обрати внимание, насколько точными получились наши числа, и сколько знаков после запятой в них уместилось! Гораздо больше, чем во float и даже в double ! Запомни класс BigDecimal на будущее, он тебе обязательно пригодится :) Фух! Лекция получилась немаленькая, но ты справился: молодец! :) Увидимся на следующем занятии, будущий программист!

19 кулона, а скорость света в вакууме составляет 3 ■ 108 м/с.

Однако представление числа с плавающей запятой не един¬ственно. Например, число 23,4 можно записать следующими способами: 2340 • 10 -2 - 234 ■ 10 -1 = 23,4 -10° = 2,34 ■ 10 1 -= 0,234 ■ 102 = 0,0234 ■ 10 3 = . На первый взгляд, выбор очень широкий, однако большинство вариантов обладают серьезными недостатками. В частности,

В англоязычных странах используется термин floating point - плавающая точка, поскольку в этих странах традиционно целая часть отделяется от дробной не запятой, как у нас, а точкой.

все представления,в которых значащая часть содержит нули непосредственно после запятой (2340, 23400 и т.п ) или перед ней ( 2340, 23400 и т.п) не подходят , поскольку, сохраняя эти незначащие нули, мы напрасно увеличиваем разрядность чисел. Согласно математической теории, для обеспечения максимальной точности при сохранении цифр числа в фиксированном количестве разрядов надо выбирать такой метод, при котором значащие цифры числа следует поместить как можно ближе к запятой. С этой точки зрения оптимальным будет вариант, когда целая часть равна нулю, а первая ненулевая цифра находится сразу после запятой (в нашем примере 0,234). При этом вместо двух частей (целой и дробной) остаётся только дробная, что фактически делает ненужной «разделительную» запятую.

Но взгляните на рис. 4.20, а, изображающий такое число на индикаторе: первый разряд всегда равен нулю, что делает его практически бесполезным. Поэтому с точки зрения экономии разрядов лучше взять другой вариант, в котором значащая часть равна 2,34 (рис. 4.20, б). Именно такой выбор закреплён в стан¬дарте IEEE 754 1 , на котором основана арифметика вещественных чисел в современных компьютерах.

Итак, существуют два приблизительно равноценных способа представления чисел с плавающей запятой: оптимальный с теоретической точки зрения, в котором це¬лая часть нулевая, а первая цифра дробной части ненулевая (0,234 ■ 10 2 ); К сожалению, эта «двойственность» порождает некоторую путаницу. В теоретической литературе, как правило, используется первый способ 1 . Все описания конкретных компьютерных систем, напротив, базируются на втором. Причём в обоих случаях обычно используется один и тот же русский термин — мантисса. Зато в англоязычной компьютерной литературе приняты два разных термина: в первом случае значащая часть называется mantissa (слово «мантисса» для математиков однозначно связано с дробной частью числа), а во втором — significand (значащая часть). Далее мы будем использовать второй вариант, поскольку именно он даёт возможность решать задачи, связанные с практическим кодированием вещественных чисел. В связи с этим мы будем применять термин «значащая часть», а не «мантисса».

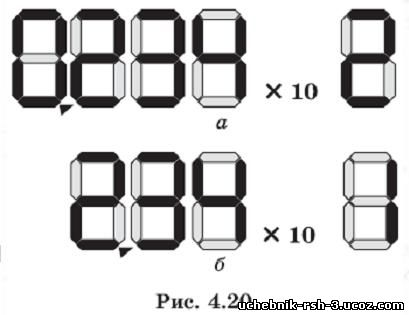
В компьютере используется такое представление вещественных чисел с плавающей запятой, при котором значащая часть Z удовлетворяет условию 1 <Z <B, где В — основание системы счисления. Такое представление называется нормализованным.

Нормализованное представление числа единственно — в нашем примере это 2,34 ■ 10 1 . Любое число может быть легко нор¬мализовано. Единственное, но важное исключение из правила составляет нуль — для него невозможно получить Z > 1. Ради такого важного случая было введено дополнительное соглашение: число 0, в котором все биты нулевые, в качестве исключения считается нормализованным.

Всё сказанное выше можно применить и к двоичной системе: Например: -7₁₀ = -111 ■ 2° = -1,11 ■ 2 10 (не забывайте, что значащая часть и порядок записаны в двоичной системе!); отсюда Z =1,11 и Р = 10. Двоичная значащая часть всегда (исключая, разумеется, ноль!) начинается с единицы, так как 1<Z<2. Поэтому

К этой группе относится большинство отечественных книг по основам вычислительной техники.

во многих компьютерах (в том числе в компьютерах на базе процессоров Intel) эта так называемая скрытая единица не хранится в ОЗУ, что позволяет сэкономить еще один дополнительный разряд значащей части 1 . Идея «скрытой единицы» раньше действительно давала заметное увеличение точности представления чисел, поскольку количество разрядов в устройствах ЭВМ того времени было невелико и поэтому усложнение метода кодирования было оправдано. Сейчас, когда процессоры работают с 64-битными данными, это скорее дань традиции, чем практически полезная мера 2 . Таким образом, при кодировании вещественного числа с плавающей запятой фактически хранятся две величины: его значащая часть (significand) и порядок. От разрядности значащей части зависит точность вычислений, а от разрядности порядка — диапазон представления чисел. В таблице 4.6 приведены характеристики стандартных вещественных типов данных, используемых в математическом сопроцессоре Intel.

Рассмотрим, как «распланированы» 4 байта, отводимые под простейший тип single. Тип double устроен совершенно аналогично, а тип extended, который является основным форматом для

1 В результате то, что осталось после «скрытия» единичной целой части/, можно вполне обоснованно называть мантиссой.

вычислений в математическом сопроцессоре, отличается только тем, что в нём единица в целой части не «скрывается». В числах типа single 23 младших бита (с номерами от О до 22) хранят значащую часть числа, следующие 8 битов (с 23 по 30) — порядок, а старший (31-й) бит отведен под знак числа (рис. 4.21).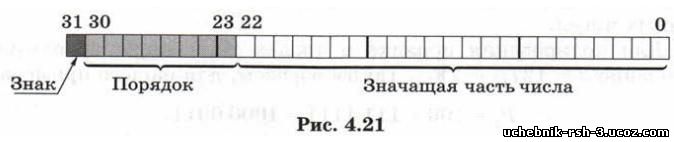

Правила двоичного кодирования вещественных чисел во многом отличаются от правил кодирования целых чисел. Для того чтобы в них разобраться, рассмотрим конкретный пример — закодируем число -17,25 в формате single. Прежде всего, переведём модуль числа в двоичную систему, отдельно целую и дробную части (см. § 11): Для нормализации нужно передвинуть запятую на 4₁₀ = 100₂ Построим значащую часть, «скрыв» единицу в целой части: Так как число отрицательное, знаковый разряд нужно установить в 1, т. е. $=1 В отличие от целых чисел значащая часть вещественных чисел хранится в прямом коде.

Таким образом, значащие части положительного и равного по модулю отрицательного числа одинаковы, а отличаются они только старшим (знаковым) битом.

Теперь остаётся закодировать двоичный порядок 100. Порядок — это целое число со знаком, для него используется кодирование со смещением: чтобы вообще избавиться от знака порядка, к нему добавляют некоторое положительное смещение d: Величина смещения подбирается так, чтобы число Pd было всегда положительным. В этом случае оказывается легче скон¬струировать математический сопроцессор для обработки вещественных чисел. Для кодирования порядка в числах типа single используют смещение d = 127₁₀ = 7F₁₆. Таким образом, для нашего примера Собирая теперь S, Pd и М в единое 32-разрядное число, полу¬чаем: 1 10000011 00010100000000000000000 Не все двоичные комбинации для вещественных чисел соответствуют «правильным »числам: некоторые из них кодируют бесконечные значения, а некоторые — нечисловые данные (англ. NaN — not a number, «не число»). Они отличаются от остальных чисел тем, что имеют максимально возможный порядок 2 <например, для типа single это смещённый порядок P_d — 255, а для типа для double — 2047). Подобные «неправильные» данные возника¬ют только в результате ошибок в вычислениях. Таким образом, мы увидели, что целые и вещественные числа хранятся в памяти компьютера совершенно по-разному. Поэтому неудивительно, что свойства значений, скажем 3 и 3,0, в компьютерной арифметике совершенно различные.

1 На самом деле в IBM-совместимых персональных компьютерах байты будут сохранены в памяти в обратном порядке: 00 00 8А С1.

2 Это вполне логично, поскольку для вещественных чисел переполнение (получение «бесконечного» значения) наступает именно при больших порядках.

Вопросы и задания

1. Чем вызваны трудности, возникающие при представлении вещественных чисел в компьютере? Как они связаны с непрерывностью вещественных чисел в математике?
2. Объясните, как хранятся вещественные числа с фиксированной запятой. Почему этот метод не используется в современных компьютерах?
3. Что такое плавающая запятая? Из каких частей состоит число при кодировании с плавающей запятой?
4. Приведите примеры физических величин, которые обычно записывают в форме с плавающей запятой.
5. Почему метод представления чисел с плавающей запятой неоднозначен? Как изменится порядок, если запятую сместить на один разряд влево (вправо)?
6. Что такое нормализованная форма записи числа?
7. Как требования нормализации связаны с точностью представления вещественных чисел?
8. Единственно ли нормализованное представление числа? Все ли числа имеют нормализованное представление?
9. Почему старший бит значащей части нормализованного двоичного числа всегда равен единице? Как этот факт используется на практике?
10. Какие числа сохраняются в памяти с нулевой значащей частью?
11. На что влияет разрядность значащей части и разрядность порядка?
12. Почему задание разрядности для целых чисел однозначно определяет их свойства, а для вещественных — нет?
13. Что вы знаете о типах single, double и extended?
14. Как хранится порядок во всех рассмотренных форматах вещественных чисел? Почему не хранится знак порядка?
15. Сравните методы хранения отрицательных целых и вещественных чисел.
16. Как по двоичному представлению вещественного числа определить, положительное оно или отрицательное? Подходит ли этот метод для целых чисел?
17. В каком из вещественных форм не используется «скрытая единица» и почему?

18.Какие логические операции и с какой маской надо применить, чтобы в переменной типа single :

а) выделить значащую часть, сбросив порядок и знаковый бит;

б) восстановить в полученной знаковой части «скрытую единицу»?

19. Как можно выделить смещенный порядок из числа типа single? Как получить истинное значение порядка?

20. С помощью какой маски можно выделить знаковый бит числа, хранящегося в формате single?

21. Что такое NaN?

22. Чем различаются представление в памяти целого числа и равного ему вещественного с нулевой дробной частью ( например, 12 и 12,0)?

При записи дробных чисел обращают внимание на точность их представления, т.е. на количество значащихся цифр.

Существуют два типа представления вещественных чисел:

1. С плавающей запятой, точкой – нормальная запись:

Основан на нормальной (экспоненциальной) записи чисел. Число представляется в виде:

Представление числа в формате с плавающей точкой различно.

Пример: 12.3456 = 0,123456*10 2 = 1234,56*10 -2 .

Положение точки в мантиссе определяется величиной порядка p с изменением порядка в большую или меньшую сторону точка перемещается вправо или влево, т.е. “плавает” в изображении числа.

Нормализация при вводе числа и в процессе вычислений осуществляется автоматически. При этом мантисса сдвигается влево на необходимое число разрядов. Происходит соответственно увеличение порядка. При сложении нормального числа одного порядка, может возникнуть переполнение разрядной сетки (появляется 1 слева от запятой). Такого рода переполнение исключается сдвигом мантиссы вправо на 1 разряд и увеличение порядка на 1 единицу. Такая коррекция называется нормализация вправо.

Пример. 4 байтовая ячейка памяти – 24 разряда под мантиссу.

+/-	порядок	Мантисса
1 бит	7 бит	2,3,4 байты
1-й байт

В 1-м байте содержится машинный порядок, в старшем бите хранится знак числа. На порядок отводится 7 бит (2 7 = 128). 128 значений может принимать диапазон значений порядка. Порядок может быть положительным или отрицательным (-64…+63).

В машинном представлении порядок смещен относительно математического и имеет только положительные значения. Смещение формируется так, чтобы минимальному математическому значению порядка соответствовал нуль (0).Связь между машинным и математическим порядком: Мp=p+64₁₀.

Для записи внутреннего представления вещественного числа надо:

1. Перевести модуль данного числа в двоичную систему счисления с 24-мя значащими цифрами.

2. Нормализовать двоичное число.

3. Найти машинный порядок.

4. Учитывая знак числа записать его представление в 4-х байтовом машинном слове.

Пример: 250.1875₁₀ – записать внутреннее представление в 4-х байтовой ячейке.

1. Перевод в двоичную систему с 24 значащими цифрами 250,1875₁₀=11111010,001100000000000000₂ (количество цифр до запятой = 8₁₀ = 1000₂).

Запишем в форме нормализованного двоичного числа с плавающей точкой 0,1111 1010 0011 0000 0000 0000*10 1000 ₂.

Здесь мантисса, основание системы счисления (2₁₀=10₂) и порядок (8₁₀=1000₂) записаны в двоичной системе.

Вычислим машинный порядок: М=1000₂+100 0000₂= 100 1000₂

Запишем в 4-х байтовой ячейки с учетом знака:

0000 0000
1-й байт	2-й байт	3-й байт	4-й байт

2 . С фиксированной запятой, точкой – естественная запись:

Все разряды ячейки кроме знакового служат для изображения разрядов чисел, каждому разряду ячейки соответствует один и тот же разряд числа, что и фиксирует место запятой перед определенным разрядом. Такая система упрощает выполнение арифметических действий, но сильно ограничивает диапазон чисел, которые могут быть представлены в этом типе. Диапазон – 1< x < 1 для представления чисел не укладывающихся в диапазон вводят масштабные коэффициенты. Целые типы данных представляются в ЭВМ в формате с фиксированной запятой.

При работе с вещественными числами надо помнить:

1. При записи чисел возникают ошибки, которые возрастают при операциях.

2. Не разумно сравнивать 2 вещественных числа на точное равенство.

3. В результате вычитания возможна потеря точности.

4. «+» или «–» малого числа может никак не сказаться на результате.

5. Получение очень больших чисел может вызвать переполнение порядка, а очень малые – исчезновение числа.

Диапазон значенийвещественных чисел шире, чем у целых. Наименьшее по абсолютной величине число равно 0, а наибольшее по модулю, это число с самой большой мантиссой и с самыми большим порядком. Множество вещественных чисел в формате с плавающей точкой является ограниченным и дискретным. Количество вещественных чисел, точно представляемых в памяти вычисляется по формуле N = 2 t *(M_pmax = Pmin+1)+1, где

T – количество двоичных разрядов мантиссы

M_pmax – максимальное значение математического порядка.

Pmin – минимальное значение математического порядка.

Пример: для 4-х байтовой ячейки

M_pmax = 63, t = 24, Pmin = -64,

Точность числа – количество значащих цифр, которое удается сохранить в ограниченном числе разрядов.

Читайте также:

  
• Nero 8010l не работает
  
• Основные типы dns зон
  
• Scx 4521f какой тонер
  
• Общее использование можно предоставлять следующие ресурсы компьютера
  
• Можно ли синхронизировать два айфона на одном компьютере