Пространственный перенос компьютерная графика
Четвёртая статья будет разбита на две, первая часть говорит про построение перспективного искажения, вторая про то, как двигать камеру и что из этого следует. Задача на сегодня — научиться генерировать вот такие картинки:

Геометрия на плоскости
Линейные преобразования плоскости
Линейное на плоскости отображение задаётся соответствующей матрицей. Если мы возьмём точку (x,y), то её преобразование записывается следующим образом:
Самое простое (невырожденное) преобразование задаётся единичной матрицей, оно просто оставляет каждую точку на месте
Коэффициенты на диагонали матрицы задают растягивание/сжатие плоскости. Давайте проиллюстрируем картинкой: например, если мы запишем следующее преобразование:
То белый объект (квадрат с отрезанным углом) преобразуется в жёлтый. Красный и зелёный отрезки дают единичные векторы по оси x и y, соответственно.

Все картинки к этой статье сгенерированы вот этим кодом.
Зачем вообще использовать матрицы? Потому что это удобно. Начнём с того, что в матричной форме преобразование всего объекта можно записать вот таким образом:
Здесь преобразование то же, что и в предыдущем примере, а вот матрица в две строки и пять столбцов не что иное, как массив координат нашего куба с обрезанным углом. Мы просто взяли целиком массив, умножили на преобразование, и получили уже преобразованный объект. Красиво? Окей, согласен, притянуто за уши.
Настоящая причина в том, что крайне регулярно мы хотим, чтобы объект подвергся нескольким преобразованиями подряд. Представьте, что вы пишете в вашем коде функции преобразований типа
Этот код делает два линейных преобразования на каждую вершину объекта, а они исчисляются в миллионах. И преобразований зачастую мы хотим с добрый десяток. Дорого. А с матричным подходом мы перемножаем все матрицы преобразования и умножаем на наш объект один раз. В умножении мы можем ставить скобки где хотим, правда ведь?
Продолжаем разговор, мы знаем, что диагональные элементы нам дают масштабирование по осям. За что отвечают два других коэффициента матрицы? Давайте рассмотрим такое преобразование:

Не что иное, как простой сдвиг вдоль оси x. Второй анти-диагональный элемент даст сдвиг вдоль оси y. Таким образом, базовых линейных преобразований на плоскости только два: растягивание по осям и сдвиг вдоль оси. Постойте, скажут мне, а как же, например, вращение вокруг начала координат?
Выясняется, что вращение может быть представлено как композиция трёх сдвигов, здесь белый объект преобразован сначала в красный, затем в зелёный, затем в синий:

Но не будем ударяться в крайности, матрица вращения против часовой стрелки вокруг начала координат может быть записана напрямую (помните про расстановку скобок?):
Перемножать мы можем, конечно, в любом порядке, только давайте не забывать, что для матриц умножение некоммутативно:
Что нормально, сдвинуть и затем повернуть (красный объект) не то же самое, что сначала повернуть, а затем сдвинуть (зелёный объект):

Аффинные преобразования на плоскости
То есть, любое линейное преобразование на плоскости это композиция растягиваний и сдвигов. Что означает, что какой бы ни была матрица нашего преобразования, начало координат всегда перейдёт в начало координат. Таким образом, линейные преобразования — это прекрасно, но если мы не можем представить элементарного параллельного переноса, то наша жизнь будет печальна. Или можем? А что, если добавить его отдельно и записать аффинное преобразование как композицию линейной части и параллельного переноса? Примерно вот так:
Это, конечно, прекрасная запись, но вот только давайте посмотрим, на что похожей выглядит композиция двух таких преобразований (я напоминаю, что в реальной жизни нам нужно уметь аккумулировать десятки преобразований):
Это начинает выглядеть крайне неприятно уже для одной-единственной композиции. Попробуйте преобразовать это выражение, чтобы применить к нашему объекту только одно преобразование вида линейная часть + параллельный перенос. Лично мне очень не хочется этого делать.
Однородные координаты
А что же делать? Колдовать! Представьте теперь, что я допишу руками одну строчку и один столбец к нашей матрице преобразования и добавлю третью координату, которая равна единице у вектора, который мы преобразовываем:
При умножении этой 3x3 матрицы и нашего вектора, дополненного единицей, мы снова получили вектор с единицей в третьей компоненте, а остальные две имеют ровно тот вид, который мы хотели! Колдунство.
На самом деле, идея очень простая: параллельный перенос не является линейной операцией в двумерном пространстве.
Поэтому мы погружаем наше двумерное пространство в трёхмерное (добавив единицу в третью компоненту). Это означает, что наше двумерное пространство это плоскость z=1 внутри трёхмерного. Затем мы делаем линейное преобразование в трёхмерном пространстве и проецируем всё трехмерное пространство обратно на нашу физическую плоскость. Параллельный перенос от этого не стал линеен, но пайплайн всё же прост.
Как именно мы проецируем трёхмерное пространство обратно в нашу плоскость? Очень просто:
Секундочку, но ведь на ноль делить нельзя!
- Мы погружаем наше 2d пространство в 3d, сделав его плоскостью z=1
- Делаем что хотим в 3d
- Для каждой точки, которую хотим спроецировать обратно в 2d, проводим прямую между началом координат и данной точкой и ищем её пересечение с физической плоскостью z=1.

Теперь давайте представим вертикальный рельс, проходящий через точку (x,y,1). Куда спроецируется точка (x,y,1)? Конечно же, в (x,y):

Теперь давайте начнём скользить вниз по рельсу, например, точка (x, y, 1/2) спроецируется в (2x, 2y):

Продолжим скользить: точка (x,y,1/4) спроецируется в (4x, 4y):

Продолжая скользить к нулю по z, наша проекция уходит всё дальше и дальше от центра координат по направлению (x,y).
То есть, точка (x,y,0) проецируется в бесконечно далёкую точку в направлении (x,y). А что это? Правильно, это вектор!
Однородные координаты дают возможность различать вектор и точку. Если программист пишет vec2 v(x,y), это вектор или точка?
Трудно сказать. А в однородных координатах всё, что с нулём по третьей компоненте, это вектор, всё остальное конечные точки.
Смотрите: вектор + вектор = вектор. Вектор-вектор = вектор. Точка + вектор = точка. Ну не здорово ли?
Пример составного преобразования
Я уже говорил, что нам нужно уметь накапливать десятки преобразований. Почему? Предположим, вам нужно повернуть плоский объект вокруг точки (x0, y0). Как это сделать? Можно пойти и искать формулы, а можно сделать самим, ведь у нас есть все инструменты.
Мы умеем вращать вокруг центра координат, мы умеем сдвигать. Что ещё надо? Сдвигаем x0,y0 в центр координат, вращаем, возвращаем назад. Халява!
В 3д последовательности действий будут немного длиннее, но смысл остаётся прежним: нам достаточно уметь делать несколько базовых преобразований, и с их помощью мы можем закодировать какое угодно сложное.
Постойте, а имею ли я право трогать нижнюю строку матрицы 3x3?
Ещё как! Давайте применим вот это преобразование:
к нашему стандартному тестовому объекту. Напоминаю, что тестовый объект белый, единичные икс и игрек вектора показаны красным и зелёным, соответственно

Вот наш преобразованный объект:

И вот тут начинается самое интересное. Помните наше упражнение про игрек-буфер? Здесь мы будем делать практически то же самое.
Мы будем проецировать наш двумерный объект на прямую x=0. Причём теперь усложним задачу: проекция будет центральной, наша камера находится в точке (5, 0) и смотрит в начало координат. Чтобы найти проекцию, мы должны провести прямые, проходящие через точку камеры и каждую вершину нашего объекта (жёлтые прямые), а затем найти их пересечение с прямой экрана (белая вертикальная).

А теперь давайте уберём оригинальный объект и вместо него нарисуем трансформированный.

Если мы используем обычную ортогональную проекцию нашего трансформированного объекта, то мы найдём ровно те же самые точки!
Ведь что делает это отображение? Оно каждое вертикальное ребро оставляет вертикальным, но при этом растягивает те, которые близко к камере, и сжимает те, что дальше от камеры. Правильно подобрав коэффициент растяжения-сжатия мы можем как раз достичь эффекта, что простой ортогональной проекцией мы получаем изображение в перспективном искажении! В следующем параграфе мы добавим одно измерение и покажем, откуда взялся коэффициент -1/5.
Пора перейти к трём измерениям
Давайте объяснять только что произошедшую магию.
Как и в случае двумерных аффинных преобразований, в трёхмерном пространстве мы тоже будем использовать однородные координаты.
Берём точку (x,y,z), погружаем её в четырёхмерное пространство, добавив единицу в четвёртую компоненту, преобразуем в четырёх измерениях и проецируем обратно в 3d. Например, возьмём такое преобразование:
Проекция на 3д даёт следующие координаты:
Хорошо запомним этот результат, но на пару минут его отложим. Давайте вернёмся к стандартному определению центральной проекции в обычном 3д, без однородных координат и прочих экзотических вещей. Пусть у нас будет точка P=(x,y,z), которую мы хотим спроецировать на плоскость z=0, камера находится на оси z на расстоянии c от центра координат.

Мы знаем, что треугольники ABC и ODC подобны. То есть, мы можем записать |AB|/|AC|=|OD|/|OC| => x/(c-z) = x'/c.
Рассматривая треугольники CPB и CP'D, можно легко прийти к подобной записи и для координаты y:
Итак, это очень-очень похоже на результат проекции через однородные координаты, только там это всё считалось одним матричным умножением. Мы вывели зависимость коэффициентов r = -1/c.
Хотя если вы просто возьмёте эту формулу, не поняв весь предыдущий текст, то я вас ненавижу. Итак, если мы хотим построить центральную перспективу с (важно!) камерой, находящейся на оси z на расстоянии c от начала координат, то сначала мы погружаем трёхмерные точки в четырёхмерное пространство, добавив 1. Затем умножаем на следующую матрицу и проецируем результат обратно в 3D:
Мы деформировали наш объект так, что теперь для построения проволочного рендера с перспективой нам достаточно просто забыть про новополученную координату z. Если мы хотим строить z-буфер, то, разумеется, мы её используем. Слепок кода доступен на гитхабе. Результат его работы виден в самом начале нашей статьи.
Четвёртая статья будет разбита на две, первая часть говорит про построение перспективного искажения, вторая про то, как двигать камеру и что из этого следует. Задача на сегодня — научиться генерировать вот такие картинки:

Геометрия на плоскости
Линейные преобразования плоскости
Линейное на плоскости отображение задаётся соответствующей матрицей. Если мы возьмём точку (x,y), то её преобразование записывается следующим образом:
Самое простое (невырожденное) преобразование задаётся единичной матрицей, оно просто оставляет каждую точку на месте
Коэффициенты на диагонали матрицы задают растягивание/сжатие плоскости. Давайте проиллюстрируем картинкой: например, если мы запишем следующее преобразование:
То белый объект (квадрат с отрезанным углом) преобразуется в жёлтый. Красный и зелёный отрезки дают единичные векторы по оси x и y, соответственно.

Все картинки к этой статье сгенерированы вот этим кодом.
Зачем вообще использовать матрицы? Потому что это удобно. Начнём с того, что в матричной форме преобразование всего объекта можно записать вот таким образом:
Здесь преобразование то же, что и в предыдущем примере, а вот матрица в две строки и пять столбцов не что иное, как массив координат нашего куба с обрезанным углом. Мы просто взяли целиком массив, умножили на преобразование, и получили уже преобразованный объект. Красиво? Окей, согласен, притянуто за уши.
Настоящая причина в том, что крайне регулярно мы хотим, чтобы объект подвергся нескольким преобразованиями подряд. Представьте, что вы пишете в вашем коде функции преобразований типа
Этот код делает два линейных преобразования на каждую вершину объекта, а они исчисляются в миллионах. И преобразований зачастую мы хотим с добрый десяток. Дорого. А с матричным подходом мы перемножаем все матрицы преобразования и умножаем на наш объект один раз. В умножении мы можем ставить скобки где хотим, правда ведь?
Продолжаем разговор, мы знаем, что диагональные элементы нам дают масштабирование по осям. За что отвечают два других коэффициента матрицы? Давайте рассмотрим такое преобразование:

Не что иное, как простой сдвиг вдоль оси x. Второй анти-диагональный элемент даст сдвиг вдоль оси y. Таким образом, базовых линейных преобразований на плоскости только два: растягивание по осям и сдвиг вдоль оси. Постойте, скажут мне, а как же, например, вращение вокруг начала координат?
Выясняется, что вращение может быть представлено как композиция трёх сдвигов, здесь белый объект преобразован сначала в красный, затем в зелёный, затем в синий:

Но не будем ударяться в крайности, матрица вращения против часовой стрелки вокруг начала координат может быть записана напрямую (помните про расстановку скобок?):
Перемножать мы можем, конечно, в любом порядке, только давайте не забывать, что для матриц умножение некоммутативно:
Что нормально, сдвинуть и затем повернуть (красный объект) не то же самое, что сначала повернуть, а затем сдвинуть (зелёный объект):

Аффинные преобразования на плоскости
То есть, любое линейное преобразование на плоскости это композиция растягиваний и сдвигов. Что означает, что какой бы ни была матрица нашего преобразования, начало координат всегда перейдёт в начало координат. Таким образом, линейные преобразования — это прекрасно, но если мы не можем представить элементарного параллельного переноса, то наша жизнь будет печальна. Или можем? А что, если добавить его отдельно и записать аффинное преобразование как композицию линейной части и параллельного переноса? Примерно вот так:
Это, конечно, прекрасная запись, но вот только давайте посмотрим, на что похожей выглядит композиция двух таких преобразований (я напоминаю, что в реальной жизни нам нужно уметь аккумулировать десятки преобразований):
Это начинает выглядеть крайне неприятно уже для одной-единственной композиции. Попробуйте преобразовать это выражение, чтобы применить к нашему объекту только одно преобразование вида линейная часть + параллельный перенос. Лично мне очень не хочется этого делать.
Однородные координаты
А что же делать? Колдовать! Представьте теперь, что я допишу руками одну строчку и один столбец к нашей матрице преобразования и добавлю третью координату, которая равна единице у вектора, который мы преобразовываем:
При умножении этой 3x3 матрицы и нашего вектора, дополненного единицей, мы снова получили вектор с единицей в третьей компоненте, а остальные две имеют ровно тот вид, который мы хотели! Колдунство.
На самом деле, идея очень простая: параллельный перенос не является линейной операцией в двумерном пространстве.
Поэтому мы погружаем наше двумерное пространство в трёхмерное (добавив единицу в третью компоненту). Это означает, что наше двумерное пространство это плоскость z=1 внутри трёхмерного. Затем мы делаем линейное преобразование в трёхмерном пространстве и проецируем всё трехмерное пространство обратно на нашу физическую плоскость. Параллельный перенос от этого не стал линеен, но пайплайн всё же прост.
Как именно мы проецируем трёхмерное пространство обратно в нашу плоскость? Очень просто:
Секундочку, но ведь на ноль делить нельзя!
- Мы погружаем наше 2d пространство в 3d, сделав его плоскостью z=1
- Делаем что хотим в 3d
- Для каждой точки, которую хотим спроецировать обратно в 2d, проводим прямую между началом координат и данной точкой и ищем её пересечение с физической плоскостью z=1.

Теперь давайте представим вертикальный рельс, проходящий через точку (x,y,1). Куда спроецируется точка (x,y,1)? Конечно же, в (x,y):

Теперь давайте начнём скользить вниз по рельсу, например, точка (x, y, 1/2) спроецируется в (2x, 2y):

Продолжим скользить: точка (x,y,1/4) спроецируется в (4x, 4y):

Продолжая скользить к нулю по z, наша проекция уходит всё дальше и дальше от центра координат по направлению (x,y).
То есть, точка (x,y,0) проецируется в бесконечно далёкую точку в направлении (x,y). А что это? Правильно, это вектор!
Однородные координаты дают возможность различать вектор и точку. Если программист пишет vec2 v(x,y), это вектор или точка?
Трудно сказать. А в однородных координатах всё, что с нулём по третьей компоненте, это вектор, всё остальное конечные точки.
Смотрите: вектор + вектор = вектор. Вектор-вектор = вектор. Точка + вектор = точка. Ну не здорово ли?
Пример составного преобразования
Я уже говорил, что нам нужно уметь накапливать десятки преобразований. Почему? Предположим, вам нужно повернуть плоский объект вокруг точки (x0, y0). Как это сделать? Можно пойти и искать формулы, а можно сделать самим, ведь у нас есть все инструменты.
Мы умеем вращать вокруг центра координат, мы умеем сдвигать. Что ещё надо? Сдвигаем x0,y0 в центр координат, вращаем, возвращаем назад. Халява!
В 3д последовательности действий будут немного длиннее, но смысл остаётся прежним: нам достаточно уметь делать несколько базовых преобразований, и с их помощью мы можем закодировать какое угодно сложное.
Постойте, а имею ли я право трогать нижнюю строку матрицы 3x3?
Ещё как! Давайте применим вот это преобразование:
к нашему стандартному тестовому объекту. Напоминаю, что тестовый объект белый, единичные икс и игрек вектора показаны красным и зелёным, соответственно

Вот наш преобразованный объект:

И вот тут начинается самое интересное. Помните наше упражнение про игрек-буфер? Здесь мы будем делать практически то же самое.
Мы будем проецировать наш двумерный объект на прямую x=0. Причём теперь усложним задачу: проекция будет центральной, наша камера находится в точке (5, 0) и смотрит в начало координат. Чтобы найти проекцию, мы должны провести прямые, проходящие через точку камеры и каждую вершину нашего объекта (жёлтые прямые), а затем найти их пересечение с прямой экрана (белая вертикальная).

А теперь давайте уберём оригинальный объект и вместо него нарисуем трансформированный.

Если мы используем обычную ортогональную проекцию нашего трансформированного объекта, то мы найдём ровно те же самые точки!
Ведь что делает это отображение? Оно каждое вертикальное ребро оставляет вертикальным, но при этом растягивает те, которые близко к камере, и сжимает те, что дальше от камеры. Правильно подобрав коэффициент растяжения-сжатия мы можем как раз достичь эффекта, что простой ортогональной проекцией мы получаем изображение в перспективном искажении! В следующем параграфе мы добавим одно измерение и покажем, откуда взялся коэффициент -1/5.
Пора перейти к трём измерениям
Давайте объяснять только что произошедшую магию.
Как и в случае двумерных аффинных преобразований, в трёхмерном пространстве мы тоже будем использовать однородные координаты.
Берём точку (x,y,z), погружаем её в четырёхмерное пространство, добавив единицу в четвёртую компоненту, преобразуем в четырёх измерениях и проецируем обратно в 3d. Например, возьмём такое преобразование:
Проекция на 3д даёт следующие координаты:
Хорошо запомним этот результат, но на пару минут его отложим. Давайте вернёмся к стандартному определению центральной проекции в обычном 3д, без однородных координат и прочих экзотических вещей. Пусть у нас будет точка P=(x,y,z), которую мы хотим спроецировать на плоскость z=0, камера находится на оси z на расстоянии c от центра координат.

Мы знаем, что треугольники ABC и ODC подобны. То есть, мы можем записать |AB|/|AC|=|OD|/|OC| => x/(c-z) = x'/c.
Рассматривая треугольники CPB и CP'D, можно легко прийти к подобной записи и для координаты y:
Итак, это очень-очень похоже на результат проекции через однородные координаты, только там это всё считалось одним матричным умножением. Мы вывели зависимость коэффициентов r = -1/c.
Хотя если вы просто возьмёте эту формулу, не поняв весь предыдущий текст, то я вас ненавижу. Итак, если мы хотим построить центральную перспективу с (важно!) камерой, находящейся на оси z на расстоянии c от начала координат, то сначала мы погружаем трёхмерные точки в четырёхмерное пространство, добавив 1. Затем умножаем на следующую матрицу и проецируем результат обратно в 3D:
Мы деформировали наш объект так, что теперь для построения проволочного рендера с перспективой нам достаточно просто забыть про новополученную координату z. Если мы хотим строить z-буфер, то, разумеется, мы её используем. Слепок кода доступен на гитхабе. Результат его работы виден в самом начале нашей статьи.
Сейчас не сложно найти информацию по компьютерной графике. Все уже изложено, описано, и ничего нового в этой статье я не расскажу. Никакого смысла писать статью до недавнего времени не было, пока не появилась статья «Продвинутая графика». Изначально я думал, что автор данной статьи, просто решил не выкладывать теории, а реализовал только практическую часть, на что я и указал в комментариях, что неплохо бы привести ссылку на теорию, и привел примеры тригонометрических преобразований, которые были упущены в статье. На что получил довольно странный ответ, что я оказывается, замкнут в тех знаниях, которые дали мне: школа, институт, самообразование, а для новых знаний я совершенно закрыт. А вот автор не несет на себе столь тяжкий груз знаний и поэтому перед ним открывается мир полный волшебства.
Дальше новатор заявил, что подобное преобразование классическим способом сделать невозможно.
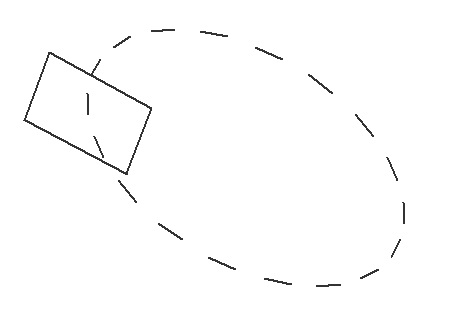
В очередной раз убедился, что дискутировать с подобными личностями бесполезно, все аргументы разбиваются в пропасти отсутствия знаний. Если человек не знаком с тригонометрией, невозможно ему объяснить тригонометрические преобразования.
По ключевым словам «1С, графика» теперь поисковик выдаст столь интересную статью на инфостарте, потом найдется деятель, который напишет статью на другом ресурсе: «1С-ник – не программист, на примере компьютерной графики».
Теория
Все преобразования в данной статье будут рассматриваться в 2-мерной системе координат. Сразу отмечу, что преобразования в 3-мерной системе координат сильно не отличаются. Как правило объекты перемещаются и вращаются. С перемещением в декартовой системе координат все просто - координаты точек изменяются простым и понятным образом. Операция поворот – намного сложнее. Как выполнить преобразование поворот? Вычислить длину вектора, найти текущий угол, добавить угол поворота, получить новые координаты – сложно, но можно упростить.

Рассмотрим поворот точки А на угол d. Начальное положение точки рассмотрим, относительно точки А0 - вектор с 0 градусом поворота. Тогда координаты точки A будут равны:
Координаты точки A1 будут равны
x1 = x0 * cos(c + d)
y1 = x0 * sin(c + d)
cos(c + d) = cos (c) * cos(d) - sin(c) * sin(d)
sin(c + d) = sin(c) * cos(d) + sin(d) * cos(c)
x1 = x0 *cos (c) * cos(d) - x0 *sin(c) * sin(d)
x1 = x * cos (d) – y * sin(d)
y1 = x0 * sin(c) * cos(d) + x0 * sin(d) * cos(c)
y1 = y * cos(d) + x * sin(d)
Получившиеся выражения мы можем представить в виде произведения матриц
Надеюсь в этом месте многим в голову пришел вопрос: «Зачем приводить к произведению матриц?».
Дело в том что у произведения матриц есть свойство ассоциативности, которое выглядит следующим образом A * B * C = A * (B * C). Всего-то порядок действий изменился, но это свойство окажется очень полезным в компьютерной графике, к нему вернемся позже.
Как уже многие догадались, все преобразования мы будем приводить к произведению матриц, с поворотом уже все ясно, как же выполнять остальные преобразования, например, перемещение.
Делается это следующим образом – матрицу точек будем задавать тремя значениями (x, y, 1).
Теперь матрица поворота будет выглядеть следующим образом
Где Tx, Ty смещение по x и y.
Это далеко не весь перечень возможных преобразований, но на этом остановимся, дальше будем рассматривать на примерах.
Примеры графических преобразований
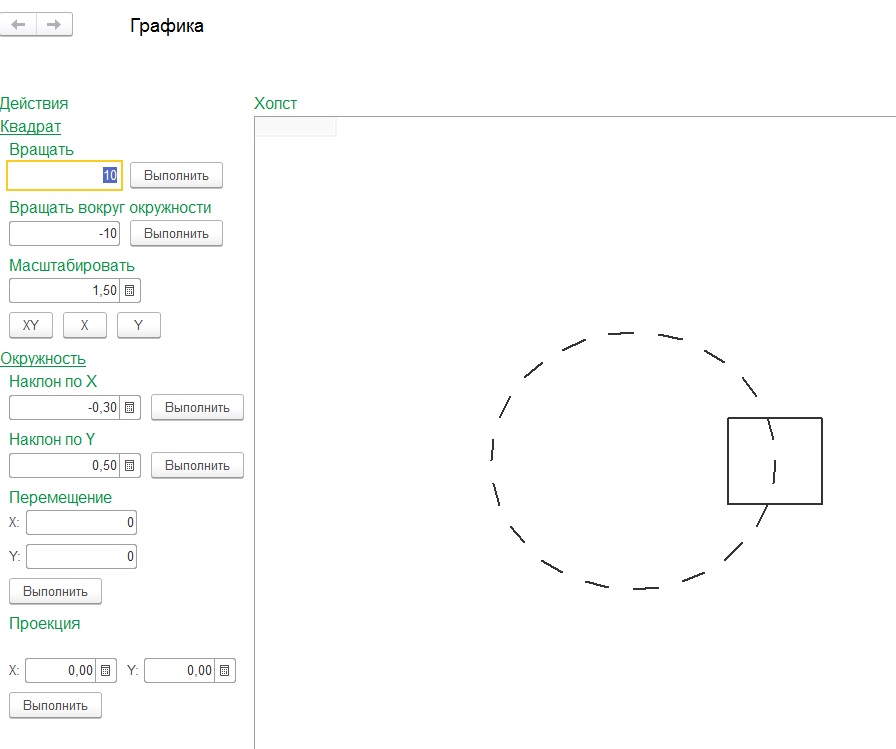
Для демонстрации примеров работы с графикой, я создал обработку в управляемом интерфейсе «графика.epf».
Работать мы будем всего с двумя объектами: окружность и квадрат. Каждый из объектов состоит из прямых линий, линии - состоят из координат концов.
Начало координат я сместил примерно в центр, т.е. окружность расположена в начале координат.
Над квадратом мы будем выполнять следующие преобразования:
- Вращение вокруг центра квадрата.
- Вращение вокруг центра окружности.
Начальное положение квадрата – смещение по X на радиус сферы. Т.е. чтобы получить координаты нужно матрицу М каждой точки, умножить на матрицу преобразования – перемещения T1.
Теперь, допустим мы хотим повращать квадрат вокруг его центра, делать мы это будем следующим образом: сначала переместим квадрат M * T1, затем умножим на матрицу поворота R2

Теперь повернем квадрат относительно своего центра. Т.е. теперь мы должны матрицу М умножить на матрицу поворота R3
Затем умножить на матрицу перемещения T1, а потом снова на матрицу поворота R2.
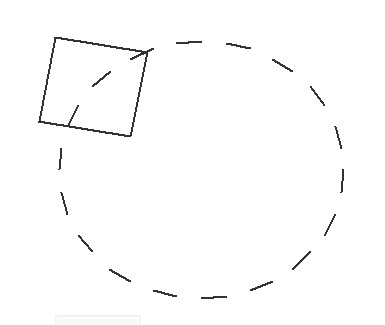
Запишем в другой форме – матрицы преобразования вращения квадрата вокруг центра обозначим K с индексом, вокруг окружности O, а также перемещение квадрата на радиус окружности P.
Тогда преобразования примут вид:
M * K1 * K2 * … * KN * P * O1 * O2 * … ON
воспользуемся свойством ассоциативности
M * (K1 * K2 * … * KN) * (P * O1 * O2 * … ON)
т.е. нам не нужно хранить и каждый раз перемножить все матрицы преобразований, достаточно хранить матрицы преобразований на каждом этапе перехода к новой системе исчисления.
Для квадрата таковых три:
- Вращение вокруг собственного центра (а также масштабирование);
- Вращение по радиусу окружности;
- Перемещение окружности (а также другие преобразования).
Другие преобразования - это, например, проецирование.
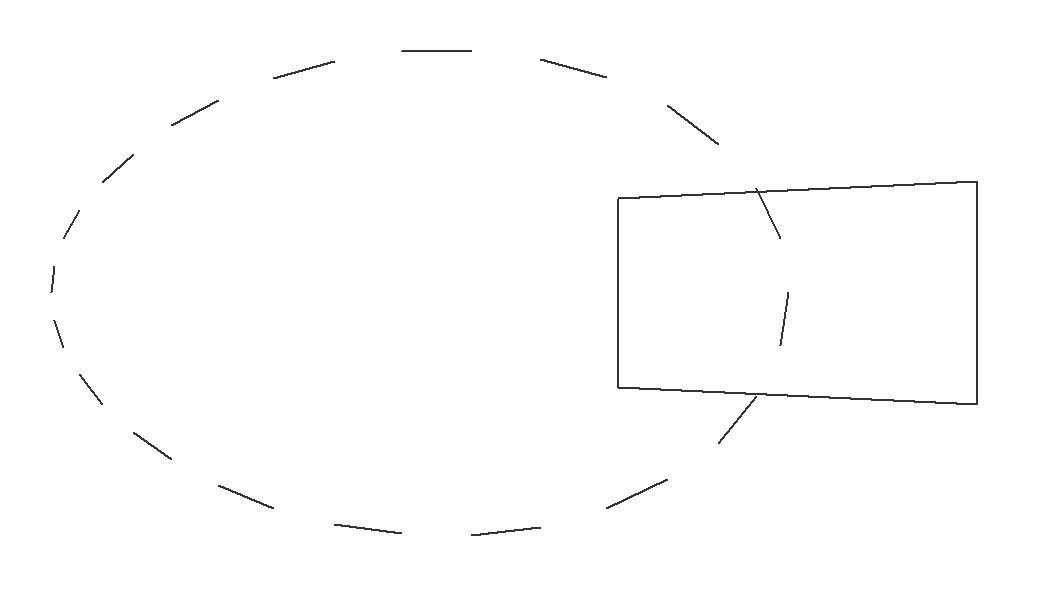
Не знаю где в двухмерной графике может применяться проецирование, но выглядит эффектно, преобразование работает и на окружность, и на квадрат.
Зато в трехмерной графике проецирование – вещь очень важная. Дело в том угол человеческого зрения – не прямой, а как раз мы видим проекцию, т.е. чем дальше от нас предмет, тем он меньше, подобным образом трехмерное изображение проецируется на плоскость монитора.
После умножения матрицы координат точки на матрицу проецирования – изменится третье значение матрицы координат, которое обычно равняется 1. В данном случае, третье значение будет отличаться от 1, матрица координат примет вид (x, y, s). Что делать с третьим значением? Нужно каждую координату умножить на полученный коэффициент s.
Трехмерная графика
Если статья окажется интересной для посетителей Инфостарта, в следующей статье напишу про основы трехмерной графики, там тоже есть интересные моменты.
Читайте также:


