Построение кривой обеспеченности в экселе
Для селекционера, например, важно знать, сколько зерен содержит колос выведенного (выводимого) им нового сорта пшеницы. В этой ситуации совершенно ясно, что подсчетом количества зерен только в одном колосе не обойтись. Для определения числа зерен надо воспользоваться достаточно большим количеством колосьев, скажем не менее сотни. Приведем пример математической обработки результатов селекции.
Все поле пшеницы, которое вырастил селекционер можно на математическом языке назвать генеральной совокупностью. Подсчитать количество зерен в колосьях всей генеральной совокупности, очевидно, не представляется возможным, но из всей генеральной совокупности можно выбрать, скажем, сто колосьев и подсчитать количество зерен в них. Эти сто колосьев будут называться выборкой из генеральной совокупности, и они с определенной точностью будут отражать число зерен во всем поле (генеральной совокупности). Чтобы по данным выборки иметь возможность судить обо всей генеральной совокупности, она должна быть отобрана случайно. Так в нашем случае селекционер ни в коем случае не должен отдавать предпочтение тем или иным колосьям (по размерам, внешнему виду, месту произрастания на поле и т.п.) в процессе их выборки. Наиболее целесообразно в данной ситуации совершать выбор колосьев из непрозрачного мешка наугад. У всех выбранных колосьев производится подсчет числа зерен, и результаты фиксируются в виде ряда чисел, с которыми в дальнейшем и предстоит совершать математические действия. В данном примере можно предложить следующую их последовательность.
2.1 Создание вариационного ряда.
Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами или частностями). Вариационный ряд будет дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным, если варианты могут отличатся один от другого на сколь угодно малую величину.
Иными словами в вариационном ряду полученные значения располагаются в порядке их увеличения и, если значение повторяется, то рядом записывается число его повторений. Т.е. в данном примере по числу зерен в колосьях ряд может выглядеть так (таб. 2):
В данной статье, на примере, рассмотрим такой вид диаграммы, как График с накоплением и в чем его отличие от обычного Графика.
Предположим у нас есть таблица, в которой отражены продажи офисных стульев за год, в штуках. Продажи осуществляли два магазина: Магазин № 1 и магазин № 2.

Это будет наша исходная таблица, на основе которой мы будем строить график с накоплением.
График с накоплением в Excel.
Перед построением графика нам необходимо выделить всю таблицу. Потом в закладке Вставка находим значок Вставить график или диаграмму с областями.


Нажимаем и получаем График с накоплением.

На графике отразились две кривые линии. Оранжевая кривая, это продажи Магазина №2. Синяя кривая, это продажи магазина №1. Для наглядности добавим Метки данных. Вызовем настройки диаграммы нажав на нее. В настройках выберем Элементы диаграммы. Поставим галочку напротив пункта Метки данных. На нашем графики отразиться количество проданных стульев соответственно месяцу года и магазину.

Вертикальная ось диаграммы показывает количество проданных стульев. При этом оранжевая кривая на графике, которая соответствует продажам Магазина №2, берет свое начало не на отметке 260 (шт.). Это количество проданных стульев данным магазинов в январе. Оранжевая кривая берет сове начало на отметке 510 (шт.). Это суммарное количество проданных стульев двумя магазинами в январе (250 шт. +.260 шт.). То есть, для оранжевой кривой, при определении координаты по вертикальной оси, начало отсчета происходит не от нулевой отметки, а от соответствующей (нижележащей) точки синей кривой.
Построим на основе исходной таблицы простой График.

Как видно, кривые продаж Магазина №1 и Магазина №2 наложились одна на одну. Проводить анализ или презентацию используя такой график не целесообразно. График с накоплением позволяет избежать данной проблемы.
По роду своей деятельности большинство специалистов, задействованных в области инженерных изысканий, и инженеры-геологи в частности, сталкиваются с большим количеством данных. Такие данные для удобства иногда располагаются в таблицах, которые можно наблюдать, к примеру, в нормативной документации. Но порой массива данных бывает недостаточно для получения необходимых значений и здесь на помощь в некоторых случаях может прийти такой математический инструмент, как интерполяция.
Поэтому возникла идея подготовки и публикации данного материала. В нем рассмотрена одна из возможностей использования программы Excel для нахождения промежуточных значений, которая входит в стандартный пакет MS Office, установленный в большинстве компаний.
Вы научитесь делать это самостоятельно, создадите свой файл с расчетами, оцените все его преимущества и сведете к минимуму так называемый человеческий фактор. Сам материал изложен общедоступным языком, а формулы упрощены для лучшего их понимания.
Все примеры приводятся в русскоязычной версии MS Office Excel 2013, однако и в более ранних большинство формул должно работать, возможно, за исключением тех, в которых будет задано большое количество условий.
Введение
Интерполяция – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. И в университете, на парах математики вы с ней скорее всего знакомились.
Вариантов интерполяции существует некоторое множество, но мы будем рассматривать именно линейную интерполяцию, которую в Excel можно выполнять с помощью функции ПРЕДСКАЗ. Стоит отметить, что сама эта функция имеет более широкие возможности.
Сначала мы будем использовать не все данные из этой таблицы, а только часть. Например – значения moed для супесей при коэффициенте пористости e 0,65-0,75. Создайте такую же таблицу в Excel. Обратите внимание, что содержимое должно соответствовать тем же строкам и столбцам, что и в примере.
На оси X в данном случае будут располагаться значения коэффициента пористости e , а на оси Y – коэффициента moed , соответственно. Посаженные по координатам точки будут соединены отрезком, который мы условно обозначим ab (рис.1).

Давайте представим, что нам необходимо найти moed для супеси с коэффициентом пористости 0,7. Для этого от числа 0,7 на оси X мы проведем параллельную оси Y линию fc до нашего отрезка. Затем от точки пересечения проведем к оси Y уже параллельно оси X линию cd . И получим значение moed – 2,3 графику (рис. 2).

Это графический способ. Математически формула линейной интерполяции в данном случае выглядит так:
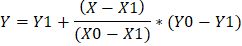
где Y0=2,1; Y1=2,5; X=0,7; X0=0,75; X1=0,65
На рисунке 3 приведена диаграмма с соответствующими обозначениями.

Подставив все эти значения в формулу, получаем:
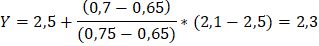
Y – есть наше искомое значение moed для коэффициента пористости 0,70, которое для супеси равно 2,3.
Удобен ли такой расчет на листе бумаги? Не очень, т.к. отнимает много времени. Однако уже хорошо, что он вообще выполняется.
На данный момент, когда уже понятно, как выглядит линейная интерполяция графически и как она рассчитывается математически, для упрощения используем функцию ПРЕДСКАЗ, которая может сделать то же самое для двух наших значений e и соответствующих им moed .
Сама функция в Excel имеет следующий вид:
ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x)
Возвращаемся к нашему примеру и в ячейку M5 запишем известное значение коэффициента пористости – 0,70, а в ячейку N5 впишем следующую формулу:
=ПРЕДСКАЗ(M5;M3:N3;M2:N2)
Нажмем Enter. В результате в ячейке N5 получим значение 2,3, которое соответствует нашему искомому коэффициенту moed . Изменяя значение в ячейке M5 от 0,65 до 0,75, вы будете получать в соответствии с ним новые значения в ячейке N5 (рис. 4).

Теперь полностью автоматизируем расчеты и разберем на примерах различные варианты. Для каждого из них создадим отдельный лист в книге Excel.
Важно! Все значения должны быть размещены в тех же строках и столбцах, что и в примерах.
Пример 1. Получение коэффициента moed

Так как зависимость значений в таблице не линейная и это наглядно видно, если построить по ним все ту же диаграмму и выполнить линейную аппроксимацию (рис. 6, 7, 8), мы не можем взять сразу весь массив данных.



Поэтому сначала выберем по два значения, внутри диапазона которых будет проведена интерполяция. А затем сделаем это для всех данных из таблицы по очереди.
Далее будет указано, в какую ячейку, какое содержимое вписывать. Формат ячеек может быть, как общий, так и числовой.

Затем для большего удобства сделаем выбор типа грунта из выпадающего списка. Для этого:
Выберите ячейку B2
Остается только получить нужный результат. Впишите формулу в ячейку B6:
Если вы все сделали правильно, то ваш лист Excel должен иметь следующий вид (рис. 11):

Стоит отметить, что добиться подобного можно и другими способами. Например, используя связку функций Excel: ГПР, ИНДЕКС и ПОИСКПОЗ. При этом не потребуется интерполировать всю таблицу, а условных операторов будет меньше. Рассмотрим этот вариант ниже.
Пример 2. Получение расчетного сопротивления глинистых непросадочных грунтов

Далее будет указано, в какую ячейку, какое содержимое вписывать. Формат ячеек может быть как общий, так и числовой.

Остается только получить R0 . Для этого впишите такую формулу в ячейку B5 :
В результате лист Excel должен иметь следующий вид (рис. 13).

Как можно заметить, в этом примере для того чтобы не выполнять поочередную интерполяцию всех значений таблицы, были использованы функции ВПР, ИНДЕКС и ПОИСКПОЗ, что значительно упростило задачу. Изменяя тип грунта, а так же значения в ячейках B3 и B4 , вы неизменно получите значение расчетного сопротивления в ячейке B5 .
Пример 3. Косвенный метод определения плотности p песков по результатам статического зондирования
В качестве альтернативы лабораторному методу определения плотности природного сложения аллювиальных и флювиогляциальных песков, залегающих на глубине до 6 м, Л.Г. Мариупольским была предложена возможность определения p с помощью результатов статического зондирования, природной влажности ( W ) и плотности частиц грунта ( ps ). Сопоставив 171 определение коэффициента пористости е , полученного в лабораторных условиях из ненарушенных образцов проб песка с сопротивлением конусу ( qc ) зонда II типа этих же грунтов, выведена следующая корреляционная зависимость:
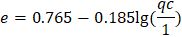
где 1 – это 1 МПа.
По утверждениям автора, коэффициент корреляции для такой зависимости составил 0,74, а среднее квадратическое отклонение – 0,09. Причем гранулометрический состав в таком случае практически не влияет на точность определения e .
Исходя из вышесказанного, получена формула количественного определения плотности p таких песков:
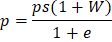
ps - плотность частиц грунта;
W - влажность грунта;
e – коэффициент пористости.
Если подставить в эту формулу коэффициент пористости, то получится следующее:
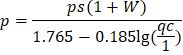
Т.к. для определения W и ps нет необходимости отбирать образцы ненарушенной структуры, то, по утверждениям автора, точности результатов p по данной формуле достаточно для расчетов оснований свайных фундаментов.
В следствии этого была представлена таблица, в которой приведены значения плотности p песков в зависимости от их qc и W .
Таблица 1. Значения плотности песков p в зависимости от сопротивления конусу зонда qc и влажности W по Мариупольскому

Для расчета значений в этой таблице, плотность частиц песков принималась, как средняя, ps =2,65 г/см 3 .
Это было небольшое отступление. В данном примере не рассматривается вариант применения такого расчета для определения плотности песков. Цель – показать возможность интерполяции по двум неизвестным, для которого хорошо подходит такая таблица.
Теперь перенесем ее на новый лист Excel. Чтобы еще немного усложнить задачу, расположим значения в строке qc от большего к меньшему. Соответственно, значения p тоже перенесем (рис. 14).

Далее ход действий такой же, как и в предыдущих примерах. Формат ячеек может быть, как общий, так и числовой.

Теперь обработаем результаты, а заодно рассчитаем такие показатели, как плотность сухого грунта pd , коэффициент пористости e и коэффициент водонасыщения Sr .

Дополнительно, помимо простой интерполяции, выполним расчет p по тем формулам, которые указывались выше:

Теперь, лист Excel у вас должен иметь следующий вид (рис. 15)

Изменяя значения в ячейках B1 , B2 и B3 , вы будете получать значения как по результатам интерполяции таблицы, так и по результатам расчета. Как вы можете заметить, они немного отличаются. Расчетные более точные, в том числе и потому, что указывается реальная плотность частиц, полученная в результате лабораторных исследований.

Выводы
В статье были предложены некоторые варианты для поиска и интерполяции значений. Конечно, их гораздо больше. Но уже с помощью этой информации вы самостоятельно сможете интерполировать любые таблицы или значения, которые найдете в нормативной документации или полученные в результате исследований. Без использования специального программного обеспечения, созданного для целей обработки геологической информации, можно вполне обойтись MS Office Excel.
Самый наглядный способ демонстрации динамики изменения данных в таблице - график. Информация в таком виде воспринимается легче табличной. В данной статье мы на примерах разберём несколько простейших способов построения графиков в Excel. С одним и несколькими рядами данных.
Для создания графика в программе MS Excel на основе таблицы с данными воспользуемся разделом Диаграммы на вкладке Вставка ленты инструментов. Разберём подробно инструменты: График и Точечная. Эти виды диаграмм соответствуют привычным математическим графикам.

Диаграмма типа График
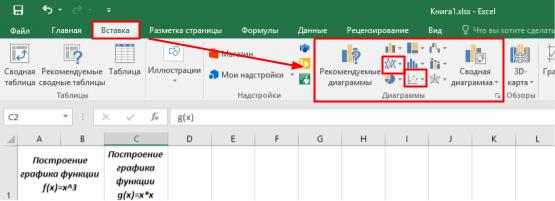
Для построений необходимо выделить столбец, содержащий значения функции, вместе с заголовком и выполнить команду вкладка Вставка — инструмент График. Выбираем вариант График с маркерами как наиболее показательный.
После нажатия на пиктограмму получаем график функции, который необходимо доработать по следующим позициям:
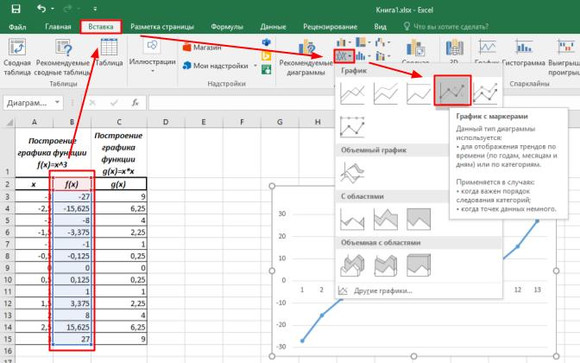
Внесëм необходимые изменения при помощи раздела Работа с диаграммами и двух его вкладок Конструктор и Формат. Он становится доступным при выделенной диаграмме. Также справа от диаграммы появляются три дополнительных инструмента: элементы, стили и фильтры. Они помогают облегчить работу по редактированию графика.
Добавить подписи и легенду можно двумя способами:
- с помощью инструмента Экспресс макеты на вкладке Конструктор;
- воспользоваться инструментом Элементы диаграммы (значок + в правом верхнем углу), расставив необходимые флажки.
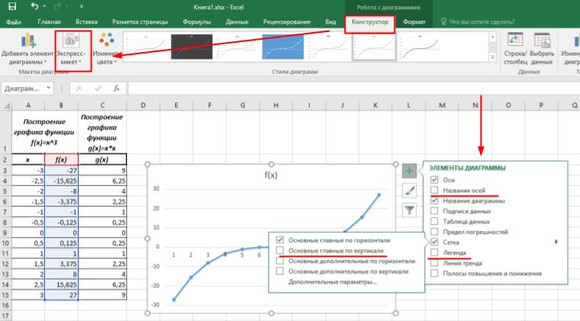
Заполняем поля подписей осей. Щелчком правой кнопки мыши (ПКМ) на поле надписи вызываем контекстное меню и выбираем пункт Изменить текст. Вводим данные с клавиатуры или копируем из соответствующих ячеек таблицы.
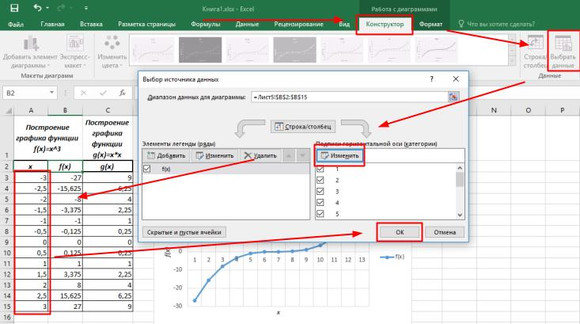
Изменяем значения горизонтальной оси таким образом, чтобы они соответствовали табличным. На вкладке Конструктор выбираем инструмент Выбрать данные. В диалоговом окне в графе Подписи горизонтальной оси нажимаем кнопку Изменить. Выделяем столбец, содержащий данные аргумента функции, без заголовка и дважды нажимаем на кнопку ОК.
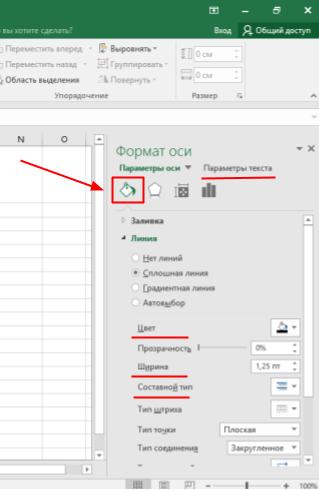
Последним шагом в оформлении графика будет форматирование осей. Шаг необязательный, но после него оси абсцисс и ординат станут заметнее выделяться на сетке. Это сделает график более наглядным.
Левой кнопкой мыши (ЛКМ) выделяем горизонтальную ось и переходим на вкладку Формат. Инструмент Формат выделенного объекта вызывает диалоговое окно форматирования в правой части программы.
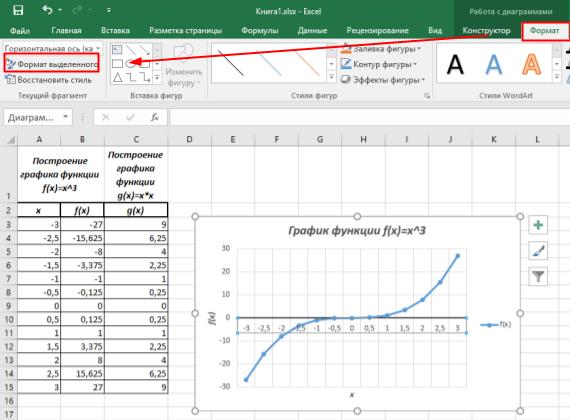
В разделе Заливка и границы изменяем параметры для линии: цвет, ширина, тип. Также, если есть необходимость, прорабатываем параметры текста в том же окне.
Добавление линии на график
Добавим к построенному графику ещё одну функцию. Для этого одним щелчком ЛКМ выделяем график и на вкладке Конструктор выбираем инструмент Выбрать данные. В диалоговом окне в графе Элементы легенды нажимаем кнопку Добавить.
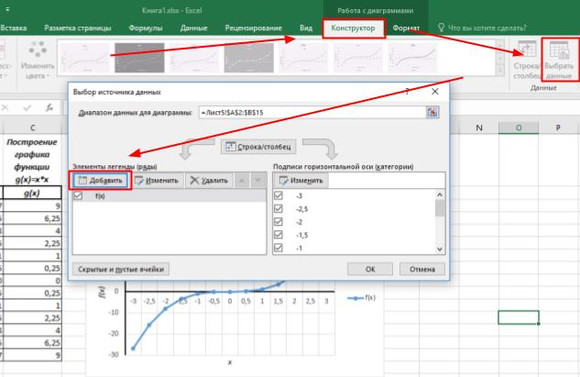
Заполняем диалоговое окно Изменение ряда. В поле Имя ряда вносим ячейку, содержащую название функции. В поле Значения — диапазон значений функции. Дважды нажимаем кнопку ОК.
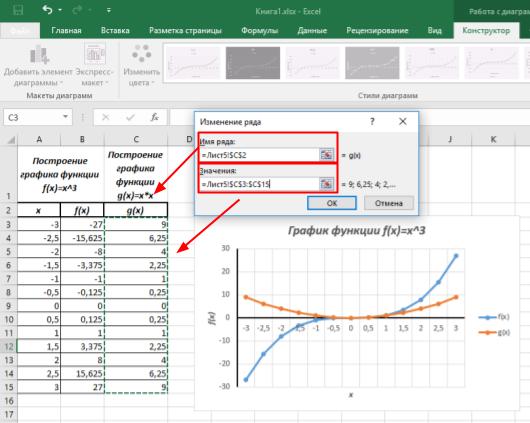
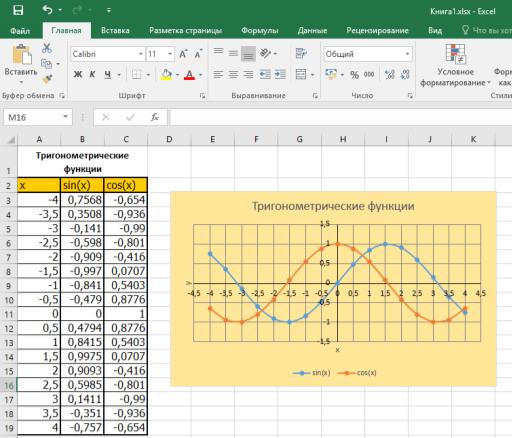
Диаграмма типа Точечная
Для построений необходимо выделить всю таблицу вместе с заголовком и выполнить команду вкладка Вставка — инструмент Точечная. Выбираем вариант Точечная с гладкими кривыми и маркерами как более показательный.
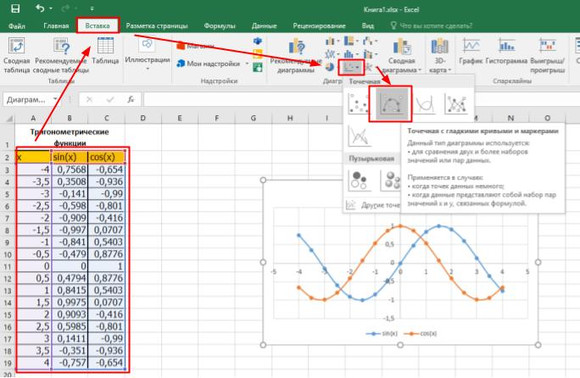
После нажатия на пиктограмму получаем график функций. Самым большим преимуществом точечной диаграммы является автоматическая подпись горизонтальной оси и ось ординат, которая располагается в точке 0. Как и в варианте “график”, данную диаграмму надо доработать:
- добавить подписи осей и названия диаграммы;
- добавить или изменить легенду (название функций);
- оформить оси (по необходимости).
Для этого, также как и в случае с графиком, используются раздел Работа с диаграммами и вкладки Конструктор и Формат. А также дополнительные инструменты справа от диаграммы: элементы, стили и фильтры.
Добавляем подписи и легенду с помощью инструмента Экспресс макеты на вкладке Конструктор или воспользовавшись инструментом Элементы диаграммы (значок + справа от диаграммы), расставив необходимые флажки.
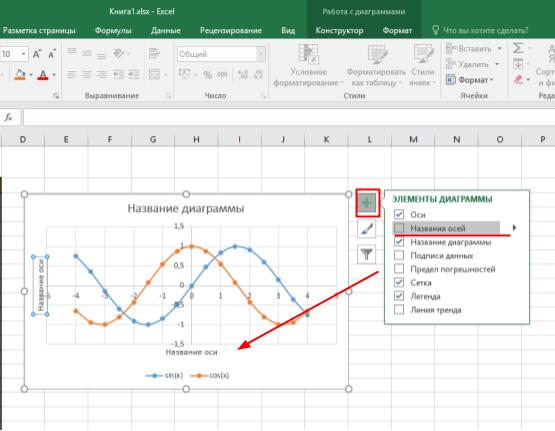
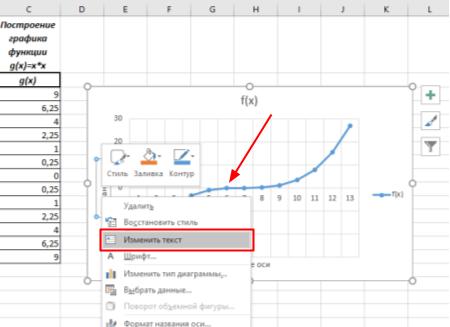
Поля подписей заполняем аналогично предыдущему графику: щелчок ПКМ по полю надписи — Изменить текст или двойной щелчок ЛКМ. Данные заполняем с клавиатуры или путём копирования из соответствующих ячеек.
Последним штрихом придаём графику больше наглядности — форматируем оси. Левой кнопкой мыши выделяем горизонтальную ось и переходим на вкладку Формат. Инструмент Формат выделенного объекта вызывает окно форматирования в правой части программы.
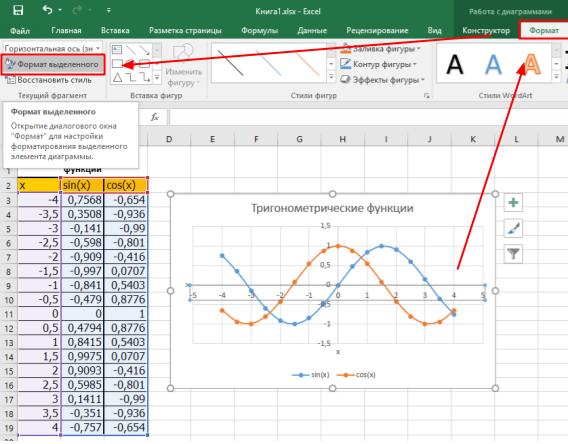
В разделе Заливка и границы изменяем параметры для линии тем же способом как при форматировании графика.
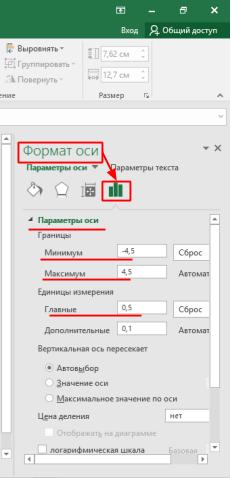
Следующим шагом ограничим ось абсцисс. В разделе Параметры оси изменяем максимальную и минимальную границы на 4,5 и - 4,5 соответственно. Уменьшаем шаг с 1 до 0,5 в разделе Единицы измерения для более наглядного отображения данных.
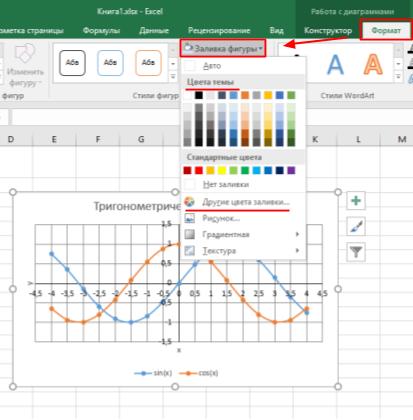
Последним штрихом в работе с графиком функции может быть изменение заливки области диаграммы. Для этого на вкладке Формат выбираем инструмент Заливка фигуры и устанавливаем необходимый цвет заливки.
В итоге преобразований получаем следующую диаграмму типа точечная.
Спасибо за Вашу оценку. Если хотите, чтобы Ваше имя
стало известно автору, войдите на сайт как пользователь
и нажмите Спасибо еще раз. Ваше имя появится на этой стрнице.

Понравился материал?
Хотите прочитать позже?
Сохраните на своей стене и
поделитесь с друзьями
Вы можете разместить на своём сайте анонс статьи со ссылкой на её полный текст

Ошибка в тексте? Мы очень сожалеем,
что допустили ее. Пожалуйста, выделите ее
и нажмите на клавиатуре CTRL + ENTER.
Читайте также:


