Почему при компьютерной обработке и передаче данных электронные данные представлены в битах
Данные могут быть представлены в аналоговой или цифровой форме. Компьютеры используют цифровую форму для хранения информации. Поэтому данные должны быть преобразованы в цифровую форму, чтобы их можно было использовать на компьютере.
Цифро-цифровое кодирование
Цифро-цифровое кодирование - это представление цифровой информации цифровым сигналом. Когда двоичные 1 и 0, генерируемые компьютером, преобразуются в последовательность импульсов напряжения, которые могут распространяться по проводам, этот процесс называется цифро-цифровым кодированием.
Цифро-цифровое кодирование делится на три категории:
- Униполярное кодирование
- Полярное кодирование
- Биполярное кодирование
Униполярный
- Цифровая система передачи посылает импульсы напряжения по средней линии связи, такой как провод или кабель.
- В большинстве типов кодирования один уровень напряжения представляет 0, а другой уровень напряжения представляет 1.
- Полярность каждого импульса определяет, является ли он положительным или отрицательным.
- Этот тип кодирования известен как униполярное кодирование, поскольку он использует только одну полярность.
- В униполярном кодировании полярность назначается двоичному состоянию 1.
- В этом 1 представлены как положительное значение, а 0 представлены как нулевое значение.
- В униполярном кодировании «1» рассматривается как высокое напряжение, а «0» - как нулевое напряжение.
- Униполярное кодирование проще и дешевле в реализации.
У униполярного кодирования есть две проблемы, которые делают эту схему менее желательной:
- Компонент постоянного тока
- Синхронизация
Полярное
- Полярное кодирование - это схема кодирования, которая использует два уровня напряжения: один положительный, а другой отрицательный.
- Используя два уровня напряжения, средний уровень напряжения уменьшается, и проблема компонента постоянного тока схемы униполярного кодирования облегчается.
NRZ означает невозвратный ноль.
В кодировании NRZ уровень сигнала может быть представлен как положительным, так и отрицательным.
Два наиболее распространенных метода, используемых в NRZ:
NRZ-L: в кодировании NRZ-L уровень сигнала зависит от типа бита, который он представляет. Если бит равен 0 или 1, то их напряжения будут положительными и отрицательными соответственно. Следовательно, можно сказать, что уровень сигнала зависит от состояния бита.
NRZ-I: NRZ-I является инверсией уровня напряжения, который представляет 1 бит. В схеме кодирования NRZ-I происходит переход между положительным и отрицательным напряжением, которое представляет 1 бит. В этой схеме 0 бит представляет отсутствие изменений, а 1 бит представляет изменение уровня напряжения.
RZ расшифровывается как Return to zero.
Для достижения синхронизации должно быть изменение сигнала для каждого бита. Однако для изменения каждого бита нам нужно иметь три значения: положительное, отрицательное и ноль.
RZ - это схема кодирования, которая предоставляет три значения, положительное напряжение представляет 1, отрицательное напряжение представляет 0, а нулевое напряжение не представляет ничего.
В схеме RZ, в середине каждого интервала, сигнал возвращается к нулю.
В схеме RZ 1 бит представлен положительным нулем, а 0 бит представлен отрицательным нулем.
Недостаток РЗ:
Он выполняет два изменения сигнала для кодирования одного бита, который получает большую полосу пропускания.
Двухфазный
Это схема кодирования, в которой сигнал изменяется в середине битового интервала, но не возвращается к нулю.
Двухфазное кодирование реализуется двумя различными способами:
- Он изменяет сигнал в середине битового интервала, но не возвращается к нулю для синхронизации.
- В манчестерском кодировании переход с отрицательного на положительный представляет двоичный 1, а с положительного на отрицательный - 0.
- Манчестер имеет тот же уровень синхронизации, что и схема RZ, за исключением того, что он имеет два уровня амплитуды.
Дифференциальный Манчестер
- Он изменяет сигнал в середине интервала битов для синхронизации, но наличие или отсутствие перехода в начале интервала определяет бит. Переход означает двоичный 0, а не переход означает двоичный 1.
- В схеме манчестерского кодирования два изменения сигнала представляют 0, а одно изменение сигнала представляет 1.
Биполярный
Схема биполярного кодирования представляет три уровня напряжения: положительный, отрицательный и нулевой.
В данной схеме нулевой уровень представляет двоичный 0, а двоичный 1 представлен переменным положительным и отрицательным напряжениями.
Если первый 1 бит представлен положительной амплитудой, то второй 1 бит представлен отрицательным напряжением, третий 1 бит представлен положительной амплитудой и так далее. Это чередование также может происходить, даже если 1 бит не является последовательным.
Биполярный может быть классифицирован как:
AMI означает альтернативную инверсию метки, где работа с метками происходит из телеграфии, что означает 1. Таким образом, она может быть переопределена как альтернативная инверсия 1 .
В схеме биполярного кодирования AMI, 0 бит представлен нулевым уровнем, а 1 бит представлен переменным положительным и отрицательным напряжениями.
Преимущество:
- Компонент постоянного тока равен нулю.
- Последовательность битов 1 с синхронизируется.
Эта схема кодирования не обеспечивает синхронизацию длинной строки битов 0 с.
Данный метод принят в Северной Америке для обеспечения синхронизации длинной последовательности битов 0 с.
В большинстве случаев функциональность B8ZS аналогична биполярному AMI, но единственное отличие состоит в том, что он обеспечивает синхронизацию, когда возникает длинная последовательность битов 0 с.
B8ZS обеспечивает синхронизацию длинной строки 0 с помощью принудительного искусственного изменения сигнала, называемого нарушениями, в пределах последовательности 0 строк.
Когда приходит сигнал восьми 0, тогда B8ZS реализует некоторые изменения в строковом шаблоне 0 с, основываясь на полярности предыдущего 1 бита.
Если полярность предыдущего 1 бита положительна, восемь 0 будут закодированы как ноль, ноль, ноль, положительный, отрицательный, ноль, отрицательный, положительный.
Компьютеры представляют данные, используя «0» и «1», которые также известны как двоичныечисла. Почему компьютеры используют двоичную запись вместо более близкой людям десятичной системы (в которой используются цифры 0-9)? Каждая цифра, двоичная она или десятичная, представляется напряжением в схеме компьютера. Сравнительно просто, сформировать схемы, выделяя два напряжения. Мы можем называть эти напряжения "включено" и "выключено". Намного более тяжело, хотя и не невозможно, сформировать схемы, которые бы были способны надежно различать десять различных напряжений.
- Parsons/Oja, Chapter 1-Section C.Цель обучения:Знание основных компонентов аппаратного обеспечения компьютера и двоичного представления.
Биты и байты
- Представление данных с помощью двоичных цифр
- Увеличение необходимости в Байтах Увеличение потребности в компьютерной памяти
Представление данных, используя двоичное исчисление
Порция данных, например, буква алфавита, может быть представлена, используя последовательность двоичных символов – «0» и «1». Есть несколько видов кодов, используемых, чтобы представить символьные данные – (character data). Например, используя расширенный код ASCII (Американский Стандартный Код для Информационного Обмена), буква алфавита "a" может быть представлена, используя последовательность восьми двоичных разрядов "01100001". Каждый двоичный разряд называется бит. А восемь бит – это один байт. Расширенный код ASCII использует восемь бит (или один байт), чтобы представить входные символы. Ниже показаны двоичные представления символов в расширенном коде ASCII.

Рисунок 1 Код ASCII
Все данные, в том числе звуковые, визуальные и программы могут быть представлены и сохранены, используя последовательность двоичных чисел или последовательность байтов. Иначе говоря – файл это коллекция данных. В некоторых файлах биты данных непосредственно кодируют индивидуальные буквы, номера и символы пунктуации, которые формируют слова и предложения. В других файлах, например файлах изображениях, биты данных должны быть пересчитаны для преобразования в изображения, которые мы сможем воспринимать.
Большинство приложений, например Microsoft Word или PowerPoint кодируют информацию специальными способами, не для чтения человеком. Поэтому, хотя Microsoft Word часто используется для редактирования текста, документ Word не может правильно отображен простым текстовым редактором, таким как Notepad, в связи с тем, что документ включает информацию в формате специфическом для Microsoft Word. По этой причине, чтобы его прочитать, его нужно открывать в Microsoft Word. Некоторые файлы имеют заголовок, указывающий на то какой формат использовался для кодирования данных, чтобы дать возможность компьютеру повторно собрать двоичные данные обратно в удобочитаемую форму документа.
Увеличение потребности в компьютерной памяти
В конце 1970-х и начале 1980-х, начали производиться недорогие персональные компьютеры, и вскоре вырос большой потребительский рынок. Вначале хватало, небольших объемов памяти, таких как тысячи байтов, чтобы обработать простую электронную таблицу и тексты. Но позже пользователи пожелали программное обеспечение, позволяющее им выполнить больше задач, таких как рисование и макетирование страниц. Пользовательские запросы возросли, соответственно росли требования к вычислительным возможностям. Этот спрос приводил к новому развитию, которое требовало расширения памяти. В середине 1980-х память выросла до миллионов байтов. Сегодня у офисных и домашних компьютеров миллиарды и даже больше байтов памяти. Потребности в памяти для систем, использующих данные интенсивно, таких как, например, Geographic Information System (GIS) (Географическая Информационная Система), составляет триллионы байтов. Ниже — диаграмма, иллюстрирующая емкости запоминающих устройств, начиная с 1970-х с соответствующими префиксами и аббревиатурами.
| 1970-е | 1980-е | 1990-е | 2000-е | |
| Порядок величины объема памяти в байтах | тысячи | миллион | биллион | триллион |
| Префикс | Kilo (10 3 ) | Mega (10 6 ) | Giga (10 9 ) | Tera (10 12 ) |
| Аббревиатура | K | M | G | T |
Что касается памяти то, чем больше, тем лучше. Другими словами, больше информации в форме данных и программ, которые их обрабатывают, может быть сохранено в памяти компьютера. Соответственно с ростом ёмкости устройств хранения, объёмы памяти также возрастают. Более того, технологии производства компьютерной памяти дают более компактные, легкие и быстрые устройства за туже цену. Вы узнаете больше о памяти и технологиях памяти в следующем модуле этого курса.
Системы счисления
- Десятичная
- Двоичная
- Шестнадцатиричная
- Упражнение
Мир вычислений использует несколько систем счисления для представления данных. Пока десятичная система, также известная как система счисления с основанием 10 (base10), ближе людям, так как это – система счисления, используемая в быту, двоичная (base2) и шестнадцатиричная (base16) — основные системы счисления используемые в вычислениях.
Мы начнем обсуждение систем счисления с рассмотрения десятичной системы как примера позиционной системы счисления. Десятичная система счисления содержит десять значений — 0, 1, 2, 3, 4, 5, 6, 7, 8, и 9. Каждое число в десятичной системе счисления может быть разбито на цифры по их "порядку" (позиции) в числе. Рассмотрим, например, число 43,872, где 2 находится на его 0-й позиции, 7 находится на его первой, 8 — на второй, 3 — на третьей, и 4 — на четвертой позиции. Каждая позиция имеет значение, которое может быть представлено либо экспоненциальным, либо десятичным значением. Следующая таблица показывает экспоненциальное и десятичное представление для каждой позиции числа 43,872.
| Порядок | 4-е | 3-е | 2-е | 1-е | 0-е |
| Цифра | |||||
| Экспоненциальное значение порядка | 10 4 | 10 3 | 10 2 | 10 1 | 10 0 |
| Десятичное значение порядка | 10,000 | 1,000 |
Таблица 1. Экспоненциальное и десятичное соответствие позиции цифры в числе
Отметим, что экспоненциальные значения увеличиваются соответственно позиции цифры. Например, экспоненциальное значение 4-й позиции составляет 10 4 .
Чтобы определить значение числа, перемножают цифру в столбце со значением, которое представляет столбец. Следующая запись - простое вычисление для предыдущего примера.
4 × 10 4 + 3 × 10 3 + 8 × 10 2 + 7 × 10 1 + 2 × 10 0 =
4 × 10,000 + 3 × 1000 + 8 × 100 + 7 × 10 + 2 × 1 =
40,000 + 3000 + 800 + 70 + 2 =
43,872
Хотя выполнение этих вычислений на десятичных числах кажется тривиальным, это демонстрирует образец, или формулу, которая может использоваться для конвертации числа из любой системы счисления к десятичной. Иначе говоря,
Где p — позиция, b — основание системы счисления, dp — цифра на самой высокой позиции в числе, dp-1 — следующая позиция в числе и так далее.
Используя пример числа, рассмотренный ранее, получим dp = 4, dp-1 = 3, b = 10, и p = 4.
4 × 10 4 + 3 × 10 3 + 8 × 10 2 + 7 × 10 1 + 2 × 10 0 = 43,872
Формулу, приведенную выше, можно использовать для расчетов десятичного числового значения любого числа в заданной базе. Ниже показан пример расчета для конвертации числа 214 (основание системы счисления 4) в десятичное значение.
| Позиция | 1st | 0th |
| Цифра | ||
| Экспоненциальное значение позиции | 4 1 | 4 0 |
| Десятичное значение позиции |
Таблица 2. Экспоненциальное и десятичное значения позиции цифр в числе
2(4) 1 + 1(4) 0 =
2× 4 + 1 × 1 =
8 + 1 =
9
До сих пор мы обсуждали преобразование чисел в десятичные. Важно также уметь конвертировать числа из десятичной в другие системы счисления. Используя систему base4, сконвертируем число 89 из десятичной формы в число с основанием системы счисления 4 (base4).
Сначала, найдем значение p, где 4 p < = 89 < 4 p+1 . В этом случае case p = 3. p — номер наивысшей позиции.
Теперь заполним следующую таблицу:
| Позиция | ||||
| Экспоненциальное значение порядка | 4 3 | 4 2 | 4 1 | 4 0 |
| Десятичное значение порядка | ||||
| Вычисление | 89 ÷ 64 | 25 ÷ 16 | 9 ÷ 4 | 1 ÷ 1 |
| Результат | ||||
| Остаток |
Таблица 3. Преобразование чисел из системы base10 в base4
Теперь рассмотрим двоичную и шестнадцатиричную систему более подробно.
Поскольку все системы счисления преобразуются одинаково, вы уже имеете все необходимое, чтобы преобразовывать число в двоичный код и обратно. Давайте рассмотрим преобразование из двоичного в десятичное числа, которое в двоичной форме записывается как 10110110.
Наивысшая позиция p, получена подсчетом числа позиций в двоичном коде, начиная с нуля.
1 × 2 7 + 0 × 2 6 + 1 × 2 5 + 1 × 2 4 + 0 × 2 3 + 1 × 2 2 + 1 × 2 1 + 0 × 2 0 =
1 × 128 + 0 × 64 + 1 × 32 + 1 × 16 + 0 × 8 + 1 × 4 + 1 × 2 + 0 × 1 =
128 + 0 + 32 + 16 + 0 + 4 + 2 + 0 =
182
Например, в числе 100110 наибольшая позиция — 2 p , где p = 5. Поскольку двоичная система самая простая система счисления для преобразования в десятичную, она поможет нам позже, когда мы будем преобразовывать шестнадцатиричные числа.
Обратите внимание, что двоичная система использует больше цифр для выражения значения числа чем десятичная. Например, число 99 — в десятичном виде это 1100011 — в двоичном виде. Компьютерные профессионалы заимствовали шестнадцатиричное представление как стенографию для двоичного, чтобы представить двоичные значения в краткой форме.
Шестнадцатиричная (base16), по всей вероятности та система счисления, с которой вы будете работать. В современной десятичной системе набор арабских цифр 0-9 необходимо дополнить дополнительными значениями для представления десятичных эквивалентов — 10, 11, 12, 13, 14, и 15. Вместо изобретения новых символов для представления этих чисел, используются буквы A-F. Шестнадцатиричная система представляется набором цифр 0-F. Используются как буквы нижнего, так и верхнего регистра (большие и маленькие). В этом курсе мы будем использовать верхний регистр A-F. Шестнадцатиричный формат, однако, обычно не представляется добавлением индекса 16 к цифре обозначающей число. Вместо этого используются два различных формата для представления шестнадцатиричных чисел: с добавлением вначале 0x или с добавлением в конце h. Мы будем использовать 0x, чтобы обозначать шестнадцатиричные числа.
| Позиция | |||||
| Экспоненциальное значение позиции | 16 4 | 16 3 | 16 2 | 16 1 | 16 0 |
| Десятичное значение позиции | 65,536 |
Таблица 4. Экспоненциальное и десятичное представление цифровой позиции числа
Есть два метода преобразования шестнадцатиричного числа в десятичное. При прямом преобразовании используется следующая формула
Где dp – цифра на самой высокой позиции в числе, и dp-1 — следующая цифра на следующей позиции и так далее. b — база и p — значение самой высокой позиции.
Преобразование выглядит так:
4 × 16 3 + A × 16 2 + 3 × 16 1 + F × 16 0 =
4 × 4096 + 10 × 256 + 3 × 16 + 15 × 1 =
16,384 + 2560 + 48 + 15 =
19,007
Этот метод особенно полезен для больших шестнадцатиричных чисел. Однако, для небольших чисел из одной или двух цифр, часто быстрее преобразовать шестнадцатиричное число в двоичное перед превращением его в десятичное. Шестнадцатиричный формат поддерживает связь с двоичным, так как он – производный от системы base2. Каждая шестнадцатиричная цифра представляет четыре двоичных разряда. Таблица ниже показывает взаимосвязь между двоичным, шестнадцатиричным, и десятичным форматами для 0x0-0xF.
| Десятичный | Двоичный | Шестнадцатиричный |
| 0x0 | ||
| 0x1 | ||
| 0x2 | ||
| 0x3 | ||
| 0x4 | ||
| 0x5 | ||
| 0x6 | ||
| 0x7 | ||
| 0x8 | ||
| 0x9 | ||
| 0xA | ||
| 0xB | ||
| 0xC | ||
| 0xD | ||
| 0xE | ||
| 0xF |
Таблица 5. Десятичные, двоичные и шестнадцатиричные преобразования
Давайте преобразуем 0x3B к десятичному виду через двоичный. Первый шаг – выяснить, что отдельное шестнадцатиричное число представляет собой в двоичном виде. Заменим шестнадцатиричное число двоичным числом. Так, 0x3B становится 00111011. Как вы помните из предыдущего раздела о двоичном счислении, преобразование числа от двоичного к десятичному намного проще, чем в другие системы, поскольку умножение двоичных разрядов на 0 и 1 — простая операция.
0x3B=
001110112=
32 + 16 + 8 + 2 + 1 =
59
Байт данных (восемь битов) может быть записан в виде двух шестнадцатиричных цифр. Например, символ "N" в расширенном коде ASCII имеет двоичное представление 01001110. Если мы записываем его как две группы из четырех битов каждый, мы получаем 0100.1110. Используя таблицу 5 (выше), мы находим, что 0100 составляет 0x4 и 1110 — 0xE. Поэтому, соответствующий шестнадцатиричный для 0100.1110 есть 0x4E.
Вы можете поэкспериментировать с преобразованиями между двоичным, десятичным и шестнадцатиричным представлениями, используя приложение Microsoft Calculator.
Передача данных — процесс переноса данных в виде сигналов от точки к точке или от точки к нескольким точкам средствами электросвязи по каналу. Словари упоминают заимствование (1640-е) учеными кругами латинского слова datum, означающего «вещь», «данность». Философия обосновывает связь понятий информации, знания, данных, свободы, приводит примеры. Высота горы преимущественно выступает данными. Параметр измеряют альтиметром, заполняют базы. Полученная информация, приняв конкретный облик, украшает книгу, изучаемую альпинистом. Бывалый горец придумывает лучший способ покорить вершину. Понимание особенностей процесса уже становится знанием.
Немедля появляется свобода выбора. Альпинист волен решать, принимая ответственность. Имеются группы, не вернувшиеся назад.
Виды данных

Аналоговый сигнал
Первыми попытками измерить аналоговые величины назовем опыты Вольты, измерявшего напряжение, ток. Следом сопротивление проводника сумел оценить Ом, Георг Ом. Каждый раз использовались аналоговые величины. Представление характеристик объекта в виде тока, напряжения дало мощный толчок развития современному миру. Электронно-лучевой кинескоп яркостью пикселей трех цветов отображает достаточно наглядную картинку.
Причины ухода от аналогового сигнала выявила Вторая мировая война. Система Зеленый шершень умела отлично шифровать информацию. 6-уровневый сигнал сложно назвать цифровым, однако намечается явный уклон. Исторически первой попыткой передачи бинарного кода назовем опыты Шиллинга 1832 года с телеграфом. Стремясь снизить количество соединяющих абонентов проводов, дипломат припомнил предложенные священниками методики двоичного счисления. Однако внедрение цифровой передачи потребовало от человечества пройти путь свыше полутора столетий.
Двоичный цифровой код
Двоичное счисление общеизвестно. Аналоговую величину представляют дискретным числом, затем производят кодирование. Полученный набор нулей, единиц обычно разбивают словами длиной 8 бит. Так, например, первые операционные системы Windows были 16-битными, графический модуль процессора обрабатывал числа с плавающей запятой разрядностью повыше. Еще более длинные слова используют специализированные вычислители графических карт. Специфика системы определяет конкретный способ представления информации.
Передача данных позволяет человечеству идти вперед быстрее. Люди обладают неодинаковыми способностями. Необязательно лучший сборщик, хранитель информации сможет извлечь выгоду (для себя, планеты, города…). Разумнее передать. Современный мир называют эпохой цифровой революции. Исторически оказалось, что двоичные данные передавать проще, появляется набор специфических возможностей:
- Исправление ошибок.
- Шифрование.
- Упрощение физических линий.
- Более эффективное использование спектра, снижение мощности передатчика, удельной плотности потока энергии.
- Распознавание ошибок (EDC, 1951).
- Возможность точного повтора, воспроизведения.
Вторая половина XX века дала сотни методик оцифровки аналоговых объектов. Главным признаком двоичного сигнала является дискретность. Аналоговую величину доподлинно передать код бессилен. Однако шаг дискретизации стал столь малым, что погрешностью пренебрегают. Яркий пример – изображения формата Full HD. Большое разрешение экрана гораздо лучше передает мелкие нюансы объекта. На некотором этапе разрешение цифровой техники обгоняет физиологические возможности человеческого зрения.
Значения термина
- Передача сведений.
- Компьютерная программа для Windows Phone, обеспечивающая копирование контактов меж мобильными устройствами.
- Научно-популярная программа с Марией Бачениной.

Этиология
Англичанами принято употреблять множественное число – data. Славянофилов просим избегнуть упреков. Современная наука развита Европой – наследницей Римской империи. Вопрос намеренного уничтожения отечественной истории обойдем, оставив прения историкам. Некоторые эксперты возводят этимологию к древнему индийскому слову dati (дар). Даль называет данными бесспорные, очевидные, известные факты произвольного толка.
Это интересно! Литературный английский язык (газета Нью-Йорк таймс) слово data лишает числа. Употребляют как придется: множественное, единственное. Учебники чаще проводят жесткое деление. Единственное число – datum. Отдельный вопрос касается артикля, здесь обсуждаться не будет. Эксперты склонны считать существительное «массовым».
Идея открытости
Идея свободного доступа к информации выдвинута отцом социологии, Робертом Кингом Мертоном, наблюдавшим Вторую мировую войну. Начиная 1946 годом, подразумевает передачу, хранение компьютерной информации. 1954 добавил возможность обработки. В декабре 2007 года желающие обсудить проблему собрались (Себастопол, Калифорния) и осмыслили программное обеспечение с открытым кодом, интернет, потенциал концепции массового доступа. Обама принял Меморандум о прозрачности и открытости действий правительства.

Осознание человечеством реального потенциала цивилизации сопровождается призывами совместно решать проблемы. Концепция открытости данных широко обсуждается документом (1995) Американского научного агентства. Текст затрагивает геофизику и экологию. Общеизвестен пример корпорации ДюПонт, использовавший некоторые спорные технологии производства Тефлона.
Термины
Термин передача данных чаще касается цифровой информации, включая преобразованный аналоговый сигнал. Наука смотрит шире. Данными именуют любые качественные, количественные описания объекта. Эпичным примером считают сведения, составляемые антропологами касательно редких народностей планеты. Информация широко собирается организациями: продажи, преступность, безработица, грамотность.
Передача информации – цифровой поток бит.
Метаданные – более высокий уровень данных, описывающих другие данные.
Данные измеряют, собирают, передают, анализируют, представляют графиками, таблицами, изображениями, цифрами. Программистам известны так называемые рядовые файлы, лишенные форматирования. Сбойный раздел жесткого диска получает метку RAW. Форматирование упрощает передачу, восприятие сведений. Процесс оформления касается визуального, логического представления. Иногда информацию кодируют, обеспечивая защиту, восстановление сбойных участков.
Формат – способ представления информации.
Протокол – набор соглашений интерфейса, определяющий порядок обмена информацией.
Каналы (способы)
Информация, распространяясь, преодолевает среду:
- Медный кабель: RS-232 (1969), FireWire (1995), USB (1996).
- Оптическое волокно.
- Эфир (беспроводная передача).
- Шины компьютера.
Специфика среды накладывает особенности. Немногим известно, что электрический ток разносится также электромагнитной волной. Проводимость воздуха намного ниже, что накладывает специфику. Разница нивелируется ионизацией – явлением, знакомым сварщикам. Процессы, сопровождающие движение электромагнитной волны, лишены научного объяснения. Физики просто констатируют факт, описывая явление набором сведений.
Долгое время разные частоты считали явлениями несвязными: свет, тепло, электричество, магнетизм. Важно понять: набор сред рожден эволюцией техники. Наверняка откроют иные методы передачи данных. Реализации сред различны, набор стандартов определен спецификой. Локальные соединения часто пользуются технологией WiFi, опирающейся на протокол канального уровня IEEE 802.11. Сотовые операторы применяют совершенно иные – GPS, LTE. Причем мобильные сети активно начинают внедрять IP, замыкая круг, унифицируя стиль использования цифрового оборудования.
Зачем много протоколов? Особенности реализации передачи данных через WiFi бессильны покрыть значительные расстояния. Лимитированы мощности передатчиков, структуры пакетов иные. Bluetooth вовсе ограничивает основные возможности передачей пары файлов с компьютера на телефон.
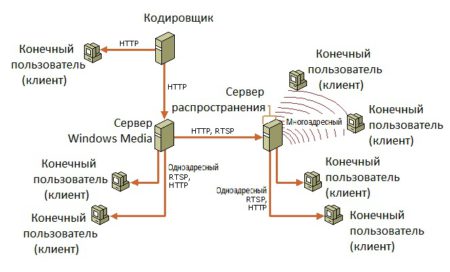
Форматирование
Основу сетей заложил американский ARPANET. С ПК на ПК стали передавать пакеты. Тогда в сети начали применяться первые цифровые протоколы. Сегодня IP захватывает сегмент мобильной связи. Телефоны получают собственные адреса.
Слои протоколов
Передача цифровых данных модемом реализована в 1940 году. Сети появились 25 лет спустя.

Концепция 7-слойной структуры представлена работами Чарльза Бэчмана. Модель OSI включает опыт разработки АRPANET, EIN, NPLNet, CYCLADES. Линейка полученных слоев взаимодействует по вертикали с соседями: верхний использует возможности нижнего.
Важно! Каждому уровню OSI соответствует набор протоколов, определяемый используемой системой.
В компьютерных линиях совокупность протоколов подразделяют на слои. Бывают:
Физический слой
Зачем разработчикам сто стандартов? Многие документы появились эволюционно, согласно возрастающим требованиям. Физический слой реализуют набором коннекторов, проводов, интерфейсов. Например, экранированная витая пара способна передавать высокие частоты, делая возможным реализацию протоколов битрейтом 100 Мбис/с. Оптоволокно пропускает свет, производится дальнейшее расширение спектра, возникают гигабитные сети.
Физический слой заведует схемами цифровой модуляции, физическим кодированием (формированием несущей, закладкой информации), опережающей коррекцией ошибок, синхронизацией, мультиплексированием каналов, выравниванием сигнала.
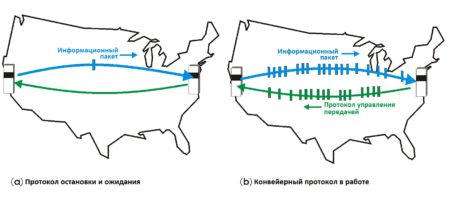
Канальный слой
Каждый порт управляется собственными машинными командами. Канальный слой показывает, как реализовать передачу форматированной информации, используя имеющееся железо. Например, PPPoЕ содержит рекомендации организации протокола PPP средствами сетей Ethernet, используемый традиционно порт – 8P8C. Эволюционной борьбой «эфирная сеть» смогла подавить соперников. Изобретатель концепции, основатель компании 3СОМ, Роберт Меткалф, сумел убедить несколько крупных производителей (Интел, DEC, Ксерокс) объединить усилия.
Попутно совершенствовались каналы: коаксиальный кабель → витая пара → оптическое волокно. Изменения преследовали цели:
- удешевления;
- повышения надежности;
- внедрения дуплексного режима;
- повышения помехоустойчивости;
- гальванической развязки;
- питания устройств посредством сетевого кабеля.
Оптический кабель повысил длину сегмента меж регенераторами сигнала. Канальный протокол больше описывает структуру сети, включая методы кодирования, битрейт, количество узлов, режим функционирования. Уровень вводит понятие кадра, реализует схемы расшифровки адреса MAC, детектирует ошибки, повторно отправляет запрос, контролирует частоту.
Сетевой
Общепринятый IP-протокол определяет структуру пакета, вводит специфический адрес из четырех групп цифр, известных сегодня каждому. Некоторые маски зарезервированы. Владельцам ресурсов присваиваются имена соответственно базам серверов DNS. Конфигурация сети во многом безразлична. Вводятся слабые ограничения. Как например, Ethernet требовал уникальности MAC-адреса. Протокол IP урезает максимальное число ПК 4,3 млрд штук. Человечеству пока что хватает.
Сетевой адрес принято делить на домены. По техническим причинам единое соответствие четырем группам цифр отсутствует. Сам интернет обозначает аббревиатура www (сокращенное название world wide web, иначе – всемирная паутина). Сегодня единообразный адрес (URL) опускает тривиальные буквы. Подразумевая – человек, открывший браузер, явно намеревается бороздить с компьютера всемирную паутину.
Транспортный
Слой далее расширяет структуру формата. Формирование сегмента TCP производит объединение пакетов, упрощая поиск потерявшейся информации, гарантируя восстановление.
Прикладной, представительский

Скорость последовательной передачи данных обычно обозначают термином битрейт (bit rate). Однако другой часто используемой единицей является скорость передачи в бодах (baud rate). Хотя это не одно и то же, при определенных обстоятельствах между обеими единицами существует определенное сходство. В статье дается четкое разъяснение различий между этими понятиями.
Общая информация
В большинстве случаев в сетях информация передается последовательно. Биты данных поочередно передаются по каналу связи, кабельному или беспроводному. На Рисунке 1 изображена последовательность бит, передаваемая компьютером или какой-либо другой цифровой схемой. Такой сигнал данных часто называют исходным. Данные представлены двумя уровнями напряжения, например, логической единице соответствует напряжение +3 В, а логическому нулю – +0.2 В. Могут использоваться и другие уровни. В формате кода без возврата к нулю (NRZ) (Рисунок 1) сигнал не возвращается к нейтральному положению после каждого бита, в отличие от формата с возвращением к нулю (RZ).
| Рисунок 1. | NRZ (без возврата к нулю) – наиболее распространенный формат двоичных данных. Скорость передачи данных измеряется в битах в секунду (бит/с). |
Битрейт
Скорость передачи данных R выражается в битах в секунду (бит/с или bps). Скорость является функцией продолжительности существования бита или времени бита (TB) (Рисунок 1):
Эту скорость называют также шириной канала и обозначают буквой C. Если время бита равно 10 нс, то скорость передачи данных определится как
R = 1/10 × 10 – 9 = 100 млн. бит/с
Обычно это записывается как 100 Мб/с.
Служебные биты
Битрейт, как правило, характеризует фактическую скорость передачи данных. Однако в большинстве последовательных протоколов данные являются только частью более сложного кадра или пакета, включающего в себя биты адреса источника, адреса получателя, обнаружения ошибок и коррекции кода, а также прочую информацию или биты управления. В кадре протокола данные называются полезной информацией (payload). Биты, не являющиеся данными, называются служебными (overhead). Иногда количество служебных бит может быть существенным – от 20% до 50%, в зависимости от общего числа полезных бит, передаваемых по каналу.
К примеру, кадр протокола Ethernet, в зависимости от количества полезных данных, может иметь до 1542 байт или октетов. Полезных данных может быть от 42 до 1500 октетов. При максимальном числе полезных октетов служебных будет только 42/1542, или 2.7%. Их было бы больше, если полезных байт было бы меньше. Это соотношение, известное также под названием эффективность протокола, обычно выражают в процентах количества полезных данных от максимального размера кадра:
Эффективность протокола = количество полезных данных/размер кадра = 1500/1542 = 0.9727 или 97.3%
Как правило, чтобы показать истинную скорость передачи данных по сети, фактическая скорость линии увеличивается на коэффициент, зависящий от количества служебной информации. В One Gigabit Ethernet фактическая скорость линии равна 1.25 Гб/с, тогда как скорость передачи полезных данных составляет 1 Гб/с. Для 10-Gbit/s Ethernet эти величины равны, соответственно, 10.3125 Гб/с и 10 Гб/с. При оценке скорости передачи данных по сети также могут использоваться такие понятия, как пропускная способность, скорость передачи полезных данных или эффективная скорость передачи данных.
Скорость передачи в бодах
Термин «бод» происходит от фамилии французского инженера Эмиля Бодо (Emile Baudot), который изобрел 5-битовый телетайпный код. Скорость передачи в бодах выражает количество изменений сигнала или символа за одну секунду. Символ – это одно из нескольких изменений напряжения, частоты или фазы.
Двоичный формат NRZ имеет два представляемых уровнями напряжения символа, по одному на каждый 0 или 1. В этом случае скорость передачи в бодах или скорость передачи символов – то же самое, что и битрейт. Однако на интервале передачи можно иметь более двух символов, в соответствии с чем на каждый символ отводится несколько бит. При этом данные по любому каналу связи могут передаваться только с помощью модуляции.
Когда средство передачи не может обработать исходный сигнал, на первый план выходит модуляция. Конечно, речь идет о беспроводных сетях. Исходные двоичные сигналы не могут передаваться непосредственно, они должны переноситься на несущую радиочастоту. В некоторых протоколах кабельной передачи данных также применяется модуляция, позволяющая повысить скорость передачи. Это называется «широкополосной передачей».
Выше: модулирующий сигнал, исходный сигнал
Используя составные символы, в каждом можно передавать по несколько бит. Например, если скорость передачи символов равна 4800 бод, и каждый символ состоит из двух бит, полная скорость передачи данных будет 9600 бит/с. Обычно количество символов представляется какой-либо степенью числа 2. Если N – количество бит в символе, то число требуемых символов будет S = 2N. Таким образом, полная скорость передачи данных:
R = скорость в бодах × log2S = скорость в бодах × 3.32 log10S
Если скорость в бодах равна 4800, и на символ отводится два бита, количество символов 22 = 4.
Тогда битрейт равен:
R = 4800 × 3.32log(4) = 4800 × 2 = 9600 бит/с
При одном символе на бит, как в случае с двоичным форматом NRZ, скорости передачи в битах и бодах совпадают.
Многоуровневая модуляция
Высокий битрейт можно обеспечить многими способами модуляции. Например, при частотной манипуляции (FSK) в каждом символьном интервале для представления логических 0 и 1 обычно используются две различные частоты. Здесь скорость передачи в битах равна скорости передачи в бодах. Но если каждый символ представляет два бита, то требуются четыре частоты (4FSK). В 4FSK скорость передачи в битах в два раза превышает скорость в бодах.
Еще одним распространенным примером является фазовая манипуляция (PSK). В двоичной PSK каждый символ представляет 0 или 1. Двоичному 0 соответствует 0°, а двоичной 1 – 180°. При одном бите на символ скорость в битах равна скорости в бодах. Однако соотношение числа бит и символов несложно увеличить (см. Таблицу 1).
Читайте также:


