Матрица которая получается из матрицы заменой строк столбцами называется по отношению к матрице

Обновлено: 24.01.2025

ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ

Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.

В общем виде матрицу размером m×n записывают так

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами a_ij: первый указывает номер строки, а второй – номер столбца. Например, a₂₃ – элемент стоит во 2-ой строке, 3-м столбце.

Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.

Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.

Различаются также матрицы, имеющие только одну строку или один столбец.

Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,

Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.

Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.

Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .

Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .

ДЕЙСТВИЯ НАД МАТРИЦАМИ

Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны a_ij = b_ij. Так если и , то A=B, если a₁₁ = b₁₁, a₁₂ = b₁₂, a₂₁ = b₂₁ и a₂₂ = b₂₂.

Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .

Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.

Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают A T .

Связь между матрицей A и её транспонированной можно записать в виде .

Например. Найти матрицу транспонированную данной.

Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,

Примеры. Найти сумму матриц:

.
- нельзя, т.к. размеры матриц различны.
.

Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).

Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .

Для любых чисел a и b и матриц A и B выполняются равенства:

.
Найти 2A-B, если , .

Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.

Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:

Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c₁₃, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.

В общем случае, если мы умножаем матрицу A = (a_ij) размера m×n на матрицу B = (b_ij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент c_ij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.

Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.

Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,

Найти элементы c₁₂, c₂₃ и c₂₁ матрицы C.

Найти АВ и ВА.

Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.

Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.

Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.

Например, если , то

ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ

Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .

Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a₁₁a₂₂ – a₁₂a₂₁.

Определитель обозначается символом .

Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.

Примеры. Вычислить определители второго порядка.

.
Вычислить определитель матрицы D, если D= -А+2В и

Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.

Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:

Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a₁₁, a₁₂, a₁₃ и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.

Примеры. Вычислить определитель третьего порядка.

(x+3)(4x-4-3x)+4(3x-4x+4)=0.

(x+3)(x-4)+4(-x+4)=0.

Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки "+" и "–" у слагаемых чередуются.

Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.

Пусть — произвольные матрицы, для которых определены операции умножения и сложения, записанные в левых частях следующих равенств. Тогда определены операции, указанные в правых частях, и справедливы равенства:

Пример 1.18. Найти транспонированные матрицы , если

Решение. Согласно определению, при транспонировании первая строка матрицы Аналогично находим

Так как — симметрическая.

Пример 1.19. Продемонстрировать справедливость свойств 1, 2, 3, 4, если

Решение. Продемонстрируем свойство 1: . Вычисляя левую и правую части, получаем равные матрицы

Продемонстрируем свойство 2: . Вычисляя левую и правую части, получаем равные матрицы

Продемонстрируем свойство 3: . Вычисляя левую и правую части, получаем равные матрицы:

Продемонстрируем свойство 4: . Вычисляя левую часть, получаем правую:

Пример 1.20. Пусть — симметрические, а матрица — кососимметрическая.

Решение. По свойствам 3,4 получаем:

Сопряжение матриц

Решение. Найдем транспонированные матрицы:

Заменим все элементы сопряженными:

Заметим, что матрица — эрмитова, так как .

Свойства операции сопряжения матриц

где — произвольные матрицы, для которых определены соответствующие операции, — любое комплексное число, — сопряженное к Пример 1.22. Продемонстрировать справедливость свойств 1, 2, 3, 4, если

Решение. 1. Вычисляем и сравниваем левую и правую части равенства 1:

2. Вычисляем и сравниваем левую и правую части равенства 2:

3. Вычисляем и сравниваем левую и правую части равенства

4. Вычисляем левую часть равенства 4 и сравниваем ее с правой частью:

Пример 1.23. Пусть — эрмитовы m-го и n-го порядков соответственно.

Решение. Используя свойства 3, 4, получаем:

что и требовалось доказать.

1. Эрмитова матрица с действительными элементами является симметрической.

След матрицы

Следом квадратной матрицы называется сумма ее элементов, стоящих на главной диагонали. След квадратной матрицы

Для любых квадратных матриц n-го порядка и столбцов размеров справедливы следующие свойства:

Замечание 1.6. След матрицы также обозначается .

Пример 1.24. Даны квадратные матрицы и столбцы . Продемонстрировать справедливость свойств 1, 2, 3, 4, 5, 7.

В математике транспонированная матрица , зеркальная матрица или инвертированная матрица - это матрица, которая создается путем обмена ролями строк и столбцов данной матрицы. Первая строка транспонированной матрицы соответствует первому столбцу выходной матрицы, вторая строка - второму столбцу и так далее. Транспонированная матрица явно создается путем отражения выходной матрицы по ее главной диагонали . Процесс преобразования матрицы в ее транспонированную матрицу называется транспонированием , транспонированием или переворачиванием матрицы.

Отображение транспозиции, которое назначает его транспонирование матрице, всегда биективно , линейно и самообратно . Что касается сложения матриц, это обеспечивает изоморфизм , но относительно умножения матриц это антиизоморфизм , то есть порядок умножения матриц меняется на противоположный путем транспонирования. Многие параметры матриц, такие как трек , ранг , определитель и собственные значения , сохраняются при транспонировании.

В линейной алгебре транспонированная матрица используется, среди прочего, для характеристики специальных классов матриц. Транспонированная матрица также отображение матрица с двойным отображением с линейным отображением между двумя конечномерными векторными пространствами относительно соответствующих двойных оснований . Кроме того, это также матрица отображения сопряженного отображения между двумя конечномерными пространствами вещественных скалярных произведений относительно соответствующих ортонормированных базисов . Концепция транспонирования матрицы была введена в 1858 году британским математиком Артуром Кэли .

определение

Если поле (на практике в основном поле действительных или комплексных чисел ), то она связана с данной матрицей K

транспонированная матрица, определяемая как

Примеры

Транспонирование матрицы ( вектора-строки ) создает матрицу ( вектор-столбец ) и наоборот: ( 1 × 3 ) ( 3 × 1 )

Квадратная матрица сохраняет свой тип за счет транспонирования , но все элементы отражаются на главной диагонали:

Путем транспонирования матрицы создается матрица, в которой первая строка соответствует первому столбцу выходной матрицы, а вторая строка соответствует второму столбцу выходной матрицы: ( 3 × 2 ) ( 2 × 3 )

характеристики

общее

Следующее применяется к транспонированию суммы двух матриц одного типа. А. знак равно ( а я j ) , Б. знак равно ( б я j ) ∈ K м × п ), \ B = (b_ ) \ in K ^ >

( А. + Б. ) Т знак равно ( ( а я j ) + ( б я j ) ) Т знак равно ( а я j + б я j ) Т знак равно ( а j я + б j я ) знак равно ( ( а j я ) + ( б j я ) ) знак равно А. Т + Б. Т > = ((a_ ) + (b_ )) ^ > = (a_ + b_ ) ^ > = (a_ + b_ ) = ((a_ ) + (b_ )) = A ^ > + B ^ >> .

Таким образом, транспонированная сумма матриц равна сумме транспонированных.

Скалярное умножение

Следующее применимо к транспонированию произведения матрицы со скаляром. А. знак равно ( а я j ) ∈ K м × п ) \ в К ^ > c ∈ K

Следовательно, транспонирование произведения матрицы на скаляр равно произведению скаляра на транспонированную матрицу.

Двойная транспозиция

Следующее применяется к транспонированию транспонирования матрицы. А. знак равно ( а я j ) ∈ K м × п ) \ в К ^ >

Таким образом, при двойном транспонировании выходная матрица всегда получается снова.

продукт

Следовательно, транспонирование произведения матриц равно произведению транспонированного произведения, но в обратном порядке.

Обратный

Транспонирование регулярной матрицы также является правильным. Следующее относится к транспонированию обратной регулярной матрицы. А. ∈ K п × п >

а значит и обратная матрица тоже . Таким образом, транспонированная обратная матрица равна обратной транспонированной матрице. Эта матрица иногда также обозначается как. ( А. - 1 ) Т ) ^ >> А. Т <\ Displaystyle А ^ >> А. - Т >

Экспонента и логарифм

Относится к в матрице экспоненты транспонированной реальной или комплексной квадратной матрицы А. ∈ K п × п ^ >

Соответственно, транспонирование регулярной вещественной или комплексной матрицы применяется к матричному логарифму

Отображение транспозиции

который назначает его транспонирование матрице, называется отображением транспонирования . Благодаря указанным выше законам отображение транспозиции имеет следующие свойства:

Блочные матрицы

Транспонирование блочной матрицы с разделами на строки и столбцы осуществляется через р s

дано. Он создается путем зеркального отображения всех блоков на главной диагонали и последующего транспонирования каждого блока.

Параметры

классифицировать

Для матрицы , то ранг транспонированной матрицы такой же , как и выходной матрицы: А. ∈ K м × п >

Изображение фигуры будет поддерживаться на векторах - столбцов из зажимает в то время как изображение изображения из векторов - строк из натянутых. В размеры этих двух фотографий всегда совпадают. Икс ↦ А. Икс А. Икс ↦ А. Т Икс > х> А.

отслеживать

Для квадратной матрицы , то след (сумма основных диагональных элементов ) транспонированной матрицы равен следу матрицы выходов: А. ∈ K п × п >

Это связано с тем, что диагональные элементы транспонированной матрицы совпадают с элементами выходной матрицы.

Детерминант

Для квадратной матрицы , то определитель транспонированной матрицы равен определителю матрицы выходов: А. ∈ K п × п >

спектр

Для квадратной матрицы из-за инвариантности определителя при транспонировании характеристический полином транспонированной матрицы также идентичен таковому для выходной матрицы: А. ∈ K п × п >

Следовательно, собственные значения транспонированной матрицы совпадают с собственными значениями выходной матрицы, поэтому два спектра совпадают:

сходство

Каждая квадратная матрица является похожа на транспонированном, то есть: существует регулярная матрица , такая , что А. ∈ K п × п > С. ∈ K п × п >

применяется. Матрицу можно даже выбрать симметричной . Из этого следует, среди прочего, что квадратная матрица и ее транспонированная матрица имеют одинаковый минимальный многочлен и, при условии, что ее характеристический многочлен полностью разделен на линейные множители , также имеют одинаковую жорданову нормальную форму . С.

Нормы

дано. Относится к в норме Фробениуса и спектральной нормы транспонированной реальной или комплексной матрицы А. ∈ K м × п > ^ >

Норма строки суммы и столбец сумма норма транспонированного и выходная матрица связаны следующим образом :

Скалярные произведения

дано. Что касается стандартного скалярного произведения, вещественная матрица и ее транспонирование обладают свойством смещения А. ∈ Р. м × п ^ >

ведь матрицы под дорожкой можно менять циклически .

использовать

Специальные матрицы

Транспонированная матрица используется в ряде определений линейной алгебры:

Симметричная матрица представляет собой квадратную матрицу , которая равна транспонированной: А. Т знак равно А. > = А>
Кососимметрична квадратная матрица, равная отрицательному ее транспонированной: А. Т знак равно - А. > = - A>
Эрмитова матрица представляет собой комплекс квадратной матрицы, транспонирование которой равен его конъюгат : А. Т знак равно А. ¯ > = >
Перекос эрмитова матрица представляет собой комплекс квадратной матрицы, транспонирование которой равен отрицательный его конъюгат: А. Т знак равно - А. ¯ > = - >
Ортогональная матрица является квадратной матрицей, транспонирование которой равнозначно обращению: А. Т знак равно А. - 1 > = А ^ >
(Реальная) нормальная матрица - это вещественная квадратная матрица, которая коммутирует со своим транспонированием : А. Т А. знак равно А. А. Т > A = AA ^ >>
Для любой вещественной матрицы две матрицы Грама и всегда симметричны и положительно полуопределены . А. Т А. > A> А. А. Т <\ Displaystyle AA ^ >>
Диадическое произведение двух векторов и дает матрицу . Икс у Икс у Т <\ displaystyle xy ^ >>

Билинейные формы

с регулярной матрицей тогда и только тогда, когда и представляют одну и ту же билинейную форму относительно, возможно, различных базисов. С. ∈ K п × п > А. Б. б : V × V → K

Двойные сопоставления

Матрица отображения двойственного отображения по отношению к дуальным базам, следовательно, в точности является транспонированной матрицей отображения прямого отображения по отношению к прямым базам. В физике это понятие используется для ковариантных и контравариантных векторных величин.

Присоединенные отображения

В реальных матрицах , таким образом , что приводит к заданной матрице присоединенной матрице просто транспонированная матрица, то есть . В функциональном анализе это понятие обобщается на сопряженные операторы между бесконечномерными гильбертовыми пространствами. А. * знак равно А. Т = A ^ >>

Перестановки

Транспонированная матрица также определяет специальные перестановки . Если числа от до записываются строка за строкой в матрицу, а затем считываются снова столбец за столбцом (что в точности соответствует транспонированию матрицы), результатом является перестановка этих чисел, которая ( м × п ) 1 м ⋅ п π

π ( п ( я - 1 ) + j ) знак равно я + м ( j - 1 )

для и можно указать. Число недостатков и , таким образом , также знак из может быть явно проходит через я знак равно 1 , . , м j знак равно 1 , . , п π

определять. В теории чисел , например, в лемме Золотарева , эти перестановки используются для доказательства квадратичного закона взаимности .

Обобщения

В более общем смысле можно также рассматривать матрицы с элементами из кольца (возможно, с одним ), в результате чего сохраняется большая часть свойств транспонированных матриц. Однако в произвольных кольцах ранг столбца матрицы не обязательно должен совпадать с рангом ее строки. Формула произведения и детерминантное представление действительны только в коммутативных кольцах .

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2. m; j=1,2. n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j- номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

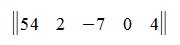
Матрица столбец

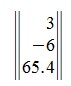
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

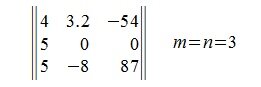
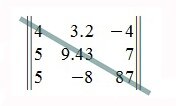
Главная диагональ матрицы

Элементы расположенные на местах a₁₁, a₂₂ . a_nn образуют главную диагональ матрицы. Например:

В случае m×n -матриц элементы a_ii ( i=1,2. min(m,n)) также образуют главную диагональ. Например:

Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .

Побочная диагональ матрицы

Элементы расположенные на местах a_1n, a_2n-1 . a_n1 образуют побочную диагональ матрицы. Например:

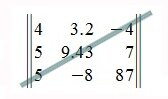
Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

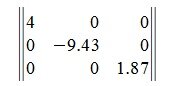
Единичная матрица

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n , где n - порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

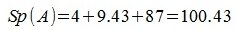
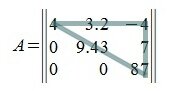
Верхняя треугольная матрица

Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. a_ij=0, при всех i>j . Например:

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i<j. Например:

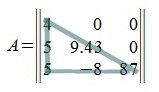
Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(A T ).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x- вектор длины n - образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).

Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

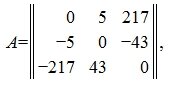
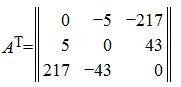
Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

Для обозначения разности двух матриц используется запись:

Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

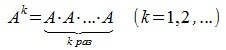
где E-единичная матрица.

Из сочетательного свойства умножения следует:

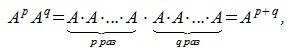
где p,q- произвольные целые неотрицательные числа.

Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

Читайте также: