Математическое и компьютерное моделирование что это
По окончании срока обучения студенты получают квалификацию “бакалавр математического и компьютерного моделирования” и могут занимать следующие должности:
- специалиста, ведущего специалиста, ведущего инженера, инженера-программиста в организационно-управленческих организациях;
- младшего научного сотрудника в научно-исследовательских институтах;
- преподавателя математики, информатики, физики в средне-профессиональных и технических образовательных организациях;
- в научно-исследовательских организациях в качестве научного сотрудника, ведущего инженера или математика-программиста как разработчик математических моделей физико-химических и технологических процессов;
- в проектных организациях как разработчик математических и компьютерных моделей, математик-программист;
- в организационно-технологических организациях как инженер-математик, математик-программист, разработчик математических и компьютерных моделей или специалист по информатике;
- в производственно-управленческих организациях как математик-программист и специалист по информатике;
- в средних и высших образовательных организациях как преподаватель или ассистент дисциплин математического и механического циклов и информатики;
- в средних школах как учитель математики, информатики и физики;
- системного программиста, системного администратора компьютерных сетей.
Квалификационная характеристика бакалавра специальности 050705 – Математическое и компьютерное моделирование
Сфера профессиональной деятельности
Сферами профессиональной деятельности выпускников являются:
- математические и алгоритмические модели научно-технических информационных процессов;
- математическое моделирование научно-технологических процессов;
- вычислительная математика, вычислительные технологии;
- базы данных и базы знаний;
- программы, программные системы и комплексы, технологии их проектирования;
- администрирование сетей.
Объекты профессиональной деятельности
Объектами профессиональной деятельности выпускников являются:
- научно-исследовательские организации;
- телекоммуникационные организации;
- образовательные организации;
- промышленное производство.
Предметы профессиональной деятельности
Предметами профессиональной деятельности выпускников являются:
- теоретические знания разработки математических моделей для естественных процессов;
- практические эксперименты вычислительного процесса;
- знания компьютерной и вычислительной технологии;
- знание сетевых технологий.
Виды профессиональной деятельности
Бакалавры по специальности 050705 – Математическое и компьютерное моделирование могут выполнять следующие виды профессиональной деятельности:
- научно-исследовательская;
- проектная;
- производственно-технологическая;
- организационно-управленческая;
- образовательная.
Функции профессиональной деятельности
Бакалавры по специальности 050705 – Математическое и компьютерное моделирование могут выполнять следующие функции профессиональной деятельности:
- обеспечение научными знаниями в области компьютерного и математического моделирования;
- поддержка компьютерных сетей в области администрирования и управления;
- обучение в образовательной системе.
Типовые задачи профессиональной деятельности
Типовыми задачами профессиональной деятельности выпускников являются:
- разработка математических моделей для природных явлений;
- разработка математических моделей для физических процессов;
- разработка математических моделей для химико-технологических процессов;- программирование и администрирование сетей.
Направления профессиональной деятельности
Направлениями профессиональной деятельности специалистов по специальности 050705 – Математическое и компьютерное моделирование являются: математическое и компьютерное моделирование естественно-физических, химико-технологических и других процессов; системное администрирование операционных систем; программирование производственных и научных задач;
разработка и управление базы данных для хозяйственных, экономических и финансовых задач; компьютерная графика и анимация для архитектурных и дизайнерских задач; трехмерное моделирование и визуализация объектов и персонажей; и другие.
Содержание профессиональной деятельности
Содержанием профессиональной деятельности выпускников являются:
- создание математических моделей для физических, природных, химических, медицинских, биологических, экономических процесов;
- применение математических методов для численных расчетов;
- проектирование, управление и администрирование компьютерных сетей в административных центрах;
- разработка, создание и управление базы данных;
- программирование на высоко уровневых объектно-ориентированных языках;
- создание сложно анимационных эффектов.
Требования к ключевым компетенциям бакалавра по специальности 050705 – Математическое и компьютерное моделирование
Бакалавр математического и компьютерного моделирования должен:
иметь представление: о реально изучаемом объекте исследования, о структуре компьютерных сетей, взаимодействии объектов при создании базы данных;
знать: теоретические и практические основы математического моделирования физических, природных, медицинских, химических, биологических процессов, языки программирования высокого уровня, языки визуального программирования, языки моделирования, вычислительную технику, системное администрирование, компьютерные сети, операционные системы, прикладные программы пользовательского назначения, специализированные программы;
уметь: анализировать изучаемый объект, проектировать математическую модель, использовать математический аппарат для решения задачи, оптимально использовать вычислительную технику, разрабатывать базы данных, программировать;
иметь навыки: создания математических моделей, решения математических задач, разработки и реализации базы данных, программирования;
быть компетентным: в области математического и компьютерного моделирования, в области вычислительной математики и информатики, в преподавательской деятельности.
Содержание образовательных программ по специальности 050705 – Математическое и компьютерное моделирование
Общеобразовательные дисциплины
Обязательный компонент
История Казахстана
Философия
Иностранный язык
Казахский (русский) язык
Информатика
Экология
Физическая культура
Компонент по выбору
Базовые дисциплины
Обязательный компонент
Математический анализ – I
Математический анализ – II
Математический анализ – III
Аналитическая геометрия
Алгебра
Программирование
Дифференциальные уравнения
Введение в вычислительную математику
Теоретическая механика
Уравнения математической физики
Дискретная математика и математическая логика
Физика
Дифференциальная геометрия и топология
Механика сплошной среды
Теория вероятностей и математическая статистика
Компонент по выбору
Профильные дисциплины
Обязательный компонент
Системное администрирование операционных систем
Объектно-ориентированное программирование на языке С++
3D-моделирование
Введение в математическое моделирование
Основы математического и компьютерного моделирования химико-технологических процессов
Компьютерная графика (Open GL, DirectX)
Основы математического и компьютерного моделирования естественно-физических процессов
Компонент по выбору
Дополнительные виды обучения
Физическая культура
Практика
Учебная практика
Производственная практика
ПГК Промежуточныйгосударственный контроль
Итоговая государственная аттестация
1) Написание и защита дипломной работы (проекта).
2) Государственные экзамены по специальности (дисциплина).
Перечень ВУЗов ведущих набор студентов по специальности 050705 – Математическое и компьютерное моделирование
Математическая модель описывается (представляется) математическими структурами , математическим аппаратом (числа, буквы, геометрические образы, отношения, алгебраические структуры и т.д.).
У математических моделей есть и дидактические аспекты - развитие модельного и математического стиля мышления, позволяющего вникать в структуру и внутреннюю логику моделируемой системы.
Отметим основные операции (процедуры) математического моделирования .
1. Линеаризация . Пусть дана математическая модель М=М(X, Y, A) , где X - множество входов, Y - множество выходов, А - множество состояний системы. Схематически можно это изобразить так: X->A->Y . Если X , Y , A - линейные пространства ( множества ), а - линейные операторы (т.е. любые линейные комбинации ax+by аргументов и преобразуют в соответствующие линейные комбинации и , то система (модель) называется линейной . Все другие системы (модели) - нелинейные. Они труднее поддаются исследованию, хотя и более актуальны. Нелинейные модели менее изучены, поэтому их часто линеаризуют - сводят к линейным моделям каким-то образом, какой-то корректной линеаризующей процедурой.
Пример. Применим операцию идентификации параметра a в модели предыдущего примера. Для этого необходимо задать дополнительно значение y для некоторого t , например, y=6 при t=3 . Тогда из модели получаем: 6=9a/2 , a=12/9=4/3 . Идентифицированный параметр а определяет следующую модель y=2t 2 /3 . Методы идентификации моделей могут быть несоизмеримо сложнее, чем приведенный прием.
3. Оценка адекватности (точности) модели.
Пример. Оценим адекватность ( точность ) модели у=at 2 /2 , 0<=t<=4 , полученной в результате линеаризации выше. В качестве меры (критерия) адекватности рассмотрим привычную меру - абсолютное значение разности между точным (если оно известно) значением и значением, полученным по модели (почему берется по модулю?). Отклонение точной модели от линеаризованной будет в рамках этого критерия равно |at 2 /2-2at| , 0<=t<=4 . Если a>0 , то, как несложно оценить с помощью производной, эта погрешность будет экстремальна при t=2a . Например, если a=1 , то эта величина не превосходит 2. Это достаточно большое отклонение, и можно заключить, что наша линеаризованная модель в данном случае не является адекватной (как исходной системе, так и нелинеаризованной модели).
4. Оценка чувствительности модели (чувствительности к изменениям входных параметров).
Пример. Из предыдущего примера следует, что чувствительность модели у=at 2 /2 , 0<=t<=4 такова, что изменение входного параметра t на 1% приводит к изменению выходного параметра y на более, чем 2%, т.е. эта модель является чувствительной.
5. Вычислительный эксперимент по модели. Это эксперимент, осуществляемый с помощью модели на ЭВМ с целью определения, прогноза тех или иных состояний системы, реакции на те или иные входные сигналы. Прибором эксперимента здесь является компьютер (и модель!). Это процедура часто отождествляется с компьютерным моделированием.
Отметим основные причины, несколько тормозящие выход математического моделирования на новые информационные технологии :
- традиционное описание модели системами математических уравнений, соотношений; в то же время, большинство плохо структурированных и плохо формализуемых систем описываются с помощью экспертных данных, эвристических и имитационных процедур, интегрированных пакетов программ, графических образов и т.д.;
- существующие средства описания и представление моделей на ЭВМ не учитывают специфику моделирования, нет единого представления моделей, генерации новых моделей по банку моделей;
- недооценка возможностей компьютера, который может делать больше, чем простая реализация алгоритма, как правило, структурируемого и/или реализуемого хорошо, отсутствие доступа к опыту моделирования на ЭВМ.
В базовой пятерке: "система (исследуемая среда) - модель (описание среды) - алгоритм ( программа ) - компьютер (компьютерная технология) - пользователь (выработка решения)" при компьютерном моделировании главную роль играют уже алгоритм ( программа ), компьютер и технология, точнее, инструментальные системы для компьютера, компьютерные технологии.
Пример. При имитационном моделировании (при отсутствии строгого и формально записанного алгоритма) главную роль играют технология и средства моделирования; аналогичная ситуация наблюдается в когнитивной графике.
Моделирование является одним из способов познания мира.
Понятие моделирования достаточно сложное, оно включает в себя огромное разнообразие способов моделирования: от создания натуральных моделей (уменьшенных и или увеличенных копий реальных объектов) до вывода математических формул.
Для различных явлений и процессов бывают уместными разные способы моделирования с целью исследования и познания.
Объект, который получается в результате моделирования, называется моделью . Должно быть понятно, что это совсем не обязательно реальный объект. Это может быть математическая формула, графическое представление и т.п. Однако он вполне может заменить оригинал при его изучении и описании поведения.
Хотя модель и может быть точной копией оригинала, но чаще всего в моделях воссоздаются какие-нибудь важные для данного исследования элементы, а остальными пренебрегают. Это упрощает модель. Но с другой стороны, создать модель – точную копию оригинала – бывает абсолютно нереальной задачей. Например, если моделируется поведение объекта в условиях космоса. Можно сказать, что модель – это определенный способ описания реального мира.
- Создание модели.
- Изучение модели.
- Применение результатов исследования на практике и/или формулирование теоретических выводов.
Видов моделирования огромное количество. Вот некоторые примеры типов моделей:
Математические модели . Это знаковые модели, описывающие определенные числовые соотношения.
Графические модели. Визуальное представление объектов, которые настолько сложны, что их описание иными способами не дает человеку ясного понимания. Здесь наглядность модели выходит на первый план.
Имитационные модели. Позволяют наблюдать изменение поведения элементов системы-модели, проводить эксперименты, изменяя некоторые параметры модели.
Над созданием модели могут работать специалисты из разных областей, т.к. в моделировании достаточно велика роль межпредметных связей.
Совершенствование вычислительной техники и широкое распространение персональных компьютеров открыло перед моделированием огромные перспективы для исследования процессов и явлений окружающего мира, включая сюда и человеческое общество.
Компьютерное моделирование – это в определенной степени, то же самое, описанное выше моделирование, но реализуемое с помощью компьютерной техники.
Для компьютерного моделирования важно наличие определенного программного обеспечения.
При этом программное обеспечение, средствами которого может осуществляться компьютерное моделирование, может быть как достаточно универсальным (например, обычные текстовые и графические процессоры), так и весьма специализированными, предназначенными лишь для определенного вида моделирования.
Очень часто компьютеры используются для математического моделирования. Здесь их роль неоценима в выполнении численных операций, в то время как анализ задачи обычно ложится на плечи человека.
Обычно в компьютерном моделировании различные виды моделирования дополняют друг друга. Так, если математическая формула очень сложна, что не дает явного представления об описываемых ею процессах, то на помощь приходят графические и имитационные модели. Компьютерная визуализация может быть намного дешевле реального создания натуральных моделей.
С появлением мощных компьютеров распространилось графическое моделирование на основе инженерных систем для создания чертежей, схем, графиков.
Если система сложна, а требуется проследить за каждым ее элементом, то на помощь могут придти компьютерные имитационные модели. На компьютере можно воспроизвести последовательность временных событий, а потом обработать большой объем информации.
Однако следует четко понимать, что компьютер является хорошим инструментом для создания и исследования моделей, но он их не придумывает. Абстрактный анализ окружающего мира с целью воссоздания его в модели выполняет человек.
Одной из важных проблем в области разработки и создания современных сложных технических систем является исследование динамики их функционирования на различных этапах проектирования, испытания и эксплуатации. Сложными системами называются системы, состоящие из большого числа взаимосвязанных и взаимодействующих между собой элементов. При исследовании сложных систем возникают задачи исследования как отдельных видов оборудования и аппаратуры, входящих в систему, так и системы в целом.
К разряду сложных систем относятся крупные технические, технологические, энергетические и производственные комплексы.
При проектировании сложных систем ставится задача разработки систем, удовлетворяющих заданным техническим характеристикам. Поставленная задача может быть решена одним из следующих методов:
- методом синтеза оптимальной структуры системы с заданными характеристиками;
- методом анализа различных вариантов структуры системы для обеспечения требуемых технических характеристик.
Оптимальный синтез систем в большинстве случаев практически невозможен в силу сложности поставленной задачи и несовершенства современных методов синтеза сложных систем. Методы анализа сложных систем, включающие в себя элементы синтеза, в настоящее время достаточно развиты и получили широкое распространение.
Любая синтезированная или определенная каким-либо другим образом структура сложной системы для оценки ее показателей должна быть подвергнута испытаниям. Проведение испытаний системы является задачей анализа ее характеристик. Таким образом, конечным этапом проектирования сложной системы, осуществленного как методом синтеза структуры, так и методом анализа вариантов структур, является анализ показателей эффективности проектируемой системы.
Среди известных методов анализа показателей эффективности систем и исследования динамики их функционирования следует отметить:
- аналитический метод;
- метод натуральных испытаний;
- метод полунатурального моделирования;
- моделирование процесса функционирования системы на ЭВМ.
Строгое аналитическое исследование процесса функционирования сложных систем практически невозможно. Определение аналитической модели сложной системы затрудняется множеством условий, определяемых особенностями работы системы, взаимодействием ее составляющих частей, влиянием внешней среды и т.п.
Натуральные испытания сложных систем связаны с большими затратами времени и средств. Проведение испытаний предполагает наличие готового образца системы или ее физической модели, что исключает или затрудняет использование этого метода на этапе проектирования системы.
Широкое применение для исследования характеристик сложных систем находит метод полунатурального моделирования. При этом используется часть реальных устройств системы. Включенная в такую полунатуральную модель ЭВМ имитирует работы остальных устройств системы, отображенных математическими моделями. Однако в большинстве случаев этот метод также связан со значительными затратами и трудностями, в частности, аппаратной стыковкой натуральных частей с ЭВМ.
Исследование функционирования сложных систем с помощью моделирования их работы на ЭВМ помогает сократить время и средства на разработку.
Затраты рабочего времени и материальных средств на реализацию метода имитационного моделирования оказываются незначительными по сравнению с затратами, связанными с натурным экспериментом. Результаты моделирования по своей ценности для практического решения задач часто близки к результатам натурного эксперимента.
Метод имитационного моделирования основан на использовании алгоритмических (имитационных) моделей, реализуемых на ЭВМ, для исследования процесса функционирования сложных систем. Для реализации метода необходимо разработать специальный моделирующий алгоритм. В соответствии с этим алгоритмом в ЭВМ вырабатывается информация, описывающая элементарные процессы исследуемой системы с учетом взаимосвязей и взаимных влияний. При этом моделирующий алгоритм сроится в соответствии с логической структурой системы с сохранением последовательности протекаемых в ней процессов и отображением основных состояний системы.
Основными этапами метода имитационного моделирования являются:
- моделирование входных и внешних воздействий;
- воспроизведение работы моделируемой системы (моделирующий алгоритм);
- интерпретация и обработка результатов моделирования.
Перечисленные этапы метода многократно повторяются для различных наборов входных и внешних воздействий, образуя внутренний цикл моделирования. Во внешнем цикле организуется просмотр заданных вариантов моделируемой системы. Процедура выбора оптимального варианта управляет просмотром вариантов, внося соответствующие коррективы в имитационную модель и в модели входных и внешних воздействий.
Процедура построения модели системы, контроля точности и корректировки модели по результатам машинного эксперимента задает и затем изменяет блок и внутреннего цикла в зависимости от фактических результатов моделирования. Таким образом, возникает внешний цикл, отражающий деятельность исследователя по формированию, контролю и корректировке модели.
Метод имитационного моделирования позволяет решать задачи исключительной сложности. Исследуемая система может одновременно содержать элементы непрерывного и дискретного действия, быть подверженной влиянию многочисленных случайных факторов сложной природы, описываться весьма громоздкими соотношениями и т.п. Метод не требует создания специальной аппаратуры для каждой новой задачи и позволяет легко изменять значения параметров исследуемых систем и начальных условий. Эффективность метода имитационного моделирования тем более высока, чем на более ранних этапах проектирования системы он начинает использоваться.
Следует, однако, помнить, что метод имитационного моделирования является численным методом. Его можно считать распространением метода Монте-Карло на случай сложных систем. Как любой численный метод, он обладает существенным недостатком – его решение всегда носит частный характер. Решение соответствует фиксированным значениям параметров системы и начальных условий. Для анализа системы приходится многократно моделировать процесс ее функционирования, варьируя исходные данные модели. Таким образом, для реализации имитационных моделей сложной модели необходимо наличие ЭВМ высокой производительности.
Для моделирования системы на ЭВМ необходимо записывать моделирующий алгоритм на одном из входных языков ЭВМ. В качестве входных языков для решения задач моделирования могут быть с успехом использованы универсальные алгоритмические языки высокого уровня, Си, Паскаль и др.
Анализ развития наиболее сложных технических систем позволяет сделать вывод о все более глубоком проникновении ЭВМ в их структуру. Вычислительные машины становятся неотъемлемой, а зачастую и основной частью таких систем. Прежде всего это относится к сложным радиоэлектронным системам. Среди них различные автоматические системы, в том числе системы автоматической коммутации (электронные АТС), системы радиосвязи, радиотелеметрические системы, системы радиолокации и радионавигации, различные системы управления.
При построении таких систем в значительной степени используются принципы и структуры организации вычислительных машин и вычислительных систем (ВС). Характерной особенностью является наличие в системах нескольких процессоров, объединенных различными способами в специализированную ВС. При этом осуществляется переход от «жесткой» логики функционирования технических систем к универсальной «программной» логике. В силу этого все более значительную роль в таких системах, наряду с аппаратными средствами, играет специализированное системное и прикладное программное обеспечение.
На этапах разработки, проектирования, отладки и испытания сложных систем с высоким удельным весом аппаратно-программных средств вычислительной техники ставится задача анализа и синтеза вариантов организации структуры аппаратных средств, а также разработки и отладки специализированного ПО большого объема. Эта задача может быть решена с помощью аппаратно-программного моделирования с использованием универсальных моделирующих комплексов, построенных на базе однородных ВС с программируемой структурой.
Аппаратно-программное моделирование можно считать частным случаем полунатурного моделирования. На первом этапе разрабатывается концептуальная модель заданного класса систем на основе анализа типовых процессов, структур и аппаратных блоков. Концептуальная модель реализуется на аппаратно-программных средствах моделирующего комплекса. При этом моделирующий комплекс может настраиваться на соответствующую структуру системы программным путем за счет возможности программирования структуры используемой микропроцессорной ВС. Часть аппаратных и программных средств микропроцессорной ВС моделирующего комплекса непосредственно отражает аппаратно-программные средства, входящие в исследуемую систему (аппаратное моделирование), другая часть реализует имитационную модель функциональных средств исследуемой системы, внешней обстановки, влияния помех и т.п. (программное моделирование).
Разработка аппаратно-программных моделирующих комплексов является сложной технической задачей. Несмотря на это, применение таких комплексов находит все большее распространение. При достаточной производительности вычислительных средств комплекса процесс исследования системы может вестись в реальном масштабе времени. В составе комплекса могут использоваться как универсальные микроЭВМ общего назначение, так и вычислительные средства, непосредственно входящие в исследуемую систему. Подобные моделирующие комплексы являются универсальными стендами для разработки и отладки аппаратно-программных средств, проектируемых систем заданного класса. Они могут использоваться в качестве тренажеров по обучению обслуживающего персонала.
Для того чтобы понять суть математического моделирования, рассмотрим основные определения, особенности процесса.
Суть термина
Моделирование представляет собой процесс создания и применения модели. Ею считают любой абстрактный или материальный предмет, заменяющий в процессе изучения реальный объект моделирования. Важным моментом является сохранение свойств, необходимых для полноценного анализа предмета.
Компьютерное моделирование представляет собой вариант познания, базирующийся на математической модели. Она подразумевает систему неравенств, уравнений, логических знаковых выражений, которые в полной мере отображают все характеристики явления или объекта.
Математическое моделирование предполагает конкретные расчеты, применение вычислительной техники. Для того чтобы объяснить процесс, нужны дополнительные исследования. С этой задачей успешно справляется компьютерное моделирование.
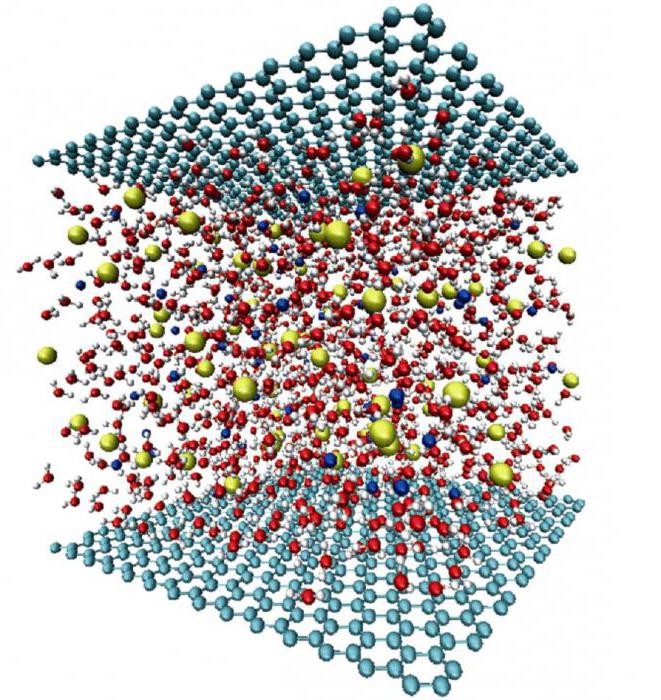
Специфичность компьютерного моделирования
Этот способ изучения сложных систем считают эффективным и результативным. Удобнее и проще анализировать именно компьютерные модели, поскольку можно осуществлять разнообразные вычислительные действия. Это особенно актуально в тех случаях, когда по физическим либо материальным причинам реальные эксперименты не позволяют получать желаемого результата. Логичность таких моделей дает возможность определять главные факторы, которые определяют параметры изучаемого оригинала.
Такое применение математического моделирования позволяет выявлять поведение объекта в различных условиях, выявлять влияние разных факторов на его поведение.
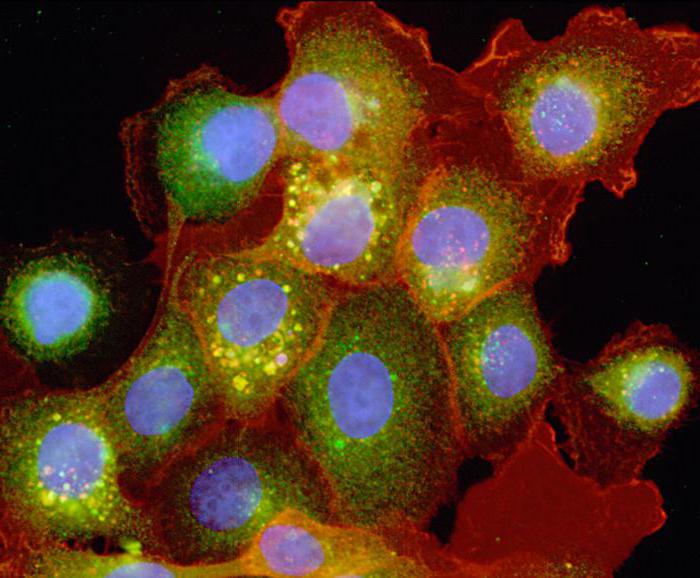
Основы компьютерного моделирования
На чем базируется такое моделирование? Что такое научные исследования на основе ИКТ? Начнем с того, что любое компьютерное моделирование основывается на определенных принципах:
- математическое моделирование для описания изучаемого процесса;
- применение инновационных математических моделей для детального рассмотрения изучаемых процессов.
Разновидности моделирования
В настоящее время выделяют разные методы математического моделирования: имитационное и аналитическое.
Аналитический вариант связан с изучением абстрактных моделей реального предмета в виде дифференциальных, алгебраических уравнений, которые предусматривают проведение четкой вычислительной техники, способной дать точное решение.
Имитационное моделирование предполагает исследование математической модели в виде определенного алгоритма, который воспроизводит функционирование анализируемой системы с помощью последовательного выполнения системы несложных вычислений и операций.

Особенности построения компьютерной модели
Подробнее рассмотрим, как происходит такое моделирование. Что такое этапы компьютерного исследования? Начнем с того, что процесс основывается на уходе от четкого объекта или анализируемого явления.
Такое моделирование состоит из двух основных этапов: создание качественной и количественной модели. Компьютерное изучение состоит в проведении системы вычислительных действий на персональном компьютере, направленных на анализ, систематизацию, сравнение результатов исследования с реальным поведением анализируемого объекта. В случае необходимости проводится дополнительное уточнение модели.

Этапы моделирования
Как осуществляется моделирование? Что такое этапы компьютерного исследования? Итак, выделяют следующий алгоритм действий, касающийся построения компьютерной модели:
1 этап. Постановка цели и задач работы, выявление объекта моделирования. Предполагается сбор данных, постановка вопроса, выявление целей и форм исследования, описание полученных результатов.
2 этап. Анализ и изучение системы. Осуществляется описание объекта, создание информационной модели, подбор программных и технических средств, подбираются примеры математического моделирования.
3 этап. Переход к математической модели, проработка метода проектирования, подбор алгоритма действий.
4 этап. Подбор языка программирования либо среды для моделирования, обсуждение вариантов анализа, записи алгоритма на определенном языке программирования.
5 этап. Он состоит в проведении комплекса вычислительных экспериментов, отладке расчетов, обработке полученных результатов. В случае необходимости, на данном этапе осуществляется корректировка моделирования.
6 этап. Интерпретация результатов.
Как анализируется проведенное моделирование? Что такое программные продукты для исследования? В первую очередь подразумевается использование текстовых, графических редакторов, электронных таблиц, математических пакетов, позволяющих получать максимальный результат от проведенных исследований.
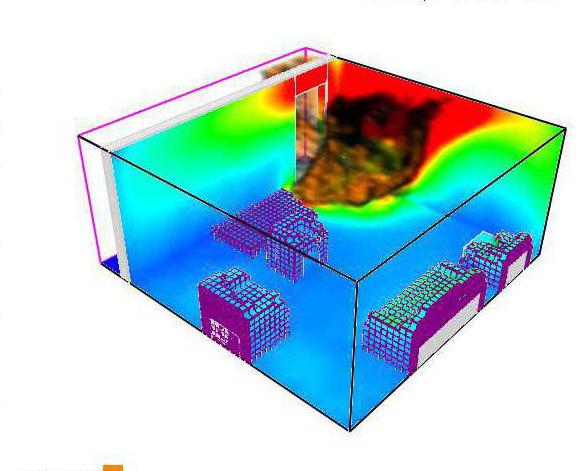
Проведение вычислительного эксперимента
Все методы математического моделирования базируются на экспериментах. Под ними принято понимать опыты, проводимые с моделью или объектом. Состоят они в осуществлении определенных действий, позволяющих определять поведение экспериментального образца в ответ на предлагаемые действия.
Вычислительный эксперимент невозможно представить без проведения расчетов, которые связаны с применением формализованной модели.
Основы математического моделирования предполагают проведение исследований с реальным объектом, но вычислительные действия проводят с его точной копией (моделью). При выборе конкретного набора исходных показателей модели, после завершения вычислительных действий, можно получать оптимальные условия для полноценного функционирования реального объекта.
К примеру, имея математическое уравнение, которое описывает протекание анализируемого процесса, при изменении коэффициентов, начальных и промежуточных условий, можно предположить поведение объекта. Кроме того, можно создать достоверный прогноз поведения этого объекта или природного явления в определенных условиях. В случае нового набора исходных данных важно проводить новые вычислительные эксперименты.

Сравнение полученных данных
Чтобы осуществить адекватную проверку реального объекта либо созданной математической модели, а также оценить результаты исследований на вычислительной технике с результатами эксперимента, проведенного на натурном опытном образце, осуществляется сравнение результатов исследований.
От того, каково расхождение между сведениями, полученными в ходе исследований, зависит решение о построении готового образца либо о корректировке математической модели.
Подобный эксперимент дает возможность заменять натуральные дорогостоящие исследования расчетами на вычислительной технике, за минимальные временные сроки анализировать возможности применения объекта, выявлять условия его реальной эксплуатации.
Моделирование в средах
Например, в среде программирования используется три этапа математического моделирования. На этапе создания алгоритма и информационной модели определяют величины, которые будут являться входными параметрами, результатами исследования, выявляют их тип.
В случае необходимости составляют специальные математические алгоритмы в виде блок-схем, записываемые на определенном языке программирования.
Далее осуществляется сам вычислительный эксперимент, для чего программу загружают в оперативную память вычислительного устройства, затем запускают процесс расчетов.
Компьютерный эксперимент предполагает анализ полученных при расчетах результатов, их корректировку. Среди важных этапов подобного исследования отметим проведение тестирования алгоритма, анализ работоспособности программы.
Ее отладка подразумевает поиск и устранение ошибок, которые приводят к нежелательному результату, появлению погрешностей в вычислениях.
Тестирование предполагает проверку правильности функционирования программы, а также оценку достоверности отдельных ее компонентов. Процесс состоит в проверке работоспособности программы, ее пригодности для изучения определенного явления или объекта.

Электронные таблицы
Моделирование с помощью электронных таблиц позволяет охватывать большой объем задач в различных предметных направлениях. Их считают универсальным инструментом, который позволяет решать трудоемкую задачу по расчету количественных параметров объекта.
В случае такого варианта моделирования наблюдается некоторая трансформация алгоритма решения задачи, нет необходимости разрабатывать вычислительный интерфейс. При этом присутствует этап отладки, который включает в себя удаление ошибок данных, поиск связи между ячейками, выявление вычислительных формул.
По мере работы появляются и дополнительные задачи, например вывод результатов на бумажные носители, рациональное представление информации на компьютерном мониторе.
Последовательность действий
Осуществляется моделирование в электронных таблицах по определенному алгоритму. Сначала определяются цели исследования, выявляются основные параметры и связи, на основе полученной информации составляется конкретная математическая модель.
Для качественного рассмотрения модели используют начальные, промежуточные, а также конечные характеристики, дополняют их чертежами, схемами. С помощью графиков и диаграмм получают наглядное представление о результатах работы.
Моделирование в среде СУБД
Оно позволяет решать следующие задачи:
- хранить информацию, проводить ее своевременное редактирование;
- упорядочивать имеющиеся данные по конкретным признакам;
- создавать разные критерии для подбора данных;
- представлять имеющиеся сведения в удобном виде.
По мере разработки модели на базе исходных данных создаются оптимальные условия для описания характеристик объекта с помощью специальных таблиц.
При этом осуществляется сортировка информации, поиск и фильтрация данных, создание алгоритмов для проведения вычислений. С помощью компьютерной информационной панели можно создавать разные экранные формы, а также варианты для получения печатных бумажных отчетов о ходе эксперимента.
При несовпадении полученных результатов с планируемыми вариантами меняют параметры, проводят дополнительные исследования.
Применение компьютерной модели
Вычислительный эксперимент и компьютерное моделирование являются новыми научными методами исследования. Они позволяют модернизировать вычислительный аппарат, применяемый для построения математической модели, конкретизировать, уточнять, усложнять эксперименты.
Среди самых перспективных для практического использования, проведения полноценного вычислительного эксперимента выделяют проектирование реакторов для мощных атомных станций. Кроме того, сюда относят создание магнитогидродинамических преобразователей электрической энергии, а также сбалансированного перспективного плана для страны, региона, отрасли.
Именно с помощью компьютерного и математического моделирования можно проводить проектирование приборов, необходимых для изучения термоядерных реакций, химических процессов.
Компьютерное моделирование и вычислительные эксперименты дают возможность сводить далеко «не математические» объекты к составлению и решению математической задачи.
Это открывает большие возможности для применения математического аппарата в системе с современной вычислительной техникой для решения вопросов, касающихся освоения космического пространства, «покорения» атомных процессов.
Именно моделирование стало одним из важнейших вариантов познания различных окружающих процессов и природных явлений. Это познание является сложным и трудоемким процессом, подразумевает применение системы различных видов моделирования, начиная с разработки уменьшенных моделей реальных объектов, завершая подбором специальных алгоритмов для проведения сложных математических вычислений.
В зависимости от того, какие процессы или явления будут анализироваться, подбираются определенные алгоритмы действий, математические формулы для вычислений. Компьютерное моделирование позволяет с минимальными затратами получать желаемый результат, важную информацию о свойствах и параметрах объекта либо явления.
Любое явление или объект обладает огромным количеством свойств, характеристик или параметров, охватить которые бывает очень сложно, поэтому приходится проводить упрощение такого объекта, отбрасывая несущественные детали. Иными словами, строить модель.
Под моделью мы будем понимать любой материальный или идеальный объект, обладающий некоторыми свойствами, совпадающими со свойствами реального объекта.



При этом исследователь будет выбирать такие свойства, которые являются существенными для изучаемого объекта. Например, при проектировке здания архитектору важен внешний вид объекта, для инженера — прочность и материалы, для инженера-геолога – нагрузка на грунт. Поэтому модель одного и того же здания будет различна.
Давайте рассмотрим еще один класс моделей — это математические модели. Например, все геометрические объекты (круг, треугольник, прямая) являются моделями. В окружающем нас мире не существует таких объектов.
Например, стол. Можем ли мы сказать, что он идеально прямоугольный? Нет, конечно, так как каждый край стола не может быть идеальной прямой линией. Однако, во многих случаях можно считать, что это так.
Подобные рассуждения справедливы и для всех других математических объектов — вектор, числа, функций, производных, интегралов.
Будем считать, что математическое моделирование — это описание реальной ситуации с помощью математических терминов, математических операций и математической символики.

Основоположником математического моделирования в России был академик Российской академии наук Александр Андреевич Самарский, который первый предложил использовать математические модели, реализуемые с помощью компьютера и дальнейшее их исследование. Важнейшим преимуществом использования таких моделей заключается в невысоких финансовых затратах и относительной простоте. При этом практика является и остается критерием истинности и завершающим звеном в исследовании.

Моделирование требует четкого плана действий. На первом этапе формируется задача, которую необходимо решить с помощью модели, далее разрабатывается некий математический эквивалент исследуемого объекта, после чего происходит тестирование такой модели и сравнение с практическими знаниями. Если модель на тестовом этапе не противоречит практике, то проводится эксперимент с моделью, после чего анализируются результаты и делаются выводы. Давайте рассмотрим все этапы моделирования на примере колеса, вращающегося внутри более большого:
ЭТАП 1. Постановка задачи
В колесе радиуса R катится колесо радиуса r. Какую траекторию описывает точка, расположенная на ободе колеса r?
ЭТАП 2. Математическая модель
Траектория движения этой точки находится по формулам:

где φ изменяется от 0 до 2π (угол смещения колеса r).
Вывод уравнения движения смотри по ссылке .
ЭТАП 3. Алгоритм решения
Для получения траектории движения колеса, нам необходимо изменять значение φ от 0 до 30. Вычислять координаты и представлять их на графике. Попробуем это сделать с помощью программы Excel.
ЭТАП 4. Разработка программы. Тестирование
Создадим таблицу по образцу:

В столбец А занесем значения угла φ от 0 до 6.28 с шагом 0.01.


Запишем в ячейку а в ячейку
С помощью маркера заполнения распространим эти формулы до конца таблицы.

По значениям столбцов B и С построим точечный график:

ЭТАП 5. Вычислительный эксперимент
Изменяя значения в ячейках F3 и F4, получи различные картинки:
ЭТАП 6. Анализ результатов. Выводы
Вычислительный эксперимент показал, что вид фигуры зависит от отношения радиусов маленького и большого колеса. Такие фигуры носят названия — ГИПОЦИКЛЫ.
Читайте также:


