Коллизия в хешировании это
В хэш-таблице обработка новых индексов производится при помощи ключей. А элементы, связанные с этим ключом, сохраняются в индексе. Этот процесс называется хэшированием.
Пусть k — ключ, а h(x) — хэш-функция.
Тогда h(k) в результате даст индекс, в котором мы будем хранить элемент, связанный с k .
Коллизии
Когда хэш-функция генерирует один индекс для нескольких ключей, возникает конфликт (неизвестно, какое значение нужно сохранить в этом индексе). Это называется коллизией хэш-таблицы.
Есть несколько методов борьбы с коллизиями:
- Метод цепочек.
- Метод открытой адресации: линейное и квадратичное зондирование.
1. Метод цепочек
Суть этого метода проста: если хэш-функция выделяет один индекс сразу двум элементам, то храниться они будут в одном и том же индексе, но уже с помощью двусвязного списка.
Если j — ячейка для нескольких элементов, то она содержит указатель на первый элемент списка. Если же j пуста, то она содержит NIL .
Псевдокод операций
2. Открытая адресация
В отличие от метода цепочек, в открытой адресации несколько элементов в одной ячейке храниться не могут. Суть этого метода заключается в том, что каждая ячейка либо содержит единственный ключ, либо NIL .
Существует несколько видов открытой адресации:
a) Линейное зондирование
Линейное зондирование решает проблему коллизий с помощью проверки следующей ячейки.
h(k, i) = (h′(k) + i) mod m ,
Если коллизия происходит в h(k, 0) , тогда проверяется h(k, 1) . То есть, значение i увеличивается линейно.
Проблема линейного зондирования заключается в том, что заполняется кластер соседних ячеек. Это приводит к тому, что при вставке нового элемента в хэш-таблицу необходимо проводить полный обход кластера. В результате время выполнения операций с хэш-таблицами увеличивается.
b) Квадратичное зондирование
Работает оно так же, как и линейное — но есть отличие. Оно заключается в том, что расстояние между соседними ячейками больше (больше одного). Это возможно благодаря следующему отношению:
- c1 и c2 — положительные вспомогательные константы,
- i =
c) Двойное хэширование
Если коллизия возникает после применения хэш-функции h(k) , то для поиска следующей ячейки вычисляется другая хэш-функция.
h(k, i) = (h1(k) + ih2(k)) mod m
«Хорошие» хэш-функции
«Хорошие» хэш-функции не уберегут вас от коллизий, но, по крайней мере, сократят их количество.
Ниже мы рассмотрим различные методы определения «качества» хэш-функций.
1. Метод деления
Если k — ключ, а m — размер хэш-таблицы, то хэш-функция h() вычисляется следующим образом:
Например, если m = 10 и k = 112 , то h(k) = 112 mod 10 = 2 . То есть, значение m не должно быть степенью 2. Это связано с тем, что степени двойки в двоичном формате — 10, 100, 1000… При вычислении k mod m мы всегда будем получать p-биты низшего порядка.
2. Метод умножения
- kA mod 1 отделяет дробную часть kA ,
- ⌊ ⌋ округляет значение
- A — произвольная константа, значение которой должно находиться между 0 и 1. Оптимальный вариант ≈ (√5-1) / 2, его предложил Дональд Кнут.
3. Универсальное хеширование
В универсальном хешировании хеш-функция выбирается случайным образом и не зависит от ключей.
Разрешение коллизий (англ. collision resolution) в хеш-таблице, задача, решаемая несколькими способами: метод цепочек, открытая адресация и т.д. Очень важно сводить количество коллизий к минимуму, так как это увеличивает время работы с хеш-таблицами.
Содержание

Каждая ячейка [math]i[/math] массива [math]H[/math] содержит указатель на начало списка всех элементов, хеш-код которых равен [math]i[/math] , либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.
В зависимости от того нужна ли нам уникальность значений операции вставки у нас будет работать за разное время. Если не важна, то мы используем список, время вставки в который будет в худшем случае равна [math]O(1)[/math] . Иначе мы проверяем есть ли в списке данный элемент, а потом в случае его отсутствия мы его добавляем. В таком случае вставка элемента в худшем случае будет выполнена за [math]O(n)[/math]
Время работы поиска в наихудшем случае пропорционально длине списка, а если все [math]n[/math] ключей захешировались в одну и ту же ячейку (создав список длиной [math]n[/math] ) время поиска будет равно [math]\Theta(n)[/math] плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех [math]n[/math] элементов.
Удаления элемента может быть выполнено за [math]O(1)[/math] , как и вставка, при использовании двухсвязного списка.

Все элементы хранятся непосредственно в хеш-таблице, без использования связных списков. В отличие от хеширования с цепочками, при использовании этого метода может возникнуть ситуация, когда хеш-таблица окажется полностью заполненной, следовательно, будет невозможно добавлять в неё новые элементы. Так что при возникновении такой ситуации решением может быть динамическое увеличение размера хеш-таблицы, с одновременной её перестройкой.
Последовательный поиск
При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+1, i+2, i+3[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.

Линейный поиск
Выбираем шаг [math]q[/math] . При попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math]i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)[/math] и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск - частный случай линейного, где [math]q=1[/math] .
Квадратичный поиск
Шаг [math]q[/math] не фиксирован, а изменяется квадратично: [math]q = 1,4,9,16. [/math] . Соответственно при попытке добавить элемент в занятую ячейку [math]i[/math] начинаем последовательно просматривать ячейки [math] i+1, i+4, i+9[/math] и так далее, пока не найдём свободную ячейку.

Проверка осуществляется аналогично добавлению: мы проверяем ячейку [math]i[/math] и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.
При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.
Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.
Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется двойное хеширование и хеширование кукушки.
Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на [math]q[/math] позиций назад. При этом:
- если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
- в цепочке не должно оставаться "дырок", тогда любой элемент с данным хешем будет доступен из начала цепи
Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).
Хеш-таблицу считаем зацикленной
Асимптотически время работы [math]\mathrmВариант с зацикливанием мы не рассматриваем, поскольку если [math]q[/math] взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций
Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.
Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце [math]\mathrm[/math] (см. псевдокод) заметёт созданную дыру (скопированный элемент), и сам, по предположению, новых не создаст.
- Элементы, которые уже на своих местах, не должны быть сдвинуты.
Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на [math]q[/math] позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.
Двойное хеширование (англ. double hashing) — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.
При двойном хешировании используются две независимые хеш-функции [math] h_1(k) [/math] и [math] h_2(k) [/math] . Пусть [math] k [/math] — это наш ключ, [math] m [/math] — размер нашей таблицы, [math]n \bmod m [/math] — остаток от деления [math] n [/math] на [math] m [/math] , тогда сначала исследуется ячейка с адресом [math] h_1(k) [/math] , если она уже занята, то рассматривается [math] (h_1(k) + h_2(k)) \bmod m [/math] , затем [math] (h_1(k) + 2 \cdot h_2(k)) \bmod m [/math] и так далее. В общем случае идёт проверка последовательности ячеек [math] (h_1(k) + i \cdot h_2(k)) \bmod m [/math] где [math] i = (0, 1, \; . \;, m - 1) [/math]
Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за [math]O(1)[/math] , в худшем — за [math]O(m)[/math] , что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.
[math]\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))[/math]
[math] h_1 [/math] может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, [math] h_2 [/math] должна возвращать значения:
- не равные [math] 0 [/math]
- независимые от [math] h_1 [/math]
- взаимно простые с величиной хеш-таблицы
Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а [math] h_2 [/math] возвращает натуральные числа, меньшие [math] m [/math] . Второй — размер таблицы является степенью двойки, а [math] h_2 [/math] возвращает нечетные значения.
Например, если размер таблицы равен [math] m [/math] , то в качестве [math] h_2 [/math] можно использовать функцию вида [math] h_2(k) = k \bmod (m-1) + 1 [/math]
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:
[math] h(k,i) = (h_1(k) + i \cdot h_2(k)) \bmod 13 [/math]
[math] h_1(k) = k \bmod 13 [/math]
[math] h_2(k) = 1 + k \bmod 11 [/math]
Мы хотим вставить ключ 14. Изначально [math] i = 0 [/math] . Тогда [math] h(14,0) = (h_1(14) + 0\cdot h_2(14)) \bmod 13 = 1 [/math] . Но ячейка с индексом 1 занята, поэтому увеличиваем [math] i [/math] на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При [math] i = 2 [/math] получаем [math] h(14,2) = (h_1(14) + 2\cdot h_2(14)) \bmod 13 = 9 [/math] . Ячейка с номером 9 свободна, значит записываем туда наш ключ.
Таким образом, основная особенность двойного хеширования состоит в том, что при различных [math] k [/math] пара [math] (h_1(k),h_2(k)) [/math] дает различные последовательности ячеек для исследования.
Пусть у нас есть некоторый объект [math] item [/math] , в котором определено поле [math] key [/math] , от которого можно вычислить хеш-функции [math] h_1(key)[/math] и [math] h_2(key) [/math]
Так же у нас есть таблица [math] table [/math] величиной [math] m [/math] , состоящая из объектов типа [math] item [/math] .
Чтобы наша хеш-таблица поддерживала удаление, требуется добавить массив [math]deleted[/math] типов [math]bool[/math] , равный по величине массиву [math]table[/math] . Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.
В Java 8 для разрешения коллизий используется модифицированный метод цепочек. Суть его заключается в том, что когда количество элементов в корзине превышает определенное значение, данная корзина переходит от использования связного списка к использованию сбалансированного дерева. Но данный метод имеет смысл лишь тогда, когда на элементах хеш-таблицы задан линейный порядок. То есть при использовании данный типа [math]\mathbf[/math] или [math]\mathbf[/math] имеет смысл переходить к дереву поиска, а при использовании каких-нибудь ссылок на объекты не имеет, так как они не реализуют нужный интерфейс. Такой подход позволяет улучшить производительность с [math]O(n)[/math] до [math]O(\log(n))[/math] . Данный способ используется в таких коллекциях как HashMap, LinkedHashMap и ConcurrentHashMap.
Коллизией хеш-функции H называется два различных входных блока данных x и y таких, что H(x) = H(y).
Содержание
Коллизии криптографических хеш-функций
Мерой криптостойкости хеш-функции является вычислительная сложность нахождения коллизии. Так как криптографические хеш-функции используются для подтверждения неизменности исходной информации (например, для создания цифровой подписи), то найти коллизию для них должно быть сложно (не проще чем полным перебором).
Для криптографических хеш-функций различают два типа стойкости к нахождению коллизий:
Пожалуй, самой простой атакой на нахождение коллизий является атака «дней рождения». С помощью этой атаки отыскание коллизии для хеш-функции разрядности n бит потребует в среднем около 2 n / 2 операций. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для нее близка к 2 n / 2 .
Также ключевым свойством хеш-функций является их необратимость:
- Под необратимостью понимается вычислительная невозможность нахождения исходного блока данных X по известному значению хеш-функции от этого блока H(X) .
На этом свойстве основано большинство методов применения хеш-функций в криптографии. В качестве примера можно рассмотреть простую процедуру аутентификации пользователя: при регистрации в системе пользователь вводит свой пароль, к которому применяется хеш-функция и результат записывается в базу данных; далее при каждом вводе пароля, он хешируется и результат сравнивается с тем, который записан в БД. При таком подходе даже если злоумышленник получит доступ к базе данных, он не сможет восстановить исходные пароли пользователей (при условии того, что обеспечено свойство необратимости хеш-функции). Однако, если злоумышленник умеет находить коллизии для этой хеш-функции, ему не составит труда найти поддельный пароль, который будет иметь хеш одинаковый с паролем пользователя.
Большая часть современных хеш-функций имеют одинаковую структуру, основанную на разбиении входного текста на блоки и последующем итерационном процессе, в котором на каждой итерации используется некоторая функция G(x,y) , где x — очередной блок входного текста, а y — результат предыдущй операции. Однако такая схема несовершенна, так как, зная функцию G , мы можем проводить анализ данных в промежутках между итерациями, что облегчает поиск коллизий.
Разрешение коллизий в хеш-таблицах
Коллизии осложняют использование хеш-таблиц, так как нарушают однозначность соответствия между хеш-кодами и данными. Тем не менее, существуют специальные методики для преодоления возникающих сложностей:
Цель лекции: изучить построение функции хеширования и алгоритмов хеширования данных и научиться разрабатывать алгоритмы открытого и закрытого хеширования при решении задач на языке C++.
Процесс поиска данных в больших объемах информации сопряжен с временными затратами, которые обусловлены необходимостью просмотра и сравнения с ключом поиска значительного числа элементов. Сокращение поиска возможно осуществить путем локализации области просмотра. Например, отсортировать данные по ключу поиска, разбить на непересекающиеся блоки по некоторому групповому признаку или поставить в соответствие реальным данным некий код, который упростит процедуру поиска.
В настоящее время используется широко распространенный метод обеспечения быстрого доступа к информации, хранящейся во внешней памяти – хеширование .
Хеш-таблица – это структура данных , реализующая интерфейс ассоциативного массива, то есть она позволяет хранить пары вида " ключ - значение " и выполнять три операции : операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу. Хеш-таблица является массивом, формируемым в определенном порядке хеш-функцией .
Принято считать, что хорошей, с точки зрения практического применения, является такая хеш-функция , которая удовлетворяет следующим условиям:
- функция должна быть простой с вычислительной точки зрения;
- функция должна распределять ключи в хеш-таблице наиболее равномерно;
- функция не должна отображать какую-либо связь между значениями ключей в связь между значениями адресов;
- функция должна минимизировать число коллизий – то есть ситуаций, когда разным ключам соответствует одно значение хеш-функции (ключи в этом случае называются синонимами ).
При этом первое свойство хорошей хеш-функции зависит от характеристик компьютера, а второе – от значений данных.
Если бы все данные были случайными, то хеш-функции были бы очень простые (например, несколько битов ключа). Однако на практике случайные данные встречаются достаточно редко, и приходится создавать функцию, которая зависела бы от всего ключа. Если хеш-функция распределяет совокупность возможных ключей равномерно по множеству индексов, то хеширование эффективно разбивает множество ключей. Наихудший случай – когда все ключи хешируются в один индекс .
При возникновении коллизий необходимо найти новое место для хранения ключей, претендующих на одну и ту же ячейку хеш-таблицы. Причем, если коллизии допускаются, то их количество необходимо минимизировать. В некоторых специальных случаях удается избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую инъективную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий . Хеш-таблицы, использующие подобные хеш-функции , не нуждаются в механизме разрешения коллизий , и называются хеш-таблицами с прямой адресацией.
Хеш-таблицы должны соответствовать следующим свойствам.
- Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение является индексом в исходном массиве.
- Количество хранимых элементов массива, деленное на число возможных значений хеш-функции , называется коэффициентом заполнения хеш-таблицы ( load factor ) и является важным параметром, от которого зависит среднее время выполнения операций.
- Операции поиска, вставки и удаления должны выполняться в среднем за время O(1) . Однако при такой оценке не учитываются возможные аппаратные затраты на перестройку индекса хеш-таблицы, связанную с увеличением значения размера массива и добавлением в хеш-таблицу новой пары.
- Механизм разрешения коллизий является важной составляющей любой хеш-таблицы.
Хеширование полезно, когда широкий диапазон возможных значений должен быть сохранен в малом объеме памяти, и нужен способ быстрого, практически произвольного доступа. Хэш-таблицы часто применяются в базах данных, и, особенно, в языковых процессорах типа компиляторов и ассемблеров , где они повышают скорость обработки таблицы идентификаторов. В качестве использования хеширования в повседневной жизни можно привести примеры распределение книг в библиотеке по тематическим каталогам, упорядочивание в словарях по первым буквам слов, шифрование специальностей в вузах и т.д.
Методы разрешения коллизий
Коллизии осложняют использование хеш-таблиц, так как нарушают однозначность соответствия между хеш-кодами и данными. Тем не менее, существуют способы преодоления возникающих сложностей:
- метод цепочек (внешнее или открытое хеширование );
- метод открытой адресации (закрытое хеширование ).
Метод цепочек. Технология сцепления элементов состоит в том, что элементы множества , которым соответствует одно и то же хеш- значение , связываются в цепочку- список . В позиции номер i хранится указатель на голову списка тех элементов, у которых хеш- значение ключа равно i ; если таких элементов в множестве нет, в позиции i записан NULL . На рис. 38.1 демонстрируется реализация метода цепочек при разрешении коллизий . На ключ 002 претендуют два значения, которые организуются в линейный список .
Рис. 38.1. Разрешение коллизий при помощи цепочек
Каждая ячейка массива является указателем на связный список (цепочку) пар ключ - значение , соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.
Операции поиска или удаления данных требуют просмотра всех элементов соответствующей ему цепочки, чтобы найти в ней элемент с заданным ключом. Для добавления данных нужно добавить элемент в конец или начало соответствующего списка, и, в случае если коэффициент заполнения станет слишком велик, увеличить размер массива и перестроить таблицу.
При предположении, что каждый элемент может попасть в любую позицию таблицы с равной вероятностью и независимо от того, куда попал любой другой элемент, среднее время работы операции поиска элемента составляет O(1+k) , где k – коэффициент заполнения таблицы.
Метод открытой адресации. В отличие от хеширования с цепочками, при открытой адресации никаких списков нет, а все записи хранятся в самой хеш-таблице. Каждая ячейка таблицы содержит либо элемент динамического множества , либо NULL .
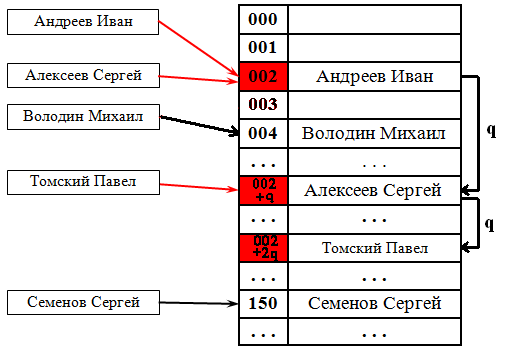
В этом случае, если ячейка с вычисленным индексом занята, то можно просто просматривать следующие записи таблицы по порядку до тех пор, пока не будет найден ключ K или пустая позиция в таблице. Для вычисления шага можно также применить формулу, которая и определит способ изменения шага. На рис. 38.2 разрешение коллизий осуществляется методом открытой адресации. Два значения претендуют на ключ 002, для одного из них находится первое свободное (еще незанятое) место в таблице.
Рис. 38.2. Разрешение коллизий при помощи открытой адресации
При любом методе разрешения коллизий необходимо ограничить длину поиска элемента. Если для поиска элемента необходимо более 3 – 4 сравнений, то эффективность использования такой хеш-таблицы пропадает и ее следует реструктуризировать (т.е. найти другую хеш-функцию), чтобы минимизировать количество сравнений для поиска элемента
Для успешной работы алгоритмов поиска, последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.
Удаление элементов в такой схеме несколько затруднено. Обычно поступают так: заводят логический флаг для каждой ячейки, помечающий, удален ли элемент в ней или нет. Тогда удаление элемента состоит в установке этого флага для соответствующей ячейки хеш-таблицы, но при этом необходимо модифицировать процедуру поиска существующего элемента так, чтобы она считала удаленные ячейки занятыми, а процедуру добавления – чтобы она их считала свободными и сбрасывала значение флага при добавлении.
Читайте также: