Какая логика управляет действиями компьютера
При объяснении нового материала используется презентация (Приложение 1).
- Логика – наука о формах и способах мышления
- Логика изучает внутреннюю структуру процесса мышления
- Алгебра логики – булева алгебра. Цель алгебры логики – описание поведения и структуры логических схем
Истинные высказывания правильно отражают свойства и отношения реальных вещей.
Ложные высказывания не соответствуют реальной действительности.
- Истинное высказывание правильно отражает свойства и отношение реальных вещей (2*2=4).
- Ложное высказывание не соответствует реальной действительности (2*2=5).
Логические операции задаются таблицами истинности.
Операция “ИЛИ” – “OR” – операция логического сложения:
Операция “И” – “AND” – операция логического умножения:
Операция “НЕ” – “NOT” – операция логического отрицания:
Импликация – логическое следование:
Составное высказывание, образованное с помощью операции логического следования (импликации) ложно тогда и только тогда, когда из истинной посылки (первого высказывания) следует ложный вывод (второе высказывание)
Составное высказывание, образованное с помощью логической операции эквивалентности, истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
- Логическое выражение – это выражение, которое включает в себя логические переменные, объединенные логическими операциями
- Таблица истинности определяет истинность или ложностьсоставного высказывания
Определить истинность или ложность логического высказывания:
A AND B OR C AND A
Инверсия, логическое умножение, логическое сложение.
| A | B | C | A and B | C and A | A and B or C and A |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Любое логическое выражение можно рассматривать как логическую функцию.
Логической функцией называют функцию F(x1, x2, …xn) – функция от логических переменных, которая может принимать значения либо логического “0”, либо логической “1”. Для каждой логической функции имеется таблица истинности логической функции.
Логическая функция может быть задана табличным способом или в виде соответствующих формул.
Каждая логическая функция 2-х аргументов имеет 4 возможных набора значений аргументов: 00, 01, 10, 11.
N = 2 4 = 16 различных логических функций.
Законы алгебры логики:
Закон исключения третьего
Закон двойного отрицания
Вопросы по теме: “Основы логики и логические основы компьютера”:
Практические задания по теме
Построить таблицу истинности по булеву выражению:
1. F(x1, x2, x3) = x3 \/ (2 & x1 & x3)
2. F(x1, x2, x3) = 1 & 2 \/ x2 \/ x1 & x3
3. F(x1, x2, x3) = 1 & x2 & x3 \/ 1 \/ x2 \/ x3
1. Информатика и ИКТ. Профильный уровень: учебник для 10 класса / Н.Д. Угринович.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
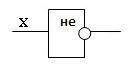
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
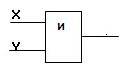
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
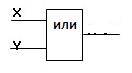
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Пример 1.
Составьте логическую схему для логического выражения: F=A \/ B /\ A.
1. Две переменные – А и В.
2. Две логические операции: 1-/\, 2-\/.
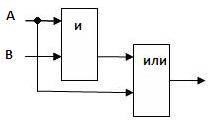
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
Основные логические элементы реализуют 3 основные логические операции:
- логическое умножение;
- логическое сложение;
- инверсию (отрицание).
Устройства компьютера, которые выполняют обработку и хранение информации, могут быть собраны из базовых логических элементов, у которых $2$ входа и $1$ выход. К логическим устройствам компьютера относятся группы переключателей, триггеры, сумматоры.
Связь между алгеброй логики и компьютерной техникой также лежит в двоичной системе счисления, которая используется в ЭВМ. Поэтому в устройствах ПК можно хранить и обрабатывать как числа, так и значения логических переменных.
Логический элемент компьютера – это часть электронной схемы, которая выполняет элементарную логическую функцию.
Переключательные схемы
В ЭВМ используются электрические схемы, которые состоят из большого количества переключателей. Переключатель, находясь в замкнутом состоянии ток пропускает, в разомкнутом – не пропускает. Работа таких схем удобно описывается при помощи алгебры логики. В зависимости от состояния переключателя можно регулировать получение или неполучение сигналов на выходах.
Вентили
Среди логических элементов компьютеров выделяют электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие (их называют вентили).
Эти схемы позволяют реализовать любую логическую функцию, которая описывает работу устройств ПК. Обычно вентили имеют $2–8$ входов и $1$ или $2$ выхода.
Для представления двух логических состояний ($1$ и $0$) в вентилях, входные и выходные сигналы имеют разные уровни напряжения. Например, $+3 \ B$ (вольт) для состояния $«1»$ и $0 \ B$ для состояния $«0»$.
У каждого логического элемента есть условное обозначение, выражающее его логическую функцию, но не указывающее на электронную схему, которая в нем реализована. Такой подход реализован для упрощения записи и понимания сложных логических схем.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимостьРабота логических элементов описывается таблицами истинности.

Триггер
Триггеры и сумматоры состоят из вентилей.
Триггер – важнейшая структурная единица оперативной памяти ПК и внутренних регистров процессора.
Триггер – логическая схема, которая способна хранить $1$ бит информации ($1$ или $0$). Строится на $2$-х элементах ИЛИ–НЕ или на $2$-х элементах И–НЕ.

Самый распространённый тип триггера – $RS$-триггер (Reset/Set), который имеет $2$ входа $S$ и $R$ и два выхода $Q$ и $\bar$. На каждый из входов $S$ и $R$ могут подаваться входные сигналы в виде кратковременных импульсов (рис.3): есть импульс – $1$, нет импульса – $0$.

Рисунок 3. Кратковременный импульс
Сумматор
Сумматоры широко применяются в арифметико-логических устройствах процессора и отвечают за суммирование двоичных разрядов.
Сумматор – логическая схема, которая способна суммировать 2 одноразрядных двоичных числа с переносом из предыдущего разряда.

Сумматор может находить применение и в других устройствах машины.
Для суммирования двоичных слов длиной от двух бит можно использовать последовательное соединение многоразрядных сумматоров, причём для двух соседних сумматоров выход переноса одного сумматора является входом для другого.
Пример реализации логической схемы

Алгоритм реализации:
-
Определим количество переменных данного выражения, значит столько входов будет иметь схема. В данном случае это входы $A, B, C$.
С помощью базовых логических элементов реализуются основные операции в порядке их следования:
I – инверсия переменных $A, B, C$ реализуется логическим элементом «НЕ»;
II – логическое умножение реализуется логическим элементом «И»;
III – логическое сложение реализуется логическим элементом «ИЛИ».
На выходе каждого элемента прописывается логическое выражение, которое реализуется данным элементом, что позволяет осуществить обратную задачу, т.е. по готовой схеме составить логическое выражение, которое реализует данная схема.
Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс — логический смысл сигнала — 1, нет импульса — 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции.Преобразование сигнала логическим элементом задается таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.

Логический элемент «И». На входы А и В логического элемента (рис. 3.1) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.
Pис. 3.1 Логический элемент • «И»

Логический элемент «ИЛИ». На входы А и В логического элемента (рис. 3.2) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.
Рис. 3.2 Логический элемент • "ИЛИ"

Логический элемент «НЕ». На вход А логического элемента (рис. 3.3) подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии
Рис. 3.3 Логический элемент • "НЕ"
Сумматор двоичных чисел
Из этой таблицы сразу видно, что перенос можно реализовать с помощью операции логического умножения:
Получим теперь формулу для вычисления суммы. Значения суммы близки к результату операции логического сложения (кроме случая, когда на входы подаются две единицы, а на выходе должен получиться нуль).
Нужный результат достигается, если результат логического сложения умножить на инвертированный перенос. Таким образом, для определения суммы можно применить следующее логическое выражение:
Теперь на основе полученных логических выражений можно построить из базовых логических элементов схему сложения одноразрядных двоичных чисел.
По логической формуле переноса легко определить, что для получения переноса необходимо использовать логический элемент «И».
Анализ логической формулы для суммы показывает, что на выходе должен стоять элемент логического умножения «И», который имеет два входа. На один из входов надо подать результат логического сложения исходных величин А и В, то есть на него должен подаваться сигнал с элемента логического сложения «ИЛИ».

На второй вход требуется подать результат инвертированного логического умножения исходных сигналов (А & В), то есть на второй вход должен подаваться сигнал с элемента «НЕ», на вход которого должен поступать сигнал с элемента логического умножения «И» (рис. 3.4).
Рис. 3.4. Полусумматор двоичных чисел
Данная схема называется полусумматором, так как реализует суммирование одноразрядных двоичных чисел без учета переноса из младшего разряда.
Перенос из младшего разряда
Идея построения полного сумматора точно такая же, как и полусумматора. Из таблицы сложения видно, что перенос (логическая переменная Р) принимает значение 1 тогда, когда хотя бы две входные логические переменные одновременно принимают значение 1. Таким образом, перенос реализуется путем логического сложения результатов попарного логического умножения входных переменных (А, В, ро). Формула переноса получает следующий вид:
Р = (А & В) v (А & Р0) v (В & Р0).
Для получения значения суммы (логическая переменная 5) необходимо результат логического сложения входных переменных (А, В,P0) умножить на инвертированный перенос Р:
S = (А v В v Р0) & !Р.
Данное логическое выражение дает правильные значения суммы во всех случаях, кроме одного, когда на все входные логические переменные принимают значение 1. Действительно:
S = (1v1v1)&!Р = 1 & 0 = 0.
Для получения правильного значения суммы (для данного случая переменная S должна принимать значение 1) необходимо сложить полученное выше выражение для суммы с результатом логического умножения входных переменных (А, В, P0). В результате логическое выражение для вычисления суммы в полном сумматоре принимает следующий вид:
S = (А v В v Р0) & !Р0 v (А & В & Р0). Многоразрядный сумматор. Многоразрядный сумматор процессора состоит из полных одноразрядных сумматоров. На каждый разряд ставится одноразрядный сумматор, причем выход (перенос) сумматора младшего разряда подключается ко входу сумматора старшего разряда.
Триггер
Важнейшей структурной единицей оперативной памяти компьютера, а также внутренних регистров процессора является триггер. Это устройство позволяет запоминать, хранить и считывать информацию (каждый триггер может хранить 1 бит информации).

Триггер можно построить из двух логических элементов «ИЛИ» и двух элементов «НЕ» (рис. 3.5).
Триггер
В обычном состоянии на входы триггера подан сигнал О, и триггер хранит 0. Для записи 1 на вход 5 (установочный) подается сигнал 1. Последовательно рассмотрев прохождение сигнала по схеме, видим, что триггер переходит в это состояние и будет устойчиво находиться в нем и после того, как сигнал на входе 5 исчезнет. Триггер запомнил 1, то есть с выхода триггера Q можно считать 1.Для того чтобы сбросить информацию и подготовиться к приему новой, подается сигнал 1 на вход К (сброс), после чего триггер возвратится к исходному «нулевому» состоянию.
Читайте также:


