Как составить маршрут в экселе
Главная Статьи Макросы Статьи Проекты Поиск кратчайшего маршрута
Поиск кратчайшего маршрута
При решении сложных алгоритмических задач с использование электронных таблиц иногда приходится сталкиваться с ошибками из-за возникновения циклических ссылок в расчетах. В подавляющем большинстве случаев эта ошибка связана с неверным построением формул. Но нередко цикл заложен в алгоритме решения задачи. Немногие знают, что Excel позволяет производить итерационные вычисления без использования макросов.
В примере к статье с помощью итерационных вычислений показано решение задачи по поиску кратчайшего маршрута в лабиринте. Задача, на первый взгляд, не совсем экономическая, но на практике может быть применена при оптимизации логистических и технологических процессов. В качестве другого популярного примера итерационных вычислений можно привести задачу распределения косвенных затрат при расчете полной себестоимости продукции. Здесь циклические вычисления возникают при распределении затрат вспомогательных служб: например, котельная использует электроэнергию, производимую в энергоцехе, который, в свою очередь, отапливается той же самой котельной. Совсем не обязательно решать подобную задачу распределения затрат через итерации, но знать потенциальные возможности Excel будет в любом случае нелишним.
Описание задачи
Итак, имеется карта лабиринта с предопределенными координатами входа и выхода. Карта представлена в виде прямоугольной таблицы, где каждая ячейка может быть либо стеной, либо проходом. По периметру имеется ограждение в виде стен, внутри стены могут располагаться произвольным образом. Единичный ход представляет собой шаг в одном из четырех направлений от текущей ячейки: вверх, вниз, вправо или влево. Требуется проложить кратчайший маршрут от входа к выходу.
Решение задачи
Настройка параметров Excel
В примере использованы формулы, работающие только с включенным режимом итерационных вычислений. Это режим устанавливается в параметрах Excel, в Excel 2000-2003 через меню Сервис\Параметры\Вычисления. В Excel 2007-2010 через диалог настройки общих параметров (раздел Формулы):
Кроме установки числа итераций (зависит от размера лабиринта), желательно установить ручной режим вычислений. В противном случае будет серьезно замедлен расчет при любом изменении исходных данных.
Также в примере установлен R1C1 режим отображения формул, что облегчает понимание алгоритмов при равнозначных по смыслу вертикальных и горизонтальных ссылках.
Алгоритм
Задача по поиску кратчайшего маршрута в лабиринте широко известна в математике и прикладном программировании. Общий смысл алгоритма можно изложить следующим образом:
1. Изначально все доступные для прохода ячейки очищаются. В дальнейшем в каждую ячейку проставляются номера шагов.
2. В ячейку «входа» устанавливается значение "1".
3. Цикл пока ячейка, обозначающая «выход», не заполнена номером. Выход из цикла также осуществляется, если за полный проход не было сделано никаких исправлений – в этом случае решения задачи нет.
3.1 Цикл по всем ячейкам
3.1.1 В каждую ячейку устанавливается минимальный номер из соседних и текущей ячейки плюс единица. При этом пустые соседние ячейки в сравнение не попадают.
4. При успешном результате оптимальным маршрутом является любая последовательность с последовательным увеличением номера на единицу от «входа» к «выходу».
Также популярным решением этой задачи является рекуррентный вызов процедуры перемещения из одной ячейки в другую до достижения выхода.
Формула
Любая ячейка внутри лабиринта на листе «Маршрут» содержит следующую формулу:
Формула очень сложная (в Excel 2000-2003 достигается максимум по уровням вложенных скобок внутри одной формулы) и требует дополнительных пояснений. Общий смысл на самом деле соответствует описанному ранее циклическому алгоритму. Т.е. определяется минимум из соседних ячеек. При этом «стены» (отрицательные значения) не обрабатываются за счет замены их значений на большое число (999).
Обратите внимание, на преимущество R1C1 адресации – сразу видно, что формула абсолютна одинаковая во всех ячейках. Без использования итерационных вычислений будет выдана ошибка - циклическая ссылка в формулах . Действительно, все соседние ячейки лабиринта ссылаются друг на друга.
Решение
После изменений в расположении стен и проходов на листе «Карта» требуется перейти на лист «Лабиринт» и запустить ручной пересчет Excel. Это проще всего сделать через нажатие клавиши F9. Карта отобразит начальный лабиринт и маршрут оптимального перемещения. Стены выделены серым цветом, маршрут - желтым.
Форматирование
Ячейки внутри лабиринта содержат формулы, и соответственно вычисленные значения. В примере эти значения скрыты – видим только цвет фона. Числа скрыты, во-первых, для простоты восприятия («для красоты»), во-вторых, чтобы продемонстрировать возможности специального формата Excel. Вызовите диалог формата ячейки (проще всего это делается через сочетание клавиш Ctrl+1):
Пользовательский формат «;;;» обозначает, что для положительных, отрицательных, нулевых и текстовых значений необходимо показывать пустую ячейку.
Для раскраски ячеек использованы условные форматы двух типов:
1. «Стены» вычисляются через формулу как значение «-1».
2. Ячейка попадает в оптимальный маршрут, если ее координата вычислена в служебной таблице. Здесь функция CELL("address"; RC) выводит адрес текущей ячейки в формате R1C1. Служебная таблица собирает координаты маршрута от «выхода» к «входу», используя целую и дробную часть каждой ячейки лабиринта.
Заключение
Расширение масштаба лабиринта требует копирования формул и добавления строк в служебную таблицу для показа маршрута. Обратите только внимание, что ячейка «входа» не содержит формулу – там значение первого шага (1,1). Также, вероятно потребуется увеличить параметр «Предельное число итераций». Будьте осторожны с увеличением размеров лабиринта - скорость расчетов будет замедляться в геометрической прогрессии.
Описанная в примере задача гораздо проще и элегантнее решается с помощью программы на VBA. Можно использовать как простые циклы, так и рекурсивные вызовы процедур. Вероятно, для тех, кто не очень «дружит» с программированием, приведенный пример решения задачи с помощью формул будет также непонятен. В любом случае, надеемся, что статья будет являться для вас дополнительным стимулом по изучению возможностей формул Excel и VBA.
Предположим, что перед нами стоит классическая задача транспортной логистики: визуализировать движение некоего объекта по заданному маршруту из нескольких промежуточных точек. Для конкретики, давайте возьмем скорый фирменный поезд "Жигули", движущийся по маршруту Москва - Самара по следующему графику (взято из Яндекс.Расписаний):

Для решения задачи нам потребуется Excel 2013-2016 с установленной надстройкой Power Map. В Excel 2016 она установлена по умолчанию, для Excel 2013 можно скачать ее бесплатную превью-версию.
Этап 1. Находим координаты
Для однозначной привязки к промежуточным пунктам маршрута лучше использовать не названия населенных пунктов (они могут повторяться либо отсутствовать в принципе в нужном месте), а нормальные географические координаты. Достаточно щелкнуть по нужному месту в Яндекс-картах или Google Maps и вы увидите широту и долготу этой точки:

Добавим найденные координаты к нашей исходной таблице расписания движения поезда:

Этап 2. Дробим перегоны
Для плавного отображения движения поезда на карте нам необходимо разделить каждый перегон на несколько участков (чем их больше, тем плавнее будет анимация). Таким образом, перед нами встает задача получить примерные координаты и время для каждой промежуточной точки. Решить проблему можно формулой либо макросом.
Например, если хотим разбить каждый перегон на шесть интервалов (т.е. пять точек), то можно реализовать все одной формулой:

Но вставлять промежуточные строки, вводить и копировать формулу на все зеленые ячейки для каждого перегона придется вручную.
Другой вариант - макрос, что гораздо удобнее при большом количестве перегонов и промежуточных точек маршрута. Откройте редактор Visual Basic на вкладке Разработчик (Developer) или нажмите сочетание клавиш Alt + F11 . Вставьте в вашу книгу новый пустой модуль через меню Insert - Module и скопируйте туда этот код:
Как легко сообразить, константа MINS_IN_ONE_STEP задает количество минут в каждом шаге - можете менять ее значение по своему усмотрению. Теперь если выделить таблицу с данными или установить в нее активную ячейку, а потом запустить наш макрос сочетанием клавиш Alt + F8 или кнопкой Макросы на вкладке Разработчик (Developer - Macros) , то наша таблица будет преобразована в следующий вид:

Как видите, каждый перегон теперь делится на несколько интервалов - по 1 минуте каждый.
Этап 3. Переходим к карте
Осталось совсем чуть-чуть. Выделите полученную таблицу и на вкладке Вставка нажмите кнопку 3D-карта (Insert - 3D-map) :

Не перепутайте ее с кнопкой Карты (которая с глобусом) или Карты Bing (желтого цвета). После нажатия должно открыться окно надстройки Power Map.
В правой части окна на панели добавьте в группе Расположение (Location) поля широты и долготы и выберите напротив каждого название соответствующего столбца из нашей таблицы. Если все сделаете правильно, то на карте тут же должен отобразиться наш маршрут:

Теперь осталось выбрать в выпадающем списке Время (Time) столбец со значениями даты-времени из нашей таблицы и можно запускать анимацию с помощью кнопки воспроизведения в нижней части окна:
Дополнительно можно поиграться настройками слоя - кнопка Параметры слоя (Layer Options) в правом нижнем углу - и установить цвет, размер, прозрачность и т.д. отображаемых точек.
Если нажать на неприметную иконку с часами рядом с выпадающим списком Время, то можно поменять режим отображения и рисовать не маршрут, а сам поезд.
При щелчке левой кнопкой мыши по любой интересующей точке маршрута мы увидим ее подробные данные - координаты и время прохождения:

Этап 4. Несколько поездов сразу
Не секрет, что на самом деле по маршруту Москва-Самара курсируют два состава - в противофазе: когда один стартует из Москвы, другой примерно в то же время начинает движение ему навстречу из Самары. Утром один из них приходит в Самару, а другой, соответственно, в Москву и вечером процесс запускается заново. Расписание второго примерно отзеркаливает первый:

Что сделать, чтобы отобразить их на карте оба сразу?
Если по маршруту одновременно движется больше одного объекта, то данные по ним можно обработать аналогичным образом (Этапы 1 и 2) и просто добавить в продолжение нашей маршутной таблицы. А чтобы отличать поезда друг от друга, добавить еще один столбец с названием объекта:

Теперь, если построить по такой таблице еще одну визуализацию, мы будем видеть движение двух составов одновременно:
Ссылки по теме

Николай,-очень кстати данная тема, работа связана с транспортом и маршрутами,давно ждал что то подобное.Огромное Вам спасибо
Просто прекрасная и нужная инструкция. Николай, коллеги, а подскажите, пожалуйста, какой модуль к MS Office должен быть подключен для того, чтобы было доступно:
Вставка ---> нажмите кнопку 3D-карта (Insert - 3D-map) :
"Для решения задачи нам потребуется Excel 2013-2016 с установленной надстройкой Power Map. В Excel 2016 она установлена по умолчанию, для Excel 2013 можно скачать ее бесплатную превью-версию ."



Очень крутая тема .
Предлагаю развить на предмет расчета расстояния.
Подскажите пожалуйста как это возможно реализовать с помощью google map например?
У меня есть вот такой макрос, который рассчитывает расстояние, маршрут и время в пути. Мне необходима только та часть которая отвечает за измерение расстояния. Самостоятельно разобрать не хватает знаний. Буду признателен за помощь.
Option Explicit
Public ActivationMark As Boolean
Public WasRequestGoogle As Boolean
Public MyDistance As Variant
Public MyDuration As Variant
'Задаем границы допустимых координат
Public Const Lat_min = -180, Lat_max = 180
Public Const Lon_min = -180, Lon_max = 180
'Скрываем заставку
Private Sub KillTheForm()
Unload Excelminsk
End Sub
Sub GetDistanceDurationGoogle(Address1 As String, Address2 As String)
Dim XMLDoc As Object
Dim Coord1NodeList As Object, Coord2NodeList As Object
Dim DistanceNodeList As Object, DurationNodeList As Object
Dim MyRequest As String
Dim Lat1 As String, Lon1 As String, Lat2 As String, Lon2 As String

Для решения транспортной задачи в EXCEL нам потребуется инструмент Поиск решения из меню Сервис. С помощью его можно искать решение систем уравнений, которые к тому же могут содержать ограничения. Если этого инструмента в меню нет, то его надо установить. Для этого в CD-привод ставим установочный диск Microsoft Office, затем в меню Сервис нажимаем на инструмент Надстройки… , в поле Доступные надстройки ставим галочку напротив инструмента Поиск решения (рисунок 1), далее нажимаем ОК . Далее выскочит окно нажимаем кнопку Да , и компьютер начнет устанавливать этот инструмент.
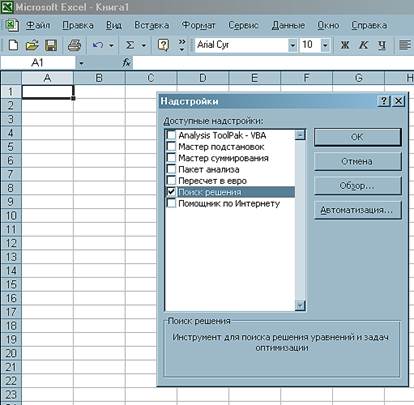
Рисунок 1 – Установка инструмента Поиск решения
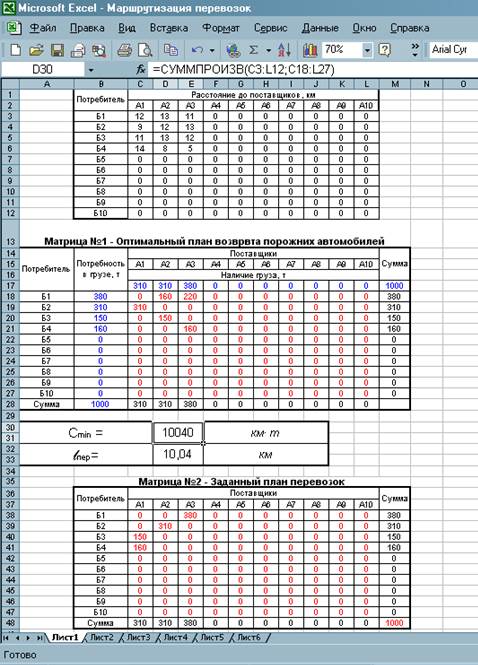
Рисунок 2 – Расстояния до поставщиков, оптимальный и заданный план перевозок
1. На первом листе размещаем в таблицы (матрица №2) сведения из заказов на перевозку и расстояния от поставщиков к потребителям, как показано на рисунке 2. Находим оптимальный план движения автомобилей без груза (матрица №1), т.е. кратчайший путь возврата порожних автомобилей на пункты погрузки, аналогично тому, как это было сделано ранее при определении оптимального плана закрепления потребителей за поставщиками.
2.Составление алгоритма решения первого маршрута
2.1. Составление совмещенной матрицы (матрица №3)
Накладываем данные одной матрицы на другую, как показано на рисунке 3 . Причем слева в ячейке ставим ссылку на матрицу №2 – план перевозок, а справа в ячейке на матрицу №1 – оптимальный план возврата порожних автомобилей. Например клетка матрицы №3 А1Б1:
– Слева в ячейке С4 листа 2 ставим знак «=», переходим на Лист 1, нажимаем мышкой на ячейку С38, нажимаем Enter, получаем запись в ячейке С4 листа 2:
Это означает что значение в ячейке С4 листа 2 равно значению ячейки С38 листа 1, и если мы поменяем значение в этой ячейке, то автоматически поменяется значение в С4 листа 2.
– Справа в ячейке D4 листа 2 ставим знак «=», переходим на Лист 1, нажимаем мышкой на ячейку С18, нажимаем Enter, получаем запись в ячейке D4 листа 2:
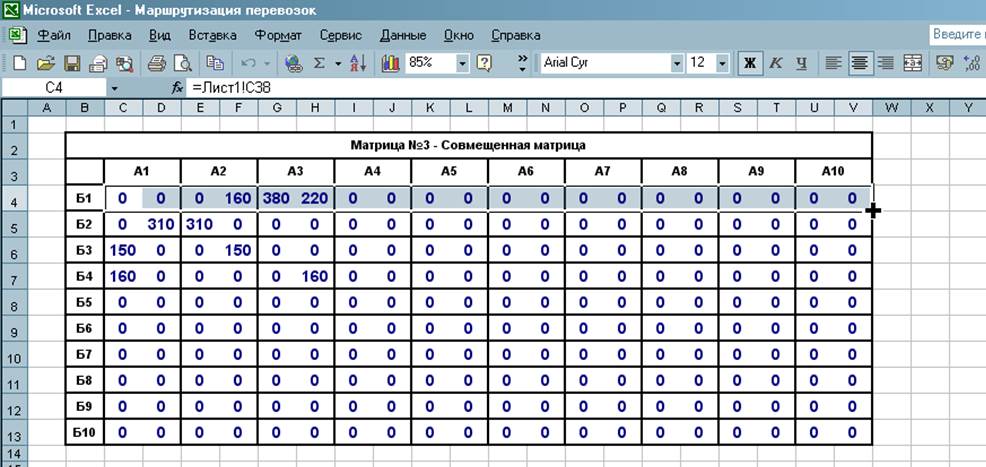
Рисунок 3 – Совмещённая матрица
Так заполняем все ячейки первой строки. Заполнение остальных ячеек делаем так: левой кнопкой мышки выделяем все ячейки первой строки, ставим курсор в левый нижний угол, что бы курсор принял вид «+», нажимаем и держим левую кнопку мыши, ведём мышкой до самой нижней строки, отпускаем кнопку. Таким образом, формулы из ячеек первой строки переносятся на остальные ячейки. Если в клетке матрицы находятся две цифры, то это и есть маятниковый маршрут.
2.2. Расчет маятниковых маршрутов
Для расчета маятниковых маршрутов составляем матрицу №4 (рисунок 4). Что бы выделить маятниковые маршруты нужно вывести минимальное число из каждой клетки совмещенной матрицы. Для этого нам потребуется функция МИН(число1;число2;…), она возвращает минимальное значений из списка аргументов. Для этого в ячейке С17 ставим знак «=», верхнем правом углу ищем значок fx , нажимаем его, откроется окно Мастер функций, в поле Категория выбираем Полный арифметический перечень, ищем функцию МИН, нажимаем ОК, откроется окно Аргументы функции, в строке Число1 нажимаем на значок , мышкой выделяем ячейку С4, нажимаем Enter, в строке Число2 нажимаем на значок , мышкой выделяем ячейки D4, нажимаем Enter, затем ОК, таким образом, мы записываем формулу в ячейке С17:
в ячейке D17 записываем формулу:
в ячейке E17 записываем формулу:
в ячейке F17 записываем формулу:
Так заполняем все ячейки первой стоки. Остальные ячейки заполняем, перенося формулы, как это было показано выше, получаем матрицу №4.
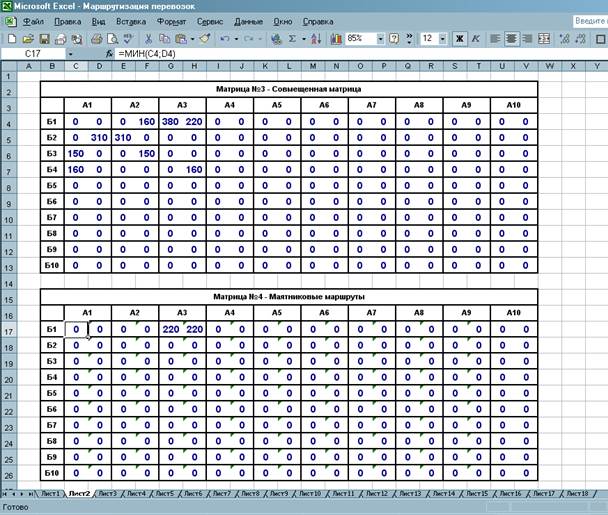
Рисунок 4 – Маятниковые маршруты
Таким образом, матрица №4 отображает количество груза, перевозимое в маятниковых маршрутах. Далее исключаем маятниковые маршруты из совмещенной матрицы. Для этого вычитаем из матрицы №3 матрицу №4 по каждой ячейке (рисунок 5). В ячейке С30 ставим знак «=», мышкой нажимаем на ячейку С4, ставим знак «-», мышкой нажимаем на ячейку С17, получаем запись
Переносим эту формулу сначала на всю строку, затем на всю матрицу. Таким образом, получаем матрицу №5.
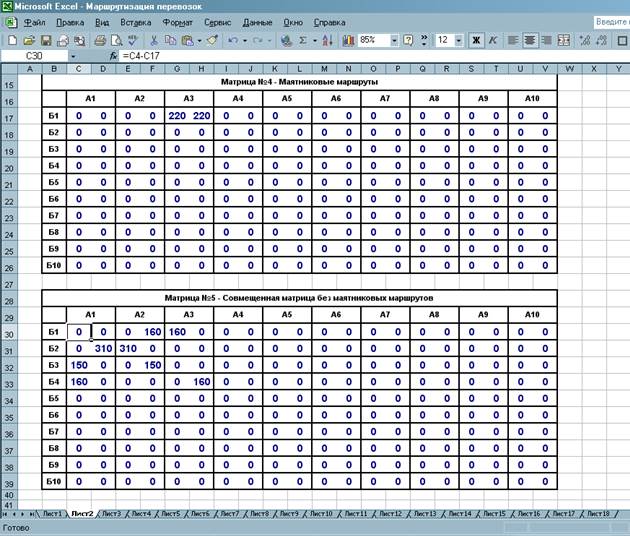
Рисунок 5 – Совмещенная матрица без маятниковых маршрутов
2.3. Составление поля изменяемых ячеек и ограничения для инструмента Поиск решения
Составляем вспомогательную матрицу (рисунок 6). В ячейке С44 записываем формулу
в ячейке D44 записываем формулу
Так заполняем первую строку, на остальные строки переносим формулы. Таким образом, получаем матрицу №6.
Находить маршрут будем в двоичной системе, то есть «1» означает вершину контура маршрута в клетке матрицы, «0» означает, что вершины контура в клетке нет. Для того чтобы все цифры вспомогательной матрицы перевести в двоичную систему нам потребуется функция ЗНАК(число). Она возвращает знак числа: 1 – если число положительное, 0 – если оно равно нулю и -1 – если число отрицательное.
Для этого в ячейке N44 записываем формулу:
Переносим формулу сначала на всю строку, а затем на всё матрицу. Таким образом, получаем матрицу №7
Для заданного плана из совмещенной матрицы без маятниковых маршрутов (рисунок 5) берём цифры слева клетки, то есть в ячейке С58 записываем формулу:
в ячейке D58 записываем формулу:
И так, заполняем все ячейки первой строки, затем формулы из первой строки переносим на всю матрицу, получаем матрицу №8.
А для оптимального плана из совмещенной матрицы берём цифры справа клетки, то есть в ячейке N58 записываем формулу:
в ячейке O58 записываем формулу:
Так, заполняем все ячейки первой строки, затем формулы из первой строки переносим на всю матрицу, получаем матрицу №9.
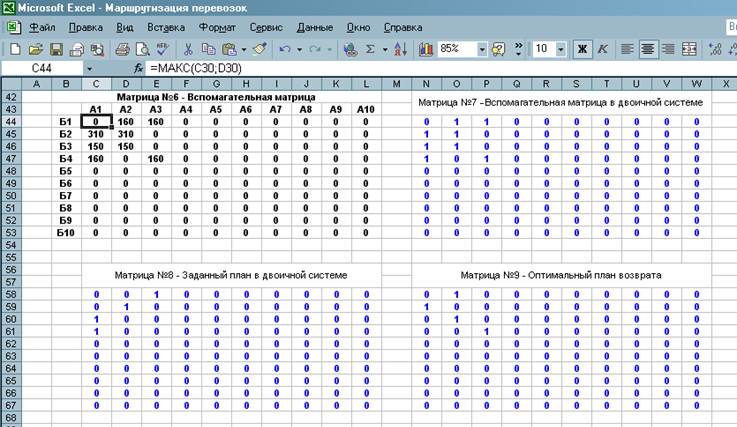
Рисунок 6 – Вспомогательная матрица, заданный план и оптимальный план возврата в двоичной системе
Матрицы №8 и №9 будут являться ограничениями для инструмента Поиск решения.
Составим поле изменяемых ячеек (рисунок 7).
В этом поле программа вычертит контур маршрута, то есть будет ставить в каждой клетке либо «1» либо «0». Чтобы обеспечить чередование цифр из оптимального плана возврата и заданного плана в контуре, поле изменяемых ячеек разбиваем на две половины. Верхняя (ячейки C71;L80) будет отображать вершины контура маршрута из заданного плана, а нижняя (ячейки C81;L90) из оптимального плана возврата.
Раскрываем меню Сервис, открываем инструмент Поиск решения:
Эксель можно использовать для решения широкого спектра задач, в том числе, для нахождения наилучшего способа осуществления перевозок от производителя (продавца) к потребителю (покупателю). Давайте посмотрим, каким образом это можно реализовать в программе.
Транспортная задача: описание
С помощью транспортной задачи можно найти наилучший вариант перевозки с минимальными издержками между двумя взаимодействующими контрагентами (в рамках данной статьи будем рассматривать покупателей и продавцов). Чтобы приступить к решению, нужно представить исходные данные в схематичном или матричном виде. Последний вариант применяется в Эксель.
Транспортные задачи бывают двух типов:
- Закрытая – совокупное предложение продавца равняется общему спросу.
- Открытая – спрос и предложение не равны. Чтобы решить такую задачу, нужно сначала привести ее к закрытому типу. В этом случае добавляется условный покупатель или продавец с недостающим количеством спроса или предложения. Также в таблицу издержек следует внести соответствующую запись (с нулевыми значениями).
Подготовительный этап: включение функции “Поиск решения”
Чтобы решить транспортную задачу в Эксель, нужно воспользоваться функцией “Поиск решения”, которую нужно предварительно активировать, т.к. изначально она не включена. Алгоритм действий следующий:
Пример задачи и ее решение
Чтобы лучше понять, как решать транспортные задачи в Excel, давайте рассмотрим конкретный практический пример.
Условия задачи
Допустим, у нас есть 6 продавцов и 7 покупателей. Предложение продавцов составляет 36, 51, 32, 44, 35 и 38 единиц. Спрос покупателей следующий: 33, 48, 30, 36, 33, 24 и 32 единицы. Суммарные количества по спросу и предложению равны, следовательно, это транспортная задача закрытого типа.

Также, мы имеем данные по издержкам перевозок из одного пункта в другой (ячейки с желтым фоном).

Алгоритм решения
Итак, приступи к решению нашей задачи:
- в поле для ввода значения напротив первого аргумента “Массив1” указываем координаты диапазона ячеек матрицы затрат (с желтым фоном). Сделать это можно, используя клавиши на клавиатуре, или просто выделив нужную область в самой таблице с помощью зажатой левой кнопки мыши.
- в качестве значения второго аргумента “Массив2” указываем диапазон ячеек новой таблицы (либо вручную, либо выделив нужные элементы на листе).
Заключение
Таким образом, с помощью программы Эксель достаточно просто решить транспортную задачу. Самое главное – правильно заполнить начальные данные и четко следовать плану действий, и тогда проблем быть не должно, т.к. программа все расчеты выполнит сама.
Читайте также:


