Как сохранить файл в скайлабе
file – строка, в которой хранится имя файла, mode – режим работы с файлом:
● ' r ' открываемый текстовый файл доступен для чтения,
● ' rb ' открываемый двоичный файл доступен для чтения,
● ' w ' – создаваемый пустой текстовый файл предназначен только для записи информации;
● ' wb ' – создаваемый пустой двоичный файл предназначен только для записи
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab
● ' a ' – открываемый текстовый файл будет использоваться для добавления данных
в конец файла; если файла нет, он будет создан;
● ' ab ' – открываемый двоичный файл будет использоваться для добавления данных
в конец файла; если файла нет, он будет создан;
● ' r+ ' – открываемый текстовый файл используется в режиме чтения и записи;
● ' rb+ ' – открываемый двоичный файл используется в режиме чтения и записи;
● ' w+ ' – создаваемый пустой текстовый файл предназначен для чтения и записи информации;
● ' wb+ ' – создаваемый пустой двоичный файл предназначен для чтения и записи информации;
● ' a+ ' – открываемый текстовый файл будет использоваться для добавления данных
в конец файла и чтения данных; если файла нет, он будет создан;
● ' ab+ ' – открываемый двоичный файл будет использоваться для добавления данных в конец файла и чтения данных; если файла нет, он будет создан.
9.3.2. Функция записи в текстовый файла fprintf
Функция записи в текстовый файл mfprintf имеет вид mfprintf(f, s1, s2) .
Здесь f – идентификатор файла (значение идентификатора возвращается функцией fopen ), s1 – строка вывода, s2 – список выводимых переменных.
В строке вывода вместо выводимых переменных указывается строка преобразования следующего вида:
Значения параметров строки преобразования приведены в таблице 9.1.
умолчанию выравнивание вправо.
Перед числом выводится знак «+» или «-»
Перед положительным числом выводится
пробел, перед отрицательным – «-»
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab
перед восьмеричным числом, 0х (0Х) пе-ред
Ширина поля вывода. Если n позиций
недостаточно, то поле вывода расширяется до
минимально необходимого. Незаполненные
позиции заполняются пробелами.
То же, что и n, но незаполненные позиции
Точность по умолчанию
Для типов e, E, f выводить n знаков после
Для d, i, o, u, x, X короткое целое
Для d, i, o, u, x, X длинное целое
При вводе символьный тип char, при
выводе один байт.
Десятичное со знаком
Десятичное со знаком
Восьмеричное int unsigned
Десятичное без знака
Шестнадцатеричное int unsigned, при х
используются символы a-f, при Х – A-F.
Значение со знаком вида [-]dddd.dddd
Значение со знаком вида [-]d.dddde[+|-]ddd
Значение со знаком вида [-]d.ddddE[+|-]
Значение со знаком типа e или f в
зависимости от значения и точности
Значение со знаком типа E или F в
зависимости от значения и точности
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab
В строке вывода могут использоваться некоторые специальные символы, приведенные
Некоторые специальные символы
Сдвиг текущей позиции влево
Перевод в начало строки, не переходя на
Символ одинарной кавычки
Символ двойной кавычки
9.3.3. Функция чтения данных из текстового файла fscanf
При считывании данных из файла можно воспользоваться функцией mfscanf следующего вида
Здесь f – идентификатор файла, который возвращается функцией mopen, s1 – строка форматов вида
Функция mfscanf работает следующим образом: из файла с идентификатором f считываются в переменную A значения в соответствии с форматом s1 . При чтении числовых значений из текстового файла следует помнить, что два числа считаются разделенными, если между ними есть хотя бы один пробел, символ табуляции или символ перехода на новую строку.
При считывании данных из текстового файла пользователь может следить, достигнут ли конец файла с помощью функции meof(f) ( f – идентификатор файла), которая возвращает единицу, если достигнут конец файла, и ноль в противном случае.
9.3.4 Функция закрытия файла mclose
После выполнения всех операций с файлом он должен быть закрыт с помощью функции mclose следующей структуры
Здесь f – идентификатор закрываемого файла. С помощью функции mclose('all') можно
Алексеев Е.Р., Чеснокова О.В. Программирование в Scilab
закрыть сразу все открытые файлы, кроме стандартных системных файлов. Пример создания текстового файла приведен на листинге 9.15.
A=[2 4 6 7; 6 3 2 1; 11 12 34 10]; f=mopen('E:\abc.txt','w'); fprintf(f,'%d\t%d\n',N,M);
for i=1:N for j=1:M
Листинг 9.15.Создание текстового файла
Созданный текстовый файл можно .увидеть на рис. 9.18
Рис. 9.18. Тестовый файл
Пример чтения данных из этого текстового файла приведен на листинге 9.16. f=mopen('E:\abc.txt','r');
M=mfscanf(f,'%d'); for i=1:N
for j=1:M A(i,j)=mfscanf(f,'%g'); end
Листинг 9.16.Чтение из текстового файла
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Завтра мне сдавать экзамен по такому предмету как КСВЭ(Компьютерный сервис вычислительного эксперимента). А лучший способ подготовки — это написание статьи. Я рассмотрю часть вопросов к экзамену, которые связаны с SciLab.
Статья больше подходит для студентов, использующих scilab для проверки решения, для или для сдачи экзамена по дисциплине КСВЭ. Для более подробного изучения надо читать литературу, указанную в конце статьи
Основные термины
Scilab (читается Сайлэб) — пакет прикладных математических программ, предоставляющий мощное открытое окружение для инженерных (технических) и научных расчётов.
CeCILL (от «CEA CNRS INRIA Logiciel Libre») — это лицензия на свободное программное обеспечение, адаптированная к интернациональному законодательству и законодательству Франции, подобная GNU General Public License и сохраняющая совместимость с ним.
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛА́У) в линейной алгебре — это система уравнений вида
Обыкнове́нные дифференциа́льные уравне́ния (ОДУ) — это дифференциальное уравнение вида
где — неизвестная функция (возможно, вектор-функция, тогда, как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной, штрих означает дифференцирование по. Число (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1)
1. Система компьютерной математики SciLab: История разработки. Возможности и ключевые особенности. Достоинства и недостатки.
История
С 1994 года распространяется вместе с исходным кодом через Интернет. В 2003 году для поддержки Scilab был создан консорциум Scilab Consortium. Сейчас в него входят 25 участников, в том числе Mandriva, INRIA и ENPC (Франция).
Возможности
Scilab содержит сотни математических функций, и есть возможность добавления новых, написанных на различных языках (C, C++, Fortran и т. д.). Также имеются разнообразные структуры данных (списки, полиномы, рациональные функции, линейные системы), интерпретатор и язык высокого уровня.
Scilab был спроектирован как открытая система, и пользователи могут добавлять в него свои типы данных и операции путём перегрузки.
В системе доступно множество инструментов:
2D и 3D графики, анимация
Линейная алгебра, разреженные матрицы (sparse matrices)
Полиномиальные и рациональные функции
Интерполяция, аппроксимация
Симуляция: решение ОДУ и ДУ
Scicos: гибрид системы моделирования динамических систем и симуляции
Дифференциальные и не дифференциальные оптимизации
Обработка сигналов
Параллельная работа
Статистика
Работа с компьютерной алгеброй
Интерфейс к Fortran, Tcl/Tk, C, C++, Java, LabVIEW
Scilab имеет схожий с MATLAB язык программирования. В состав пакета входит утилита, позволяющая конвертировать документы Matlab в Scilab.
Scilab позволяет работать с элементарными и большим числом специальных функций (Бесселя, Неймана, интегральные функции), имеет мощные средства работы с матрицами, полиномами (в том числе и символьно), производить численные вычисления (например, численное интегрирование) и решение задач линейной алгебры, оптимизации и симуляции, мощные статистические функции, а также средство для построения и работы с графиками.
Для численных расчётов используются библиотеки Lapack, LINPACK, ODEPACK, Atlas и другие.
В состав пакета также входит Scicos — инструмент для редактирования блочных диаграмм и симуляции (аналог simulink в пакете MATLAB). Имеется возможность совместной работы Scilab с программой LabVIEW.
Ключевые особенности
Отличия от некоторых коммерческих программ:
Бесплатность.
Свободность (с версии 5.0).
Маленький размер — дистрибутив 4 версии занимал менее 20 МБ против более чем двухгигабайтного пакета MATLAB. Инсталлятор 5 версии (5.4.0) увеличился в объёме до 108 МБ.
Возможность запуска в консоли без использования графического интерфейса, в том числе в версии под Windows (в UNIX и Windows версиях MatLab-а эта возможность присутствует тоже). Это позволяет производить автоматизированные вычисления, есть пакетный режим.
Достоинства и недостатки
Поиски достоинства и недостатков на просторе интернета ни чего не дали. Так что расскажу о том, что я заметил сам.
Если говорить о достоинствах, тут самым основным для меня является бесплатность данного пакета, по сравнению с той же Mathematic, когда для выполнения лабораторных работы приходилось искать серийник или crack. Далее — это кросплатформеность, т.к. я больше предпочитаю использовать Gentoo, чем Windows. В принципе большенство достоинств описано в пункте Ключевые особенности.
Из недостатков я вижу только 2: Это нет такой визуализации программирования как в Mathematic, а так же система использует прежде всего численные подходы, для вычисления, что может сказаться на точности.
2. Основы работы в SciLab. Пользовательские и системные переменные. Математические выражения. Коментарии

Прежде чем перейти дальше, рассмотрим сам интерфейс. При запуске открывается командное окно.
Есть 2 варианта работы: 1 — это работа в том же командном окне, 2 — открыть SciNotes(что-то вроде блокнота с подсветкой) где можно написать код, который позднее запустить, результат выполнения появится в командном окне.
Для примера я рассмотрю вывод Hellow world.

Командная строка. Используем функцию вывода на дисплей disp()
При работе в SciNotes вы получите что то похожее
для выполнения кода, надо или нажать на стрелочку в право :) (как во многих средах разработки)
или Выполнение->… без отображение команд
в принципе можно использовать и другие методы выполнения, и не использовать вывод на экран
Результатом выполнения будет:
т.к. можно сказать что интерфейс изучен, далее я буду приводить просто код и результат выполнения
SciLab чувствителен к реестру, т.е. А и а — разные переменные переменные.
a=1,A=3
//Каждая операция начинается с новой строки или через запятую
//коментарии можно оставлять после двух символоф слэш
b=3
c=a+b
disp©
Основные операции:
+ сложение
— вычитание
* умножение
/ деление справа, т.е. x/y = xy^(-1)
\ деление слева, т.е. x\y = x^(-1)y
^ возведение в степень, т.е. x^y
** возведение в степень (эквивалентно ^)
’ эрмитово сопряжение (комплексное сопряжение и транспонирование)
3. Основы работы в SciLab. Функции и их типы. Способы объявления пользовательских функций. Использование функций. Файлы-сценарии и их применение для хранения функций.
Элементарные математические функции.
acos acosd acosh acoshm acosm acot acotd acoth
acsc acscd acsch asec asecd asech asin asind
asinh asinhm asinm atan atand atanh atanhm atanm
cos cosd cosh coshm cosm cotd cotg coth
cothm csc cscd csch sec secd sech sin
sinc sind sinh sinhm sinm tan tand tanh
tanhm tanm
exp expm log log10 log1p log2 logm max
maxi min mini modulo pmodulo sign signm sqrt
sqrtm
iconvert преобразование к целочисленному представлению
inttype определение типа целого числа
простейший способ вызова пользовательской функции:
пример пользовательской фунции:
function y = myfunction ( x )
y = 2 * x
endfunction
Сохраняем её. Далее приведён пример вызова данной функции
-->exec('D:\PRIVATE\Учёба\КСВЭ\myfunction.sci', -1)
-->y = myfunction ( 3 )
y =
4. Определение одномерный и многомерных массивов. Основные действия над массивами.
Пример, как задаётся одномерный массив:
квадратные скобки ”[” и ”]” обозначают начало и конец перечисления
элементов матрицы,
запятой ”,” отделяются элементы матрицы, находящиеся в одной строке,
точка с запятой ”;” разделяет строки матрицы.
size определить размер матрицы
matrix изменить размер матрицы
resize_matrix создать новую матрицу заданного размера и скопировать
в нее элементы из исходной матрицы
Операции над матрицами:
Обращение к элементам матрицы
i = 1; 2, а j = 3; 4
для этого возьмём уже готовую матрицу
-->A = testmatrix (" hilb ", 5)
A =
25. — 300. 1050. — 1400. 630.
— 300. 4800. — 18900. 26880. — 12600.
1050. — 18900. 79380. — 117600. 56700.
— 1400. 26880. — 117600. 179200. — 88200.
630. — 12600. 56700. — 88200. 44100.
-->A(1: 2, 3: 4)
ans =
1050. — 1400.
— 18900. 26880
A матрица целиком
A(. ) матрица целиком
A(i:j,k) элементы матрицы в k-ом столбце с i-ой по j-ую строку
A(i,j:k) элементы матрицы в i-ой строке с j-ого по k-ый столбец
A(i,:) i-ая строка матрицы
A(:,j) j-ый столбец матрицы
Генерация единичной матрицы
Операции над матрицами
+ сложение .+ поэлементное сложение
— вычитание .- поэлементное вычитание
* умножение .* поэлементное умножение
/ деление справа ./ поэлементное деление справа
\ деление слева .\ поэлементное деление слева
^ или * возведение в степень :^ поэлементное возведение в степень
’ эрмитово сопряжение (комплексное сопряжение и транспонирование)
.’ транспонирование без сопряжения
пример умножения числа на еденичную матрицу 2 на 2
5. Определение одномерный и многомерных массивов. Специальные матричные функции
функции работы с матрицами
chol разложение Холесского
companion сопровождающая матрица
cond число обусловленности
det определитель матрицы
inv обратная матрица
linsolve решение систем линейных уравнений
lsq метод наименьших квадратов
lu LU-разложение с выбором опорного элемента
qr QR-разложение
rcond обратное число обусловленности
spec собственные значения и векторы
svd разложение по сингулярным числам матрицы
testmatrix генерация специальных матриц (Гильберта, Франка и др.)
trace след матрицы
6. Определение одномерный и многомерных массивов. Решение СЛАУ. Символьные массивы и операции над ними
Текст файла–сценария с решением задачи по формулам Крамера
-->A=[2 1 -5 1;1 -3 0 -6;0 2 -1 2;1 4 -7 6];//Матрица коэффициентов
-->b=[8;9;-5;0]; //Вектор свободных коэффициентов
-->//Первая вспомогательная матрица
-->A1=A;A1(:,1)=b;
-->//Вторая вспомогательная матрица
-->A2=A;A2(:,2)=b;
-->//Третья вспомогательная матрица
-->A3=A;A3(:,3)=b;
-->//Четвертая вспомогательная матрица
-->A4=A;A4(:,4)=b;
-->//Главный определитель отличен от нуля
-->D=det(A);
-->//Определители вспомогательных матриц
-->d(1)=det(A1);
-->d(2)=det(A2);
-->d(3)=det(A3);
-->d(4)=det(A4);
-->//Вектор неизвестных
-->x=d/D
x =
3.
— 4.
— 1.
1.
-->//Проверка
-->P=A*x-b
P =
0.
0.
— 8.882D-16
2.665D-15
-->A=[2 -1 1;3 2 -5;1 3 -2];
-->b=[0;1;4];
-->//Приведение расширенной матрицы к треугольному виду
-->C=rref([A b]);
-->//Выделение последнего столбца из матрицы,
-->//x — решение системы
-->x=C(1:3,4:4)
x =
0.4642857
1.6785714
0.75
-->A*x //Проверка
ans =
— 5.551D-16
1.
4.
7. Численное интегрирование. Подходы к интегрированию. Интегрирование функций заданных пользователем
Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла (как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.
Интегрирование по методу трапеций
проинтегрируем функцию, корень из 2*x-1 на отрезке от 1 до 10 с разбиением в 1 шаг
-->x=1:10
x =
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
-->y=sqrt(2*x-1)
y =
column 1 to 6
1. 1.7320508 2.236068 2.6457513 3. 3.3166248
column 7 to 10
3.6055513 3.8729833 4.1231056 4.3588989
-->inttrap(x,y)
ans =
27.211585
Квадратурные формулы Ньютона Котеса
8.Численное дифференцирование. Подходы к дифференцированию.
Численное дифференцирование — совокупность методов вычисления значения производной дискретно заданной функции.
В основе численного дифференцирования лежит аппроксимация функции, от которой берется производная, интерполяционным многочленом. Все основные формулы численного дифференцирования могут быть получены при помощи первого интерполяционного многочлена Ньютона (формулы Ньютона для начала таблицы).
в точке
-->function f=myf(x), f=(x+2)^3+5*x, endfunction;
-->numdiff(myf,1)
ans =
32.
-->x=1;3*(x+2)^2+5
ans =
32.
v=0:3;
-->numdiff(my,v)
ans =
17. 0. 0. 0.
0. 32. 0. 0.
0. 0. 52.999999 0.
0. 0. 0. 80.000002
-->function f1=my1(x), f1=3*(x+2)^2+5, endfunction;
-->my1(v)
ans =
17. 32. 53. 80.
9. Решение ОДУ средствами SciLab. Функции применяемые для решение ОДУ. Решение краевых задач.
Существует 4 способа для решения ОДУ:
1. С помощью команды ode, которая является солвером для решения обыкновенного
дифференциального уравнения.
2. С помощью команды odedc, которая вычисляет решение смешанной дискретно-
непрерывной системы.
3. Команда dassl, которая дает решение неявно выраженного дифференциального уравнения.
4. С помощью команды impl, которая дает решение неявно выраженного линейного
дифференциального уравнения.
-->y0=1;
-->t0=1;
-->t=1:0.01:1.5;
-->deff("[ydot]=f(t,y)",«ydot=y^(1/3)*t»)
-->y=ode(y0,t0,t,f);
-->y_exact=((t^2+2)/3)^(1.5);// это функция точного решения для сравнения
-->my_er=y-y_exact;
-->plot(t,y-y_exact) // это график ошибки вычисления от аргумента t

результатом является такой график
за одно можно увидеть Графическое окно. Построение графиков будет подробно рассмотрено далее.
10. Построение двухмерных графиков в системе SciLab. Основные функции и типы графиков.
Функция plot
рассмотрим пример:
как можно заметить первый параметр функции — это отрезок, а второй функции
так же существует возможность нарисовать сразу несколько функций, если их перечислить:

Функция plot2d
Рассмотрим функцию опять на примере:
x=[-2*%pi:0.1:2*%pi];
y=[sin(x); cos(x)];
plot2d(x,y',style=[color(«red»),color(«blue»)],rect=[-8,-2,8,2])

как мы можем увидеть, у этой функции намного больше функционала.
фунции передаются сразу массивом, так же можно указать цвет линий и отрезок.
Функция polarplot
Служит для построения графика в полярных координатах
fi=0:0.01:2*%pi;
ro=3*cos(5*fi);
ro1=3*cos(3*fi);
polarplot(fi,ro,style=color(«red»));

получается ромашка
параметры похожи как и в случае с plot2d
11. Построение трёхмерных графиков в системе SciLab. Основные функции и типы графиков.
Существует 4 способа построение графика:
Способ 1.
С помощью команды plot3d. Команда создает 3D график по точкам, заданным матрицами
x, y и z.
Способ 2.
С помощью команды plot3d1. Команда создает 3D график по точкам, заданным
матрицами x, y и z с помощью уровней цвета. Вещь в общем избыточная: величина
координаты z дополнительно еще и покрашена, в зависимости от принимаемого значения
z.
Способ 3.
С помощью команды fplot3d. Это аналог команды fplot3d, но изображаемая поверхность
задана с помощью внешней функции.
Способ 4.
С помощью команды fplot3d1. Это аналог команды plot3d1, но изображаемая поверхность
задана с помощью внешней функции.
Синтаксис этих команд смотри с помощью help.

забыл указать, что в графическом окне есть возможность экспорта данных, т.е. сохранить картинку

deff('[z]=surf(x,y)','z=sin(x)*cos(y)');
t=-%pi:0.3:%pi;
fplot3d(t,t,surf,35,45,«X@Y@Z»);
Результат такой же как в примере 1
deff('[z]=surf(x,y)','z=sin(x)*cos(y)');
t=-%pi:0.3:%pi;
fplot3d1(t,t,surf,35,45,«X@Y@Z»);
результат такой же, как в примере 2
12. Задача полиномов в SciLab. Символьные операции с полиномами. Решение алгебраический уравнений. Сравнение функций fsolve и roots.
Рассмотрим на примере решения уравнения 2x^4-8x^3+8x^2-1=0

В массиве указываются коэффициенты при х
После построения полинома, попробуем получить решение:
X=roots(p)
X =
2.306563
1.5411961
— 0.3065630
0.4588039

Для решения трансцендентных уравнений в применяют функцию Scilab fsolve(x0,f)
задача
Надеюсь данная статья послужит толчком, для дальнейшего изучения SciLab или решения своих задач/лабараторных
В этом разделе мы познакомимся с интерфейсом пользователя. Пользовательский интерфейс мы рассмотрим из-под Windows (пусть это вас не пугает, так как принципы едины во всех операционных системах). На рисунке 1 показан интерфейс программы, начиная с версии 5.4.
На рисунке 1 вы можете наблюдать, что внутри большого окна располагается ещё 4 более мелких:
- Обозреватель файлов;
- Командное окно;
- Обозреватель переменных;
- Журнал команд.
В каждый момент времени активным может быть только одно из видимых окон и признаком этого служит подсвеченный заголовок. На рисунке 1 активным является окно Командное окно. Отметим, что все окна не привязаны жёстко друг к другу и могут быть исключены из основного окна или заново перегруппированы.
Условно назовём вид, представленный на рисунке 1, группой окон. В любой момент каждое окно может быть исключено из группы путём нажатия на командную кнопку Исключить (англ. Undock ), которая представлена в виде кнопки со стрелочкой, стоящей между кнопками Справка (англ. Help on component ) и Закрыть (англ. Close ) на заголовке окна (см. рисунок 1). После исключения, окно может быть перемещено в любую точку рабочего стола.
Чтобы перегруппировать окна, необходимо ухватить заголовок окна, зажимая левую кнопку мышки, и перетащить курсор в желаемую позицию. «Фантом» в виде серой рамки будет подсказывать как встанет окно, если вы отпустите левую кнопку мыши, и здесь возможны следующие варианты:
- если вы попали курсором в какое-то окно группы, то перемещаемое окно поделит область по горизонтали пополам и займет свою позицию;
- то же, что и в предыдущем пункте, но по вертикали;
- окно не будет ничего разбивать, а просто вложится. В этом случае внизу появятся вкладки.
Исключённое окно может быть включено в любую группу. Для этого нужно захватить её заголовок и выполнить те же действия. Очень важно то, что хватать нужно не внешний заголовок окна, который генерируется операционной системой, а внутренний заголовок, на котором есть элементы управления Справка, Исключить и Закрыть.
Перегруппировка требует практики, так как тот или иной вариант будет предложен в определенной позиции курсора. Попрактикуйтесь немного и выполните следующее упражнение.
- Сделайте активным Командное окно;
- Введите команду

Вы могли убедиться, когда переключались между окнами, что среда обладает незамысловатым интерфейсом и содержит минимум элементов, что идёт только в плюс программе. Переключаясь на определенное окно вы можете заметить, что изменяется панель с инструментами группы и строка меню под это окно. В целом нет надобности расписывать каждую кнопку, так как всё интуитивно просто и понятно. Рекомендую читателю посмотреть все настройки, которые предоставляются пользователю в графическом режиме. Для этого:
- Сделайте активным Командное окно;
- Затем вверху выберите Правка (англ.Edit );
- В раскрывшемся меню нажмите на Настройки.
Коротко рассмотрим назначение каждого окна.
Командное окно — самое главное окно, посредством которого происходит общение со средой. В данное окно пользователь вводит команды и получает результаты.
На рисунке 1 в командном окне можно наблюдать техническую информацию о загрузке окружения, после которой система приглашает пользователя ввести команду. Начало строчки сопровождается стрелкой, указывающей направо (-->), которая и называется приглашением (англ. prompt или command prompt). Попробуйте ввести следующий код
В ответ от интерпретатора вы получите следующее
Другими словами, вы передали среде алгебраическое выражение, которое было ей рассчитано, а результат помещён в автоматически создаваемую переменную ans, с которой мы познакомимся позднее. Введя эту команду, вы внесли переполох в оставшихся окнах.
Перед тем как мы перейдём на следующее окно, введите вторую команду.
Этой командой вы попросили среду выделить память под новую переменную с именем myVariable и присвоить ей значение 26. Обратите внимание на точку с запятой в конце команды. Введя этот символ, вы попросили интерпретатор не выводить информацию о результате, получаемом после команды, к которой приставляется точка с запятой.
Например, попробуйте ввести
и вы получите ответ, что присваивание прошло
Блокирование вывода результата бывает полезным в случаях, когда результат оказывается очень большим, тривиальным или неудобным для изучения.
Это окно появилось относительно недавно и призвано облегчить работу с объектами, которые создал пользователь. Если вы попробовали ввести предыдущие команды, то можете наблюдать результат, показанный на рисунке 2.
В этом окне отображается вся необходимая информация о созданных переменных в частности:
- имя переменной;
- размер переменной;
- тип переменной или другими словами тип данных, которая эта переменная в настоящий момент хранит;
- видимость переменной.
Нажав по переменной дважды откроется окно редактора переменных, которое показано на рисунке 3.
Редактор переменных — это ещё одно новшество. Вероятно вы спросите, почему в редакторе переменная представлена таблицей, на что вам будет дан вполне внятный ответ:
Все объекты в среде Scilab являются двухмерными массивами, в лучших традициях MATLAB, частичной копией которого является Scilab.
Переменные, которые были нами созданы ранее, являются просто-напросто вырожденным случаем — массивом с одним элементом. Мы ещё не раз вернемся к этому вопросу, а пока внимательно рассмотрите редактор переменных.
На рисунке 3 показана переменная myVariable, которой было присвоено значение 26. Поменяйте значение переменной дважды щёлкнув по значению 26 и введя, к примеру, 51, а затем нажмите клавишу <Enter> или щёлкните в любом другом месте окна.
О том, что значение переменной изменилось, вы уже можете узнать из командной строки. Сделайте активным окно командной строки и введите имя нашей переменной, т.е.
Конечно показанный способ редактирования переменной является не самым рациональным, так как редактировать массив с одним полем проще всего из той же командной строки. Редактор же используется в случаях, когда необходимо редактировать большие массивы.
Не бойтесь, если вы пока ничего не понимаете. Мы ещё не раз вернемся ко всем этим вопросам.
Всё, что вы сейчас видите в этом окне — вершина айсберга. За этой вершиной скрывается ещё целая куча системных переменных, которые регулируют работу окружения и часть которых пользователь может контролировать. Чтобы их увидеть в окне, сделайте следующее:
- Сделайте активным окно Обозреватель переменных;
- На панели меню вверху выберите пункт Фильтр (англ.Filter );
- В раскрывшемся меню снимите галочку с пункта Скрывать системные переменные.
Рассмотрите эти переменные, но ни в коем случае не пробуйте их редактировать.
Окно журнала команд отражает все команды, которые вводил пользователь в командную строку в течении текущего сеанса. На рисунке 4 показано окно журнала команд. Содержимое окна рисунка 4 может отличаться от вашего, так как автор при написании викиучебника то и делал, что отвлекался.
Вы можете видеть записи последнего сеанса, которые отражают все введенные нами команды. Все журналы бережно сохраняются средой, чтобы вы могли вспомнить и восстановить команды, которые вводили ранее. Это может быть полезным, если вы забыли сохранить коды и завершили сеанс или, другой пример, если вы ввели очень длинную команду ранее, а теперь вам нужно ввести похожую, но лишь с небольшой разницей, или если сеанс был прерван из-за плохо отлаженного модуля, а команды вам ещё нужны.
Тем не менее, если вам не нужны журналы, вы всегда их можете удалить или очистить, воспользовавшись командами меню.
Математический пакет Scilab располагает широким и гибко настраиваемым аппаратом для построения двумерных графиков и трёхмерных изображений.
Математический пакет Scilab располагает широким и гибко настраиваемым аппаратом для построения двумерных графиков и трёхмерных изображений.
Перечислим основные функции для оформления графика:
xgrid() - добавление сетки на график;
xtitle("Название графика", "Название оси абсцисс", "Название оси ординат") - добавление подписей;
legend(. , .. ) - создание легенды с перечнем всех отображенных графиков в системе координат;
subplot(mnk) - функция разделения окна на матрицу, содержащую \( m \) строк, \(n столбцов\), а \(k \)- это номер ячейки, в которой будет отображен график.
Например, subplot(312) разобъёт графичекое окно на 3 строки, 1 столбец и нарисует график во второй ячейке:
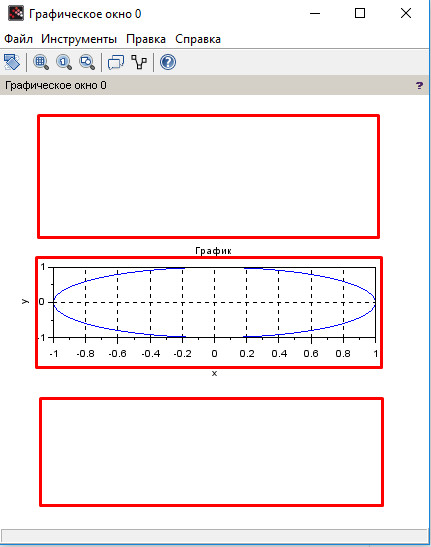
Расположение графика в графическом окне subplot(312).
Например, subplot(234) разобъёт графичекое окно на 2 строки, 3 столбца и нарисует график в четвёртой ячейке:
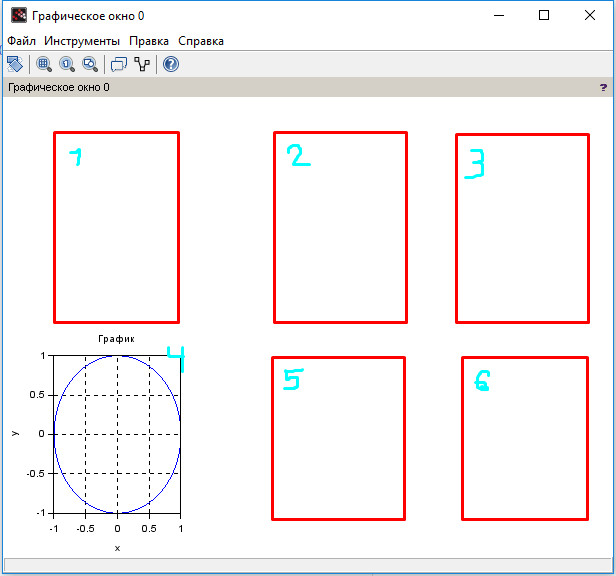
Расположение графика в графическом окне subplot(234).
5.1 Двумерные графики
Для построения графиков, в которых положение точки задаётся двумя величинами, в Scilab нужно воспользоваться функцией plot(x, y , s). Здесь первая переменная \( х \) - массив абсцисс, \( у \) - массив ординат, \( s \) - необязательный параметр, отвечающий за цвет графика, толщину и начертание линии.
Установить желаемый вид и цвет графика можно, указав строковый параметр \( s \), который может состоять из одного, двух или трёх символов, определяющие соответственно: цвет линии, тип маркера, тип линии графика. Возможные значения перечислены в таблицах 2-4.
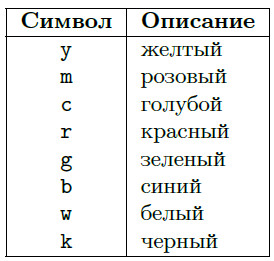
Таблица 2. Символы, определяющие цвет линии графика.

Таблица 3. Символы, определяющие тип линии графика.
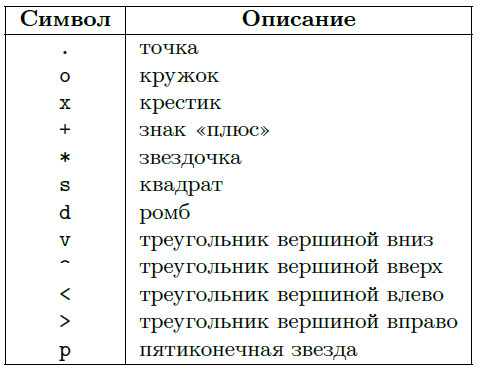
Таблица 4. Символы, определяющие тип маркера
Для демонстрации работы функции plot() построим графики траектории движения точки по заданным уравнениям \( x(t), y(t) \) на плоскости и в заданном диапазоне времени T (таблица 5). Определим внешний вид каждого из графиков, а также оформим систему координат со всеми необходимыми подписями (листинг 13). Результат работы программы представлен на рис. 7.
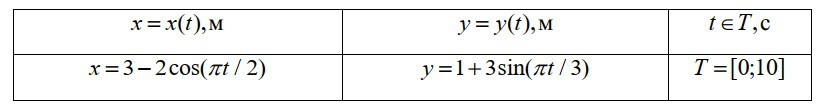
Таблица 5. Уравнения движения материальной точки и промежуток времени.
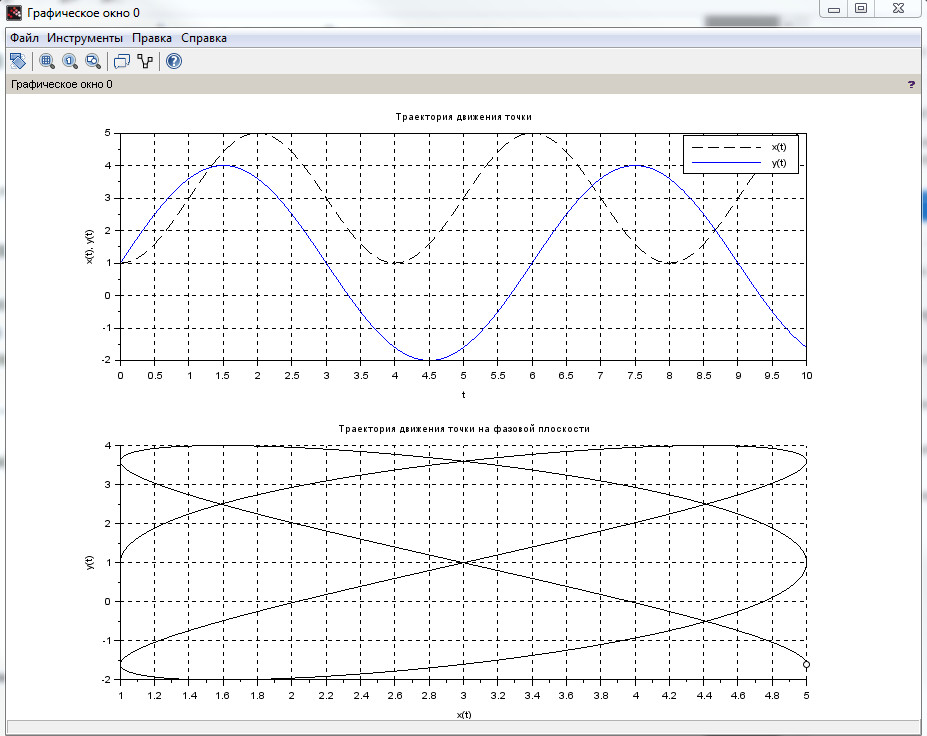
Рисунок 7. Построение графиков движения материальной точки.
Листинг 13. Программа построения графиков движения материальной точки.5.2 Построение трёхмерных изображений
Для построения поверхности в Scilab используются функции plot3d( plot3d1) и plot3d2(plot3d3). Их отличие состоит в том, что первая пара функций plot3d( plot3d1) строит поверхность из отдельно стоящих друг от друга грани (залитую одним цветом и залитую различными цветами соответсвенно), а вторая пара plot3d2(plot3d3) - цельное геометрическое тело.
Процесс построения графика функции вида \( Z(x,y) \) можно разделить на 3 этапа:
1. Создание прямоугольной сетки с помощью функции linspace();
2. Вычисление значений функции \( Z(x,y) \) в узлах сетки;
3. Вызов функции plot3d() или plot3d2().
В качестве примера, построим сферу в трехмерной системе координат с помощью функций plot3d1 и plot3d2.
Рисунок 8. Сфера, заданная параметрически, построенная с помощью функции plot3d1 (слева) и plot3d2 (справа).
Поверхность сферы в декартовых координатах \( (x,y,z) \) параметрически задаётся системой уравнений: \( f(n) = \begin x(u,v)=cos(u)cos(v) \\ y(u,v)=cos(u)sin(v) \\ z(u,v)=sin(u) \end \),
независимые переменные \( u и v \) изменяются на промежутке \( [-\pi; \pi] \). Результат работы программы представлен на рис.8, исходный код на листинге 14.
Обратите внимание, что при построении графиков поверхностей заданных параметрически , \(x(u,v), y(u,v) и z(u,v) \), необходимо сформировать матрицы \( X, Y и Z\) одинакового размера. Для этого массивы \( u и v \) должны иметь одинаковый размер.
Кроме того, если какая-либо функция из \( X, Y или Z\) зависит только от одного параметра \( u или v \), необходимо провести векторное умножение на единичный вектор ones() размерности, равной размерности параметра, от которого эта функция не зависит (см. строку 10 листинга 14).
Читайте также:




