Как сделать золотую спираль
Главный символ Вселенной, которому подчиняется и "Золотое сечение", и галактики, и водовороты, и расположение листьев и семян на многих растениях, и лихо закрученные раковины моллюсков, спиральные клубы дыма, спиральки сливок, растворяющихся в чашке кофе, музыка, поэзия, литература, архитектура и многое другое - логарифмическая спираль, математически выраженная в "Ряде Фибоначчи" (Леонардо Пизано Фибоначчи - итальянский математик XII - XIII веков), где каждое следующее число является суммой двух предыдущих: 1,1,2,3,5,8,13,21,34,55,89,144,233 и так далее. кстати Тора - священное писание евреев, тоже есть лишь большой цифровой код (каждая буква алфавита имеет числовое или цифровое выражение - своего рода система счисления - матрица. ), в котором зашифровано истинное имя Господа, состоящее по разным данным из 70 или 377 чисел и цифр (может быть и иное число - точной информацией не владею), кроме того считается, что ребёнок хранит этот код, находясь ещё в чреве матери, но теряет все воспоминания о нём, когда формируется его логос (программа к приходу во внешний мир), после чего только ведущим "правильный" образ жизни будет открыт проход в райские кущи. Ну, "избранный" народ - это разговор особый и очень философский. Именно этот вопрос, кстати, очень здорово освещён в одном из моих любимых фильмов Дэррена Аронофски - "Пи".
Таким образом имеем следующие логические соотношения между буквами (символами) и их числовым выражением.
Ну, например.
Символы bet и alep, поставленные вместе означают слово "отец", в числовом же выражении bet - это 2, а alep - это 1, итого имеем 2+1=3, то есть числовое выражение слова "отец" - это число, цифра 3.
Идём дальше - "мать" на иврите будет - tet (40) + alep (1) = 41 (числовое выражение слова "мать"). А теперь ещё интереснее - берём "отца" и "мать", то есть 3+41 и получаем 44, которые есть: 4 + 30 + 10 (посмотрите выше соответствующие символы), что равно (=) числу 44, которое обозначает "ребёнка" или "дитя", что вполне логично при сложении "отца" и "матери".
Если взять чуть поглубже, то имеем следующие результаты:
Как мы помним из Торы, символично-числовое выражение равное 144 обозначает "Райские кущи", ценность
"Древа познания" в которых равна такому же выражению, но только со значением числа 233. А теперь самое интересное: оба этих числа являются числами Фибоначчи и при делении 144 на 233 дают нам Тету (0,618. ) - математическое выражение того, как в Древней Греции (Элладе) обозначали пропорции "Золотой спирали."
Интересный факт о иврите:
Считается, что это не только универсальный цифровой код, но и весьма удобная система символов,
уложенная в "Звезду Давида", которая в свою очередь символизирует не только мужское и женское начало,
но и процесс проникновения духовного в материальное и многие другие тонкости мистического характера.
Геометрически это явление "Золотого сечения с золотой спиралью" было выражено ещё Пифагором, а затем уже в XIX веке широко популяризировано немецким философом и математиком Адольфом Цейзингом в его трактате, связанном с математической красотой, а главное - эстетикой в связке с "Золотым сечением".
На словах сечение выражается так: "Золотое сечение - это такое соотношение целого с его частью, которое полностью повторяет в пропорциях соотношение этой части целого в свою очередь с её собственной частью. И так деление может продолжаться до бесконечности. " Такой вид сечения или спирали присутствует во всём правильно развитом, что задумано природой. У уродства, так же есть свои законы искажений и искривлений, многие из которых обнаружили в относительно недавно открытых фракталах - описанных различными уравнениями кривых, так что и здесь всё предусмотрено.
На данный момент доказано, что такие процессы, как спад численности населения Карибских островов, периодичность эпидемий, появлений пятен на Солнце и многое другое - это тоже математически рассчитываемые процессы.
Относительной загадкой в наши дни остаётся только связь этой теории "Вселенского самоподобия" с чёткими научными очертаниями, которые уже довольно давно стала приобретать, к примеру, "Теория игр". И, конечно же, весьма интересен вопрос "Золотой закономерности" в том, что связано с фондовыми биржами и рынком акций, ведь это процесс достаточно хаотичный, но созданный человеком, следовательно, подверженный бионике, и возможно через это и удастся вывести единую теорию, которой подчиняются возрастания и спады всяческих процессов, как в природе, так и в технике, человеческой жизни, судьбе и многом другом, ведь законы кармы тоже очень логичны и выверены.
Главное иметь чистый, незамутнённый взгляд на всё это и не допускать мошеннических манипуляций, выдаваемых за экономические кризисы, "взлёты и падения", когда это просто выгодно крупному капиталу и так далее.
А пока - наслаждаемся картинками и раковинами, подписей к раковинам специально не делаю, сейчас они ни к чему.
"Золотые числа" Фибоначчи в геометрическом соотношении.
"Золотая спираль", вписанная в части целого, поделённого в "Золотой пропорции" : a/x = x/a-x.
"Золотая спираль" в растительном мире.
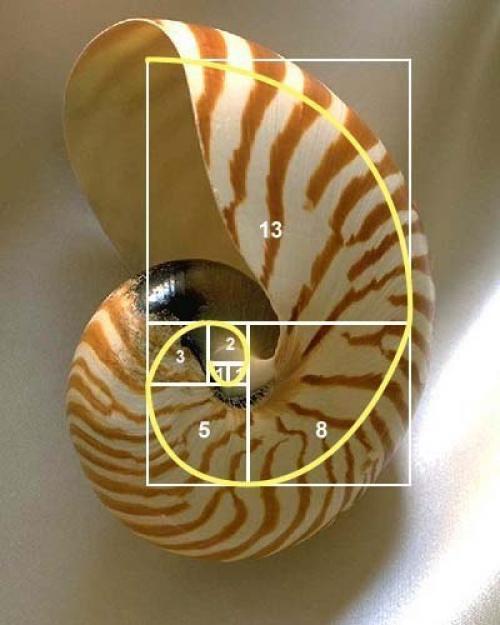
"Золотая спираль" раковины головоногого моллюска "Наутилус Помпилиус."
"Золотые пропорции" в линейном построении геометрических фигур: А - яблока и В - куриного яйца.
"Золотая спираль" галактики.
"Золотое сечение" в человеческом теле.
"Золотые пропорции" в черепах: А (слева) - антропоида - человекообразной обезьяны и В (справа) - человека.
"Золотое сечение" в памятниках античной скульптуры.
"Золотая пропорция" в фасаде типичного античного храмового сооружения.
"Золотые пропорции" храма Василия Блаженного в Москве.
"Золотые пропорции" в музыке.
"Золотые пропорции" соотношения построения строфы стиха Андрея Вознесенского "Гойя."
Разнообразные математические фрактальные кривые, описывающие множество природных форм, фигур, очертаний и линий.
Теперь переходим к изучению искусных завитков природы в виде раковин моллюсков:
является то, что по мере увеличения чисел ряда отношение двух соседних членов этого ряда асимптотически приближается к точной пропорции золотого сечения (1: 1, 618) основе красоты и гармонии в окружающей нас природе, в том числе и в человеческих отношениях.
Отметим, что сам Фибоначчи открыл свой знаменитый ряд, размышляя над задачей о количестве кроликов, которые в течение одного года должны родиться от одной пары.
У него получилось, что в каждом последующем месяце после второго число пар кроликов в точности следует цифровому ряду, которое ныне носит его имя. Поэтому не случайно, что и сам человек устроен по ряду Фибоначчи. Каждый орган устроен в соответствии с внутренней, или внешней двойственностью.
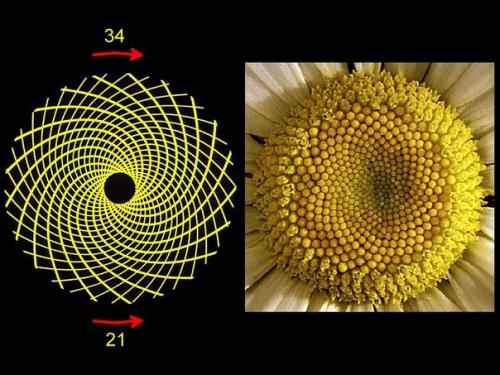
Следует сказать, что спираль Фибоначчи может быть двойной. Существуют многочисленные примеры этих двойных спиралей, встречающихся повсюду. Так спирали подсолнухов всегда соотносятся с рядом Фибоначчи.
Даже в обычной сосновой шишке можно увидеть эту двойную спираль Фибоначчи. Первая спираль идет в одну сторону, вторая - в другую. Таким образом, если посчитать число чешуек в спирали, вращающейся в одном направлении, и число чешуек в другой спирали, можно увидеть, что это всегда два последовательных числа ряда Фибоначчи.
Эти факты еще раз подтверждают, что закон о двойственности дает не только качественные, но и количественные результаты. Они заставляют задуматься о том, что окружающий нас макромир и микромир эволюционируют по одним и тем же законам - законам иерархии, и что эти законы едины для живой и для неживой материи. Other@sci.







Спираль Фибоначчи строят так:
В итоге получают красивую спираль, радиус которой постоянно и пропорционально увеличивается.
Так получается логарифмическая спираль, которая растет в соответствии с золотым сечением.
Числа Фибоначчи - числовая последовательность, где каждый последующий член ряда равен сумме двух предыдущих, то есть: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368. 75025. 3478759200, 5628750625. 260993908980000. 422297015649625. 19581068021641812000. Изучением сложных и удивительных свойств чисел ряда Фибоначчи занимались самые различные профессиональные ученые и любители математики.

В 1997 году несколько странных особенностей ряда описал исследователь Владимир Михайлов, который был убежден, что Природа (в том числе и Человек) развивается по законам, которые заложены в этой числовой последовательности.
Замечательным свойством числового ряда Фибоначчи является то, что по мере увеличения чисел ряда отношение двух соседних членов этого ряда асимптотически приближается к точной пропорции Золотого сечения (1:1,618) - основе красоты и гармонии в окружающей нас природе, в том числе и в человеческих отношениях.

Отметим, что сам Фибоначчи открыл свой знаменитый ряд, размышляя над задачей о количестве кроликов, которые в течении одного года должны родиться от одной пары. У него получилось, что в каждом последующем месяце после второго число пар кроликов в точности следует цифровому ряду, которое ныне носит его имя. Поэтому не случайно, что и сам человек устроен по ряду Фибоначчи. Каждый орган устроен в соответствии с внутренней, или внешней двойственностью.
Числа Фибоначчи привлекли математиков своей особенностью возникать в самых неожиданных местах. Замечено, например, что отношения чисел Фибоначчи, взятых через одно, соответствуют углу между соседними листьями на стебле растений, точнее, они говорят, какую долю оборота составляет этот угол: 1/2 - для вяза и липы, 1/3 - для бука, 2/5 - для дуба и яблони, 3/8 - для тополя и розы, 5/13 - для ивы и миндаля и т. д. Эти же числа вы найдете при подсчете семян в спиралях подсолнуха, в количестве лучей, отражающихся от двух зеркал, в количестве вариантов маршрутов переползания пчелы от одной соты к другой, во многих математических играх и фокусах.
В чем разница между спиралями золотого сечения и спиралью Фибоначчи? Спираль золотого сечения идеальна. Она соответствует Первоисточнику гармонии. Эта спираль не имеет ни начала, ни конца. Она бесконечна. Спираль Фибоначчи имеет начало, от которого она начинает “раскрутку”. Это очень важное свойство. Оно позволяет Природе после очередного замкнутого цикла осуществлять строительство новой спирали с “нуля”.

Следует сказать, что спираль Фибоначчи может быть двойной. Существуют многочисленные примеры этих двойных спиралей, встречающихся повсюду. Так, спирали подсолнухов всегда соотносятся с рядом Фибоначчи. Даже в обычной сосновой шишке можно увидеть эту двойную спираль Фибоначчи. Первая спираль идет в одну сторону, вторая - в другую. Если посчитать число чешуек в спирали, вращающейся в одном направлении, и число чешуек в другой спирали, можно увидеть, что это всегда два последовательных числа ряда Фибоначчи. Число этих спиралей 8 и 13. В подсолнухах встречаются пары спиралей: 13 и 21, 21 и 34, 34 и 55, 55 и 89. И отклонений от этих пар не бывает.

У Человека в наборе хромосом соматической клетки (их 23 пары) источником наследственных болезней являются 8, 13 и 21 пары хромосом.
Эти факты еще раз подтверждают, что закон о двойственности дает не только качественные, но и количественные результаты. Они заставляют задуматься о том, что окружающий нас Макромир и Микромир эволюцирует по одним и тем же законам - законам иерархии, и что эти законы едины для живой и для неживой материи.
Все это свидетельствует о том, что ряд чисел Фибоначчи представляет собой некий зашифрованный закон природы.
P.S. И помните, всего лишь изменяя свое сознание - мы вместе изменяем мир! © econet
Понравилась статья? Напишите свое мнение в комментариях.
Подпишитесь на наш ФБ:
Золотое сечение Фибоначчи. Божественная мера красоты

Ответ на этот вопрос сокрыт в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (род. ок. 1170 — умер после 1228), итальянский математик. Путешествуя по Востоку, познакомился с достижениями арабской математики; способствовал передаче их на Запад.
После его открытия числа эти так и стали называться именем известного математика. Удивительная суть последовательности чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.
Итак, числа, образующие последовательность:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то пpевосходящая, то не достигающая его. (Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично)
Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряда… Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)
Итак, Золотая пропорция = 1 : 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
Тело человека и золотое сечение
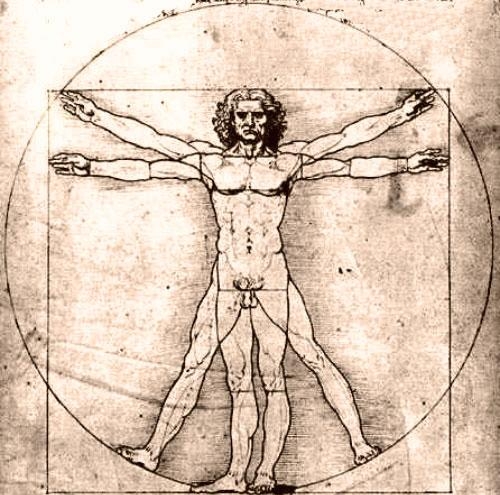
Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону Золотой пропорции.
Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы:
Первый пример золотого сечения в строении тела человека:
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.
Кроме этого есть и еще несколько основных золотых пропорции нашего тела:
* расстояние от кончиков пальцев до запястья до локтя равно 1:1.618;
* расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618;
* расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618;
* расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618;
* расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618;
* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;
* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618:

Золотое сечение в чертах лица человека как критерий совершенной красоты.
В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.
К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.
На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:
* Высота лица / ширина лица;
* Центральная точка соединения губ до основания носа / длина носа;
* Высота лица / расстояние от кончика подбородка до центральной точки соединения губ;
* Ширина рта / ширина носа;
* Ширина носа / расстояние между ноздрями;
* Расстояние между зрачками / расстояние между бровями.
Рука человека
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.
* Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца);
* Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения;
* У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи:
Золотая пропорция в строении легких человека
Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.
Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.
* Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.
Строение золотого ортогонального четырехугольника и спирали
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
В геометрии прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.
Золотой прямоугольник также обладает многими удивительными свойствами. Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).
Полюс спирали лежит на пересечении диагоналей начального прямоугольника и первого отрезаемого вертикального. Причем, диагонали всех последующих уменьшающихся золотых прямоугольников лежат на этих диагоналях. Разумеется, есть и золотой треугольник.
Английский дизайнер и эстетик Уильям Чарлтон констатировал, что люди считают спиралевидные формы приятными на вид и используют их вот уже тысячелетия, объяснив это так:
В природе
* Лежащее в основе строения спирали правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях. Самые наглядные примеры — спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестков роз и т.д.;

* Ботаники установили, что в расположении листьев на ветке, семян подсолнечника или шишек сосны со всей очевидность проявляется ряд Фибоначчи, а стало быть, проявляется закон золотого сечения;
Всевышний Господь каждому Своему творению установил особую меру и придал соразмерность, что подтверждается на примерах, встречающихся в природе. Можно привести великое множество примеров, когда процесс роста живых организмов происходит в строгом соответствии с формой логарифмической спирали.
Все пружинки в спирали имеют одинаковую форму. Математики установили, что даже при увеличении размеров пружинок форма спирали остается неизменной. В математике нет более иной формы, которая обладала бы такими же уникальными свойствами как спираль.
Строение морских раковин
Ученые, изучавшие внутреннее и внешнее строение раковин мягкотелых моллюсков, обитающих на дне морей, констатировали:

У большинства улиток, которые обладают раковинами, раковина растет в форме логарифмической спирали. Однако нет сомнения, что эти неразумные существа не имеют представления не только о логарифмической спирали, но не обладают даже простейшими математическими знаниями, чтобы самим создать себе спиралевидную раковину.
Но тогда как же эти неразумные существа смогли определить и избрать для себя идеальную форму роста и существования в виде спиральной раковины? Могли ли эти живые существа, которых ученых мир называет примитивными формами жизни, рассчитать, что идеальной для их существования будет логарифмическая форму ракушки?
Конечно же нет, потому что такой замысел невозможно осуществить без наличия разума и знаний. Но таковым разумом не обладают ни примитивные моллюски, ни бессознательная природа, которую, правда, некоторые ученые называют создательницей жизни на земле(?!)
Пытаться объяснить происхождение подобной даже самой примитивной формы жизни случайным стечением неких природных обстоятельств по меньшей мере абсурдно. Совершенно ясно, что этот проект является осознанным творением.
Сэр Томпсон делает такой комментарий:
Наутилус, размером в несколько сантиметров в диаметре, представляет собой самый выразительный пример гномового вида роста. С.Моррисон так описывает этот процесс роста наутилуса, спланировать который даже человеческим разумом представляется довольно сложным:
Приведем лишь некоторые типы спиралевидных раковин имеющих логарифмическую форму роста в соответствии с их научными названиями:
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.
Все обнаруженные ископаемые останки раковин также имели развитую спиральную форму.
Однако логарифмическая форма роста встречается в животном мире не только у моллюсков. Рога антилоп, диких козлов, баранов и прочих подобных животных также развиваются в виде спирали по законам золотой пропорции.
Золотое сечение в ухе человека
Рога и бивни животных, развивающиеся в форме спирали
Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль. Пауки всегда плетут свои паутины в виде логарифмической спирали. Строение таких микроорганизмов, как планктоны ( виды globigerinae, planorbis, vortex, terebra, turitellae и trochida) также имеют форму спирали.
Золотое сечение в строении микромиров
Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.
В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.
Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.
Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:
Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.
Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.
В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.
Золотые пропорции в строении молекулы ДНК

Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).
21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618
Золотое сечение в строении снежинок
Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору.
Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.
Золотые пропорции в космическом пространстве

Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.
Золотое сечение в физике
Последовательность чисел Фибоначчи и формула золотого сечения непосредственным образом затрагивает и сферу физики и физических законов:
Строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле. Это является самым ярким доказательством их осознанной сотворенности согласно некоему проекту, замыслу. Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.
Читайте также:


