Как сделать золотой треугольник
Фотографии с правильно выбранной композицией заставляют задержать на них взгляд и рассмотреть детали. Они рассказывают историю, создают настроение и заставляют задуматься.
Золотое сечение в фотографии - основной и мощный инструмент для получения динамичных, интересных снимков. Правило золотого сечения встречается и в природе, причем повсеместно. О нем знали еще в древнем Египте. Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. Этот феномен изучил и стал применять на практике известный ученый, художник и скульптор Леонардо Да Винчи.
Для желающих узнать больше - видео:
Мы затронем только практическую часть применения золотого сечения в фотографии. Кадр условно делиться на три части по горизонтали и вертикали:

- Если расположитьлинию горизонта по одной из горизонтальных линий, то кадр будет смотреться гармоничней. Но на какой из линий, на верхней или нижней?
- Если вы хотите сконцентрировать внимание зрителя на земле или воде – то лучше на верхней.
- Если же вы делаете акцент на интересном, выразительном небе – то на нижней.
- Если вы снимаете портрет, то лучше размещать глаза на верхней горизонтальной линии.
- Если вы снимаете человека в полный рост, то лучше размещать его на правой или левойвертикальной линии.
- Очень важно следить за тем, в какую сторону направляется человек, или куда направлен его взгляд. Например, если человек смотрит влево, то его соответственно необходимо разместить на правой горизонтальной линии, что бы перед ним оставалось пространство.
В современных фотоаппаратах уже есть функция-подсказка, которая отображает линии правила третей на мониторе или в видоискателе.

Размещайте важные части композиции вдоль линий, а самое главное — на их пересечении.
Золотое сечение может прослеживаться не только в прямоугольной сетке, но и в диагоналях или спирали. Принцип расположения предметов – тот же, по основным линиям и в точках их пересечений.


Фото: Steve McCurry

Фото: Joe McNally

Фото: Richard Barnabe
ДИАГОНАЛЬНОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Применяя правило золотого сечения проводим диагонали и получаем прямоугольник состоящий из трех секторов. Этот прямоугольник можно поворачивать как угодно Если скомпонуете свой кадр так, чтобы три разных объекта примерно располагались в этих секторах, а главные объекты в более крупных секциях - то композиция будет выглядеть очень гармонично.

Это правило используется, если у вас в кадре есть несколько областей, различающихся по смыслу.

СПИРАЛЬНОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Используя эту спираль при построении композиции в кадре (ее можно перевернуть вверх ногами или в другую сторону), мы получим кадр с четко выраженным предметом в центре спирали.
Золотое сечение Фибоначчи. Божественная мера красоты

Ответ на этот вопрос сокрыт в удивительных числах, которые были открыты итальянским математиком средневековья Леонардо Пизанским, более известным по именем Фибоначчи (род. ок. 1170 — умер после 1228), итальянский математик. Путешествуя по Востоку, познакомился с достижениями арабской математики; способствовал передаче их на Запад.
После его открытия числа эти так и стали называться именем известного математика. Удивительная суть последовательности чисел Фибоначчи состоит в том, что каждое число в этой последовательности получается из суммы двух предыдущих чисел.
Итак, числа, образующие последовательность:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …
В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875… и через раз то пpевосходящая, то не достигающая его. (Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично)
Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряда… Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)
Итак, Золотая пропорция = 1 : 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
Тело человека и золотое сечение
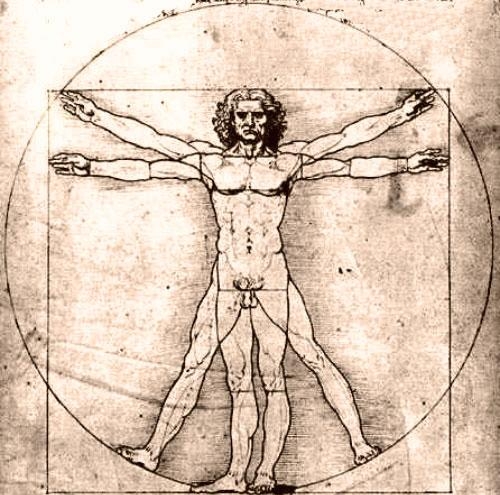
Художники, ученые, модельеры, дизайнеры делают свои расчеты, чертежи или наброски, исходя из соотношения золотого сечения. Они используют мерки с тела человека, сотворенного также по принципу золотой сечения. Леонардо Да Винчи и Ле Корбюзье перед тем как создавать свои шедевры брали параметры человеческого тела, созданного по закону Золотой пропорции.
Пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению. Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенными. Принцип расчета золотой меры на теле человека можно изобразить в виде схемы:
Первый пример золотого сечения в строении тела человека:
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618.
Кроме этого есть и еще несколько основных золотых пропорции нашего тела:
* расстояние от кончиков пальцев до запястья до локтя равно 1:1.618;
* расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618;
* расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1.618;
* расстояние точки пупа до коленей и от коленей до ступней равно 1:1.618;
* расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1.618;
* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618;
* расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки равно 1:1.618:

Золотое сечение в чертах лица человека как критерий совершенной красоты.
В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения. Однако не бросайтесь тотчас же за линейкой, чтобы обмерять лица всех людей. Потому что точные соответствия золотому сечению, по мнению ученых и людей искусства, художников и скульпторов, существуют только у людей с совершенной красотой. Собственно точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.
К примеру, если мы суммируем ширину двух передних верхних зубов и разделим эту сумму на высоту зубов, то, получив при этом число золотого сечения, можно утверждать, что строение этих зубов идеально.
На человеческом лице существуют и иные воплощения правила золотого сечения. Приведем несколько таких соотношений:
* Высота лица / ширина лица;
* Центральная точка соединения губ до основания носа / длина носа;
* Высота лица / расстояние от кончика подбородка до центральной точки соединения губ;
* Ширина рта / ширина носа;
* Ширина носа / расстояние между ноздрями;
* Расстояние между зрачками / расстояние между бровями.
Рука человека
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.
* Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца);
* Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения;
* У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи:
Золотая пропорция в строении легких человека
Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.
Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче.
* Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.
Строение золотого ортогонального четырехугольника и спирали
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
В геометрии прямоугольник с таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.
Золотой прямоугольник также обладает многими удивительными свойствами. Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).
Полюс спирали лежит на пересечении диагоналей начального прямоугольника и первого отрезаемого вертикального. Причем, диагонали всех последующих уменьшающихся золотых прямоугольников лежат на этих диагоналях. Разумеется, есть и золотой треугольник.
Английский дизайнер и эстетик Уильям Чарлтон констатировал, что люди считают спиралевидные формы приятными на вид и используют их вот уже тысячелетия, объяснив это так:
В природе
* Лежащее в основе строения спирали правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях. Самые наглядные примеры — спиралевидную форму можно увидеть и в расположении семян подсолнечника, и в шишках сосны, в ананасах, кактусах, строении лепестков роз и т.д.;

* Ботаники установили, что в расположении листьев на ветке, семян подсолнечника или шишек сосны со всей очевидность проявляется ряд Фибоначчи, а стало быть, проявляется закон золотого сечения;
Всевышний Господь каждому Своему творению установил особую меру и придал соразмерность, что подтверждается на примерах, встречающихся в природе. Можно привести великое множество примеров, когда процесс роста живых организмов происходит в строгом соответствии с формой логарифмической спирали.
Все пружинки в спирали имеют одинаковую форму. Математики установили, что даже при увеличении размеров пружинок форма спирали остается неизменной. В математике нет более иной формы, которая обладала бы такими же уникальными свойствами как спираль.
Строение морских раковин
Ученые, изучавшие внутреннее и внешнее строение раковин мягкотелых моллюсков, обитающих на дне морей, констатировали:

У большинства улиток, которые обладают раковинами, раковина растет в форме логарифмической спирали. Однако нет сомнения, что эти неразумные существа не имеют представления не только о логарифмической спирали, но не обладают даже простейшими математическими знаниями, чтобы самим создать себе спиралевидную раковину.
Но тогда как же эти неразумные существа смогли определить и избрать для себя идеальную форму роста и существования в виде спиральной раковины? Могли ли эти живые существа, которых ученых мир называет примитивными формами жизни, рассчитать, что идеальной для их существования будет логарифмическая форму ракушки?
Конечно же нет, потому что такой замысел невозможно осуществить без наличия разума и знаний. Но таковым разумом не обладают ни примитивные моллюски, ни бессознательная природа, которую, правда, некоторые ученые называют создательницей жизни на земле(?!)
Пытаться объяснить происхождение подобной даже самой примитивной формы жизни случайным стечением неких природных обстоятельств по меньшей мере абсурдно. Совершенно ясно, что этот проект является осознанным творением.
Сэр Томпсон делает такой комментарий:
Наутилус, размером в несколько сантиметров в диаметре, представляет собой самый выразительный пример гномового вида роста. С.Моррисон так описывает этот процесс роста наутилуса, спланировать который даже человеческим разумом представляется довольно сложным:
Приведем лишь некоторые типы спиралевидных раковин имеющих логарифмическую форму роста в соответствии с их научными названиями:
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.
Все обнаруженные ископаемые останки раковин также имели развитую спиральную форму.
Однако логарифмическая форма роста встречается в животном мире не только у моллюсков. Рога антилоп, диких козлов, баранов и прочих подобных животных также развиваются в виде спирали по законам золотой пропорции.
Золотое сечение в ухе человека
Рога и бивни животных, развивающиеся в форме спирали
Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль. Пауки всегда плетут свои паутины в виде логарифмической спирали. Строение таких микроорганизмов, как планктоны ( виды globigerinae, planorbis, vortex, terebra, turitellae и trochida) также имеют форму спирали.
Золотое сечение в строении микромиров
Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.
В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.
Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.
Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:
Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.
Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.
В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.
Золотые пропорции в строении молекулы ДНК

Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра).
21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618
Золотое сечение в строении снежинок
Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору.
Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.
Золотые пропорции в космическом пространстве

Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.
Золотое сечение в физике
Последовательность чисел Фибоначчи и формула золотого сечения непосредственным образом затрагивает и сферу физики и физических законов:
Строение всех встречающихся в природе живых организмов и неживых объектов, не имеющих никакой связи и подобия между собой, спланировано по определенной математической формуле. Это является самым ярким доказательством их осознанной сотворенности согласно некоему проекту, замыслу. Формула золотого сечения и золотые пропорции очень хорошо известны всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.
В фотографии существует довольно много правил композиции. Вы, вероятно, слышали о таких вещах, как ведущие линии, золотое сечение и Правило третей. В сегодняшней статье вы узнаете, как применить правило Золотого треугольника к своей работе.
Скалистая морская сцена с наложением правила третей

Эта фотография использует правило третей, но есть также диагонали, которые проходят через рамку, образованную линиями, которые делают камни.
Городской горизонт с наложением правила третей

Правило третей является классическим по своей композиции. Эта фотография показывает, насколько сильным может быть этот тип композиции.
Вы не сильно ошибетесь, если будете придерживаться главной темы, имея простой фон, состоящий из правила третей. Но через некоторое время эта формула может немного надоесть и встанет вопрос, как можно это изменить? Один из подходов состоит в том, чтобы рассмотреть вариант правила третей, и это золотой треугольник.
При таком типе композиции вы теперь будете использовать диагонали на своей фотографии. Это придаст вашей фотографии более динамичный вид.
Как формируется композиция Золотого Треугольника?
Теперь вы будете использовать треугольники вместо коробок. Это создаст диагонали по всей вашей композиции.
Представьте себе ваш кадр и нарисуйте диагональную линию от верхнего левого угла, а затем проведите ее вниз до нижнего правого угла. Впрочем, не имеет значения, какие углы, главное — вам нужна диагональная линия поперек вашего кадра.
Теперь от нижнего левого угла проведите линию до диагональной линии, которая пересекает ее под прямым углом. Вы можете завершить эту линию до края вашего кадра, если хотите. Проделайте то же самое с линией из верхнего правого угла, которая также пересекает исходную линию под прямым углом.
Теперь у вас будут треугольники, которые образуют фотографическую композицию, известную как Золотой треугольник. Эта композиция также может быть сформирована с помощью вертикального или горизонтального прямоугольника.
Изображение здания с солнечным сиянием через арку и композиционное наложение

На этой фотографии интерес представляет солнечный луч, проходящий через фасад здания. Он сидит на одной из пересекающихся линий.
Как вы можете составить фотографию для Золотого Треугольника?
Как только вы настроите сетку для композиции Золотого треугольника, вы заметите две точки пересечения.
Один слева, а другой справа от вашей композиции. Как и в случае с правилом третей, вы стремитесь поставить свою точку интереса над этой точкой пересечения.
Фотографии, как правило, имеют точку интереса и ведущие линии, которые проходят через них. Вот как они должны быть обработаны для золотого треугольника.
Черно-белое изображение лодок в воде с наложением композиции

Интересный способ выстраивания лодок на этой фотографии создает сильную композицию с некоторыми красивыми треугольными образованиями.
Какие темы лучше всего подходят для этой композиции? Есть места, где композиция Золотого треугольника возможна только с голландскими углами. Голландские ракурсы — это не все представления о хорошей фотографии.
Итак, какой вид композиции будет работать для этого типа фотографий? Ниже приведены несколько идей для вас, хотя, как и в любом виде искусства, в конце концов, вам придется использовать свое собственное суждение.
Портреты — стандартный портрет, вероятно, здесь не сработает. У тебя будет слишком много прямых линий. Вместо этого посмотрите на портреты, где модель сидит или лежит. Вы можете играть с углами, чтобы создать диагонали. Вы также должны стремиться использовать руки и ноги для создания диагоналей, которые образуют золотые треугольники.
Горы — когда линия горизонта не плоская, у вас есть больше возможностей для формирования композиции Золотого треугольника. Используйте диагональную линию горизонта, которая ведет к вашему основному объекту. Вам не нужно использовать горы, вы можете использовать песчаную дюну во многом таким же образом.
Дорога – вы можете использовать дорогу, которая проходит через ваш кадр по диагонали, чтобы создать композицию Золотого треугольника. Встать на обочине дороги — это один из способов заставить дорогу проходить через кадр по диагонали. Если вы можете подняться над дорогой и убрать линию горизонта, это также может помочь с композицией.

Изображение человека через дверной проем с композиционным наложением
Общие вопросы о фотографической композиции.
Что подразумевается под Золотым треугольником?
Золотой треугольник — это правило композиции
Это правило чем-то напоминает правило третей. Однако то, как делится фотография, немного отличается.
Вместо прямых линий в качестве направляющей композиции выступает ряд диагональных линий, образующих прямоугольные треугольники. Основной предмет фотографии должен сидеть на пересечении этих треугольников.
Каковы 7 элементов фотографии?
Эти 7 элементов относятся к основным компонентам хорошей фотографии, которые вы можете назвать элементами дизайна.
Это — цвет, форма, линии, вид, текстура, пространство и контраст. Каждая фотография, которую вы сделаете, будет использовать некоторые или даже все эти элементы для создания привлекательного образа.
Как используется Золотое сечение в фотографии?
Золотое сечение — это альтернативный способ составления фотографии. Он основан на прямоугольниках внутри прямоугольников, которые уменьшаются в размерах с помощью композиции.
Когда вы применяете это правило в фотографии, разделы фотографии выстраиваются в линию. По мере того, как вы все больше смотрите на предмет фотографии, компоненты продолжают выстраиваться в соответствии с этим золотым сечением.
Вывод
Получение сильной композиции — это ключ к хорошей фотографии. Очень важно попробовать разные способы обрамления фотографии.
Сначала будет трудно найти нужную композицию, поэтому чем больше вы будете практиковаться, тем легче будет. Это немного похоже на изучение нового языка, только это визуальный язык. С практикой новый тип композиции станет частью вашего подсознания.
Как и во всем в жизни, хорошо пробовать что-то новое и расширять свой кругозор. Это путь к улучшению вашей работы. Так что попробуйте Золотой треугольник и посмотрите, куда он приведет вашу фотографию.

Посмотрите работу "Гармония". Аэрография выполнена по мотивам работ Леонардо да Винчи.
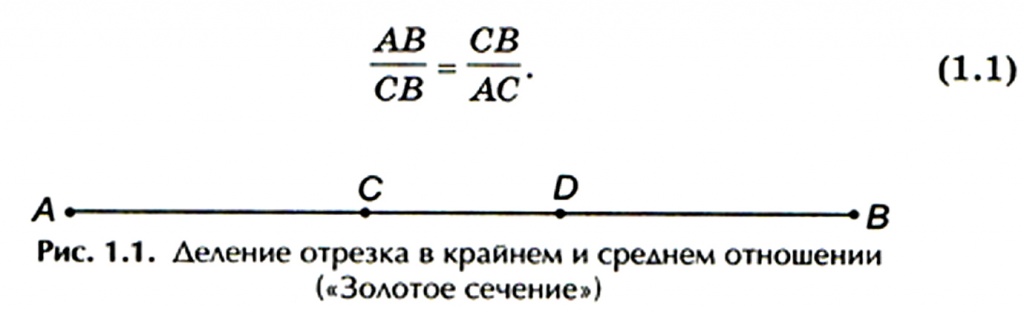
Обозначим пропорцию (1.1) через х. Тогда, учитывая, что АВ = АС + СВ, пропорцию (1.1) можно записать в следующем виде:
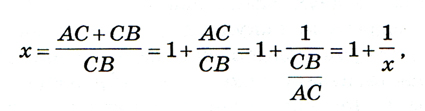
откуда вытекает следующее алгебраическое уравнение для вычисления искомой пропорции х:
х* = х + 1. (1.2)
x* - в квадрате
Приближенное значение золотой пропорции равно:
= 1,61803 39887 49894 84820 45868 34365 63811 77203…
ЗОЛОТЫЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ
На основе вышеизложенных пропорций в геометрии определены такие понятия золотых геометрических фигур:
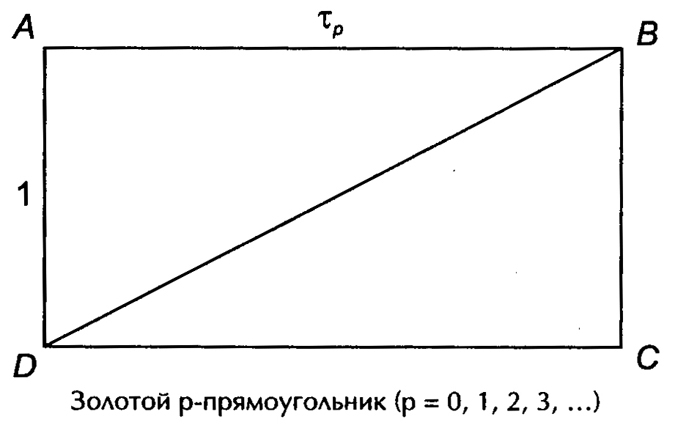
- золотой прямоугольник (в котором отношение большей стороны к меньшей равно золотой пропорции);
- золотой прямоугольный треугольник;
- золотой эллипс;
- золотой равнобедренный треугольник.
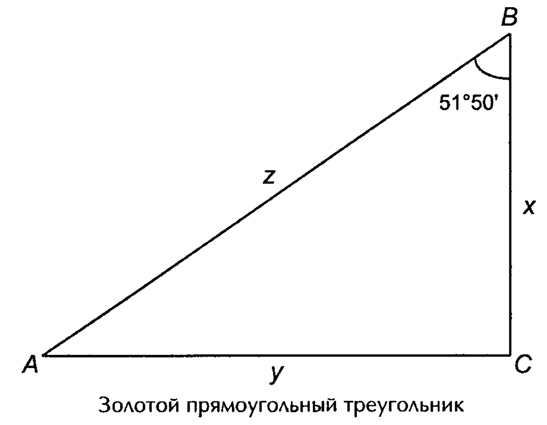
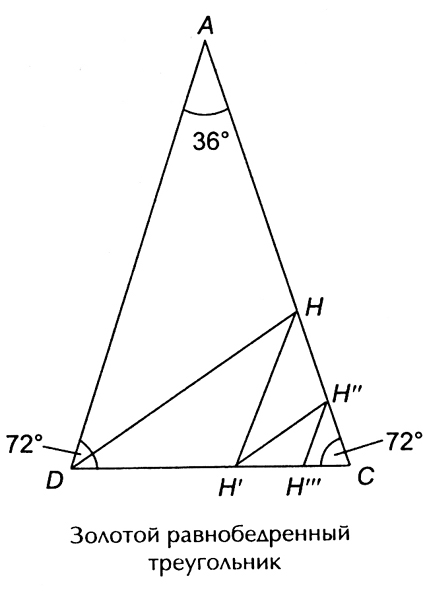
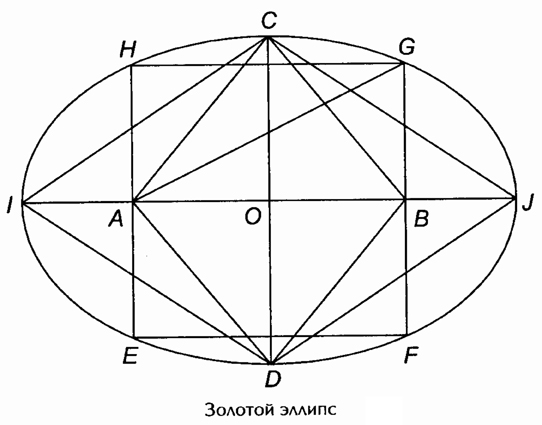
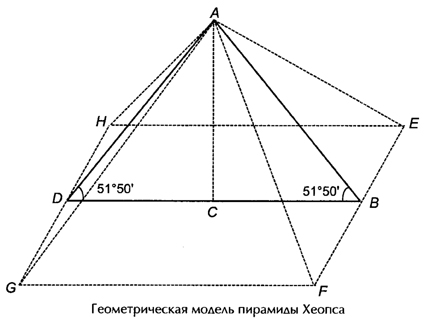
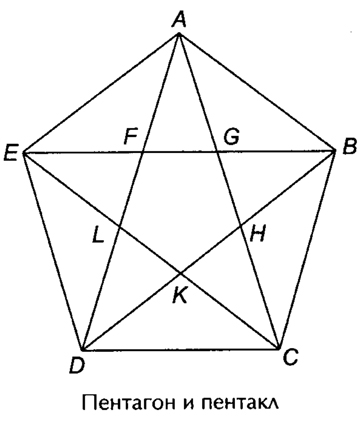

Пентагон и пентакл включают в себя ряд замечательных фигур, которые широко использовались в произведениях искусства. В античном искусстве широко известен так называемый закон золотой чаши, которые использовали античные скульпторы и золотых дел мастера. Заштрихованная часть пентагона дает схематическое представление золотой чаши.
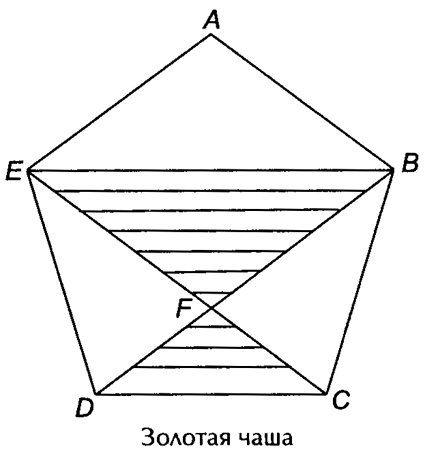
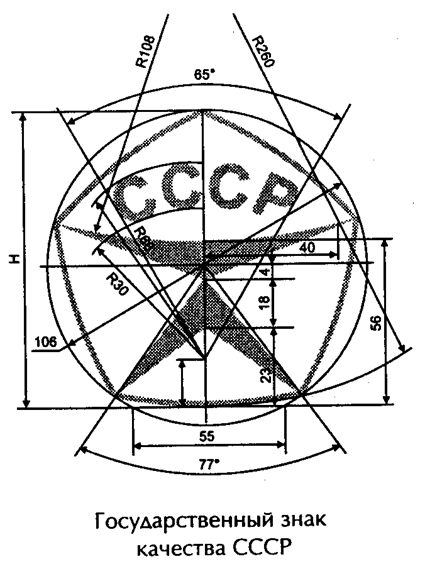
Когда-то в Советском Союзе существовал Государственный знак качества, в котором явно просматриваются мотивы золотой чаши.
В живой природе широко распространены формы, основанные на пентагональной симметрии – морские звезды, морские ежи, цветы..

ГАРМОНИЯ ЗОЛОТОГО СЕЧЕНИЯ
(краткий обзор истории искусства)
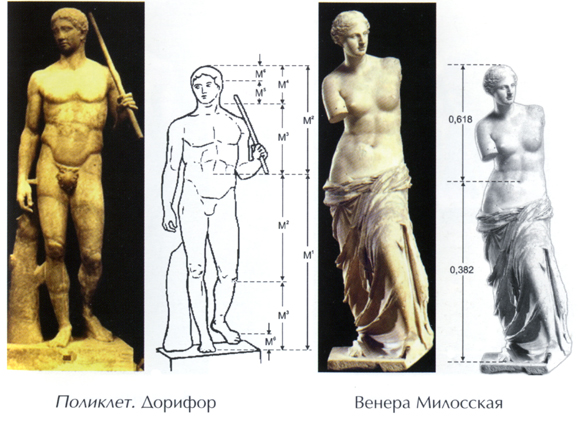
Эталоном красоты человеческого тела, образцом гармонического телосложения издав-на и по праву считаются великие творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. В своих творениях греческие мастера использовали принцип золотой пропорции. Одним из высших достижений классического греческого искусства может служить статуя Дорифора, изваянная Поликтетом в V веке до н. э. Эта статуя считается наилучшим примером для анализа пропорций идеального человеческого тела, установленных античными греческими скульпторами, и напрямую связана с Золотым сечение. М=0,618…
Венера Милосская, статуя богини Афродиты и эталон женской красоты, является од-ним из лучших памятников греческого скульптурного искусства.



Пропорции статуи Давида (работы Микеланджело) основаны на Золотом сечении.

Яркий пример архитектуры барокко, Смольный собор в Санкт-Петербурге, производит неизгладимое впечатление. В его основных пропорциях так же усматривается Золотое сечение.



Строительство штаб-квартиры ООН в Нью-Йорке было завершено в 1943 году. Здание привлекло тогда всеобщее внимание не только как общественное сооружение, созданное с применением новейших архитектурных средств, но и как первый пример использования сплошного солнцемодулирущего экрана на одном из фасадов. В этом здании также просматриваются мотивы Золотого сечения. В композиции здания четко выделяются три поставленных друг на друга золотых прямоугольника, которые и являются его главной архитектурной идеей.

В течение многих тысячелетий Золотое сечение было объектом восхищения и поклонения выдающихся ученых и мыслителей: Пифагора, Платона, Евклида, Луки Пачоли, Иоганна Кеплера, Павла Флоренского…
В настоящее время Золотое сечение оказывается источником новых плодотворных идей в математике и теоретической физике, биологии и ботанике, экономике и компьютерной науке…
Читайте также:


