Как сделать удельный вес в экселе
По роду своей деятельности большинство специалистов, задействованных в области инженерных изысканий, и инженеры-геологи в частности, сталкиваются с большим количеством данных. Такие данные для удобства иногда располагаются в таблицах, которые можно наблюдать, к примеру, в нормативной документации. Но порой массива данных бывает недостаточно для получения необходимых значений и здесь на помощь в некоторых случаях может прийти такой математический инструмент, как интерполяция.
Поэтому возникла идея подготовки и публикации данного материала. В нем рассмотрена одна из возможностей использования программы Excel для нахождения промежуточных значений, которая входит в стандартный пакет MS Office, установленный в большинстве компаний.
Вы научитесь делать это самостоятельно, создадите свой файл с расчетами, оцените все его преимущества и сведете к минимуму так называемый человеческий фактор. Сам материал изложен общедоступным языком, а формулы упрощены для лучшего их понимания.
Все примеры приводятся в русскоязычной версии MS Office Excel 2013, однако и в более ранних большинство формул должно работать, возможно, за исключением тех, в которых будет задано большое количество условий.
Введение
Интерполяция – в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. И в университете, на парах математики вы с ней скорее всего знакомились.
Вариантов интерполяции существует некоторое множество, но мы будем рассматривать именно линейную интерполяцию, которую в Excel можно выполнять с помощью функции ПРЕДСКАЗ. Стоит отметить, что сама эта функция имеет более широкие возможности.
Сначала мы будем использовать не все данные из этой таблицы, а только часть. Например – значения moed для супесей при коэффициенте пористости e 0,65-0,75. Создайте такую же таблицу в Excel. Обратите внимание, что содержимое должно соответствовать тем же строкам и столбцам, что и в примере.
На оси X в данном случае будут располагаться значения коэффициента пористости e , а на оси Y – коэффициента moed , соответственно. Посаженные по координатам точки будут соединены отрезком, который мы условно обозначим ab (рис.1).

Давайте представим, что нам необходимо найти moed для супеси с коэффициентом пористости 0,7. Для этого от числа 0,7 на оси X мы проведем параллельную оси Y линию fc до нашего отрезка. Затем от точки пересечения проведем к оси Y уже параллельно оси X линию cd . И получим значение moed – 2,3 графику (рис. 2).

Это графический способ. Математически формула линейной интерполяции в данном случае выглядит так:
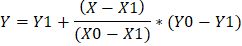
где Y0=2,1; Y1=2,5; X=0,7; X0=0,75; X1=0,65
На рисунке 3 приведена диаграмма с соответствующими обозначениями.

Подставив все эти значения в формулу, получаем:
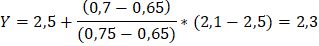
Y – есть наше искомое значение moed для коэффициента пористости 0,70, которое для супеси равно 2,3.
Удобен ли такой расчет на листе бумаги? Не очень, т.к. отнимает много времени. Однако уже хорошо, что он вообще выполняется.
На данный момент, когда уже понятно, как выглядит линейная интерполяция графически и как она рассчитывается математически, для упрощения используем функцию ПРЕДСКАЗ, которая может сделать то же самое для двух наших значений e и соответствующих им moed .
Сама функция в Excel имеет следующий вид:
ПРЕДСКАЗ(x;известные_значения_y;известные_значения_x)
Возвращаемся к нашему примеру и в ячейку M5 запишем известное значение коэффициента пористости – 0,70, а в ячейку N5 впишем следующую формулу:
=ПРЕДСКАЗ(M5;M3:N3;M2:N2)
Нажмем Enter. В результате в ячейке N5 получим значение 2,3, которое соответствует нашему искомому коэффициенту moed . Изменяя значение в ячейке M5 от 0,65 до 0,75, вы будете получать в соответствии с ним новые значения в ячейке N5 (рис. 4).

Теперь полностью автоматизируем расчеты и разберем на примерах различные варианты. Для каждого из них создадим отдельный лист в книге Excel.
Важно! Все значения должны быть размещены в тех же строках и столбцах, что и в примерах.
Пример 1. Получение коэффициента moed

Так как зависимость значений в таблице не линейная и это наглядно видно, если построить по ним все ту же диаграмму и выполнить линейную аппроксимацию (рис. 6, 7, 8), мы не можем взять сразу весь массив данных.

Рис. 6. Точечная диаграмма и линейная аппроксимация по значениям из таблицы 5.1, СП 22.13330.2016 для супесей

Рис. 7. Точечная диаграмма и линейная аппроксимация по значениям из таблицы 5.1, СП 22.13330.2016 для суглинков

Рис. 8. Точечная диаграмма и линейная аппроксимация по значениям из таблицы 5.1, СП 22.13330.2016 для глин
Поэтому сначала выберем по два значения, внутри диапазона которых будет проведена интерполяция. А затем сделаем это для всех данных из таблицы по очереди.
Далее будет указано, в какую ячейку, какое содержимое вписывать. Формат ячеек может быть, как общий, так и числовой.

Затем для большего удобства сделаем выбор типа грунта из выпадающего списка. Для этого:
Выберите ячейку B2
Остается только получить нужный результат. Впишите формулу в ячейку B6:
Если вы все сделали правильно, то ваш лист Excel должен иметь следующий вид (рис. 11):

Стоит отметить, что добиться подобного можно и другими способами. Например, используя связку функций Excel: ГПР, ИНДЕКС и ПОИСКПОЗ. При этом не потребуется интерполировать всю таблицу, а условных операторов будет меньше. Рассмотрим этот вариант ниже.
Пример 2. Получение расчетного сопротивления глинистых непросадочных грунтов

Далее будет указано, в какую ячейку, какое содержимое вписывать. Формат ячеек может быть как общий, так и числовой.

Остается только получить R0 . Для этого впишите такую формулу в ячейку B5 :
В результате лист Excel должен иметь следующий вид (рис. 13).

Как можно заметить, в этом примере для того чтобы не выполнять поочередную интерполяцию всех значений таблицы, были использованы функции ВПР, ИНДЕКС и ПОИСКПОЗ, что значительно упростило задачу. Изменяя тип грунта, а так же значения в ячейках B3 и B4 , вы неизменно получите значение расчетного сопротивления в ячейке B5 .
Пример 3. Косвенный метод определения плотности p песков по результатам статического зондирования
В качестве альтернативы лабораторному методу определения плотности природного сложения аллювиальных и флювиогляциальных песков, залегающих на глубине до 6 м, Л.Г. Мариупольским была предложена возможность определения p с помощью результатов статического зондирования, природной влажности ( W ) и плотности частиц грунта ( ps ). Сопоставив 171 определение коэффициента пористости е , полученного в лабораторных условиях из ненарушенных образцов проб песка с сопротивлением конусу ( qc ) зонда II типа этих же грунтов, выведена следующая корреляционная зависимость:
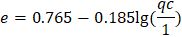
где 1 – это 1 МПа.
По утверждениям автора, коэффициент корреляции для такой зависимости составил 0,74, а среднее квадратическое отклонение – 0,09. Причем гранулометрический состав в таком случае практически не влияет на точность определения e .
Исходя из вышесказанного, получена формула количественного определения плотности p таких песков:
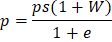
ps - плотность частиц грунта;
W - влажность грунта;
e – коэффициент пористости.
Если подставить в эту формулу коэффициент пористости, то получится следующее:
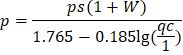
Т.к. для определения W и ps нет необходимости отбирать образцы ненарушенной структуры, то, по утверждениям автора, точности результатов p по данной формуле достаточно для расчетов оснований свайных фундаментов.
В следствии этого была представлена таблица, в которой приведены значения плотности p песков в зависимости от их qc и W .
Таблица 1. Значения плотности песков p в зависимости от сопротивления конусу зонда qc и влажности W по Мариупольскому

Для расчета значений в этой таблице, плотность частиц песков принималась, как средняя, ps =2,65 г/см 3 .
Это было небольшое отступление. В данном примере не рассматривается вариант применения такого расчета для определения плотности песков. Цель – показать возможность интерполяции по двум неизвестным, для которого хорошо подходит такая таблица.
Теперь перенесем ее на новый лист Excel. Чтобы еще немного усложнить задачу, расположим значения в строке qc от большего к меньшему. Соответственно, значения p тоже перенесем (рис. 14).

Далее ход действий такой же, как и в предыдущих примерах. Формат ячеек может быть, как общий, так и числовой.

Теперь обработаем результаты, а заодно рассчитаем такие показатели, как плотность сухого грунта pd , коэффициент пористости e и коэффициент водонасыщения Sr .

Дополнительно, помимо простой интерполяции, выполним расчет p по тем формулам, которые указывались выше:

Теперь, лист Excel у вас должен иметь следующий вид (рис. 15)

Изменяя значения в ячейках B1 , B2 и B3 , вы будете получать значения как по результатам интерполяции таблицы, так и по результатам расчета. Как вы можете заметить, они немного отличаются. Расчетные более точные, в том числе и потому, что указывается реальная плотность частиц, полученная в результате лабораторных исследований.

Выводы
В статье были предложены некоторые варианты для поиска и интерполяции значений. Конечно, их гораздо больше. Но уже с помощью этой информации вы самостоятельно сможете интерполировать любые таблицы или значения, которые найдете в нормативной документации или полученные в результате исследований. Без использования специального программного обеспечения, созданного для целей обработки геологической информации, можно вполне обойтись MS Office Excel.
В статистических и финансовых отчётах довольно часто используется такой показатель как удельный вес.
Удельный вес как статистический показатель рассчитывается в процентах и представляет собой долю отдельного компонента в общей совокупности (например, удельный вес несовершеннолетних в общей численности населения страны).

- Как рассчитать удельный вес в процентах
- Как рассчитать удельный вес продукции
- Как вычислить удельный вес
Формула и алгоритм расчёта удельного веса в процентах
Есть совокупность (целое), в состав которой входит несколько компонентов (составных частей).
Введём следующие обозначения:
X1, X2, X3, . Xn - части целого.
Они могут быть выражены в различных единицах измерения - рублях, штуках, килограммах и т.п.
Чтобы найти удельный вес каждой части совокупности (Wi) нужно воспользоваться следующей формулой:

То есть значение каждой части делится на общую сумму и умножается на 100 процентов.
Удельный вес будет показывать ценность, значимость или влияние каждого элемента совокупности.
Для проверки правильности расчётов нужно сложить все удельные веса между собой - их сумма должна быть равна 100 процентам.
Пример расчёта удельного веса в процентах
Компания в отчётном периоде выпустила 100000 тетрадей.
- тетради 12 листов - 30000 штук.
- тетради 18 листов - 10000 штук.
- тетради 24 листа - 10000 штук.
- тетради 48 листов - 30000 штук.
- тетради 96 листов - 20000 штук.
Требуется найти удельный вес каждого вида продукции.
Для решения данной задачи воспользуемся формулой, которая была приведена выше.
1) W1 (тетради 12 листов) = (30000 / 100000) * 100% = 0,3 * 100% = 30%.
2) W1 (тетради 18 листов) = (10000 / 100000) * 100% = 0,1 * 100% = 10%.
3) W1 (тетради 24 листа) = (10000 / 100000) * 100% = 0,1 * 100% = 10%.
4) W1 (тетради 48 листов) = (30000 / 100000) * 100% = 0,3 * 100% = 30%.
5) W1 (тетради 96 листов) = (20000 / 100000) * 100% = 0,2 * 100% = 20%.
Суммируем полученные удельные веса:
30% + 10% + 10% + 30% + 20% = 100%.
Это означает, что всё было посчитано правильно.
Расчёт удельного веса в программе Эксель (Excel)
Если совокупность включает в себя довольно большое число элементов, то удельный вес каждого элемента очень удобно рассчитывать с помощью программы Excel.
Вот как это можно сделать (на примере задачи про тетради):
1) Составляем таблицу, состоящую из 3 столбцов: 1 столбец - название, 2 столбец - значение, 3 столбец - удельный вес.

2) В ячейку D3 записываем формулу для удельного веса тетрадей 12 листов:
Ссылка на ячейку C8 является абсолютной, так как она будет фигурировать во всех формулах.
Устанавливаем процентный формат ячейки - для этого нажимаем на кнопку "%", расположенную на панели инструментов.

3) Для расчёта остальных удельных весов копируем формулу из ячейки D3 в нижестоящие ячейки (D4, D5 и т.д.).
При этом процентный формат будет применён к данным ячейкам автоматически, и его не нужно будет устанавливать.


Эта кнопка понадобится в том случае, когда удельный вес представляет собой дробь, и нужно отображать десятые и сотые доли.
Введем базовые понятия статистики, без которых невозможно объяснить более сложные понятия.
Генеральная совокупность и случайная величина
Пусть у нас имеется генеральная совокупность (population) из N объектов, каждому из которых присуще определенное значение некоторой числовой характеристики Х.
Примером генеральной совокупности (ГС) может служить совокупность весов однотипных деталей, которые производятся станком.
Поскольку в математической статистике, любой вывод делается только на основании характеристики Х (абстрагируясь от самих объектов), то с этой точки зрения генеральная совокупность представляет собой N чисел, среди которых, в общем случае, могут быть и одинаковые.
В нашем примере, ГС - это просто числовой массив значений весов деталей. Х – вес одной из деталей.
Если из заданной ГС мы выбираем случайным образом один объект, имеющей характеристику Х, то величина Х является случайной величиной . По определению, любая случайная величина имеет функцию распределения , которая обычно обозначается F(x).
Функция распределения
Функцией распределения вероятностей случайной величины Х называют функцию F(x), значение которой в точке х равно вероятности события X файл примера ):

В справке MS EXCEL Функцию распределения называют Интегральной функцией распределения ( Cumulative Distribution Function , CDF ).
Приведем некоторые свойства Функции распределения:
- Функция распределения F(x) изменяется в интервале [0;1], т.к. ее значения равны вероятностям соответствующих событий (по определению вероятность может быть в пределах от 0 до 1);
- Функция распределения – неубывающая функция;
- Вероятность того, что случайная величина приняла значение из некоторого диапазона [x1;x2): P(x 1 =0. Следовательно, плотность вероятности для непрерывной величины может быть, в отличие от Функции распределения, больше 1. Например, для непрерывной равномерной величины , распределенной на интервале [0; 0,5] плотность вероятности равна 1/(0,5-0)=2. А для экспоненциального распределения с параметром лямбда =5, значение плотности вероятности в точке х=0,05 равно 3,894. Но, при этом можно убедиться, что вероятность на любом интервале будет, как обычно, от 0 до 1.
Примечание : Площадь, целиком заключенная под всей кривой, изображающей плотность распределения , равна 1.
Примечание : Напомним, что функцию распределения F(x) называют в функциях MS EXCEL интегральной функцией распределения . Этот термин присутствует в параметрах функций, например в НОРМ.РАСП (x; среднее; стандартное_откл; интегральная ). Если функция MS EXCEL должна вернуть Функцию распределения, то параметр интегральная , д.б. установлен ИСТИНА. Если требуется вычислить плотность вероятности , то параметр интегральная , д.б. ЛОЖЬ.
Примечание : Для дискретного распределения вероятность случайной величине принять некое значение также часто называется плотностью вероятности (англ. probability mass function (pmf)). В справке MS EXCEL плотность вероятности может называть даже "функция вероятностной меры" (см. функцию БИНОМ.РАСП() ).
Вычисление плотности вероятности с использованием функций MS EXCEL
Понятно, что чтобы вычислить плотность вероятности для определенного значения случайной величины, нужно знать ее распределение.
Найдем плотность вероятности для стандартного нормального распределения N(0;1) при x=2. Для этого необходимо записать формулу =НОРМ.СТ.РАСП(2;ЛОЖЬ) =0,054 или =НОРМ.РАСП(2;0;1;ЛОЖЬ) .
Напомним, что вероятность того, что непрерывная случайная величина примет конкретное значение x равна 0. Для непрерывной случайной величины Х можно вычислить только вероятность события, что Х примет значение, заключенное в интервале (а; b).
Вычисление вероятностей с использованием функций MS EXCEL
1) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению (см. картинку выше), приняла положительное значение. Согласно свойству Функции распределения вероятность равна F(+∞)-F(0)=1-0,5=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(9,999E+307;ИСТИНА) -НОРМ.СТ.РАСП(0;ИСТИНА) =1-0,5. Вместо +∞ в формулу введено значение 9,999E+307= 9,999*10^307, которое является максимальным числом, которое можно ввести в ячейку MS EXCEL (так сказать, наиболее близкое к +∞).
2) Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению , приняла отрицательное значение. Согласно определения Функции распределения, вероятность равна F(0)=0,5.
В MS EXCEL для нахождения этой вероятности используйте формулу =НОРМ.СТ.РАСП(0;ИСТИНА) =0,5.
3) Найдем вероятность того, что случайная величина, распределенная по стандартному нормальному распределению , примет значение, заключенное в интервале (0; 1). Вероятность равна F(1)-F(0), т.е. из вероятности выбрать Х из интервала (-∞;1) нужно вычесть вероятность выбрать Х из интервала (-∞;0). В MS EXCEL используйте формулу =НОРМ.СТ.РАСП(1;ИСТИНА) - НОРМ.СТ.РАСП(0;ИСТИНА) .
Все расчеты, приведенные выше, относятся к случайной величине, распределенной по стандартному нормальному закону N(0;1). Понятно, что значения вероятностей зависят от конкретного распределения. В статье Распределения случайной величины в MS EXCEL приведены распределения, для которых в MS EXCEL имеются соответствующие функции, позволяющие вычислить вероятности.
Обратная функция распределения (Inverse Distribution Function)
Вспомним задачу из предыдущего раздела: Найдем вероятность, что случайная величина, распределенная по стандартному нормальному распределению, приняла отрицательное значение.
Вероятность этого события равна 0,5.
Теперь решим обратную задачу: определим х, для которого вероятность, того что случайная величина Х примет значение =НОРМ.СТ.ОБР(0,5) =0.

Однозначно вычислить значение случайной величины позволяет свойство монотонности функции распределения.
Обратите внимание, что для вычисления обратной функции мы использовали именно функцию распределения , а не плотность распределения . Поэтому, в аргументах функции НОРМ.СТ.ОБР() отсутствует параметр интегральная , который подразумевается. Подробнее про функцию НОРМ.СТ.ОБР() см. статью про нормальное распределение .

В англоязычной литературе обратная функция распределения часто называется как Percent Point Function (PPF).
Примечание : При вычислении квантилей в MS EXCEL используются функции: НОРМ.СТ.ОБР() , ЛОГНОРМ.ОБР() , ХИ2.ОБР(), ГАММА.ОБР() и т.д. Подробнее о распределениях, представленных в MS EXCEL, можно прочитать в статье Распределения случайной величины в MS EXCEL .
Рассмотрим Нормальное распределение. С помощью функции MS EXCEL НОРМ.РАСП() построим графики функции распределения и плотности вероятности. Сгенерируем массив случайных чисел, распределенных по нормальному закону, произведем оценку параметров распределения, среднего значения и стандартного отклонения .
Нормальное распределение (также называется распределением Гаусса) является самым важным как в теории, так в приложениях системы контроля качества. Важность значения Нормального распределения (англ. Normal distribution ) во многих областях науки вытекает из Центральной предельной теоремы теории вероятностей.
Определение : Случайная величина x распределена по нормальному закону , если она имеет плотность распределения :

СОВЕТ : Подробнее о Функции распределения и Плотности вероятности см. статью Функция распределения и плотность вероятности в MS EXCEL .
Нормальное распределение зависит от двух параметров: μ (мю) — является математическим ожиданием (средним значением случайной величины) , и σ ( сигма) — является стандартным отклонением (среднеквадратичным отклонением). Параметр μ определяет положение центра плотности вероятности нормального распределения , а σ — разброс относительно центра (среднего).
Примечание : О влиянии параметров μ и σ на форму распределения изложено в статье про Гауссову кривую , а в файле примера на листе Влияние параметров можно с помощью элементов управления Счетчик понаблюдать за изменением формы кривой.

Нормальное распределение в MS EXCEL
В MS EXCEL, начиная с версии 2010, для Нормального распределения имеется функция НОРМ.РАСП() , английское название - NORM.DIST(), которая позволяет вычислить плотность вероятности (см. формулу выше) и интегральную функцию распределения (вероятность, что случайная величина X, распределенная по нормальному закону , примет значение меньше или равное x). Вычисления в последнем случае производятся по следующей формуле:

Вышеуказанное распределение имеет обозначение N (μ; σ). Так же часто используют обозначение через дисперсию N (μ; σ 2 ).
Примечание : До MS EXCEL 2010 в EXCEL была только функция НОРМРАСП() , которая также позволяет вычислить функцию распределения и плотность вероятности. НОРМРАСП() оставлена в MS EXCEL 2010 для совместимости.
Стандартное нормальное распределение
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ=0 и дисперсией σ=1. Вышеуказанное распределение имеет обозначение N (0;1).
Примечание : В литературе для случайной величины, распределенной по стандартному нормальному закону, закреплено специальное обозначение z.
Любое нормальное распределение можно преобразовать в стандартное через замену переменной z =( x -μ)/σ . Этот процесс преобразования называется стандартизацией .
Примечание : В MS EXCEL имеется функция НОРМАЛИЗАЦИЯ() , которая выполняет вышеуказанное преобразование. Хотя в MS EXCEL это преобразование называется почему-то нормализацией . Формулы =(x-μ)/σ и =НОРМАЛИЗАЦИЯ(х;μ;σ) вернут одинаковый результат.
В MS EXCEL 2010 для стандартного нормального распределения имеется специальная функция НОРМ.СТ.РАСП() и ее устаревший вариант НОРМСТРАСП() , выполняющий аналогичные вычисления.
Продемонстрируем, как в MS EXCEL осуществляется процесс стандартизации нормального распределения N (1,5; 2).
Для этого вычислим вероятность, что случайная величина, распределенная по нормальному закону N(1,5; 2) , меньше или равна 2,5. Формула выглядит так: =НОРМ.РАСП(2,5; 1,5; 2; ИСТИНА) =0,691462. Сделав замену переменной z =(2,5-1,5)/2=0,5 , запишем формулу для вычисления Стандартного нормального распределения: =НОРМ.СТ.РАСП(0,5; ИСТИНА) =0,691462.
Естественно, обе формулы дают одинаковые результаты (см. файл примера лист Пример ).
Обратите внимание, что стандартизация относится только к интегральной функции распределения (аргумент интегральная равен ИСТИНА), а не к плотности вероятности .
Примечание : В литературе для функции, вычисляющей вероятности случайной величины, распределенной по стандартному нормальному закону, закреплено специальное обозначение Ф(z). В MS EXCEL эта функция вычисляется по формуле =НОРМ.СТ.РАСП(z;ИСТИНА) . Вычисления производятся по формуле

В силу четности функции плотности стандартного нормального распределения f(x), а именно f(x)=f(-х), функция стандартного нормального распределения обладает свойством Ф(-x)=1-Ф(x).
Обратные функции
Функция НОРМ.СТ.РАСП(x;ИСТИНА) вычисляет вероятность P, что случайная величина Х примет значение меньше или равное х. Но часто требуется провести обратное вычисление: зная вероятность P, требуется вычислить значение х. Вычисленное значение х называется квантилем стандартного нормального распределения .
В MS EXCEL для вычисления квантилей используют функцию НОРМ.СТ.ОБР() и НОРМ.ОБР() .
Графики функций
В файле примера приведены графики плотности распределения вероятности и интегральной функции распределения .

Как известно, около 68% значений, выбранных из совокупности, имеющей нормальное распределение , находятся в пределах 1 стандартного отклонения (σ) от μ(среднего или математического ожидания); около 95% - в пределах 2-х σ, а в пределах 3-х σ находятся уже 99% значений. Убедиться в этом для стандартного нормального распределения можно записав формулу:
которая вернет значение 68,2689% - именно такой процент значений находятся в пределах +/-1 стандартного отклонения от среднего (см. лист График в файле примера ).
В силу четности функции плотности стандартного нормального распределения: f ( x )= f (-х) , функция стандартного нормального распределения обладает свойством F(-x)=1-F(x). Поэтому, вышеуказанную формулу можно упростить:
Для произвольной функции нормального распределения N(μ; σ) аналогичные вычисления нужно производить по формуле:
Вышеуказанные расчеты вероятности требуются для построения доверительных интервалов .
Примечание : Для построения функции распределения и плотности вероятности можно использовать диаграмму типа График или Точечная (со сглаженными линиями и без точек). Подробнее о построении диаграмм читайте статью Основные типы диаграмм .
Примечание : Для удобства написания формул в файле примера созданы Имена для параметров распределения: μ и σ.
Генерация случайных чисел
С помощью надстройки Пакет анализа можно сгенерировать случайные числа, распределенные по нормальному закону .
СОВЕТ : О надстройке Пакет анализа можно прочитать в статье Надстройка Пакет анализа MS EXCEL .
Сгенерируем 3 массива по 100 чисел с различными μ и σ. Для этого в окне Генерация случайных чисел установим следующие значения для каждой пары параметров:

Примечание : Если установить опцию Случайное рассеивание ( Random Seed ), то можно выбрать определенный случайный набор сгенерированных чисел. Например, установив эту опцию равной 25, можно сгенерировать на разных компьютерах одни и те же наборы случайных чисел (если, конечно, другие параметры распределения совпадают). Значение опции может принимать целые значения от 1 до 32 767. Название опции Случайное рассеивание может запутать. Лучше было бы ее перевести как Номер набора со случайными числами .
В итоге будем иметь 3 столбца чисел, на основании которых можно, оценить параметры распределения, из которого была произведена выборка: μ и σ . Оценку для μ можно сделать с использованием функции СРЗНАЧ() , а для σ – с использованием функции СТАНДОТКЛОН.В() , см. файл примера лист Генерация .

Примечание : Для генерирования массива чисел, распределенных по нормальному закону , можно использовать формулу =НОРМ.ОБР(СЛЧИС();μ;σ) . Функция СЛЧИС() генерирует непрерывное равномерное распределение от 0 до 1, что как раз соответствует диапазону изменения вероятности (см. файл примера лист Генерация ).
Задачи
Задача1 . Компания изготавливает нейлоновые нити со средней прочностью 41 МПа и стандартным отклонением 2 МПа. Потребитель хочет приобрести нити с прочностью не менее 36 МПа. Рассчитайте вероятность, что партии нити, изготовленные компанией для потребителя, будут соответствовать требованиям или превышать их. Решение1 : = 1-НОРМ.РАСП(36;41;2;ИСТИНА)
Задача2 . Предприятие изготавливает трубы, средний внешний диаметр которых равен 20,20 мм, а стандартное отклонение равно 0,25мм. Согласно техническим условиям, трубы признаются годными, если диаметр находится в пределах 20,00+/- 0,40 мм. Какая доля изготовленных труб соответствует ТУ? Решение2 : = НОРМ.РАСП(20,00+0,40;20,20;0,25;ИСТИНА)- НОРМ.РАСП(20,00-0,40;20,20;0,25) На рисунке ниже, выделена область значений диаметров, которая удовлетворяет требованиям спецификации.

Решение приведено в файле примера лист Задачи .
Задача 4 . Нахождение параметров нормального распределения по значениям 2-х квантилей (или процентилей ). Предположим, известно, что случайная величина имеет нормальное распределение, но не известны его параметры, а только 2-я процентиля (например, 0,5- процентиль , т.е. медиана и 0,95-я процентиль ). Т.к. известна медиана , то мы знаем среднее , т.е. μ. Чтобы найти стандартное отклонение нужно использовать Поиск решения . Решение приведено в файле примера лист Задачи .
Примечание : До MS EXCEL 2010 в EXCEL были функции НОРМОБР() и НОРМСТОБР() , которые эквивалентны НОРМ.ОБР() и НОРМ.СТ.ОБР() . НОРМОБР() и НОРМСТОБР() оставлены в MS EXCEL 2010 и выше только для совместимости.
Линейные комбинации нормально распределенных случайных величин
Известно, что линейная комбинация нормально распределённых случайных величин x ( i ) с параметрами μ ( i ) и σ ( i ) также распределена нормально. Например, если случайная величина Y=x(1)+x(2), то Y будет иметь распределение с параметрами μ (1)+ μ(2) и КОРЕНЬ(σ(1)^2+ σ(2)^2). Убедимся в этом с помощью MS EXCEL.
С помощью надстройки Пакет анализа сгенерируем 2 массива по 100 чисел с различными μ и σ.

Теперь сформируем массив, каждый элемент которого является суммой 2-х значений, взятых из каждого массива.
С помощью функций СРЗНАЧ() и СТАНДОТКЛОН.В() вычислим среднее и дисперсию получившейся выборки и сравним их с расчетными.
Кроме того, построим График проверки распределения на нормальность ( Normal Probability Plot ), чтобы убедиться, что наш массив соответствует выборке из нормального распределения .

Прямая линия, аппроксимирующая полученный график, имеет уравнение y=ax+b. Наклон кривой (параметр а) может служить оценкой стандартного отклонения , а пересечение с осью y (параметр b) – среднего значения.
Для сравнения сгенерируем массив напрямую из распределения N (μ(1)+ μ(2); КОРЕНЬ(σ(1)^2+ σ(2)^2) ).
Как видно на рисунке ниже, обе аппроксимирующие кривые достаточно близки.

В качестве примера можно провести следующую задачу.
Задача . Завод изготавливает болты и гайки, которые упаковываются в ящики парами. Пусть известно, что вес каждого из изделий является нормальной случайной величиной. Для болтов средний вес составляет 50г, стандартное отклонение 1,5г, а для гаек 20г и 1,2г. В ящик фасуется 100 пар болтов и гаек. Вычислить какой процент ящиков будет тяжелее 7,2 кг. Решение . Сначала переформулируем вопрос задачи: Вычислить какой процент пар болт-гайка будет тяжелее 7,2кг/100=72г. Учитывая, что вес пары представляет собой случайную величину = Вес(болта) + Вес(гайки) со средним весом (50+20)г, и стандартным отклонением =КОРЕНЬ(СУММКВ(1,5;1,2)) , запишем решение = 1-НОРМ.РАСП(72; 50+20; КОРЕНЬ(СУММКВ(1,5;1,2));ИСТИНА) Ответ : 15% (см. файл примера лист Линейн.комбинация )
Аппроксимация Биномиального распределения Нормальным распределением
Если параметры Биномиального распределения B(n;p) находятся в пределах 0,1 10, то Биномиальное распределение можно аппроксимировать Нормальным распределением .
При значениях λ >15 , Распределение Пуассона хорошо аппроксимируется Нормальным распределением с параметрами: μ =λ , σ 2 = λ .
Подробнее о связи этих распределений, можно прочитать в статье Взаимосвязь некоторых распределений друг с другом в MS EXCEL . Там же приведены примеры аппроксимации, и пояснены условия, когда она возможна и с какой точностью.
СОВЕТ : О других распределениях MS EXCEL можно прочитать в статье Распределения случайной величины в MS EXCEL .
Читайте также:


