Как сделать треугольные полигоны
Перед вами четыре абсолютно чистых окна проекции в 3ds Max, и в этих полях вам предстоит создавать с нуля сложные модели. Это сначала кажется удивительным: как из ничего сделать целый объект?
Один из инструментов такой 3D-магии — Editable Poly. Он позволяет из отдельных частей — полигонов — формировать абсолютно любые формы (проводить полигональное моделирование).
Подробно рассмотрим все основные инструменты работы с ним, а также решение популярных проблем.
Содержание
Что такое полигоны в 3D-моделировании?
В процессе моделирования какого-либо объекта специалист выстраивает его форму из полигонов — плоских геометрических фигур, состоящих из точек, которые соединены между собой рёбрами.
Совокупность полигонов, из которых вырисовывается фигура, называют полигональной сеткой.
Понятие Editable Poly
- Edit Poly — это модификатор;
- Editable Poly — конвертация в редактируемые полигоны с помощью встроенных инструментов в 3ds Max.
Также есть важное отличие: если результат изменений не устроил, Edit Poly можно удалить, и сцена вернется к первоначальному виду, до применения модификатора. В случае с Editable Poly придется либо все начинать сначала, либо долго применять команду отмены действия (Ctrl+Z).
Работа с полигонами
Хороший 3D-моделлер должен уметь сделать из набора точек и граней абсолютно любой объект, будь то картонная коробка или сложный элемент декора. Поэтому ему нужно знать, как работают функции редактирования полигонов и полигональной сетки.
При создании сложных объектов чертеж просто необходим. Например, смоделировать автомобиль без него практически невозможно.
Рассмотрим инструменты, которые применяют в работе с полигонами в 3ds Max.
- Vertex (вершины) — точки в пространстве.
- Edge (рёбра) — линии. Образовываются, если соединить две точки.
- Border (граница).
- Polygon (полигон). Образовывается путём соединения трёх и более рёбер.
- Element (элемент). Работа с этим инструментом происходит в ситуациях, когда нужно выделить полностью весь объект.
За выбор каждого конкретного подобъекта отвечают горячие клавиши 1, 2, 3, 4 и 5 (в соответствии с порядком в списке).
При выборе какого-либо подобъекта программа 3ds Max его подсвечивает в окне проекции.
Список необходимых инструментов находится в меню справа.
Selection
- по вершине (by Vertex) — выделяются полигоны/рёбра, в которые входит выбранная вершина;
- по углу (by Angle) — выделяет все полигоны, которые находятся в рамках заданного угла; этот инструмент работает исключительно в режиме Polygons;
- игнорировать задний план (ignore Backfacing) — при выборе не будут учитываться подобъекты, которых не видно с конкретного ракурса.
- Grow — выделяет полигоны, расположенные вокруг выбранного;
- Shrink — позволяет сократить количество выбранных полигонов;
- Ring — выделяет все ребра, расположенные параллельно выбранному (работает только в режиме Edge);
- Loop — выделяет соседние с выбранным рёбра по цепочке.
Soft Selection
- Falloff — задать область выделения;
- Bubble — округлить выделенную область;
- Pinch —заострить выделенную область.
Edit Vertices
Edit Edges
- Remove;
- Extrude
- Weld;
- Chamfer (в этом свитке инструмент Chamfer имеет ряд настраиваемых параметров, включая размер, скругление, выбор вида и многое другое);
- Connect.

- Split создает разрез по линии выбранного ребра.
- Bridge соединяет полигонами ребра.
Edit Borders
- Chamfer;
- Extrude;
- Bridge;
- Connect.
Edit Polygons
- Bevel выполняет ту же функцию, что и Extrude (выдавливание или вдавливание), однако впоследствии форму образованной области можно менять (например, задать её скос);
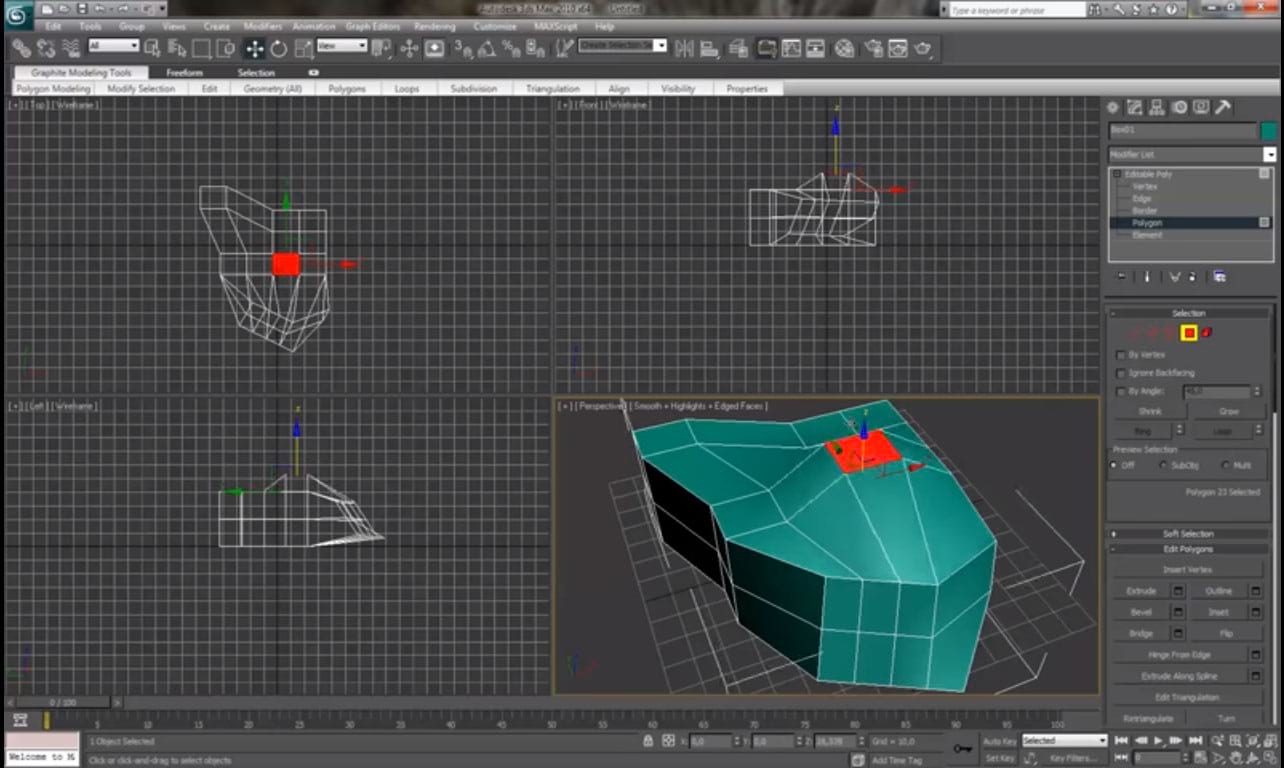
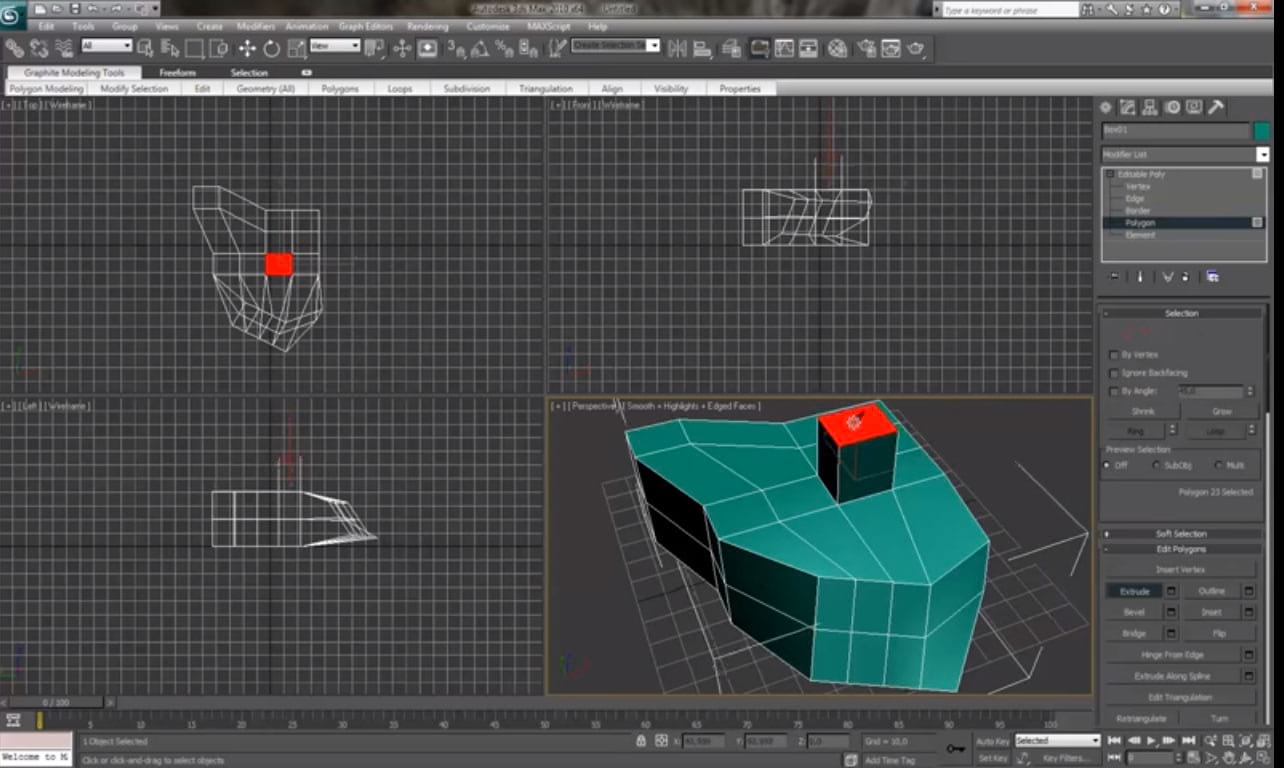
А вот как работает Bevel: можно не просто выдавить полигон, но и почти без ограничений менять его форму — сужать, расширять, вращать и даже выворачивать
- Outline сужает или расширяет выбранный полигон или полигоны;
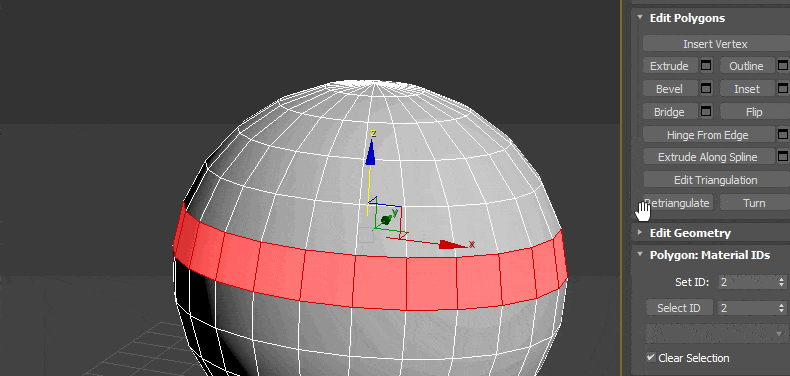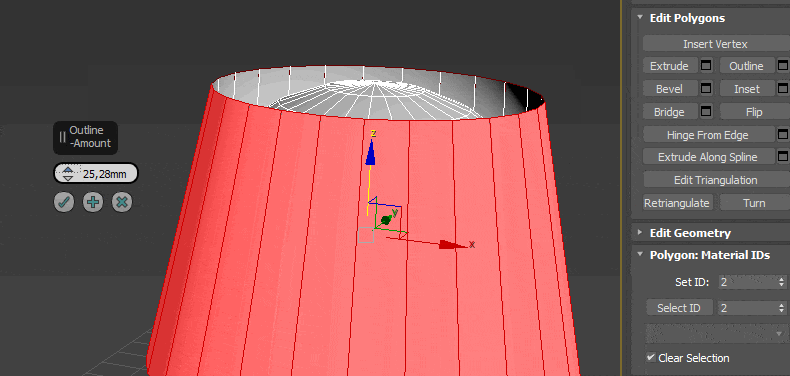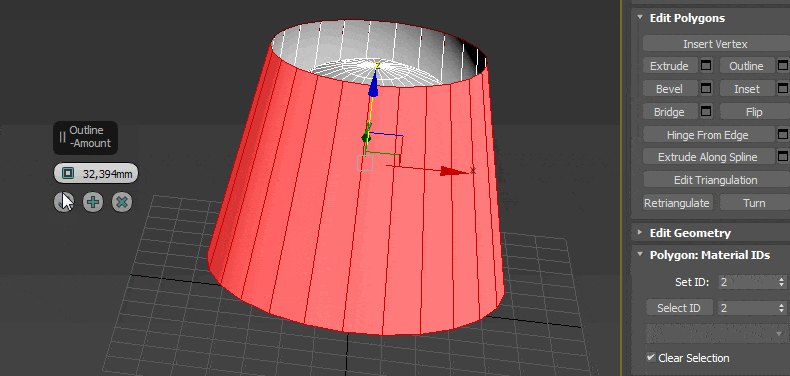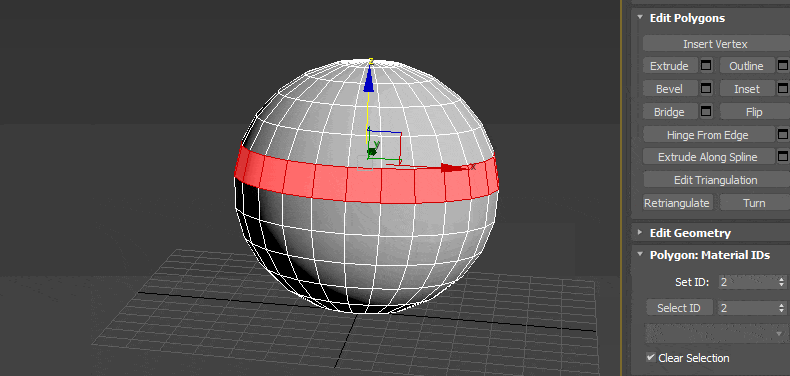
- Inset образовывает на поверхности выбранного полигона ещё один, но меньшего размера;
- Flip выворачивает наизнанку выбранные полигоны.
Edit Geometry
- С помощью Attach объединяют между собой две модели или два подобъекта. Detach позволяет их разъединить.
- Cut разрезает в указанном направлении полигон.
- Slice Plane показывает плоскость, которая позволит нарезать поверхность.
- Collapse удаляет полигон, а на его месте собирает все близлежащие вершины в одной точке.
- MSmooth применяется для сглаживания или, наоборот, детализации.
- С помощью кнопок X, Y и Z задаются точные координаты подобъектов на оси.
Решение распространённых проблем
Время от времени в процессе полигонального моделирования возникают сложности, за решением которых приходится идти на форумы и советоваться с коллегами.
Но не всем комфортно общаться с абсолютно незнакомыми людьми.
Ученики школы 3D CLUB имеют возможность сначала обсудить появившиеся проблемы между собой или проконсультироваться с нашими кураторами.
Кроме этого, на этапе обучения преподаватели делимся огромным количеством лайфхаков по оптимизации своей работы, которые сами собирали много лет на своих заказах.
Некоторые фишки и полезные советы выкладываем в открытый доступ, для всех.
Руководитель школы 3D CLUB Семен Потамошнев рассказал, как новичкам в 3D-дизайне стоит относиться к правкам, чтобы расти как специалист:

Поговорим о сетках треугольников. Сетки квадратов используются практически повсюду, от пикселей изображения до расположения домов в квартале. Сетки шестиугольников представлены тоже довольно широко, особенно в настольных играх. Однако сетки треугольников (равномерное заполнение 2D-плоскости равносторонними треугольниками) почему-то не очень популярны. Я встречал заявления, что они бесполезны, или что у них сложная математика. Но этой статьёй я докажу, что оба заявления ошибочны: вычисления на самом деле проще, чем при работе с шестиугольниками, к тому же треугольники обладают множеством преимуществ.
Все вычисления я выполнил в своём коде на github, однако стоит объяснить, как и зачем нужно использовать такие сетки.
Когда я говорю о сетке треугольников, то подразумеваю тайловую карту, в которой все тайлы являются одинаковыми равносторонними треугольниками, выстроенными в переменные строки (или столбцы).

Важно здесь то, что каждая ячейка имеет ровно трёх соседей. Иногда встречаются игры, где отрисована сетка треугольников, но на самом деле фигуры расположены в углах. Каждый угол соединяется с шестью другими, то есть на самом деле это сетка не треугольников, а шестиугольников.
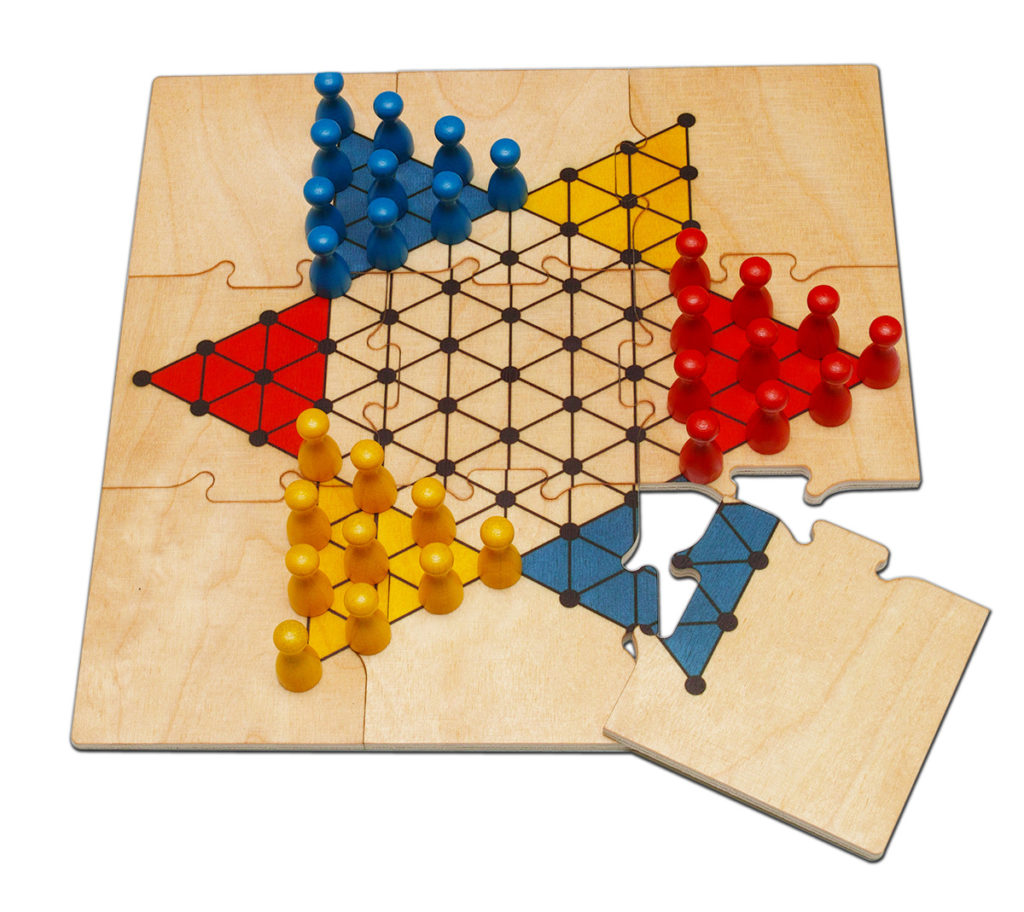
В китайские шашки (Халма) играют на сетке шестиугольников, стилизованной на фотографии под сетку треугольников.
И наоборот: если в игру играют на углах сетки шестиугольников, то на самом деле это сетка треугольников. Из-за этого свойства равномерные сетки шестиугольников и треугольников называют двойными.
Зачем использовать сетки треугольников
Треугольники обладают тремя потрясающими свойствами:
- Они всегда планарны
- Они просты
- Их геометрия более удобна
Планарность
Если выбрать любые три точки в трёхмерном пространстве, то через них всегда можно прочертить плоскость. То есть имея эти три точки, всегда можно нарисовать треугольник на поверхности этой плоскости. Для многоугольников с большим количеством вершин это не всегда верно. Если взять четыре 3D-вершины, то соединить их в многоугольник с четырьмя вершинами однозначным образом становится сложно. Страдающие подобной проблемой многоугольники называются непланарными, и в компьютерной графике они могут становиться серьёзной помехой, поэтому почти вся графика реального времени преобразует все объекты в треугольники.
Даже несмотря на то, что мы будем говорить о заполнении 2D-пространства, это свойство всё равно для нас полезно на случай, если мы захотим добавить карту высот. В сетке треугольников каждая вершина может располагаться на своей высоте, но в сетке не будет возникать проблем. Если проделать подобное с сеткой квадратов, то мы сразу же столкнёмся с появлением непланарных вершин.

В Sim City 2000 использовались сетки квадратов и карты высот. Обратите внимание, что многие наклонные тайлы разделены на пары треугольников, потому что тайл непланарен.

Карта высот сетки треугольников. Никаких проблем с наклонами.
Простота
Математически понятно, что 3 меньше, чем 4 или 6. Это наименьшее количество вершин, которое может иметь многоугольник, поэтому треугольники — самая лучшая фигура для любого алгоритма, масштабирующегося в зависимости от количества точек или рёбер.
Например, в своём туториале по Marching Cubes я говорил, что для учёта всех случаев в 2D требуется создать различных тайлов. Так получается потому, что у каждого из четырёх углов есть два варианта. Треугольники имеют два варианта: смотрящий вверх и вниз, то есть для двух вариантов требуется по разных тайлов. То есть в обоих случаях получаем 16 тайлов.
Но это самый простой случай. Если мы допускаем возможность поворота тайлов, то вариантов у треугольников становится меньше (4 против 6). А если нам нужно больше чем два возможных значения в каждом из углов (54 против 81 или 10 против 21 с поворотами/отражениями).

Поворачиваемые тайлы, необходимые для marching cubes
Кроме того, треугольники хороши для линейных интерполяций. Три значения по треугольнику можно легко интерполировать при помощи барицентрических координат, в то время как квадратам требуется билинейная интерполяция, которая более сложна. Именно из-за этой разницы был изобретён симплекс-шум в качестве замены шуму Перлина — они работают одинаково, однако в симплекс-шуме используется сетка треугольников (в случае 2D).
Геометрия лучше, чем у шестиугольников

При работе с шестиугольниками быстро понимаешь, что кучу неудобств доставляют их рёбра. Они не выстраиваются в прямую линию! Из-за этого невозможно разделить сетку линей. Невозможно собрать большой шестиугольник из множества маленьких.
В следующем разделе мы активно будем использовать прямые линии рёбер для понимания того, как работают сетки треугольников.
Хотя нужно признать, что у сеток треугольников есть собственные геометрические неудобства, в основном связанные с тем, как нужно обрабатывать треугольники, смотрящие в разных направлениях.
Как использовать сетки треугольников
Примечание: в данном туториале в основном рассматриваются концепции и идеи, а не методы и код. Если вам интереснее реализация, то изучите написанную мной справочную реализацию.
Хитрость заключается в том, чтобы воспринимать сетку треугольников как задаваемую тремя множествами равномерно расположенных параллельных линий, наложенных друг на друга:

Пространство между каждой из этих параллельных линий называется полосами. Мы обозначим три направления полос как a, b и c, а сами полосы пронумеруем по порядку.

Тогда координатой треугольника будут три целых числа a, b, c, определяющие, в каких полосах находится треугольник. Всё очень просто!

Стоит заметить, что в такой системе нет треугольника с координатами (0, 0, 0). Я пронумеровал полосы таким образом, что точкой начала координат является вершина, окружённая шестью треугольниками в полосах 0 и 1. При другой нумерации полос система работает так же.
Соседи
Когда мы переходим с одного треугольника на другой, то пересекаем одну из линий, разделяющих полосы. Я создал такую систему, что при перемещении из треугольника, указывающего вершиной вниз, мы прибавляем к координате единицу. А при выходе из треугольника вершиной вверх — вычитаем единицу.

Центр треугольника
Так как перемещение в соседний треугольник всегда является шагом заданного размера по одной из трёх полос, заданный треугольник можно найти, просто просуммировав все шаги, сделанные в трёх направлениях.

Расстояние между треугольниками
Так как каждый шаг меняет координату на единицу, формула расстояния представляет собой всего лишь разность в каждой из координат.
В следующей статье я рассмотрю альтернативную функцию расстояния.
В каком треугольнике находится точка
Чтобы найти треугольник, содержащий заданную точку, нужно просто определить, в каких трёх полосах находится треугольник. Это можно сделать, измерив расстояние, перпендикулярное к полосе из точки начала координат, что легко выполняется при помощи скалярного произведения с последующим усечением значения до целого числа.
ceil округляет число вверх до ближайшего целого, а floor округляет вниз. Нельзя просто округлить все три полосы в одном направлении, иначе возникнут сложности, например, с точкой с координатой (0, 0), которая находится в углу шести разных треугольников.
Другие операции
С сеткой можно проделать множество других операций, например, измерять расстояния, рисовать линии и выполнять повороты. Всё это подробно описано в моей справочной реализации на github.
Можете сравнить её с реализацией сетки шестиугольников. С треугольниками работать намного проще, чем с шестиугольниками, поэтому я реализовал многие операции с шестиугольниками, сначала выполняя эквивалентную операцию с треугольниками, а затем преобразуя их в шестиугольники.
Надеюсь, я убедил вас, что сетки треугольников — недооценённый инструмент.
Процедурная генерация сетки треугольников, выполненная Tessera
Дополнительные материалы
Статья RedBlobGaming о сетках по-прежнему остаётся лучшим ресурсом для изучения сеток. Я слышал, что он работает над обновлённой версией.
Также могу порекомендовать вам статью Джастина Помбрио о преобразовании из пикселей в шестиугольники, из которой я узнал, как удобно работает система треугольников и как она связана с сетками шестиугольников.
Как мы выяснили в прошлой части, современные трехмерные компьютерные игры строятся на основе полигонов. Но, что же это за зверь такой?
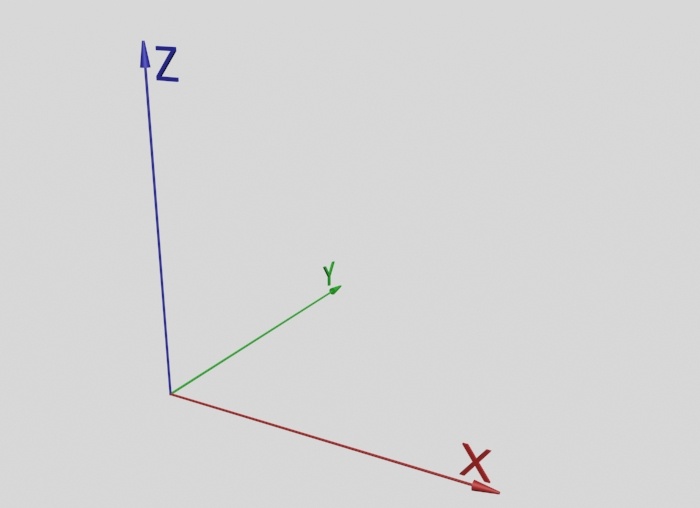
Полигон (Polygon) – это плоскость в евклидовом пространстве. Пространство имеет размерность три, соответственно, имеются три координаты: X, Y, Z. Условно их можно обозвать как длина, высота и глубина. В программном обеспечении для 3D нет единого стандарта относительно, так сказать, ориентации данных координат, хотя, как правило, координата X параллельна условном горизонту, т.е. это длина, а вот условной высотой может быть как Y так и Z. Соответственно, условной глубиной может быть как Z, так и Y. Но нам это не столь суть важно, примем для последующего материала представление, показанное ниже.
У полигона есть вершины, минимум три, максимум, теоретически, бесконечность. Практически максимум – много. Но в играх используются треугольные полигоны, т.е. полигон имеет три вершины. Почему именно три? Через три точки в пространстве можно провести только одну плоскость, что упрощает расчеты и позволяет избежать искажений (артефактов) на итоговой картинке связанных с тем, что вершины полигона могут лежать не в одной плоскости.
Однако в программах трехмерного моделирования принято пользоваться 4-х угольными полигонами, а вот 5-ти и больше, как правило, под запретом. Поэтому при моделировании приходится следить за тем, чтобы все 4 вершины полигона были в одной или почти одной плоскости. А как же игры? спросите вы. Полигон с 4-мя вершинами математически очень просто превратить в два треугольных с двумя общими вершинами, что и делается автоматически при экспорте в игровой движок.
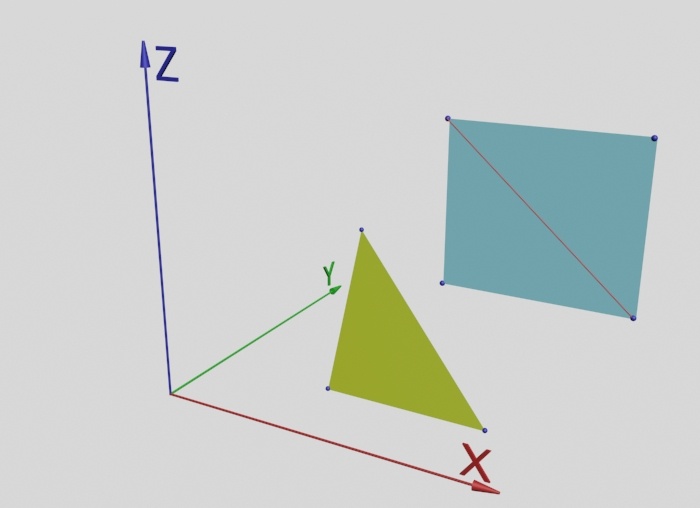
На рисунке ниже показаны треугольный полигон и четырехугольный, условно разделенный на два треугольных. На изображении это прямоугольный треугольник и прямоугольный параллелограмм, но по факту полигон может иметь различные длины сторон, соответственно, и различные углы между ними. Хотя стараются, по возможности, все стороны делать приблизительно одинаковыми, это называется равномерная полигональная сетка.
Почему сетка? Из полигонов создаются трехмерные объекты для игр (и не только), и если рассматривать все эти полигоны издалека включив отображение сторон полигона, они же ребра, то все это похоже на сетку.
При моделировании, тестировании и т.п. для закрашивания плоскости между вершинами полигона используется произвольный цвет, но зачастую это так называемый сермат, RGB 128,128,128. На нем удобно тестировать, в частности, освещение. Да и однородная заливка, в отличии от полновесных текстур, использует не так много ресурсов компьютера.
Приведенный выше рисунок показывает как, на самом деле, с помощью плоских поверхностей создаются объекты практически любой формы. Правило тут простое: чем меньше каждый полигон, тем более точно можно передать форму исходного объекта. Это как с мозаикой, про которую разговор был в первой части. Но и увеличивать до бесконечности количество полигонов тоже нельзя, так как это сказывается на производительности, ведь компьютеру желательно не менее 30 раз в секунду пересчитать положение каждой, по крайней мере видимой зрителю, вершины полигона. Но и эти расчеты лишь малая часть того, что видеокарта в сотрудничестве с ЦП делают для расчета финальной картинки. Но об этом мы поговорим в следующих частях.
Кроме координат вершин есть у полигона такое свойство как нормаль. Это вектор, перпендикулярный одной из сторон плоскости полигона. Так как это вектор, то у него есть направление. Это направление указывает лицевую сторону полигона, вернее его начало находится у лицевой стороны полигона. Нужна нормаль для наложения текстур и расчета освещенности. Так же хочу заметить, что математически полигон не имеет никакого отношения к тому, как он выглядит, т.е. к текстурам. Полигон отдельно, текстуры – отдельно.
То же можно наблюдать, если попасть туда, куда игровой персонаж попадать не должен по задумке разработчиков: за уступы скал, в закрытые помещения и т.п. И это не баг игрового движка, это его особенность, ну, и недосмотр при тестировании (или разработчики не отреагировали должным образом на отчет тестировщиков). Необходима такая особенность для оптимизации расчетов итоговой картинки, или, по-другому, рендеринга. Ведь совсем незачем тратить вычислительные ресурсы на то, что никто никогда увидеть не должен.
Внимательный читатель может спросить: а как же быть в том случае, если игровой персонаж должен зайти в помещение? Тогда необходимо, как и в реальном здании, придавать стенам (потолку, крыше, дверям и т.д.) толщину с помощью двух полигонов у которых нормали смотрят в противоположные стороны.
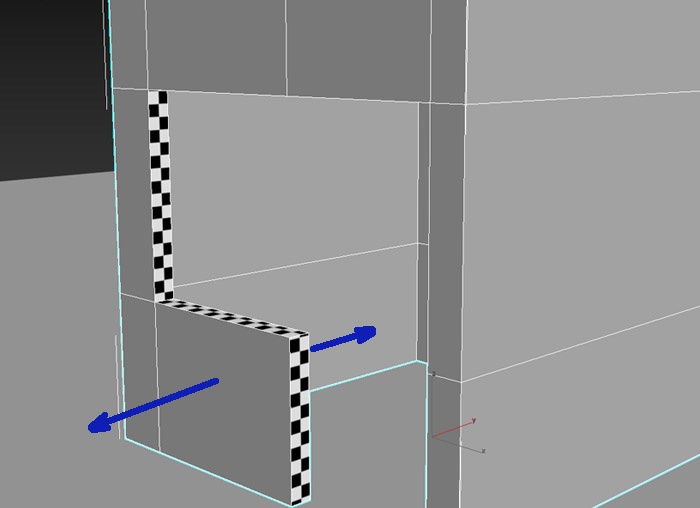
Ниже показан фрагмент модели здания со стеной, имеющей реальную толщину. Синим показано направление нормали у полигонов.
Для совсем тонких предметов, таких как лист бумаги, применяется другой подход и зависит он от конкретного игрового движка. Например, может применяться специальный двухсторонний материал или отключаться параметр Backface culling, и в этом случае объект будет выглядеть одинаково с обеих сторон. (Подробнее про Backface culling можно почитать тут: Полигоны, свободная камера и MGS 5)
Теперь поговорим о том, какие бывают трехмерные полигональные модели.
3D модели принято делить на низкополигональные (low poly) и высокополигональные (high poly). Как несложно догадаться – разница в количестве полигонов, причем разница не абсолютная, а, как и все в нашем мире, относительная.
Высокополигональной можно назвать модель с самодостаточной геометрией, т.е. когда даже мелкие детали (в разумных, конечно, пределах) смоделированы с помощью полигонов и при этом модель выглядит достаточно правдоподобно даже без текстур. Непосредственно в играх high poly модели, как правило, не применяются, однако они необходимы в процессе разработки 3D игры, о чем будет рассказано ниже.
Высокополигональные модели применяются для статического рендеринга, например интерьерной визуализации или предметной, когда необходимо фотореалистичное качество и большие разрешения итоговой картинки. Для получения такого изображения используются специальные программы рендеринга и просчет одного кадра может занимать несколько десятков часов, поэтому в играх это неприменимо.
Низкополигональные модели применяются в основном в играх или для анимации, когда визуальный реализм не имеет первостепенного значения. Есть два основных способа получения низкополигональной модели: непосредственное моделирование с прицелом на малое количество полигонов или упрощение высокополигональной модели. То же справедливо и для high poly моделей (если не брать в расчет 3D сканирование): их получают путем усложнения и добавления полигонов низкополигональной модели, либо моделируют сразу из расчета максимально необходимого количества полигонов. Какой подход применятся в том или ином случае зависит от многих факторов, как то: геометрии самой модели, применяемого программного обеспечения, наличия похожих моделей, принятого в студии-разработчике порядка разработки, предпочтений 3D-художника и т.п.
Хочу особо обратить внимание на то, что разделение на high poly и low poly очень и очень относительно. Зависит от многих факторов, и одна и та же модель может быть как низкополигональной, так и высокополигональной. Например, для игры для ПК была разработана высокополигональная модель персонажа, затем из нее получили низкополигональную, условно, уменьшив количество полигонов в два раза. А позже решили портировать игру на мобильные устройства. И количество полигонов, опять же, условно, для этого сократили в четыре раза по сравнению с изначальной моделью, или в два раза по сравнению с моделью для ПК-версии игры. Ведь мобильные устройства мало того, что не такие мощные, как ПК, так еще и размер экрана не позволяет различить мелкие детали, поэтому такая высокая детализация, как для полноразмерного монитора, там попросту не нужна.

Ниже показаны сферы одинакового диаметра с различным количеством полигонов.
Да и с каждым новым процессором, каждой новой видеокарточкой мощность компьютерного железа растет, соответственно, и в играх получается отображать в кадре все больше и больше полигонов без ущерба производительности.

Ниже представлена эволюция полигональной Лары Крофт.
Как же получают 3D модели? Традиционно для этого используется полигональное моделирование в специальных программных пакетах, как то: 3ds Max, Maya, Cinema 4D и т.п. В последнее время к разработке также подключают программы для так называемой трехмерной лепки, к примеру ZBrush и 3D-Coat. Ну, и с развитием технологии 3D сканирования, модели получают путем этого самого сканирования с последующей оптимизацией полигональной сетки.

Если используется традиционное полигональное моделирование, то 3D художнику необходимо от чего-то отталкиваться. Для этого используются так называемые референсы, или, по-другому, изображения того, что необходимо смоделировать. Это могут быть фотографии (для реальных предметов или персонажей), концепт-арты (для вымышленных), или даже существующие объекты. К примеру, необходимо смоделировать существующие кубики Lego. Самая в данном случае хорошая идея – иметь их под рукой и моделировать, непосредственно вертя в руках эти самые кубики.
Ниже изображение референса и 3D модели (без текстур).
Теперь вернемся к вопросу: а зачем при разработке 3D игры иметь в наличии сразу две модели одного и того же объекта — high poly и low poly? Высокополигональная модель непосредственно в игре использоваться не будет, но она необходима для такого важного процесса, как запекание текстур. Так называют подготовку целого ряда текстур или, как их еще называют, карт. Это обычные файлы изображений (с необычными, на первый взгляд, рисунками в них) цель которых как можно реалистичнее представить модель в игре и взять на себя, так сказать, часть геометрии. По сути – это создание 3D иллюзии там, где добиться этого полигонами сложно, неподъемно по производительности или просто нецелесообразно.
Возьмем, к примеру, старую доску. В ней может быть множество трещин и мелких сколов. В реальности это перепад высот (или глубин) материала самой доски. И, по-хорошему, полигоны также должны повторять эти перепады. Но тогда модель может оказаться настолько высокополигональной, что никакое железо не потянет это количество полигонов. Поэтому для начала моделируют как можно более подробную высокополигональную модель этой самой доски, а затем с помощью специальных программ генерируют (запекают) карты высот, затенения и т.п. для имитации этих самых трещин и сколов на низкополигональной модели.

Ниже упрощенно схематически показано как смешивание запеченных с high poly модели карт, в сочетании с текстурой дерева, в результате дает реалистичное изображение.
Ведь как мы различаем эти самые трещинки и сколы? По изменению яркости и цвета текстуры дерева благодаря тому, что свет по-разному отражается от неровностей поверхности, а кое-где и отбрасывает тень. К тому уже, в трещинах, как правило, накапливается грязь и т.п. Все это и позволяет нам отличить старую древесину от новой. Вот эти эффекты и запекаются в файлы изображений. Такой прием позволяет создавать довольно реалистичные объекты с использованием значительно меньшего количества полигонов. При отображении объекта в игре эти карты накладываются друг на друга по определенным алгоритмам, что и создает иллюзию наличия геометрии, которой на самом деле то и нет.
Это мы забежали немного вперед, затронув тему текстур, но без этого трубно было бы объяснить необходимость на один игровой объект делать как минимум две модели.

Если уж мы говорим про 3D в играх, то следует обязательно упомянуть такую технологию, как LOD, сокращенно от Level of Detail, она же уровень детализации. Суть ее сводится к тому, что в зависимости от того, насколько тот или иной объект близко располагается от игрового персонажа, или какой процент высоты экрана занимает, то используются модели с различного рода детализацией. Опять же, все ради оптимизации. Чем ближе к виртуальной камере тот или иной объект, тем более детализированная модель подставляется. На практике часто количество таких моделей ограничивается тремя: для переднего, среднего и заднего планов. И обозначаются, как правило: LOD_0, LOD_1, LOD_2. Это все варианты низкополигональной игровой модели.
Вот, наверно, вкратце и все про полигоны. Если остались необозначенные или нераскрытые моменты – пишите про это в комментариях.
По идее, далее необходимо продемонстрировать этот самый процесс полигонального моделирования, дабы наглядно показать, как это делается. И пример должен быть не очень простой, ради показа хотя бы нескольких приемов моделирования, но и не очень сложный, чтобы не нагонять сон на зрителя. Я думал-думал над предметом моделирования и пришел к выводу, что модель керосиновой лампы неплохо впишется в данную концепцию. Но, дабы не утомлять читателя, решил собственно процесс моделирования вынести в третью, или, если хотите, в 2,5 часть повествования, которую надеюсь опубликовать в ближайшем будущем.

Метод полигонального моделирования основан на манипуляциях с гранями, вершинами и ребрами объектов. Именно с помощью editable poly в 3d max создается и редактируется большинство моделей, которые мы используем в интерьерах и экстерьерах. В сегодняшнем уроке мы рассмотрим основные инструменты полигонального моделирования.
Что такое полигоны
Итак, каждый трехмерный объект состоит из плоскостей: полигонов. А они в свою очередь разбиты на треугольники: Faces, однако, последние для нашего удобства скрыты и не отображаются в видовом окне по умолчанию. Да и речь сегодня пойдет не о них. А вот чтобы яснее понять, что такое polygons, создадим бокс, разобьем его на любое количество сегментов и переведем его в Editable Poly. Жмем на него ПКМ/Convert to/Convert to Editable Poly. Именно с этого всегда начинается работа с полигонами.
Также, к объекту можно просто применить модификатор Edit Poly из выпадающего списка модификаторов. При таком способе всегда можно будет вернутся к изначальной форме. Однако, это слегка нагружает компьютер, потому лучше использовать первый способ.

Заметим, что справа в окошке появилось название модификатора. Если отжать плюсик, то мы увидим его подобъекты, которые можно редактировать.



Подобъекты дублируются внизу в свитке Selection, как иконки. Удобно и то, что за ними закреплены горячие клавиши 1, 2, 3, 4 и 5 — соответственно их порядку в списке.

Свиток Selection
Под иконками, в свитке Selection, можно также найти способы выделения для каждого из подобъектов:
- By Vertex (по вершине) — выделяются ребра или полигоны (не работает с вершинами), которые включают в себя выбранную точку;

- Ignore Backfacing (игнорировать задний план) — при выборе будут игнорироваться vertex (edges, polygons), которые не видно на данном ракурсе;
- By Angle (по углу) — работает только в режиме Polygons и выделяет все полигоны, находящиеся в пределах заданного угла;
А теперь о кнопках:
- Grow — выделяет все полигоны, окружающие выделенный;
- Shrink — действует противоположно;
- Ring — работает с edge. Выделяет цепочку ребер;
- Loop — также выделяет цепочку, но по другому принципу.
Все эти элементы (vertex, polygons, edges и др.) можно редактировать, передвигать, увеличивать, разрезать и проделывать множество других операций. Для того чтобы это сделать, для каждого подобъекта есть кнопки. Они находятся в свитке внизу. Давайте кратко разберем их.
Vertex. Edit Vertices
Переходим в режим Vertex или жмем 1 на клавиатуре.

- Remove – с помощью кнопки можно удалить вершину.
Чтобы удалить точку, можно воспользоваться кнопкой backspace на клавиатуре. А вот delete удалит не только вершину, но и поверхности, примыкающие к ней.
- Break — команда разъединяет вершины в данной точке;
- Extrude — выдавливает точку, при этом получается зубец, пирамида;
- Weld — одна из самых полезных кнопок. Позволяет соединить (склеить) вершины, находящиеся на заданном расстоянии;
- Chamfer — образует срез на вершине;
- Connect — с помощью этой кнопки можно добавить ребро между двумя выбранными вершинами.
Edges. Edit Edges
Переходим в режим Edges или жмем 2 на клавиатуре.

- Bridge – позволяет соединить ребра полигонами;
- Connect – очень важная и нужная кнопка. Если выделить два противоположных ребра на одном полигоне, и нажать на нее, четко посередине создается дополнительное ребро. Таким образом плоскость можно разбить на равные части по горизонтали или вертикали. Изменить количество и расстояние между новыми ребрами можно, нажав на квадратик рядом с кнопкой (по умолчанию создается 1 ребро).
Border. Edit Borders
Переходим в режим Edges или жмем 3 на клавиатуре.
- Bridge – образует соединение между кромками;
- Connect – аналогично инструменту в Edges.
Polygon. Edit Polygons.
Переходим в режим Polygons или жмем 4 на клавиатуре.

- Extrude – позволяет выдавливать или вдавливать полигон на заданную величину;
- Outline – расширяет/сужает полигон;
- Bevel – похож на Extrude, но позволяет кроме высоты выдавливания/вдавливания задать площадь скоса;
- Inset – создает на поверхности полигон меньшего размера;
- Bridge – создает мостик между полигонами;
- Flip – позволяет вывернуть полигоны наизнанку.
Вот и все основные кнопки, помогающие создавать и редактировать полигональные объекты. Кстати, всегда стоит помнить, что добавление полигонов в большом количестве неизбежно приводит к перегрузке сцены и ее торможению. Потому все лишнее лучше удалять, упрощая модель. Посмотреть количество полигонов в сцене можно нажав клавишу 7 на клавиатуре. Счетчик показывает и количество точек — Verts. Отключается его отображение той же кнопкой.

Свиток Edit Geometry
Этот свиток есть в режиме редактирования любого подобъекта, так как относится к редактированию общей геометрии. В нем есть и еще несколько интересных кнопок:
Читайте также:


