Как сделать теорему пифагора в паскале
Здравствуйте, дорогие друзья. Сегодня мы рассмотрим известную всем со школьной скамьи теорему Пифагора на языке программирования Python. Наверное одна из самых лёгких теорем, при помощи которой можно было получить "5" по геометрии. И я думаю, все помнят крылатое выражение "Пифагоровы штаны во все стороны равны". Итак, давайте взглянем на исходный код. Внимательно читаем все комментарии:
А теперь запускаем программу:
Как видим, мы запустили программу три раза: первый - находили катет из известного нам катета и гипотенузы, второй - находили гипотенузу из двух катетов и третий раз мы вводили любую цифру, кроме 1 или 2, соответственно программа выдаёт ошибку, т.к. у нас только два варианта в программе.
На этом у меня на сегодня всё. Также предлагаю ознакомиться с другими моими работами по Python (ссылки ниже) и подписаться на наш Ютуб-канал ПиМ [ZveKa] . До новых встреч на просторах Яндекс Дзена.
Написать линейную программу для нахождения гипотенузы треугольника.

Надо составить программу для вычисления гипотенузы, площади и периметра прямоугольного треугольника
Надо составить программу для вычисления гипотенузы, площади и периметра прямоугольного треугольника.
Написать подпрограмму процедуру нахождения гипотенузы С и площади S прямоугольного треугольника
Люди помогите,нужно нарешать 3 задачи( ну или одну какую-то из них) вот 1) Написать подпрограмму.

Написать программу, вычисляющую значение гипотенузы прямоугольного треугольника
Значение катетов вводятся с клавиатуры пожалуйста помогите

Нахождения гипотенузы прямоугольного треугольника
Написать программу которая находит гипотенузу треугольника по введеным катетам
Hitoku, не спорю) Но ведь смешно: когда я сказал моему преподавателю информатики, что в Паскале можно делать вычисления, не объявляя переменные, то у него глаза на лоб вылезли.
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь или здесь.
написать программу найти площадь треугольника найти длину гипотенузы теоремой пифагора
написать программу найти площадь треугольника найти длину гипотенузы решить способом теорема.
Составить программу определения гипотенузы, площади, периметра прямоугольного треугольника
Составить программу определения гипотенузы, площади, периметра прямоугольного треугольника по.

Составить программу для нахождения площади треугольника S, по двум сторонам
День добрый. Помогите пожалуйста составить программу. Задание: Составить программу для.
Составить программу в виде подпрограммы функции для нахождения площади треугольника
Составить программу в виде подпрограммы функции для нахождения площади треугольника с заданными его.

составить программу нахождения периметра треугольника по заданным координатам его вершин,используя подпрограмму нахождения растояния между двумя точк.
составить программу для нахождения периметра треугольника по заданным координатам его.
Задача Пифагора
ифагор заказал ремесленнику изготовить несколько прямоугольных треугольников из ценных пород дерева для использования на занятиях по геометрии, но ремесленник перепутал размеры, и треугольники получились не прямоугольные. Чтобы не выбрасывать испорченный ценный материал, ремесленник решил переделать получившиеся треугольники в прямоугольные, постаравшись максимизировать их площади.
Требуется написать программу, которая по размерам сторон треугольника находит максимальную площадь прямоугольного треугольника, который можно вырезать из этого треугольника.
В выходной файл OUTPUT.TXT выведите максимальную площадь прямоугольного треугольника, получаемого из заданного треугольника, с точностью не хуже, чем 10-5.

Теорема Пифагора
Условие:вводится значение 2 катетов треугольника надо найти гипотенуза треугольника. Зарание спасибо

генератор чисел Пифагора
Друзья, мне дали задачу индивидуальную, но я не разобрался с ней! Я её не понял 🙁 Обьясните.
Теорема Пифагора в Паскале
Напишите программу которая вычисляет теорему пифагора при вводе сторон ab,bc,ac под корнем.
Таблица Пифагора для N чисел
Составить программу вывода на экран таблицы Пифагора для N чисел.
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь или здесь.

Напечатать все числа Пифагора
Натуральные числа а, b, с называются числами Пифагора, если выполняется условие a^2+b^2=с^2.

Вывод на экран таблицы Пифагора
1. Известно A:=’ *** *** ‘ B:=’*** *** ***’ Получить на экране *** ***.

Напечатать все числа Пифагора, меньше N
Всем привет! Сабж: «Натуральные числа abc называются числами Пифагора, если выполняется условие.
Теорема Пифагора: Вычислить расстояниями между всеми точками массива
Заданно N точек на плоскости. Построить матрицу расстояний между всеми точками
На плоскости заданы n точек своими координатами. Построить матрицу расстояний между всеми точками.
Построить матрицу расстояний между всеми точками. Найти равноудаленные точки, если такие есть
Помогите, пожалуйста, выполнить задание. Насколько я понял, оно должно выполняться через двумерные.

Построить матрицу расстояний между всеми точками. Найти равноудаленные точки, если такие есть, и напечатать их номера
Всем привет. Помогите написать программу. На плоскости заданы n точек своими координатами.
На пальцах: в типе real более 300 значащих цифр (из которых используются старшие 16 цифр), а в типе longint не более 10 значащих цифр.
Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь или здесь.
Теорема Пифагора
вот кодprocedure TForm1.Button1Click(Sender: TObject); var a, b, c : Integer; begin a :=.

Теорема Пифагора
Условие:вводится значение 2 катетов треугольника надо найти гипотенуза треугольника. Зарание спасибо
Теорема Пифагора
Составить программу,которая графически иллюстрирует теорему Пифагора.

Теорема пифагора
Доброго времени суток, есть теорема Пифагора a2= b2+ c2−2bc ·cos(A) я пытаюсь ее перенести в.
Теорема Пифагора
Разработать программу с графическим интерфейсом. Пользователь выбирает два элемента прямоугольного.
Теорема пифагора в паскале
Теорема Пифагора гласит:
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
Формулы теоремы Пифагора

Доказательство теоремы Пифагора
Площадь прямоугольного треугольника вычисляется по формуле:
Для вычисления площади произвольного треугольника формула площади:
Потом приравниваем правые части обеих формул для площади треугольника:
Обратная теорема Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b и c, такой, что
существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Доказана она ученым математиком и философом Пифагором.
Значение теоремы в том, что с ее помощью можно доказать другие теоремы и решать задачи.
Дополнительный материал: Теорема о сумме углов треугольника
Простой пример проверки треугольника. Является ли треугольник прямоугольным.
Тоже самое, но при помощи массива:
А теперь при помощи Case:
Если заранее не известны стороны (гда какая). Переделаем первый код:
. дельфи код на теорему пифагора теорема пифагора в паскале теорема пифагора паскаль
По двум введенным пользователем катетам вычислить длину гипотенузы.
Катеты и гипотенуза — это стороны прямоугольного треугольника. Если известны длины катетов, то длина гипотенузы находится по теореме Пифагора:
С помощью формулы это выражается так:
c 2 = a 2 + b 2
Отсюда следует, что длина гипотенузы равна квадратному корню из суммы квадратов катетов:
c = sqrt(a 2 + b 2 )
(sqrt() — обозначение функции извлечения корня).
Обычно в языках программирования предусмотрен оператор возведения в степень. Например, в языке программирования Python он обозначается двумя звездочками (**), а в Basic знаком ^. Однако в Pascal нет операции возведения в степень.
Для извлечения корня обычно существует специальная функция, а не оператор.
Доказательства теоремы Пифагора
Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.
Теорема Пифагора — краткая история
Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.
Формулировка теоремы
Изначальная (геометрическая) формулировка Пифагора гласила:
В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Позднее появился алгебраический вариант:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.
Уравнение
В виде формулы теорема Пифагора записывается следующим образом:
Доказательство через подобные треугольники
Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.
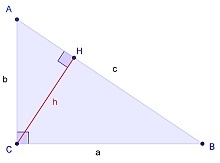
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:
CB 2 =ABxHB, AC 2 =ABxAH
Сложив между собой квадраты катетов, получаем:
AC 2 +CB 2 =ABx(HB+AH)=AB 2
Это и требовалось доказать.
Другие способы доказательства теоремы
Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.
Методом площадей
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:
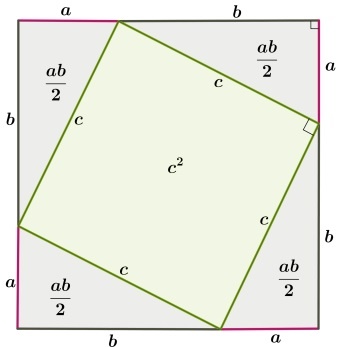
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.
Площадь внешнего квадрата включает в себя:
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.
Методом бесконечных малых
Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.
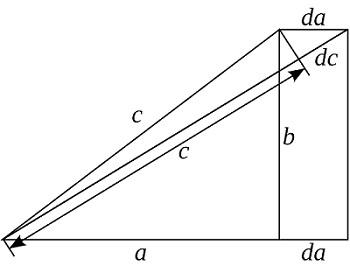
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем
Разделяя переменные составляется дифференциальное уравнение:
Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:
определяя из начальных условий константу интегрирования, получим:
a = 0 ⇒ c 2 = b 2 = const
Таким образом мы определяем, что
Следствие из теоремы Пифагора
Его так же называют обратной теоремой Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.
В алгебраическом виде это можно представить так:
c2=a2+b2, где:
Применение теоремы
Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.
Расстояние между точками
Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:
Евклидова метрика
В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:
Теория чисел
Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.
Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.
Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.
Примеры решения задач
Задача 1
В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.
Решение
Для нахождения ответа подставим в формулу исходные значения:
Задача 2
Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.
Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:
Задача 3.
Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.
Решение
Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.
В общем есть один человек, который утверпждает, что теорему Пифагора можно доказать через закон Паскаля. При этом доказательство привести открзывается, ссылается на то, что это была оплимпиадная задача.
По этому вопрос, кто-нибудь знает можно ли доказать теорему Пифагора через закон Паскаля, и была ли эта задача на каких-нибудь олимпиадах?
Срочно иду в гараж выводить теорему Пифагора с помощью гидравлического пресса. И ещё: может под большим давлением пространство искривляется. Тогда как в нем сформулировать теорему Пифагора? Например, Лобачевский пытался экспериментально наблюдать искривление пространства, того не ведая, что его геометрия реализуется в пространстве скоростей СТО.
Под давлением чего? Пространство может менять кривизну в присутствии массы, давление тут как-то не причём.
Собственно это меня и настараживает, что теорема Пифагора говорит о свойствах отрезков на плоскости а теорема Паскаля о изотропии жидкости.
Да просто вы любом пространстве, у которого метрическая матрица не единичная теорема Пифагора не верна. А Сформулировать её там можно как раз таки заданием метрики.
Скажите хотя бы, хоть кто-нибудь, кроме меня, считает, что это сделать невозможно?
Последний раз редактировалось myhand 17.08.2011, 19:42, всего редактировалось 1 раз.
Да просто вы любом пространстве, у которого метрическая матрица не единичная теорема Пифагора не верна.
Я вот зато точно знаю, что к физике этот вопрос отношения не имеет. Подходит такой ответ? Математические теоремы не доказываются физическими экспериментами.
Последний раз редактировалось drozdov_mihail 17.08.2011, 20:02, всего редактировалось 1 раз.
Под давлением чего? Пространство может менять кривизну в присутствии массы, давление тут как-то не причём.
Ну, например, под большим давлением белый карлик образовался: вечером пойду с собачкой гулять и проверю сиё предположение с помощью гидравлического пресса в гараже.
Я про то, что Лобачевский умер в 1856 году. Да, в геометрии Лобачевского, на плоскости кривизны - 1, теорема Пифагора имеет вид ch a = ch b ch c
Последний раз редактировалось drozdov_mihail 17.08.2011, 20:15, всего редактировалось 1 раз.
Комп - это такая штука, о которой можно говорить, что она постоянно находится в стадии физического эксперимента. Я, например, прежде чем доказывать некоторые свои опусы, прогонял их через комп.
Комп - это такая штука, о которой можно говорить, что она постоянно находится в стадии физического эксперимента
С тем же успехом можно говорить, что том, что чайник находится в стадии физического эксперемента. Да и какое это имеет отношение к теме?
Какая у него "метрическая матрица" - не знаю, ввиду того что сей термин изобретен Вами. А вот метрический тензор у него - не обязательно единичный или вообще постоянный. Смотря какие координаты выбрать.
Задумайтесь еще вот над чем:
Школу прогуляли, когда планиметрию проходили? Там как-то без метрики, без координат вообще обходились ;)
Комп - это такая штука, о которой можно говорить, что она постоянно находится в стадии физического эксперимента.
Нет, нельзя. Вне зависимости от того как Вы свои опусы привыкли "доказывать" - хоть просто в носу ковыряйтесь. К физическому эксперименту функционирование цифровых ЭВМ никакого отношения не имеет.

Площадь прямоугольного треугольника вычисляется по формуле:
Для вычисления площади произвольного треугольника формула площади:
- p – полупериметр. p=frac (a+b+c) ,
- r – радиус вписанной окружности. Для прямоугольника r=frac (a+b-c).
Потом приравниваем правые части обеих формул для площади треугольника:
2 ab = left( (a+b)^ -c^
ight)
Обратная теорема Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2 ,
существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Доказана она ученым математиком и философом Пифагором.
Значение теоремы в том, что с ее помощью можно доказать другие теоремы и решать задачи.
Дополнительный материал: Теорема о сумме углов треугольника
Простой пример проверки треугольника. Является ли треугольник прямоугольным.
Тоже самое, но при помощи массива:
А теперь при помощи Case:
Если заранее не известны стороны (гда какая). Переделаем первый код:
. дельфи код на теорему пифагора теорема пифагора в паскале теорема пифагора паскаль
По двум введенным пользователем катетам вычислить длину гипотенузы.
Катеты и гипотенуза — это стороны прямоугольного треугольника. Если известны длины катетов, то длина гипотенузы находится по теореме Пифагора:
"Квадрат гипотенузы равен сумме квадратов катетов"
С помощью формулы это выражается так:
c 2 = a 2 + b 2
Отсюда следует, что длина гипотенузы равна квадратному корню из суммы квадратов катетов:
c = sqrt(a 2 + b 2 )
(sqrt() — обозначение функции извлечения корня).
Обычно в языках программирования предусмотрен оператор возведения в степень. Например, в языке программирования Python он обозначается двумя звездочками (**), а в Basic знаком ^. Однако в Pascal нет операции возведения в степень.
Для извлечения корня обычно существует специальная функция, а не оператор.

Площадь прямоугольного треугольника вычисляется по формуле:
Для вычисления площади произвольного треугольника формула площади:
- p – полупериметр. p=frac (a+b+c) ,
- r – радиус вписанной окружности. Для прямоугольника r=frac (a+b-c).
Потом приравниваем правые части обеих формул для площади треугольника:
2 ab = left( (a+b)^ -c^
ight)
Обратная теорема Пифагора:
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2 ,
существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника. Доказана она ученым математиком и философом Пифагором.
Значение теоремы в том, что с ее помощью можно доказать другие теоремы и решать задачи.
Дополнительный материал: Теорема о сумме углов треугольника
Простой пример проверки треугольника. Является ли треугольник прямоугольным.
Тоже самое, но при помощи массива:
А теперь при помощи Case:
Если заранее не известны стороны (гда какая). Переделаем первый код:
. дельфи код на теорему пифагора теорема пифагора в паскале теорема пифагора паскаль
По двум введенным пользователем катетам вычислить длину гипотенузы.
Катеты и гипотенуза — это стороны прямоугольного треугольника. Если известны длины катетов, то длина гипотенузы находится по теореме Пифагора:
"Квадрат гипотенузы равен сумме квадратов катетов"
С помощью формулы это выражается так:
c 2 = a 2 + b 2
Отсюда следует, что длина гипотенузы равна квадратному корню из суммы квадратов катетов:
c = sqrt(a 2 + b 2 )
(sqrt() — обозначение функции извлечения корня).
Обычно в языках программирования предусмотрен оператор возведения в степень. Например, в языке программирования Python он обозначается двумя звездочками (**), а в Basic знаком ^. Однако в Pascal нет операции возведения в степень.
Для извлечения корня обычно существует специальная функция, а не оператор.
Читайте также:


