Как сделать таблицу истинности по информатике 8 класс
• личностные — понимание роли фундаментальных знаний как основы современных информационных технологий.
Решаемые учебные задачи:
1) проверка знания основных логических операций;
2) закрепление навыков формализации логических выражений;
3) рассмотрение алгоритма построения таблиц истинности;
4) отработка навыков построения таблиц истинности для логических выражений.
Основные понятия, рассматриваемые на уроке:
Средства ИКТ, используемые на уроке:
• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
Электронное приложение к учебнику:
• презентация “Элементы алгебры логики”.
Федеральный центр информационных образовательных ресурсов:
1) информационный модуль “Построение отрицания к простым высказываниям, записанным на русском языке”;
2) практический модуль “Построение отрицания к простым высказываниям, записанным на русском языке”;
3) контрольный модуль “Построение отрицания к простым высказываниям, записанным на русском языке”.
Особенности изложения содержания темы урока
В начале урока осуществляется:
1) визуальная проверка выполнения заданий в РТ;
2) рассмотрение заданий, вызвавших затруднения при выполнении домашнего задания;
3) экспресс-проверка (в течение 5 минут) у учеников знания основных логических операций — соответствующие таблицы истинности ученики записывают на листочках и сдают их учителю.
Далее рекомендуется проработать информационный и практический модули ФЦИОР “Построение отрицания к простым высказываниям, записанным на русском языке”; выполнить № 6, 7 и 11 к параграфу.
Новый материал излагается в сопровождении презентации “Элементы алгебры логики”, в процессе изложения материала выполняется задание № 8 к параграфу 1.3.
§ 1.3 (пункт 3); задание № 10 к параграфу; задание № 83 в РТ.
Дополнительное задание: работа с практическим модулем ФЦИОР “Построение отрицания к простым высказываниям, записанным на русском языке”.
Указания, комментарии, ответы и решения
Задания в учебнике
6) Ане не нравятся уроки математики или Ане не нравятся уроки химии.
7) Неверно, что Ане нравятся уроки математики и химии.
8) Неверно, что Ане нравятся уроки математики или химии.
9) Неверно, что Ане нравятся уроки математики и не нравятся уроки химии.
№ 7. Так как по запросу сомики&гуппи найдено 0 сайтов, то с помощью кругов Эйлера условие задачи можно представить так:

Чтобы найти количество сайтов, соответствующих запросу сомики|меченосцы|гуппи, к количеству элементов множества сомики (250) добавим количество элементов множества меченосцы без сомиков (200 - 20), а также гуппи без меченосцев (500 - 10). Получаем: 250 + 180 + 490 = 920.
Практически любое цифровое устройство включает в себя логические элементы. На информатике в 8 классе изучают так называемую алгебру логики. Эта наука используется при создании автоматических устройств, аппаратных и информационных вычислительных блоков. По сути, такие элементы реализуют функции сложения, умножения и инверсии дискретного сигнала, являясь преобразователями. Причём их работа поясняется так называемой таблицей истинности.
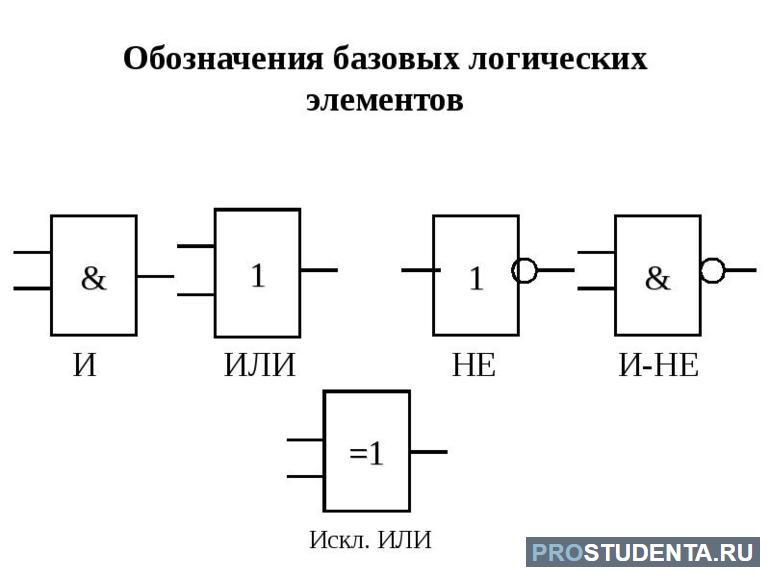
Общие сведения
Одним из простых типов данных в информатике считается булевый. Этот примитивный вид может принимать два возможных значения истинный или ложный. В международной системе для описания используются слова true и false. Своё название тип получил благодаря английскому математику Джорджу Буля изучающий логику математических операций. В общем случае под ним понимают действие, соответствующее некому высказыванию. То есть с её помощью получают сложные выражения из простых и используют результат для управления последовательности определённых программ.
Наиболее часто в языках программирования применяется числовой тип описания. В них считается, что ноль соответствует логической лжи, а единица — истинности. Это даёт возможность использовать действия, выбрав отдельные биты с помощью побитовых операций. Среди них наиболее известны следующие:
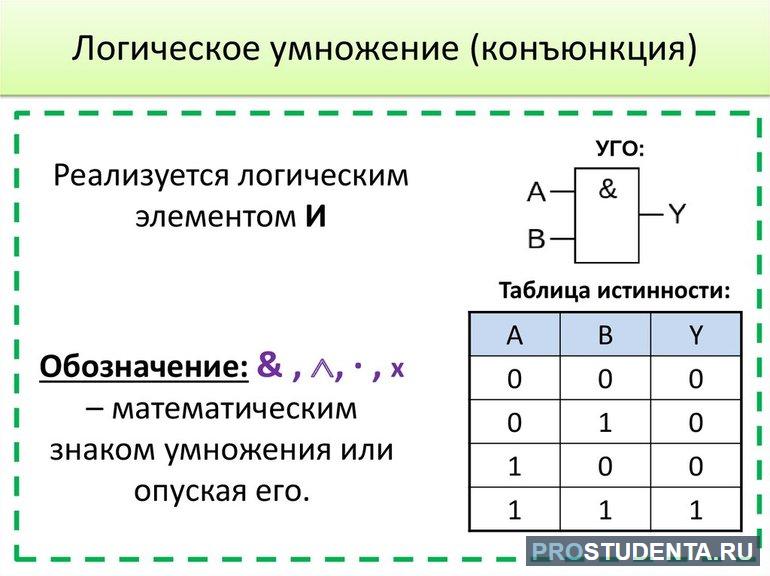
Для реализации логических действий используются электрические схемы, называемые логическими элементами. В качестве данных используются сигналы с разным уровнем напряжения. На вход схемы подаётся значение, принимаемое за ноль или единицу, а с выхода снимается другое с определённым уровнем. То есть используется двоичная система счисления. Напряжение высокого значения принимается как истина, а низкого считается за ложь. Логические схемы позволяют в наглядном графическом виде отобразить последовательность операций при вычислении логических формул.
Такие логические элементы используют для организации работы компьютеров, схем автоматического контроля. Поэтому для любых видов сигналов характерны дискретные величины. При этом сам элемент может иметь как один, так и несколько входов, два или один выход. Традиционно элементы логики изготавливают в виде радиодеталей. Это интегральные микросхемы разного размера.
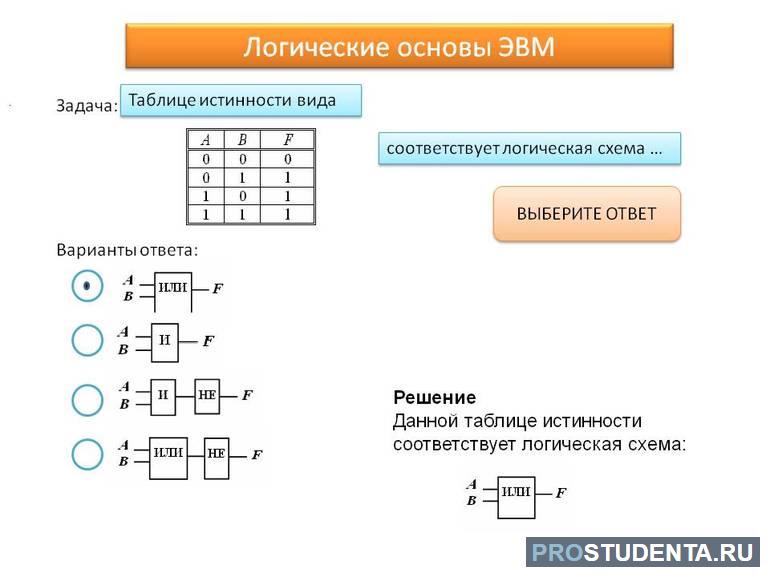
Таблица истинности
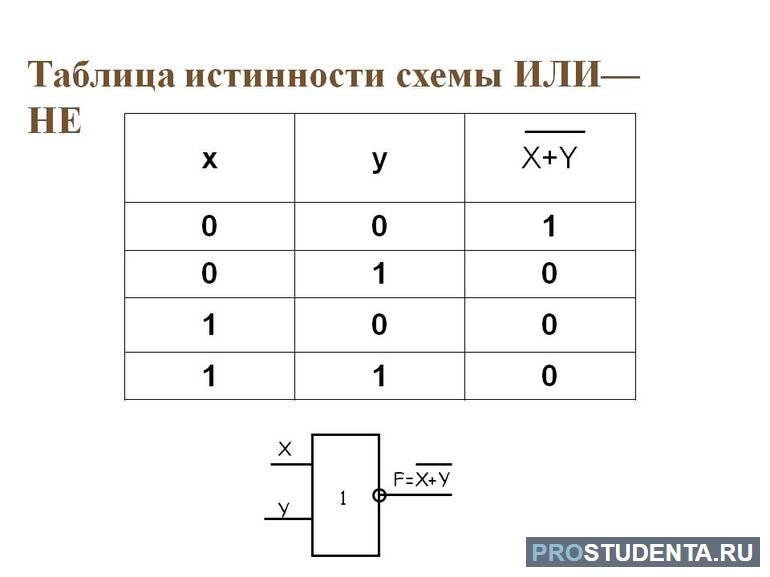
Таблица истинности содержит все возможные комбинации переменных на входе и соответствующий результат их на выходе. Состоит она из 2 n строк, где n — количество переменных, и n + m столбцов, у которых m — выходные данные. Если все строки известны, то исследуемый элемент, включающий функцию, называют частично определённый. Количество существующих операций зависит от числа высказываний. Если содержится 2 n строк, то и всевозможных комбинаций будет 2 n соответствующих значениям аргументов.
Строится таблица по простому принципу. В столбцах указываются номера входов и выходов, а строки заполняют соответствующими цифрами. Например, пусть имеется логический элемент с тремя выводами. Два из них входа X1 и X2, а один выход Y1. При подаче высокого напряжения сразу на два входных контакта на выходе устанавливается низкий уровень. В ином же случае всегда будет высокий. Для такой ситуации в первых двух столбцах проставляется все возможные варианты. Их будет четыре. В последней же колонке, советующей выходу, ставятся везде нули, кроме строчки, состоящей из двух единиц.
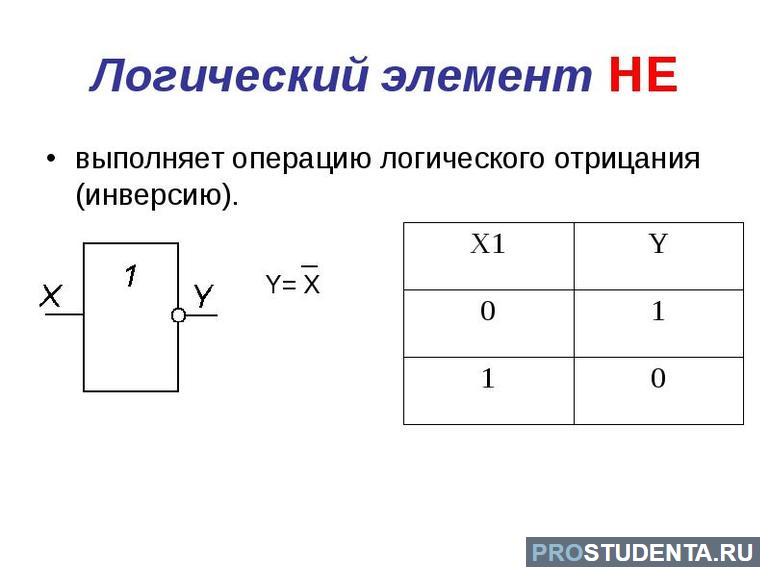
Построенная таблица является законченной основной характеристикой логического элемента. Работать с ней довольно удобно, так как наглядно и без дополнительных пояснений видно, какие сигналы установятся на выходе. Иногда есть смысл строить истинность для той или иной функции, используя лишь определённый набор заданных операций. Существует несколько возможностей описания:
- дизъюнктивная;
- конъюнктивная;
- алгебраическая нормальная.
Простой конъюнкцией называется система переменных, где каждая из них встречается только один раз. Если же объединить дизъюнкции с помощью конъюнкции, то можно получить совершённую конъюнктивную нормальную форму. В обратном случае возникнет дизъюнктивная составляющая.
Простейшие логические выражения
Любое утверждение строится из высказываний. Например, забор красный. Эта информация может быть правдивой или ложной. Утверждение может быть расширено так: забор красный или зелёный, цветной и деревянный. Смысл таких высказываний лежит в составных описывающих элементах. Наиболее часто используют три логические операции:
| А | Б | С |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 1 | 1 |
| А | Б | С |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| А | С |
| 0 | 1 |
| 1 | 0 |

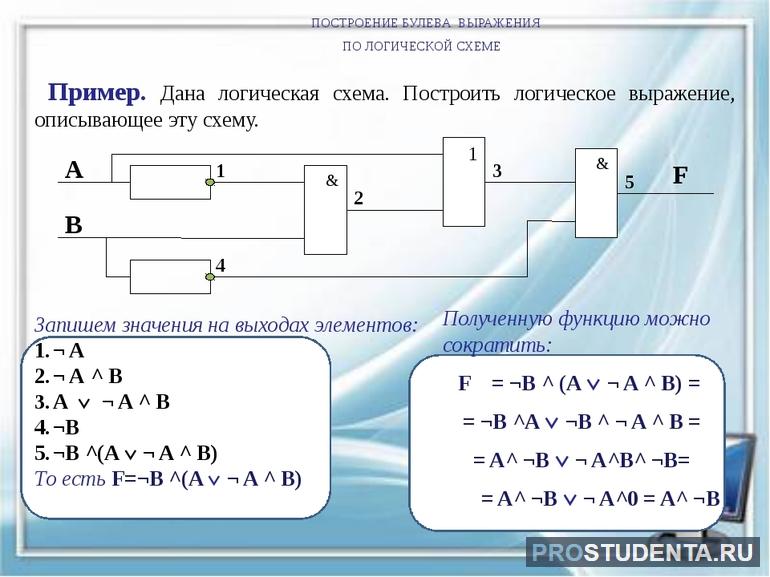
Рассмотренные элементы являются базовыми для построения интегральных микросхем. Как раз их работу и можно пояснить с помощью логических компонентов, вернее, их таблиц истинности. При этом элементы, выполняя определённую функцию (операцию) над входными сигналами (операндами, данными) обеспечивают нужный результат.
Решение задач
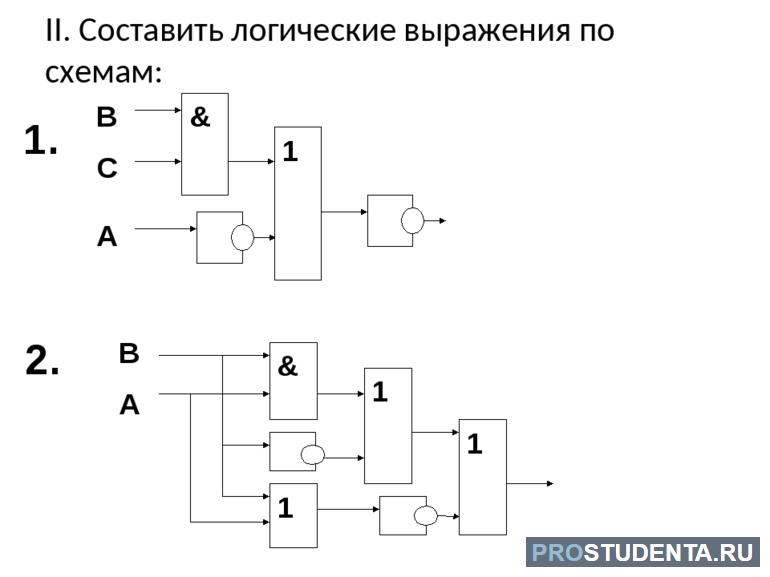
Реальные логические схемы могут содержать тысячи выводов. Их уравнения записывают по так называемой ярусной схеме, условно разделяя устройство на блоки. В общем случае решение задач выполняется по следующей последовательности действий:
- Определяется число входов и выходов элемента.
- Вычерчивается функциональная схема.
- Логическое устройство разбивается на ярусы, которым присваивают номера.
- Подписывают выводы элементов с обозначением названия искомой функции, снабжая её цифровым индексом. Обычно первая цифра — это номер яруса, а оставшиеся — порядковые номера в ярусе.
- Для каждого элемента составляют аналитическое выражение, определяющее его выходную функцию и переменные.
- Выполняют выражение одних выходных функций посредством других, пока не получится булева функция, определяемая входными переменными.
При решении задач используют законы булевой алгебры. Если формулы представляют одну и туже функцию, то их называют равносильными. Эта равнозначность доказывается алгебраическими правилами. Из основных теорем можно выделить: ассоциативность и коммутативность конъюнкции и дизъюнкции, дистрибутивность, идемпотентность. Правила соответствуют сочетательному, переместительному и распределительному законам.
Кроме этого, существуют специальные теоремы:
- двойное отрицание (y = y);
- свойство констант (y * 1 = y; y * 0 = 0; y v 0 = y; 0 = 1; 1 = 0);
- двойственности (y1 * y2 = y1 v y2);
- противоречия (y * y = 0);
- исключения третьего (y v y = 1).
Следует отметить, что существуют и так называемые мажоритарные элементы. Это операнды, имеющие много входов. Например, переменная f на выходе четырёх ходового мажоритарного элемента примет 1, если как минимум три его входа будут соответствовать логической единице.
Формирование у обучающихся навыков применения технологии построения таблиц истинности для составных логических выражений.
Задачи урока:
- Обучающие:
- Научить составлять логические выражения из высказываний
- Сформировать знание о таблицах истинности
- Выработать умение применять последовательность действий построения таблиц истинности
- Научить находить значение логических выражений посредством построения таблиц истинности
- Продолжить развитие умения анализировать
- Продолжить развитие умения устанавливать причинно-следственные связи
- Формировать умения работы с таблицами
- Совершенствовать навыки общения
- Вовлечь в активную деятельность
Вложение Размер Конспект урока 58.01 КБ Презентация к уроку 298.29 КБ Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение – средняя общеобразовательная школа №2 города Аркадака Саратовской области
урока по информатике
Учитель: Дмитриева Елена Матвеевна,
первая квалификационная категория
Дата проведения урока – 16.10.2017.
Тема: Построение таблиц истинности для логических выражений
Тип урока: комбинированный:
- проверка знаний – устная работа;
- новый материал – лекция;
- закрепление – практические упражнения;
- проверка знаний – задания для самостоятельной работы.
Введение понятия Таблица истинности.
Формирование у обучающихся навыков применения технологии построения таблиц истинности для составных логических выражений.
- Обучающие:
- Научить составлять логические выражения из высказываний
- Сформировать знание о таблицах истинности
- Выработать умение применять последовательность действий построения таблиц истинности
- Научить находить значение логических выражений посредством построения таблиц истинности
- Развивающие:
- Продолжить развитие умения анализировать
- Продолжить развитие умения устанавливать причинно-следственные связи
- Формировать умения работы с таблицами
- Воспитательные:
- Совершенствовать навыки общения
- Вовлечь в активную деятельность
- Организационный момент (1 мин).
- Повторение материала предыдущего урока + проверка домашнего задания (устный опрос) (5 мин).
- Объяснение нового материала (10 мин).
- Физкультминутка (1 мин).
- Закрепление
- разбор примера (3 мин);
- практические упражнения (12 мин);
- задания для самостоятельной работы (10 мин).
- Обобщение урока, домашнее задание (3 мин).
Оборудование и программный материал:
- медиапроектор;
- ПК;
- учебник: Информатика 8, Босова Л.Л.
- доска;
- раздаточный справочный материал “Таблицы истинности”;
- демонстрация презентации “Таблицы истинности”.
- Проблемного обучения.
- Личностно-ориентированный подход.
- Здоровьесберегающая.
- ИКТ.
1. Организационный момент
Приветствие, постановка цели и задач урока. Запись в тетради даты и темы урока.
2. Повторение материала предыдущего урока + проверка домашнего задания
3 учащихся работают по карточкам:
Выпишите пары соответствий в первом и втором столбцах:
1. ИСТИНА и ЛОЖЬ
2. Наука о формах и способах мышления
3. Алгебра логики
3. Наука об операциях над высказываниями
4. Значение логической переменной
5. Логическая переменная
5. Повествовательное предложение, содержание которого однозначно может быть истинным или ложным
(1 - 2; 2 - 5; 3 - 3; 4 - 1; 5 - 4)
Остальные ученики отвечают устно:
Вопросы (Слайд №2)
- Что такое высказывание?
- Какие бывают высказывания?
- Приведите пример простого высказывания. Сложного высказывания.
- Как обозначаются высказывания в Алгебре логики?
- Чему могут быть равны логические переменные?
(Слайд №3) Джордж Буль – создатель Алгебры Логики.
3. Объяснение нового материала
На предыдущем уроке вы познакомились с понятиями: высказывание, алгебра логики, логические переменные. А сегодня мы рассмотрим основные логические операции, определённые над высказываниями.
Кстати, что же такое таблица истинности ? Как вы думаете? (Ученики высказывают свои варианты, учитель резюмирует): (Слайд №4)
Таблица истинности – это таблица, показывающая истинность сложного высказывания при всех возможных значениях входящих переменных.
Но для этого запишем в тетради основные логические операции и разберём таблицы истинности для них.
Конъюнкция – логическая операция, ставящая в соответствие двум высказываниям новое высказывание, которое является истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И, ^, *, &.
Конъюнкцию можно описать в виде таблицы истинности: (см. справочный материал)
Конъюнкцию ещё называют логическим умножением.
Существуют несколько связок между простыми высказываниями, но мы рассмотрим ещё две: (Слайд №6)
Дизъюнкция – логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ, ˅, |, +.
Дизъюнкцию можно описать в виде таблицы истинности: (см. справочный материал)
Дизъюнкцию ещё называют логическим сложением.
Инверсия – логическая операция, которая высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ, − , ¬.
Инверсию ещё называют логическим отрицанием.
Назовите логическое значение инверсии для высказывания В.
При построении таблиц истинности есть определенная последовательность действий . Давайте запишем: (Слайд №8)
1. Определить количество строк в таблице:
- количество строк = 2 n +1, где n – количество логических переменных.
2. Определить количество столбцов в таблице:
- количество столбцов = количеству логических переменных + количество логических операций.
3. Построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов ( ¬, &, V);
4. Заполнить столбцы входных переменных наборами значений.
5. Заполнить таблицу истинности, выполняя логические операции в соответствии с приоритетами действий.
Возьмем для примера логическую формулу: ¬(A&B)
и построим таблицу истинности для этого составного высказывания.
Количество строк: 2 2 +1=5, количество столбцов: 2+2=4. Далее заполняем варианты исходных высказываний А В. Теперь заполняем другие столбцы по порядку логических операций.
- Физкультминутка – гимнастика для глаз. (Слайд №9)
Проведём, друзья, сейчас
Упражнение для глаз.
Влево, вправо посмотрели,
Глазки все повеселели.
Снизу вверх и сверху вниз.
Ты, хрусталик не сердись,
Посмотри на потолок,
Отыщи там уголок.
За окно ты посмотри.
Что ты видишь там вдали?
А теперь на кончик носа.
Повтори так 8 раз –
Лучше будет видеть глаз.
Глазки нас благодарят,
Поморгать нам всем велят.
Плавно глазками моргаем,
Потом глазки закрываем.
Чтобы больше было силы,
К ним ладошки приложили.
Раз, два, три, четыре, пять –
Можно глазки открывать!
Потянулись и зевнули,
Спинки дружно все прогнули,
Повернулись вправо, влево
Стало гибким наше тело.
Ножки вытянем вперёд,
Влево, вправо поворот.
Ножки выше поднимаем
И в коленочках сгибаем,
И друг другу улыбнулись.
Головой все повращаем
И урок наш продолжаем.
Разберем следующее упражнение вместе. (Слайд №10) и работа на доске и в тетради.
Учебник: стр. 39 №8 (1, 3)
Количество логических переменных: 2 . Логических операций: 2.
Значит, строк в таблице 2 2 +1=5, столбцов 2+2=4.
Количество логических переменных: 3. Логических операций: 3
Значит, строк в таблице 2 3 +1=9, столбцов 3+3=6.
Задание для самостоятельной работы на готовых карточках. (Слайд №11)
Вам надо заполнить таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
- Обобщение урока, домашнее задание (2 мин). (Слайд №12)
Прошу вас оценить урок, заполнив карточки.
Выпишите пары соответствий в первом и втором столбцах:
1. ИСТИНА и ЛОЖЬ
2. Наука о формах и способах мышления
3. Алгебра логики
3. Наука об операциях над высказываниями
4. Значение логической переменной
5. Логическая переменная
5. Повествовательное предложение, содержание которого однозначно может быть истинным или ложным
1______, 2_______, 3______, 4_______, 5________.
Задание для самостоятельной работы: Постройте таблицу истинности логического выражения
Таблицы истинности для логических выражений
Конъюнкция – логическая операция, ставящая в соответствие двум высказываниям новое высказывание, которое является истинным тогда и только тогда, когда оба исходных высказывания истинны.
Для записи конъюнкции используются следующие знаки: И, ^, *, &.
Конъюнкцию можно описать в виде таблицы истинности: (см. справочный материал)
Конъюнкцию ещё называют логическим умножением.
Дизъюнкция – логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.
Для записи дизъюнкции используются следующие знаки: ИЛИ, ˅, |, +.
Дизъюнкцию можно описать в виде таблицы истинности: (см. справочный материал)
Дизъюнкцию ещё называют логическим сложением.
Инверсия – логическая операция, которая высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.
Для записи инверсии используются следующие знаки: НЕ, − , ¬.
Инверсию ещё называют логическим отрицанием.
Назовите логическое значение инверсии для высказывания В.
Предварительный просмотр:
Подписи к слайдам:
Построение таблиц истинности для логических выражений Урок информатики и ИКТ в 8 Б классе. Подготовила учитель: Дмитриева Е.М. МБОУ-СОШ №2 города Аркадака Саратовской области 16.10.2017
Вопросы : Что такое высказывание? Какие бывают высказывания? Приведите пример простого высказывания. Сложного высказывания. Как обозначаются высказывания в Алгебре логики? Чему могут быть равны логические переменные?
Построение таблиц истинности для логических выражений Таблица истинности – это таблица, показывающая истинность сложного высказывания при всех возможных значениях входящих переменных.
Построение таблиц истинности для логических выражений Конъюнкция – логическая операция, ставящая в соответствие двум высказываниям новое высказывание, которое является истинным тогда и только тогда, когда оба исходных высказывания истинны. Для записи конъюнкции используются следующие знаки: И , ^, *, &. Конъюнкцию ещё называют логическим умножением.
Построение таблиц истинности для логических выражений Дизъюнкция – логическая операция, которая двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны. Для записи дизъюнкции используются следующие знаки: ИЛИ , ˅, |, +. Дизъюнкцию ещё называют логическим сложением.
Построение таблиц истинности для логических выражений Инверсия – логическая операция, которая высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Для записи инверсии используются следующие знаки: НЕ , - , ¬. Инверсию ещё называют логическим отрицанием.
Построение таблиц истинности для логических выражений 1. Определить количество строк в таблице: количество строк = 2 n +1, где n – количество логических переменных. 2. Определить количество столбцов в таблице: количество столбцов = количеству логических переменных + количество логических операций. 3. Построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов ( ¬, &, V ); приоритеты: ( ), ¬, &, V. 4. Заполнить столбцы входных переменных наборами значений. 5. Заполнить таблицу истинности, выполняя логические операции в соответствии с приоритетами действий. ¬( A & B ) Логических переменных: 2 , операций: 2 . Количество строк: 2 2 +1=5 , количество столбцов: 2+2=4.
Построение таблиц истинности для логических выражений У чебник: стр. 39 №8 (1, 3 ) Постройте таблицы истинности для следующих логических выражений: 1) В &(АVВ) 3) А &( A˅B˅C)
Построение таблиц истинности для логических выражений. Самостоятельная работа А В С ¬ C A&B A&B˅¬C ¬(A&B˅¬C)
Построение таблиц истинности для логических выражений. Ответ: А В С ¬ C A&B A&B˅¬C ¬(A&B˅¬C) 0 0 0 1 0 1 0 0 0 1 0 0 0 1 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 0 0 1 0 1 0 1 0 1 0 0 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 3 4 5
Спасибо за урок! Прошу вас оценить урок, заполнив карточки. Оценки за ответы.
По теме: методические разработки, презентации и конспекты
![]()
Логические выражения и базовые логические операции. Таблицы истинности.
В данной разработке приведены план-конспект урока по теме: "Логические выражения и базовые логические операции. Таблицы истинности". Презентация с дополнительными файлами позволяет сэкономить вр.
![]()
Алгебра высказываний. Таблицы истинности основных логических операций
Класс: 9-11 классТема: Алгебра высказываний. Таблицы истинности основных логических операцийТип урока: урок изучения нового материалаПродолжительность занятия: 45 минут.
Построение таблиц истинности для логических выражений.
Построение таблиц истинности для логических выражений конспект урока.
Построение таблиц истинности для логических выражений
УРОК ИНФОРМАТИКИ ПО ТЕМЕ.
Информатика "Построение таблиц истинности для логических выражений" 8 класс
Урок построен на основе модульных технологийНа уроке у учащихся появится возможность научиться строить таблицу истинности для логических выражений.На уроке учащиеся:анализируют последовательность.
Решение логических задач ЕГЭ Построение таблиц истинности логических выражений
Решение логических задач ЕГЭПостроение таблиц истинности логических выражений.
![]()
Урок по информатике 8 класс. Тема: "Построение таблиц истинности для логических выражений"
Тема урока: Построение таблиц истинности для логических выраженийТип урока: комбинированный:проверка знаний – устная работа;новый материал – лекция;закрепление – практическ.
Формирование у обучающихся навыков применения технологии построения таблиц истинности для составных логических выражений.
Научить составлять логические выражения из высказываний
Углубить знание о таблицах истинности
Выработать умение применять последовательность действий построения таблиц истинности
Научить находить значение логических выражений посредством построения таблиц истинности
Продолжить развитие умения анализировать
Продолжить развитие умения устанавливать причинно-следственные связи
Формировать умения работы с таблицами
Совершенствовать навыки общения
Вовлечь в активную деятельность
Повторение материала предыдущего урока + проверка домашнего задания (устный опрос)
Объяснение нового материала
задания для самостоятельной работы.
Обобщение урока, домашнее задание.
1. Организационный момент
Проверка отсутствующих в классе
2. Повторение материала предыдущего урока + проверка домашнего задания
На прошлом уроке мы познакомились с таким понятием как Алгебра логики.
2 слайд. Давайте вспомним, что такое логика и кто же ее основоположники?
(Аристотель, Джордж Буль, Клод Шеннон)
3 слайд. А что такое алгебра? (Алгебра - наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над разнообразными математическими объектами – числами, многочленами, векторами и др)
4 слайд. Что такое высказывание? (Высказывание – это повествовательное предложение, содержание которого можно однозначно определить как истинное или ложное)
Молодцы! Посмотрите на следующие предложения и скажите, являются ли они высказыванием?
5 слайд. Мы с вами знаем, что высказывания бываю простые и сложные. Сложные высказывания строятся из простых при помощи логических операций и", "или", "не", "если … то", "тогда и только тогда" и др.
Слайд 6. В следующих высказываниях выделите простые, обозначив каждое из них буквой:
Зимой дети катаются на коньках или на лыжах
A = Зимой дети катаются на коньках
B = Зимой дети катаются на лыжах
Неверно, что Солнце движется вокруг Земли
A = Солнце движется вокруг Земли
Мы увидели, что логика достаточно крепко связана с нашей повседневной жизнью, а также увидели, что почти любое высказывание можно записать в виде логического выражения – формулы.
8 слайд. Давайте вспомним:
Когда инверсия истинна и когда инверсия ложна?
В каком случае дизъюнкция ложна?
В каком случае конъюнкция истинна?
3. Объяснение нового материала
9 слайд На предыдущем уроке вы находили значение составного высказывания путем подстановки исходных значений входящих логических переменных. А сегодня мы узнаем, как можно построить таблицу истинности, которая определяет истинность или ложность логического высказывания при всех возможных комбинациях исходных значений простых высказываний (логических переменных).
Кстати, что же такое таблица истинности? Как вы думаете? (Ученики высказывают свои варианты, учитель резюмирует):
Таблица истинности – это таблица, показывающая истинность сложного высказывания при всех возможных значениях входящих переменных.
Возьмем для примера логическую формулу: А˅А^В
и построим таблицу истинности для этого составного высказывания.
При построении таблиц истинности есть определенная последовательность действий. Давайте запишем: (Слайд №10)
1. Определить количество строк в таблице:
количество строк = 2n+1, где n – количество логических переменных.
2. Определить количество столбцов в таблице:
количество столбцов = количеству логических переменных + количество логических операций.
3. Построить таблицу истинности с указанным количеством строк и столбцов, ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов (¬, &, V);
приоритеты: ( ), ¬, &, V.
4. Заполнить столбцы входных переменных наборами значений.
5. Заполнить таблицу истинности, выполняя логические операции в соответствии с приоритетами действий.
Количество строк: 22+1=5, количество столбцов: 2+2=4. Далее заполняем варианты исходных высказываний А В. Теперь заполняем другие столбцы по порядку логических операций. (Слайд №4)
Читайте также:





