Как сделать сумматор
Мы уже знакомы с двоичным исчислением и базовыми логическими элементами.
Предлагаю продолжить знакомство и сейчас начнем моделировать сумматор двоичных чисел.
Задача: собрать сумматор двоичных чисел.
Опять вопрос: с чего же начать. Как всегда моделируем работу на базе одного разряда, составляем таблицу переходов и вперед.
Заполняем правую часть. всего 4 строчки на 2 столбца. Попробуйте самостоятельно это сделать, а потом продолжить чтение.
Что получилось: если 0 сложить с нолем, логично, что получится ноль, аналогично просто ноль плюс один будет один. Продолжаем, далее. один плюс один будет ноль и "один в уме".
Итак, есть таблица по которой видно, что S=1 Если А=0 и одновременно В=1 или В=0 и одновременно А=1 , Логическим выражением можно записать так S=(НЕ А)*В +(НЕ В)*А.
Теперь со знаком переноса, С=1 при условии, что А=1 и одновременно В=1. Можно записать так С=А*В. Теперь Вам задача: нарисовать схему на логических элементах в соответствие с таблицей и формулами. Проверяется она простым перебором входов и просчетов выходов.
Заметим сразу, что схема этого устройства в том виде, в котором мы ее сейчас будем конструировать, сама по себе довольно бесполезна — если вы, конечно, не хотите повторить подвиг советского конструктора Михаила Александровича Карцева. Он создал в 1970-х годах на микросхемах малой степени интеграции (то есть фактически на отдельных логических элементах) очень удачную ЭВМ под названием М-10, отличившуюся тем, что отдельные ее экземпляры в нашем оборонном комплексе, по слухам, продержались аж до начала нового тысячелетия. При желании повторить такой подвиг, учтите, что основная проблема, которую вам придется решать, состоит вовсе не в том, чтобы такую машину сконструировать схемотехнически — это не самая трудная часть работы. Самое трудное для подобных суперконструкций — решить проблему отвода тепла, выделяемого сотнями тысяч быстродействующих логических микросхем. Суперкомпьютеры Cray на дискретных элементах, выпускаемые в 1980-х годах, даже имели водяное охлаждение.
Наконец, если очень хочется, то готовый двоичный сумматор есть в интегральном исполнении (561ИМ1; есть сумматоры и помощнее). Зачем же мы тогда будем его конструировать? А затем, что его устройство очень хорошо иллюстрирует две вещи: во-первых, само применение логических микросхем, во-вторых— разве не любопытно знать, как устроен самый главный узел компьютера, арифметико-логическое устройство, АЛУ? Знание этого вам очень пригодится для лучшего понимания работы микроконтроллеров и принципов их пррграммирования. Кроме того, мы на этом примере познакомимся еще с одним важным типом логических элементов.
Итак, вспомним, что нам, собственно, нужно делать — а именно воспроизвести таблицу сложения двоичных чисел, которая была показана для одноразрядных чисел в предыдущей главе. Так как при сложении единиц получается двухразрядное число, то перепишем эту таблицу в двухразрядном представлении:
Теперь разобьем таблицу на две: одну для разряда собственно суммы, другую для значения переноса в следующий разряд:
Сравним вторую таблицу с таблицей состояний для базовых логических функций (я их повторю, чтобы не приходилось листать книгу):
Рис. 15.6. Схема одноразрядного полусумматора
Рис. 15.7. Схема многоразрядного сумматора
Так мы получили одноразрядный полный сумматор. Объединением таких сумматоров несложно соорудить устройство для сложения чисел любой разрядности. Если вы попробуете разрисовать схему сумматора для, скажем, восьми разрядов полностью, с использованием принципиальных схем логических элементов по рис. 15.1, то ужаснетесь — это же сколько транзисторов надо, чтобы построить такое устройство? Много — в восьмибитном КМОП-сумматоре их получается 480 штук (а современные микросхемы, бывает, содержат и больше транзисторов). И это без учета того, что в систему должны входить еще, как минимум, два регистра для хранения исходных чисел и результата (в целях экономии результат помещают в регистр одного из слагаемых, тем самым слагаемое это уничтожая), а также другие логические схемы (для сдвига, для инверсии битов при манипуляции с отрицательными числами). То есть общее количество транзисторов составляет порядка тысячи.
Теперь понятно, почему микросхемы высокой степени интеграции содержат миллионы транзисторов и почему проблема отвода тепла стоит так остро! Один логический элемент КМОП из четырех транзисторов, согласно рис. 15.2, выделяет при частоте в единицы мегагерц всего-навсего пол милливатта тепла, но что будет, если таких элементов приходится ставить в количестве миллион штук? И еще при этом как можно сильнее повышать рабочую частоту?
Предположим, мы имеем такой байтовый сумматор и под числами имеем в виду обычные беззнаковые положительные числа, диапазон которых составит 0—255. Если мы сложим 128 (1000 0000) и 128 (1000 0000), то получим число 256 (1 0000 0000), которое имеет единицу в 9-м, отсутствующем у нас разряде (заодно отметим этот результат как хорошую иллюстрацию к положению, гласящему, что умножение на 2 есть просто сдвиг всех разрядов влево). Таким образом, в разрядах сумматора мы получаем просто О, что, конечно, есть результат некорректный, для корректного сложения, к примеру, восьмибитовых чисел нам надо иметь 9 разрядов результата.
В этой главе давайте поговорим об основных арифметических схемах, таких как двоичный сумматор и двоичный вычитатель. Эти схемы могут работать с двоичными значениями 0 и 1.
Двоичный сумматор
Самая основная арифметическая операция — сложение. Схема, которая выполняет сложение двух двоичных чисел, называется двоичным сумматором . Во-первых, давайте реализуем сумматор, который выполняет сложение двух битов.
Полумесяц
Половина сумматора представляет собой комбинационную схему, которая выполняет сложение двух двоичных чисел A и B, состоящих из одного бита . Он выдает две выходные суммы, S & carry, C.
Таблица истинности Half сумматора показана ниже.
| входные | Выходы | ||
|---|---|---|---|
| В | С | S | |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Когда мы добавляем два бита, результирующая сумма может иметь значения в диапазоне от 0 до 2 в десятичном виде. Мы можем представить десятичные цифры 0 и 1 одним битом в двоичном виде. Но мы не можем представить десятичную цифру 2 с одним битом в двоичном виде. Итак, нам требуется два бита для представления его в двоичном виде.
Пусть, sum, S — младший значащий бит и перенос, C — старший значащий бит полученной суммы. Для первых трех комбинаций входов, carry, C равен нулю, а значение S будет равно нулю или единице в зависимости от количества единиц, присутствующих на входах. Но, для последней комбинации входных данных, carry, C равен единице, а sum равен нулю, поскольку результирующая сумма равна двум.
Из таблицы Truth мы можем напрямую записать логические функции для каждого вывода как
S = A o p l u s B
Мы можем реализовать вышеуказанные функции с 2-входным вентилем Ex-OR и 2-входным вентилем AND. Принципиальная электрическая схема полумесяца показана на следующем рисунке.
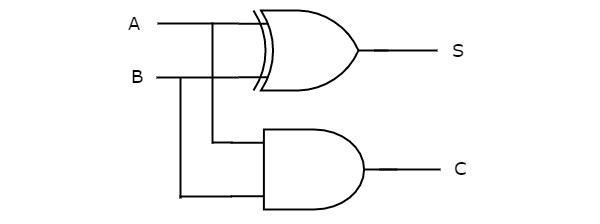
В приведенной выше схеме два входных логических элемента ИЛИ-И и два входных И логических элемента И дают сумму, S и перенос, C соответственно. Следовательно, Half-сумматор выполняет сложение двух битов.
Полный сумматор
Полный сумматор представляет собой комбинационную схему, которая выполняет сложение трех битов A, B и C в . Где A & B — два параллельных значащих бита, а C in — бит переноса, который генерируется из предыдущего этапа. Этот полный сумматор также выдает две выходные суммы, S & carry, C out , которые аналогичны полумесяцу.
Таблица истинности полного сумматора показана ниже.
| входные | Выходы | |||
|---|---|---|---|---|
| В | С в | C out | S | |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Когда мы добавляем три бита, результирующая сумма может иметь значения в диапазоне от 0 до 3 в десятичном виде. Мы можем представить десятичные цифры 0 и 1 одним битом в двоичном виде. Но мы не можем представлять десятичные цифры 2 и 3 одним битом в двоичном виде. Итак, нам требуется два бита для представления этих двух десятичных цифр в двоичном виде.
Пусть, sum, S — младший значащий бит и перенос, C out — старший значащий бит из результирующей суммы. Легко заполнить значения выходов для всех комбинаций входов в таблице истинности. Просто посчитайте количество единиц на входах и запишите эквивалентное двоичное число на выходах. Если C in равен нулю, то полная таблица истинности сумматора такая же, как в таблице истинной половины сумматора.
Мы получим следующие логические функции для каждого вывода после упрощения.
S = A o p l u s B o p l u s C i n
c o u t = A B + l e f t ( A o p l u s B r i g h t ) c i n
Сумма S равна единице, когда на входах присутствует нечетное число единиц. Мы знаем, что вентиль Ex-OR производит вывод, который является нечетной функцией. Таким образом, мы можем использовать либо два входа Ex-OR с 2 входами, либо один вентиль Ex-OR с 3 входами, чтобы получить сумму S. Мы можем реализовать перенос C , используя два вентиля И с двумя входами И и один вентиль ИЛИ. Принципиальная электрическая схема полного сумматора показана на следующем рисунке.
При отсутствии телевизионной антенны коллективного пользования, особенно в сельской местности, часто возникает необходимость установкидвух или нескольких раздельных антенн.
Это может быть связано с необходимостью использования узкополосных одноканальных антенн для приема разных программ от одного и того же телецентра или ретранслятора, когда требуются антенны с большим коэффициентом усиления. В других случаях необходимо принимать разные программы от телевизионных передатчиков, расположенных в разных направлениях, а каждый раз заниматься поворотом антенны вручную или конструировать специальное поворотное устройство нежелательно.
В таких условиях обычно от каждой антенны спускается отдельный фидер, что нецелесообразно, так как при переходе с приема одной программы на другую приходится переставлять штекеры фидеров в антенное гнездо телевизора. Установка переключателя фидеров у телевизора также не решает проблемы: не устраняется большой расход дорогостоящего кабеля, а при слабом сигнале для компенсации затухания сигнала в фидерах пришлось бы у каждой антенны устанавливать .отдельный антенный усилитель.
Эти проблемы могут быть решены исключительно путем объединения сигналов, принятых антеннами, с канализацией их к телевизору по одному общему фидеру. Однако, непосредственно соединять между собой разные антенны невозможно в связи с тем, что нарушится их согласование с фидерами: сигнал, принятый одной антенной, будет разветвляться и лишь частично поступать в фидер.
Другая антенна, подключенная параллельно фидеру, может представлять собой такую нагрузку, что уровень сигнала от первой антенны, поступающий в фидер, окажется недопустимо малым. Поэтому необходимо, специальное устройство для сложения сигналов, которое не нарушало бы согласования антенн.
На рис. 1 показана схема фильтра сложения сигналов (ФСС) метрового диапазона. Назначение фильтра состоит в том, чтобы сигнал, принятый антенной 1, полностью поступил в фидер и не ответвлялся в цепь антенны 2, а сигнал, принятый антенной 2, также полностью поступил в фидер и не ответвлялся в цепь антенны 1.

Рис. 1. ФСС с использованием ФНЧ и ФВЧ.
Эта задача реализуется использованием двух фильтров. Фильтр, образованный элементами LI, Cl, L2, С2 и С5, представляет собой фильтр нижних частот (ФНЧ), а фильтр, образованный элементами L3, С3, L4, С4 и L5, - фильтр верхних частот (ФВЧ). Если антенна 1 рассчитана на прием сигнала с меньшим номером,канала, то есть с меньшей частотой, чем антенна 2, то сигнал от антенны 1 свободно проходит . через ФНЧ и поступает в фидер, не ответвляясь в цепь антенны 2, так как ФВЧ представляет для него большое сопротивление.
Аналогично, сигнал, принятый антенной 2, беспрепятственно проходит через ФВЧ и поступает в фидер, а ФНЧ, имеющий для этого сигнала большое сопротивление, не пропускает pro к антенне 1. Во избежание отражения сигналов, принятых антеннами, от ФСС характеристические сопротивления обоих фильтров должны приблизительно составлять 75 Ом.
Катушки индуктивности фильтра наматываются проводом ПЭВ-2 диаметром 0,6 мм виток к витку на каркасах из полистирола или оргстекла: диаметром 5 мм. Катушки L1. L4 располагаются на одном общем каркасе, расстояния между катушками должны быть не менее ,8 мм. Катушка L5 наматывается на отдельном каркасе и конструктивно размещается так, чтобы ее ось была перпендикулярна оси других катушек. Количество витков катушек и емкости конденсаторов для разных комбинаций каналов приведены в таблице 1.
Таблица 1. Данные для катушек и конденсаторов.
| Номер канала антенны | Количество витков катушек | Емкость, пФ | |||||
| 1 | 2 | L1, L2 | L3, L4' | L5 | С1,С2 | С3, С4 | С5 |
| 1-5 | 6-12 | 2 | 11 | 3 | 12 | 12 | 20 |
| 1 | 3 | 3,5 | 8,5 | 6 | 47 | 39 | 33 |
| 1 | 4 | 3,5 | 7 | 5 | 47 | 36 | 33 |
| 1 | 5 | 3,5 | 5 | 6 | 47 | 43 | 33 |
| 2 | 3 | 3,5 | 8,5 | 6 | 47 | 39 | 30 |
| 2 | 4 | 3 | 7 | 5 | 47 | 36 | 30 |
| 2 | 5 | 3 | 5 | 6 | 43 | 43 | 30 |
| 3 | 5 | 2,5 | 5 | 6 | 33 | 43 | 30 |
Рассмотренный вариант ФСС компактен и дешев в изготовлении, но страдает одним недостатком: в любительских условиях невозможно учесть паразитные емкости монтажа и индуктивности выводов катушек, конденсаторов и соединительных проводов, которые на частоте десятков и сотен Мегагерц оказывают существенное влияние на работу.
Поэтому добиться паспортных значений ослабления сигнала не более, чем на 1 дБ и развязки между антеннами не менее, чем на 15 дБ в любительских условиях трудно. По этой причине нельзя предложить ФСС по этой схеме, который позволил бы подключить к общему фидеру две антенны, работающие в диапазоне 6-12 каналов.

Рис. 2. Способ намотки катушек.
Более широкими возможностями обладает ФСС, схема которого показана на рис. 3. Он собран из шести отрезков коаксиального кабеля той же марки, что и фидеры.

Рис. 3. ФСС из отрезков кабеля.
Работа этого фильтра основана на трех важнейших выводах теории длинных линий:
Фильтр рассчитан на подключение двух антенн: антенны с меньшим-номером канала - ’’а” и антенны с большим номером канала - "б". Размеры отрезков кабеля выбираются следующим образом. Длина отрезка 2 равна половине длины волны в кабеле для канала "б", длина отрезка 3 - четверти длины волны в кабеле для канала ”6”, длина отрезка 4 - четверти длины-волны в кабеле для канала "а”, а длина отрезка 6 - половине длины волны в, кабеле для канала "а".
Длина,отрезков 1 и 5 выбирается так, чтобы суммарная длина отрезков 1 и 2 составляла половину длины волны в кабеле для канала1 "а”, а суммарная длина отрезков 5 и 6 - несколько полуволн в кабеле для ! канала "б".
Рассмотрим прохождение сигнала от антенны канала "а". Поступая по фидеру к точке соединения отрезков 1 и 2, сигнал свободно проходит через отрезок 3 и далее в фидер к телевизору, так как отрезки 1 и 2 в сумме имеют длину в полволны для этого канала, и их сопротивление бесконечно велико.
Сигнал не ответвляется в отрезок 4. в связи с тем, что отрезок 6 для него равен половине длины волны и замыкает накоротко конец отрезка 4, а длина этого отрезка составляет четверть длины волны для канала "а", так что входное сопротивление отрезка 4 бесконечно велико.
Аналогично проходит сигнал от антенны канала "б" с тем лишь различием, что в сумме длина отрезков 5 и 6 равна нескольким половинам длины волны для канала "б". Размеры отрезков, 2, 3, 4 и 6 для разных каналов сведены в табл. 2, а размеры отрезков 1 и 5 - в табл. 3. Здесь выше диагонали приводятся размеры В, а ниже диагонали - Г.
Таблица 2. Размеры отрезков, 2, 3, 4 и 6 для разных каналов.
| Номер канала | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | И | 12 |
| А | 933 | 791 | 613 | 558 | 512 | 276 | 265 | 254 | 244 | 234 | 226 | 218 , |
| 2А | 1865 | 1581 | 1227 | 1116 | 1023 | 553 | 529 | 508 | 487 | 469 | 452 | 436 |

Приведем пример определения элементов фильтра для подключения антенны 2-го канала и антенны 7-го канала к общему фидеру. Тогда индекс ”а” соответствует каналу 2, а индекс ”б” - каналу 7. Из табл. 8.2 находим размеры отрезков: 2 - 529 мм, 3 - 265 мм, 4 - 791 мм, 6 - 1581 мм. Из табл.
3 в строке для канала 2 и столбце для канала 7 находим длину отрезка 1 (В) - 1052 мм, а в строке для канала 7 и столбце для канала 2 -длину отрезка 5 (Г) - 535 мм.
Из табл. 3 видно, что в диапазоне 6-12 каналов антенны соседних каналов соединять с помощью ФСС нельзя, но и в тех случаях, когда номера каналов отличаются на 2, длина некоторых отрезков оказывается малой, меньше 50 мм, а такой фильтр будет работать хуже обычного, так как погрешность длины отрезка составит значительный процент от его длины.
По этой же причине не удается создать ФСС для дециметровых каналов или для сочетания метрового и дециметрового каналов. В этих случаях проблема может быть решена коммутацией антенн с помощью электромагнитного реле.
Рис. 4. Схема коммутации антенн.
На рис. 4 показана схема такой коммутации двух антенн на один общий фидер. При этом реле располагается на мачте поблизости от антенн и управляется дистанционно от телевизора с помощью тумблера. Питание реле осуществляется от источника питания телевизора и подается по фидеру.
Резистор R предназначен для гашения излишнего напряжения, а конденсаторы препятствуют замыканию постоянного напряжения питания реле антеннами и входной цепью телевизора, пропуская без потерь высокочастотный сигнал. В схеме используется электромагнитное реле РЭС15 паспорт РС4.591.001П2 или РС4.591.008П2. Можно также использовать реле РЭС10 паспорт РС4.524.301П2 или РС4.524.313П2, но при этом сопротивление резистора R необходимо уменьшить до 6,8 кОм.
Используя схему коммутации, можно подключать к общему фидеру две раздельные дециметровые антенны или метровую и дециметровую антенны. Если же совместить схему коммутации с ФСС, можно подключить к общему фидеру три или четыре метровые антенны, а также две метровые и одну дециметровую антенны. При этом пара антенн подключается к входам ФСС, а выход ФСС - к схеме коммутации.
Никитин В.А., Соколов Б.Б., Щербаков В.Б. - 100 и одна конструкция антенн.
Читайте также:


