Как сделать смежный угол
Всем привет! Сегодня решил поговорить о геометрии и начать хочется с одной из первых тем 7 класса - смежные и вертикальные углы.
Смежные углы
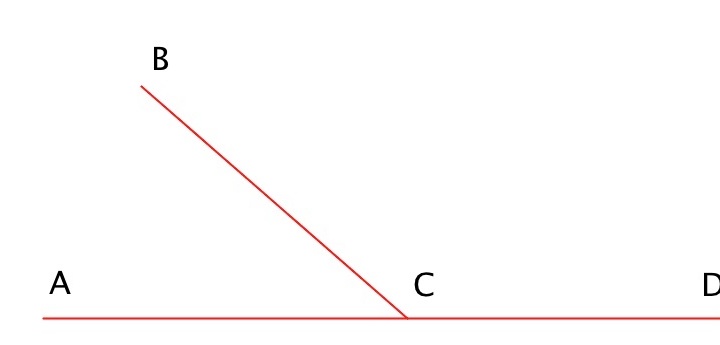
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Здесь смежными углы это DOA и DOC (сторона DO общая, АО продолжение ОС и наоборот), COB и AOB (сторона ВО общая, АО продолжение ОС и наоборот).
Теперь об особенностях.
Значит, DOA + DOC и COB + AOB = 180 градусов.
Теперь о вертикальных углах.
Вертикальные углы
Если говорить простым языком, то по сути это два угла в виде "крест на крест".
На этом рисунке углы DOA и COB, DOC и AOB - вертикальные, поскольку OC является продолжением AO, а OB продолжением DO.
То есть DOA = COB, DOC = AOB.
Эти две теоремы нужно запомнить, чтобы решать задачи по геометрии и номер 19 из первой части ОГЭ.
Теории не очень много, поэтому эту тему можно назвать простой. Но в любой теме важна практика, так что давайте решать задачи.
Практика
1. Смежные углы относятся как 4:5. Найдите эти углы.
1) Нам известно, что сумма любых смежных углов 180 градусов.
Возьмем градусы в одной части за "икс" и составим уравнение.
4х + 5х = 180
9х = 180 х = 180 /9
х = 20
Теперь найдем углы, умножив значение "иск" на число частей угла.
2) 4х = 4 · 20 = 80 градусов 5х = 5 · 20 = 100 градусов
Ответ: Углы равны 80 и 100 градусов.
2. Найдите величину каждого из двух вертикальных углов, если их сумма равна 30 градусов.
Вертикальные углы равны, следовательно их сумму нужно разделить пополам, на 2.
30 / 2 = 15 градусов.
Ответ: 15 градусов
3. Один из смежных углов в 8 раз больше другого. Найдите оба угла.
1) Сумма смежных углов 180 градусов, зная это мы можем составить уравнение, обозначив за "икс" меньший угол.
8х + х = 180
9х =180
х = 180 / 9
х = 20
2) 8 · х = 8 · 20 = 160 градусов
Ответ: углы равны 20 и 160 градусов.
Домашка
Без нее никак)
1) Смежные углы относятся как 2:4. Найдите эти углы.
2) Один из смежных углов в 6 раз больше другого. Найдите оба угла.
3) Найдите величину каждого из двух вертикальных углов, если их сумма равна 20 градусов.
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развёрнутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны (только в том случае, когда смежные углы не равны).

∠ABD и ∠DBC — это смежные углы, AC — прямая, луч BD — общая сторона углов и наклонная к прямой AC, ∠ABC — развёрнутый угол, B — основание наклонной.
Чтобы построить угол, смежный с данным углом, нужно одну из сторон угла продлить за вершину:

Сумма смежных углов
Любые два смежных угла составляют в сумме развёрнутый угол. Развёрнутый угол равен двум прямым углам, поэтому можно сказать, что сумма двух смежных углов равна двум прямым углам.

∠ABD + ∠DBC = 2d,
где d — это обозначение прямого угла (d = 90°).
Вертикальные углы
Вертикальные углы — это пара углов, у которых стороны одного угла являются продолжением сторон другого угла. Пересечение двух прямых линий образует две пары вертикальных углов:

∠AOB и ∠COD, а также ∠AOD и ∠BOC — вертикальные углы.
Равенство вертикальных углов
Вертикальные углы равны между собой. Рассмотрим вертикальные углы 1 и 3:

Сумма ∠1 и ∠2 равна развёрнутому углу (180°). Сумма ∠2 и ∠3 тоже равна развёрнутому углу (180°). Значит:
∠1 + ∠2 = ∠2 + ∠3
Следовательно, ∠1 = ∠3. Равенство вертикальных углов доказано.
Смежные углы — это два угла, у которых есть общая вершина и одна сторона, а две другие стороны являются продолжением друг друга и лежат на одной прямой.
Свойства и виды смежных углов в геометрии
- Так как две стороны смежных углов образуют прямую линию, то вместе они составляют развернутый угол. Его градусная мера составляет 180^\circ. Следовательно — сумма смежных углов тоже равна \(180^\circ.\)
- Если две прямые пересекаются, то они образуют две пары смежных углов: \(\angle1\) и \(\angle2\) , \(\angle3\) и \(\angle4\) , а также \(\angle1\) и \(\angle3\) , \( \angle2\) и \(\angle4\) . При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.
- У смежных углов одинаковые синусы.
- Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
- Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.
В паре, если один угол тупой, то по правилу другой обязательно острый.
Если один из углов является прямым, то второй тоже прямой.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти, чему равна сумма
Сумма смежных углов всегда составляет 180 градусов.
Отсюда следует формула:
Примеры решения задач
Задача №1
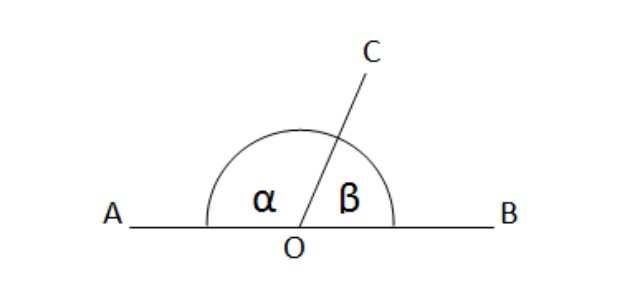
Дано: \(\angle\alpha\) и \(\angle\beta\) — смежные, \(\angle\beta=60^\circ\) .
Найти: чему равен \(\angle\alpha\) .
Решение
Так как углы смежные, значит:
Ответ: \(\;\angle\alpha=120^\circ\) .
Задача №2
Дано: \( \angle\alpha\) и \(\angle\beta\) — смежные, \(\angle\alpha\) на \(30^\circ\) больше, чем \(\angle\beta.\)
Найти: чему равны \(\angle\alpha\) и \(\angle\beta.\)
Решение
Допустим, \( \angle\beta=x\) , тогда \(\angle\alpha=x+30^\circ.\)
Так как сумма смежных углов равна 180 градусов, то получаем уравнение, которое выглядит, как:
Значит, величина \(\angle\beta=75^\circ.\)
Чтобы найти \(\angle\alpha\) , нужно выполнить стандартные вычисления согласно теореме о сумме:
Угол – это геометрическая фигура ( рис.1 ), образованная двумя лучами OA и OB ( стороны угла ), исходящими из одной точки O ( вершина угла ).
СМЕЖНЫЕ УГЛЫ — два угла, сумма которых равна 180°. Каждый из этих углов дополняет другой до развернутого угла.

Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через.
Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными полупрямыми.
На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые.
На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C.
Теорема о смежных углах
Теорема: сумма смежных углов равна 180°
Доказательство:
Углы a1b и a2b смежные (см. рис. 2) Луч b проходит между сторонами a1, и a2 развернутого угла. Следовательно, сумма углов a1b и a2b равна развернутому углу, то есть 180°. Теорема доказана.
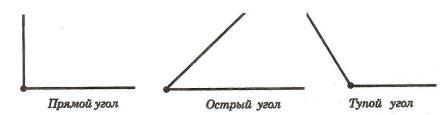
Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол.
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Определение 1. Углом называется часть плоскости, ограниченная двумя лучами с общим началом.
Определение 1.1. Углом называют фигуру, состоящую из точки - вершины угла - и двух различных полупрямых, исходящих из этой точки, - сторон угла.
Например, угол ВОС на рис1 Рассмотрим сначала две пересекающиеся прямые. При пересечении прямые образуют углы. Есть частные случаи:
Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым.
Определение 3. Прямой угол - это угол величиной в 90 градусов.
Определение 4. Угол, меньший 90 градусов, называется острым углом.
Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом.
пересекающиеся прямые.
Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными.
Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
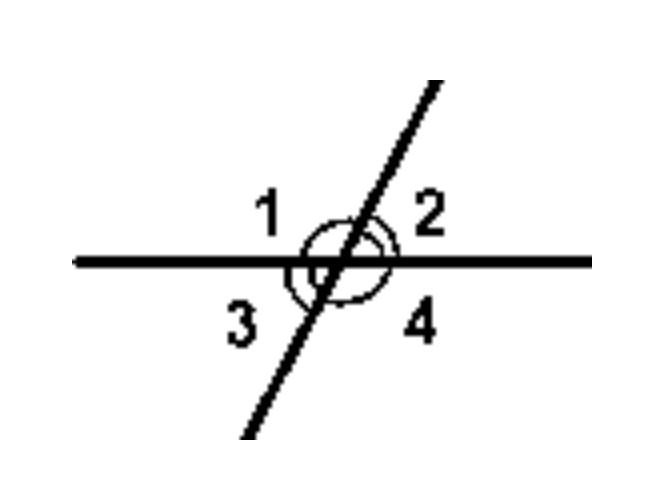
На рисунке 1:
смежные: 1 и 2; 2 и 3; 3 и 4; 4 и 1
вертикальные: 1 и 3; 2 и 4
Теорема 1. Сумма смежных углов равна 180 градусов.
Для доказательства рассмотрим на рис. 4 смежные углы АОВ и ВОС. Их суммой является развернутый угол АОС. Поэтому сумма данных смежных углов равна 180 градусов.

Интересный факт
Связь математики с музыкой
"Раздумывая об искусстве и науке, об их взаимных связях и противоречиях, я пришел к выводу, что математика и музыка находятся на крайних полюсах человеческого духа, что этими двумя антиподами ограничивается и определяется вся творческая духовная деятельность человека и, что между ними размещается все, что человечество создало в области науки и искусства."
Г. Нейгауз
Казалось бы, искусство - весьма отвлеченная от математики область. Однако связь математики и музыки обусловлена как исторически, так и внутренне, несмотря на то, что математика - самая абстрактная из наук, а музыка - наиболее отвлеченный вид искусства.
Консонанс определяет приятное для слуха звучание струны
В основе этой музыкальной системы были два закона, которые носят имена двух великих ученых - Пифагора и Архита. Вот эти законы:
1. Две звучащие струны определяют консонанс, если их длины относятся как целые числа, образующие треугольное число 10=1+2+3+4, т.е. как 1:2, 2:3, 3:4. Причем, чем меньше число n в отношении n:(n+1) (n=1,2,3), тем созвучнее получающийся интервал.
2. Частота колебания w звучащей струны обратно пропорциональна ее длине l .
w = a : l ,
где а - коэффициент, характеризующий физические свойства струны.
Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
Геометрия вокруг нас
Геометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке.
1. Вот на столе на книжной подставке стоит книга. Какой угол она образует?
2. А вот ученик работает за ноутбуком. Какой угол вы видите здесь?
3. Какой угол образует фото рамка на подставке?
4. Как вы думаете, возможно ли, чтобы два смежных угла были равными?
Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре.
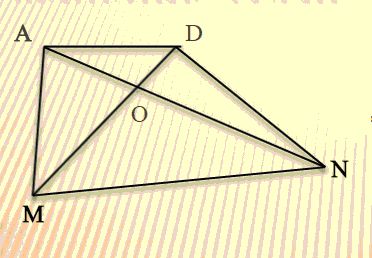
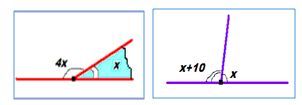
Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке.

Решение задач
Математический диктант на повторение ранее выученного материала
Решите задачи:
1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°?
2. На рисунке найдите все пары смежных углов. А теперь вертикальных углов. Назовите эти углы.
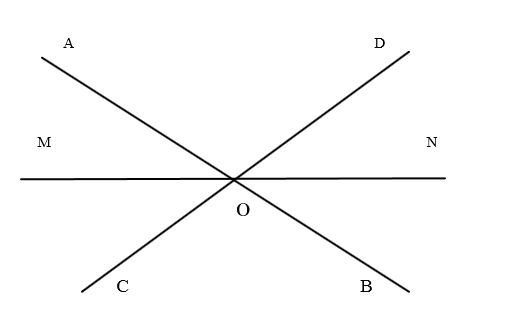
3. Нужно найти угол, когда он втрое больше, чем смежный с ним.
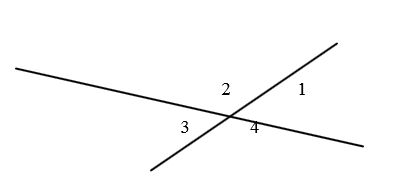
4. Две прямые пересеклись между собой. В результате этого пересечения образовались четыре угла. Определите величину любого из них, при условии что:
а) сумма 2-х углов из четырех 84°;
б) разность 2-х углов из них равна 45°;
в) один угол в 4 раза меньше чем второй;
г) сумма трех из данных углов равна 290°.
Итог урока
1. назовите углы, которые образуются при пересечении 2-х прямых?
2. Назовите все возможные пары углов, находящихся на рисунке, и определите их вид.
Домашнее задание:
1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго.
2. Найдите углы, которые образуются при пересечении 2-х прямых, при условии, что один из углов равняется сумме 2-х других углов, смежных с ним.
3. Необходимо найти смежные углы, когда биссектриса одного из них образует со стороной второго угол, который больше чем второй угол на 60°.
4. Разница 2-х смежных углов равна трети от суммы этих двух углов. Определите величины 2-х смежных углов.
5. Разница и сумма 2-х смежных углов относятся как 1 : 5 соответственно. Найдите смежные углы.
6. Разница двух смежных составляет 25% от их суммы. Как относятся величины 2-х смежных углов? Определите величины 2-х смежных углов.
Читайте также:


