Как сделать схему в маткаде
В разделе 1.9 технология работы с пользовательскими функциями, которые можно описать с помощью одного выражения. Если описания функции нельзя уместить в одно выражение, то без элементов программирования обойтись сложно.
Язык программирования MathCAD содержит все элементы языка высокого уровня, необходимые для математических расчетов. Будучи дополненным сотнями встроенных функций и операторов системы, возможностями численного и символьного расчета различных величин, он по эффективности не уступает профессиональным системам программирования. Кроме того, у него есть одно очень крупное преимущество: язык программирования MathCAD предельно прост (а по изящности и наглядности в оформлении алгоритмов вообще не имеет аналогов).
4.1. Спецификации функций
Спецификация функции состоит из ее заголовка и описания назначения – выходного значения или результата работы функции. Для примера можно обратиться к мастеру функций и более внимательно посмотреть на предоставляемые им для его функций описания. На рис. 4.1 открыта страница со спецификацией функции rnorm.


Рис. 4.1. Спецификация функции, предоставляемая мастером функций
При описании назначения функции необходимо сказать, что возвращает функция в качестве своего результата (в описываемой функции rnorm возвращает вектор нормально распределенных случайных значений). При этомобязательно нужно пояснить роль каждого из формальных параметров, перечисленных в заголовке (m – количество значений, mu – среднее значение, sigma – стандартное отклонение). Желательно сказать об ограничениях, т.е. невозможность расчета при … каких-либо условиях.
Для написания программ-функций в системе MathCAD предусмотрена специальная панель программироваия –Programming (Программирование), содержащая все операторы и элементы языка. Общий вид панели Programmingпредставлен на рис. 4.2. Операторы в программу вставляются только с помощью кнопок этой панели.
Назначение основных команд, представленных на панели:

Add Line – добавление новой строки в программу или создание заготовки программы из двух строк, если программы еще не существует;
← – присвоение значения локальной переменной;
if – условный оператор. Позволяет в зависимости от условия выполнять или не выполнять те или иные действия;
otherwise – используется сразу после оператора if и позволяет выполнить определенные действия при невыполнении условия в операторе if ;
for – оператор создания цикла со счетчиком;
while – оператор создания цикла, выполнение которого продолжается до тех пор, пока выполняется указанное условие.
continue – продолжить вычисления в цикле;
break – прервать вычисления в цикле;
return – оператор возврата;
on error – оператор перехода при возникновении ошибки.
Рис.4.2. Вид панели инструментов Programming ( Программирование)
Чтобы написать программу, прежде всего для нее должен быть создан специальный, обособленный от остального документа, программный блок-тело функции. Выглядит он как черная вертикальная линия с маркерами, в которые заносятся те или иные выражения и операторы алгоритма. Чтобы построить единичный элемент программного блока, нажмите кнопку команды Add Line (Добавить линию) панели Programming (Программирование).
Присваивание значений в программах имеет ряд особенностей. Важнейшим из них является то, что присвоение величин используемым алгоритмом функциям и переменным может быть произведено как в самой программе, так и выше нее. Данные два подхода весьма существенно разнятся:
Если программа должна осуществлять какую-то модификацию объекта, то результат своей работы она должнавозвращать.
Все программы составляемые в пакете MathCAD с точки зрения любого языуа программирования (например, Turbo Pascal) представляют собой подпрограммы – функции, которые могут возвращать в качестве результата число, вектор или матрицу.
Заметим, что если программа используется для вычисления одного значения, то в своем заголовке она не содержит списка формальных параметров и называется программой-скаляром.
Программа-функция может не иметь формальных параметров и тогда, когда данные передаются через имена переменных, определенных выше описания программы-функции. Эти переменные будут являться глобальными для данной функции.
Технология создания программы-функции в рабочем документе MathCAD состоит из следующих шагов:
Ввести заголовок функции.
Выполнить команду Add line, расположенную на панели Programming (Программирование). Появившейся на экране шаблон с вертикальной чертой и полями для ввода операторов будут составлять заготовку для тела программы-функции.
Вписать операторы в шаблон-заготовку. Тело программы-функции может включать любое число операторов: локальных операторов присваивания, условных операторов и операторов цикла, а также вызов других программ-функций.
Самое нижнее поле всегда предназначено для определения возвращаемого программой значения.

Пример 1. Требуется подготовить описание функции и вычислить значения этой функции приx = 4.15 и g = 1.854.




Рис.4.3. Пошаговое создание и выполнение программы-функции
В данном примере введена вспомогательная локальная переменная t для вычисления значения функции. И эта переменная расположена в последней строчке программного блока. В пункте (6) приведена операция вычисления функции для фактических значений. На рис. 4.4, b, c приведены другие варианты решения поставленной задачи.



Рис. 4.4. Демонстрация элементов программирования простых выражений

В примере, представленном на рис. 4.4, в первой колонке a для вычисления значения используется базовый набор средств без элементов программирования. Во второйb и третьей c колонках производятся точно такие же вычисления, но с использованием элементов программирования. Обе программы (b и c) можно считать эквивалентными, так как возвращают они одно и то же значение, которое располагается в последней строчке программируемой части. В (bи c) мы имеем дело с программой – скаляром, так как они используются для вычисления одного значения и не имеют формальных параметров.
Внутри программ (b и c) используются глобальные переменные g и x из документа. Значения этих переменных определены заранее. Обе программы из примера, представленного на рис. 4.4, в своей программируемой части содержат операторы присваивания с использованием локальных переменных. Переменные, созданные внутри программы с таким видом присваивания, являются внутренними, и доступ к ним может осуществляться только в самой программе.

Впрограммной части используются глобальные переменные обычнотолько как операнды в выражениях.
Последняя строка программы не должна содержать управляющих операторов. Эта строка задает значение, возвращаемое программой, т.е. получает результат вычислений и может содержать имя локальной переменной результата (рис. 4.4, c) или выражение, вычисляющее результат (рис. 4.4, b).
Обычно программа содержит больше чем две строки, поэтому рекомендуется сразу задавать блок из 5-6 маркеров.
Добавление недостающих полей для ввода дополнительных операторов производится с помощью кнопки Add lineпанели программирования. При этом поле ввода добавляется внизу выделенного к этому моменту оператора.
Для удаления того или иного оператора или поля ввода из тела программы-функции, нужно заключить его выделить и нажать клавишу .
Программный блок можно создать и внутри уже заданного блока (вложенный блок). Для этого следует использовать один из стандартных способов: поставить курсор в маркер соответствующего оператора программирования и выполнить Add line.
Иногда при написании программы бывает нужным добавить строку к уже созданному блоку. Чтобы это сделать, поставьте курсор в ту строку блока, выше или ниже которой должна быть введена строка, и нажмите клавишу . При этом строка будет выделена и можно будет произвести добавление одним из стандартных способов.
Положение вставляемого маркера определяется положением вертикальной черты курсора. Если она находится слева от выделенного выражения, то маркер будет добавлен выше выделенной строки, если справа – то ниже.
Чтобы развернуть курсор в нужную сторону, нажмите клавишу .
Чтобы добавить строку к целому блоку, его следует выделить, дважды нажав клавишу .
В том случае, если программа содержит блоки различных уровней, то для добавления строки, например, к первому блоку, нажмите клавишу несколько раз: при каждом нажатии будут выделяться блоки более низкого уровня.
Пример 2. Требуется найти действительные корни квадратного уравнения , гдеa, b, c – любые действительные числа и . Известно, что в зависимости от знака дискриминантадействительные корни уравнения могут быть получены по формуле:

Решение . Опишем вычисление корней в виде программы-функции.

Спецификацию для этой функции можно записать следующим образом. Функция R ( a,b,с ) возвращает значения действительных корней квадратного уравнения или сообщает о том, что уравнение не имеет корней.
Здесь a , b , с – коэффициенты уравнения.
Очевидно, что в данном случае мы имеем дело с ветвящимся процессом.
Программирование ветвящихся процессов требует проверки некоторых условий, в зависимости от которых выбирается вычислительная формула. Для реализации таких вычислений на панели программирования предусмотрен оператор if (если).

При включении оператора if в блок программирования появляется шаблон с двумя полями ввода – справа и слева от оператора:
if .
В поле ввода справа от оператора записывается условие. Для ввода условий следует использовать панельBoolean (Логические), где есть кнопки для проверки условий ( = > Рис. 4.6. Демонстрация элементов программирования ветвящихся процессов

Рис. 4.7. Демонстрация элементов программирования ветвящихся процессов
На рис. 4.8 представлены примеры программ-функций, реализующих вычисления, содержащие ветвящиеся процессы.






Рис. 4.8. Примеры программирования функций с проверкой условий. Здесь x – глобальная переменная
Пример 4. Требуется найти максимальный и минимальный элементы в заданном массиве.
Решение. Задача поиска наибольшего/наименьшего значений в заданном массиве относится к типовым циклическим алгоритмам .
Спецификацию для этой функции можно записать следующим образом:
Функция Fun(P) возвращает наибольшее и наименьшее значение в массиве Р.
Для создания циклов в MathCAD предусмотрено два оператора: for и while. Поскольку количество повторений цикла заранее известно и связано с числом элементов заданного массива, в данном решении целесообразно использовать оператор for.

После вставки оператораfor в строку программы его сопровождают три поля ввода, как это показано на рис. 4.9.

Рис. 4.9. Шаблон оператора цикла for
В поле ввода после слова for следует указать имя переменной-счетчика. Это может быть любое имя, которое не использовалось ранее в программе. Внутри цикла можно использовать эту переменную в любых выражениях, нельзя только присваивать ей никакого значения.
В поле ввода после знака € следует указать диапазон значений, которые будет принимать переменная-счетчик. Вместо диапазона в данном поле ввода можно указать имя некоторого массива (вектора или матрицы). В таком случае переменная-счетчик будет последовательно принимать значения всех элементов этого массива. Количество повторов цикла будет равно количеству элементов массива.
В поле ввода под словом for следует ввести тело цикла
Обозначим имя переменной-счетчика, которая используется в операторе for – буквой t. Для описания алгоритма воспользуемся тем, что в операторе цикла для переменной-счетчика можно указать в качестве диапазона имя массива. Как сказано выше, в таком случае переменная t будет последовательно принимать значения всех элементов указанного вfor массива (в нашем случае – это массив Р). Для обозначения максимального и минимального значений в программу введем две вспомогательные переменные Pmax и PMin. Тогда описание функции может быть представлено в виде, как это показано на рис. 4.10.
Отметим, что в данном случае в качестве результата работы функции нужно вернуть два значения, а специфика функции в MathCAD такова, что она позволяет вернуть только одно значение, но при этом сказано, что функция в качестве результата может вернуть, в том числе, вектор и матрицу. Поэтому при формировании результата мы определим его как вектор из двух значений.
Справа от программы-функции, представленной на рис. 4.10, написаны операторы, предназначенные для создания вектора с именем U из шести элементов. Для этого введена вспомогательная переменная i, задающая диапазон изменения индекса массива, а значения элементов массива U формируются с помощью функции rnd – датчика случайных чисел. Параметр 20 в ней определяет диапазон принимаемых значений.
На рис. 4.11, a представлен второй вариант программы-функции, в котором в качестве диапазона значений для переменной-счетчика цикла for берется диапазон изменения индекса массива. Поэтому в список формальных параметров в заголовок функции вносится еще один параметр n, который указывает верхнюю границу изменения индекса.
Mathcad является универсальным инструментом у тех людей, которые плотно связали свою жизнь с вычислениями. "Маткад" способен производить сложные математические расчеты и мгновенно выдавать ответ на экране. Студенты или те, кто в первый раз столкнулся с этой программой, задают множество вопросов, на которые не могут дать ответ самостоятельно. Один из них, затрудняющий дальнейшее обучение: как построить график в "Маткаде"? На самом деле, это не так сложно, как может показаться. Постараемся разобраться также в том, как в "Маткаде" построить график функции, как строить несколько функций, узнаем о некоторых элементах отображение графика на экране.
Быстрый график в Mathcad
Вам будет интересно: Пуристы - это. Значение слова
Возьмем одну функцию и будем проводить все ниже перечисленные операции с ней. Допустим, имеем следующее техническое задание: построить график функции f(x) = (e^x/(2x-1)^2)-10 на интервале [-10;10], исследовать поведение функции.
Итак, перед тем как построить график в "Маткаде", нужно переписать нашу функцию в математическую среду. После этого просто прикинем возможный график без масштабирования и всего прочего.
Построение дополнительных графиков
Чтобы понять, как построить несколько графиков в "Маткаде", добавим к нашему техническому заданию небольшое дополнение: построить график производной от заданной функции. Единственное, что нам нужно - в поле графика добавить производную по переменной "x".
График, построенный по набору значений
Перед тем как построить график в "Маткаде" по точкам, необходимо создать диапазон значений. Сразу отметим, что график, построенный по точкам, иногда бывает неточным, так как может найтись такая точка, которая не попадет в диапазон значений, но в оригинальном графике в ней происходит разрыв. В этом примере специально будет показан этот случай.
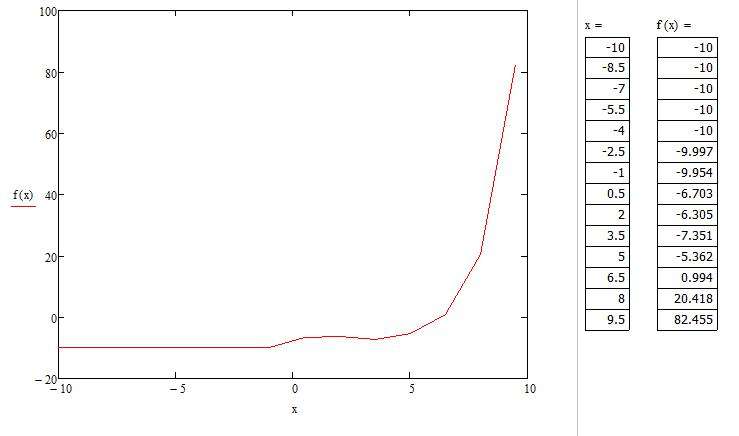
Мы видим, что на графике, построенном по точкам, не отображается та точка, которая осуществляет разрыв на исходном графике. То есть можно сделать вывод о том, что построение по точкам может не учитывать значения функции, которые создают разрыв.
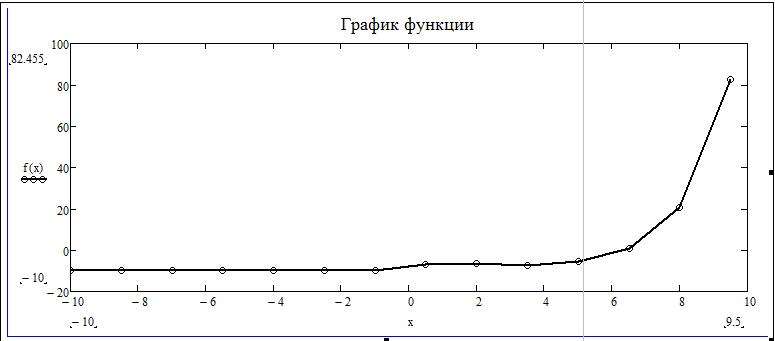
Настройка отображения графика
В этой статье мы уже затрагивали настройки графика. Окно с настройками вызывается двойным нажатием левой кнопкой мыши по графику. В окне форматирования графика есть пять разделов. "Оси X, Y" - содержит информацию про координатные оси, а также отображения вспомогательных элементов. Второй раздел "Трассировка" связан с кривыми линиями построения графика, здесь можно корректировать их толщину, цвет и другое. "Формат числа" отвечает за отображение и расчет единиц. В четвертом разделе можно добавлять подписи. Пятый раздел " По умолчанию" выводит все настройки в стандартную форму.
Пример 1. Составить программу для вычисления корней квадратного уравнения: ax 2 + bx + c = 0 по известной формуле:
Алгоритм (1) является линейным и фрагмент документа MathCAD содержит конструкции, приведенные на рис 1.
П рограммирование разветвляющихся алгоритмов
Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких возможных ветвей вычислений. Выбор конкретной ветви зависит от выполнения (или не выполнения) заданных условий на значения переменных алгоритма.
Пример 2. Значение переменной y зависит от значений переменной x и определяется выражением:
Для реализации разветвляющегося алгоритма необходимо использовать:
· конструкции, проверяющие выполнение заданных условий;
· конструкции, выбирающие нужную ветвь вычислений в зависимости от результатов проверки заданных условий.
Для проверки заданных условий в MathCAD используется: выражение отношений, логические операции и логические выражения.
Выражением отношений (или просто отношением) называется конструкция вида:
где , - произвольные арифметические выражения, - любая из следующих операций: (здесь вертикальные чёрточки являются разделительным символом при перечислении).
Для ввода знаков операций отношений можно использовать палитру Булево (приведённую на рис.3) или использовать клавиши, обозначения которых приведены в таб. 1.

Палитра инструментов БУЛЕВО
Внимание! Не следует путать знак операции сравнения = с похожим знаком вывода значений переменных. Знак операции = имеет больший размер и более жирное начертание.
Выражение отношений принимает одно из двух значений: 1 - если заданное отношение выполняется или 0 – в противном случае. Значение 1 можно интегрировать как значение истина, а 0 – как ложь .
Задание 1 . Пусть значения целой переменной x =3 . Определить значение следующих выражений отношений:
Для проверки более сложных условий используются четыре логических операций, обозначение которых приведены в табл. 2
Таблица 2
Логическое отрицание ( NOT )
Логическое ИЛИ ( OR )
Логическое И ( AND )
Исключающее ИЛИ ( XOR )
Знаки этих операций вводится с палитры Булево . Результат выполнения этих операций, приведен в табл. 3.
Логическим выражением называется конструкция, состоящая из выражений отношений, логических операций и круглых скобок. Логическое выражение принимает только одно из двух значений: 1 или 0; вычисляется слева направо с учетом приоритета входящих в выражение операции. Наивысший приоритет круглые скобки, а затем по убыванию: AND , OR и XOR – одинаковый приоритет и самый низкий приоритет выражения отношений.
Задание 2 . Определите порядок вычисления значений логических выражений в документе MathCAD , приведенных на рисунке 3
Рис. 3 Примеры логических выражений
Пример 2. Записать логическое выражение, принимающее значение 1 при попадании точки с координатами ( x , y ) в первую четверть.
Логическое выражение имеет вид
Для выбора нужной ветви разветвляющегося алгоритма используется конструкция, названная условной функцией if , записывается в виде:
if ( , , ),
где имя функции if вводится с клавиатуры.
Если логическое выражение равно 1, то значение функции определяется выр.1, в противном случае – выр. 2. Блок-схема этой функции приведена на рис. 4.
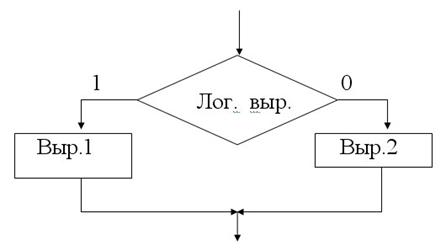
Рис. 4. Блок-схема функции if
При программировании разветвляющихся алгоритмов с тремя и более вычислительных ветвей на месте выр. 1 и выр. 2 вновь может использоваться функция if .
Пример 3. Используя условную функцию if запрограммировать два разветвляющихся алгоритма:
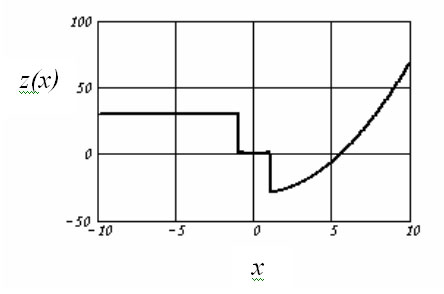
Рис. 5. Реализация разветвляющихся алгоритмов
В MathCAD имеется ряд встроенных функций, которые возвращают результат, зависящий от знака или величины аргумента и которые могут использоваться при программировании разветвляющихся алгоритмов. Приведем некоторые из них:
· ceil ( x ) – наименьшее целое, большее или равное x ;
· trunc ( x ) – целая часть вещественного числа x ;
· floor ( x ) – наибольшее целое, меньшее или равное x ;
· round ( x , n ) – округленное значение вещественного x с точностью до n знаков после десятичной точки;
· Ф( x ) – функция Хевисайда – равна 0 при x и 1 в противном случае;
· sign ( x ) – функция знака (равна 0 если x = 0; -1, если x и 1 , если x >0 );
· signum ( x ) – возвращает 1, если x = 0 и в остальных случаях.
Программирование циклических алгоритмов
Типы циклов. П о способам организации цикла можно выделить:
а) цикл типа арифметической прогрессии;
б) итерационный цикл.
Программирование цикла типа арифметической прогрессии
Особенностью цикла типа арифметической прогрессии является изменение параметра цикла по закону арифметической прогрессии и поэтому можно, не выполняя цикла, определить количество повторений цикла.
Параметр такого цикла задается дискретной переменной и тогда конструкции, входящие в тело цикла располагаются, начиная от этого описания и до конца документа MathCAD или до конструкции, переопределяющей дискретную переменную – параметр цикла.
Этот цикл имеет уже два параметра: i – параметр, определяющий номер строки; j – параметр, определяющий номер столбца матрицы. Заметим, что такой цикл называется двойным циклом.
Заметим, что если параметр цикла не входит в индексные выражения элементов массива, то он может принимать вещественные значения.
Заметим, что во фрагментах, приведенных на рисунках системная переменная ORIGIN =1.
Лабораторная работа №4 Расчетное моделирование САР в Mathcad
К лабораторной работе
Цель работы.
Цель работы - расчетное построение переходных характеристик САР по передаточной функции для типового воздействия методами:
А) обратного преобразования Лапласа;
Б) решением системы обыкновенных дифференциальных уравнений (ОДУ) для разложения передаточной функции с помощью дополнительных переменных.
Моделируемая САР – САР с пропорциональным (П), пропорционально-интегральным (ПИ), пропорционально-дифференциальным (ПД) и пропорционально-интегрально-дифференциальным (ПИД) регуляторами.
Продолжительность работы - 4 часа.
1. Построение передаточных функций САР.
Структурная схема одноконтурной САР может быть представлена в виде, указанном на рис.1.

G(p) – изображение задающего воздействия g(t), X(p) – изображение рассогласования x(t)=g(t)-yoc(t), F(p) – изображение возмущающего воздействия f(t), Y(p) – изображение регулируемой величины, Yoc(p) – изображение сигнала обратной связи yoc(t), W1(p) – передаточная функция исполнительного механизма, W2(p) – передаточная функция объекта регулирования, Woc(p) – передаточная функция обратной связи.
Рис.1. Структурная схема одноконтурной САР.
Задачей САР с ПИД-регулятором является поддержание заданного значения измеряемой (регулируемой) величины. ПИД-регулятор измеряет отклонение стабилизируемой величины от заданного значения (уставки) и выдаёт управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально этому отклонению, второе пропорционально интегралу отклонения и третье пропорционально производной отклонения (или, что то же самое, производной измеряемой величины). Условное изображение ПИД-регулятора представлено на рис.2.

Рис.2. Схема, иллюстрирующая принцип работы ПИД-регулятора
Если какие-то из составляющих не используются, то регулятор называют: Пропорциональным, пропорционально-интегральным, Пропорционально-дифференциальным,.
Пропорциональная Составляющая. Пропорциональная составляющая вырабатывает выходной сигнал, который стабилизирует отклонение регулируемой величины. Выходной сигнал пропорциональной составляющей тем больше, чем сильнее регулируемая величина отклоняется от уставки. Если входной сигнал равен уставке, то выходной равен нулю.
При использовании пропорционального регулятора значение регулируемой величины никогда не стабилизируется на заданном значении. Существует так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. Например, в регуляторе температуры выходной сигнал (мощность нагревателя) постепенно уменьшается при приближении температуры к уставке, и система стабилизируется при мощности равной тепловым потерям. Температура не может достичь уставки, так как в этом случае мощность нагревателя станет равна нулю, и он начнёт остывать.
Чем больше коэффициент пропорциональности между входным и выходным сигналом (коэффициент усиления), тем меньше статическая ошибка, однако при слишком большом коэффициенте усиления могут начаться автоколебания, а при дальнейшем увеличении коэффициента система может потерять устойчивость.
Дифференциальная составляющая. Дифференциальная составляющая противодействует предполагаемым отклонениям регулируемой величины, которые могут произойти в будущем. Эти отклонения могут быть вызваны внешними возмущениями или запаздыванием воздействия регулятора на систему. Чем быстрее регулируемая величина отклоняется от уставки, тем сильнее противодействие, создаваемое дифференциальной составляющей.
Выходной сигнал ПИД регулятора u(t) определяется тремя слагаемыми:

,
Где Кp, Кi, Кd — коэффициенты усиления пропорциональной, интегральной и дифференциальной составляющих регулятора, соответственно.
Большинство методов настройки ПИД-регуляторов используют несколько иную формулу для выходного сигнала, в которой на пропорциональный коэффициент усиления умножены также интегральная и дифференциальная составляющие:

Часто в качестве параметров ПИД-регулятора используются:

· постоянные интегрирования и дифференцирования, имеющие размерность времени

![]()
В соответствии с рис.1 и рис.2 схему САР с ПИД-регулятором можно представить в виде, изображенном на рис.3.

Рис.3. САР с ПИД-регулятором.
Для анализа САР предположим, что объект регулирования представляет собой инерционное или апериодическое звено. Каждое звено САР, представленной на рис.3, имеет свое уравнение и передаточную функцию (см. таблицу 1).
Читайте также:


