Как сделать сдвиг в массиве java
© 2008 Наталия Македа
Все материалы блога защищены авторским правом. Любая перепечатка или использование материалов этого блога в коммерческих целях возможна лишь с письменного согласия автора. При некоммерческом использовании ссылка на блог обязательна.
четверг, 15 мая 2008 г.
2.4. Операторы сдвига > и >>>(Выпуск 7)
В Java есть операторы сдвига. Операторы > позаимствованы из С/C++. Кроме того, Java обладает своим новым оператором сдвига >>>.
Операторы сдвига присущи системам, которые могут выравнивать биты, прочтённые из IO портов или зартсываемые в IO порты. Это также быстрое умножение или деление на степень двойки. Преимущество операторов сдвига в Java - это независимость от платформы. Поэтому вы можете использовать их не беспокоясь ни о чём.
Основы сдвига
Сдвиг - это, по сути, простейшая операция: мы берём последовательность битов и двигаем её влево или вправо. Больше всего конфуза вызывает оператор >>>. Но о нём мы поговорим чуть позже.
Операторы сдвига могут применяться лишь к целым числам, то есть к типам int или long . Следующая таблица иллюстрирует базовый механизм сдвига.
Таблица показывает фундаментальную идею сдвига: перемещение битов относительно их позиций. Это как очередь в магазине: как только один человек совершил покупку и отшёл, вся очередь сдвинулась и позиции всех участников очереди изменились.
Однако, глядя на таблицу, возникают три вопроса вопроса:
- Что происходит, если мы сдвигаем влево и при этом часть бинарной записи выходит за границу слева, а часть - остаётся пустой справа?
- Что происходит, когда справа - выход за границы, а слева - пустое место?
- Какое истинное значение принимает знак "?"?.
Ответим на часть этих вопросов. Биты, вышедшие за границы, просто теряются. Мы о них забываем.
В некоторых языках, типа ассемблер, есть операция ротации, когда при сдвиге вышедшие за границы биты не теряются, но ставятся на освободившееся место (вместо вопросиков). Однако языки высокого уровня, типа Java, не имеют в своём арсенале такой операции.
Сдвиг отрицательных чисел
Ответ на вопрос о значении символов "?" в приведенной выше таблице требует отдельного рассмотрения.
В случае сдвига влево >> новые биты просто устанавливаются в ноль. В случае сдвига вправо со знаком >> новые биты принимают значение старшего (самого левого) бита перед сдвигом. Следующая таблица демонстрирует это:
Заметьте: в том, случае, где старший бит был 0 перед сдвигом, новые биты стали тоже 0. Там где старший бит перед сдвигом был 1, новые биты тоже заполнились 1.
Это правило может показаться странным на первый взгляд. Но оно имеет под собой очень серьёзное обоснование. Если мы сдвигаем бинарное число влево на одну позицию, то в десятичной записи мы умножаем его на два. Если мы сдвигаем влево на n позиций, то умножение происходит на 2 n , то есть на 2, 4, 8, 16 и т.д.
Сдвиг вправо даёт деление на степени двойки. При этом, добавление слева нулей на появившиеся биты на самом деле даёт деление на степени двойки лишь в случае положительных чисел. Но для отрицательных чисел всё совсем по другому!
Как известно, старший бит отрицательных чисел равен единице, 1. Для того, чтобы сохранить старшинство единицы при сдвиге, то есть сохранить отрицательный знак результата деления отрицательного числа на положительное (степень двойки), нам нужно подставлять единицы на освободившиеся места.
Если мы посмотрим на Таблицу 2, то заметим, что 192, сдвинутое на 1 бит вправо - это 192/2=96, а сдвинутое на 7 битов вправо - это 192/2 7 =192/128=1 по законам целочисленной арифметики. С другой стороны, -192 сдвинутое на 1 бит вправо - это 192/2=-96 и т.д.
Есть, однако пример, когда реультат сдвига вправо отличается от результата целочисленного деления на 2. Это случай, когда аргумент = -1. При целочисленном делении мы имеем: -1/2=0. Но результат сдвига вправо нам даёт -1. Это можно трактовать так: целочисленное деление округляет к нулю, а сдвиг округляет к -1.
Таким образом, сдвиг вправо имеет две ипостаси: одна (>>>) просто сдвигает битовый паттерн "в лоб", а другая (>>) сохраняет эквивалентность с операцией деления на 2.
Зачем же Java потребовался беззнаковый сдвиг вправо (сдвиг "в лоб"), когда ни в С, ни в С++ его не существует? Ответ прост, потому что в С и С++ сдвиг всегда беззнаковый. То есть >>>> в Java - это и есть сдвиг вправо в C и C++. Но, поскольку в Java все численные типы со знаком (за исключением char ), то и результаты сдвигов должны иметь знаки.
Сокращение (reduction) правого операнда
На самом деле у операторов сдвига есть правый операнд - число позиций, на которое нужно произвести сдвиг. Для корректного сдвига это число должно быть меньше, чем количество битов в результате сдвига. Если число типа int (long) , то сдвиг не может быть сделан более, чем на 32 (64) бита.
Оператор же сдвига не делает никаких проверок данного условия и допускает операнды, его нарушающие. При этом правый операнд сокращается по модулю от нужного количества битов. Например, если вы захотите сдвинуть целое число на 33 бита, то сдвиг произойдёт на 33%32=1 бит. В результатае такого сдвига мы легко можем получить аномальные результаты, то есть результаты, которых мы не ожидали. Например, при сдвиге на 33 бита мы ожидаем получить 0 или -1 (в знаковой арифметике). Но это не так.
Почему Java сокращает правый операнд оператора сдвига или грустная история о заснувшем процессоре
Одной из главной причин введения сокращения было то, что процессоры сами сокращают подобным образом правый операнд оператора сдвига. Почему?
Несколько лет назад был создан мощнейший процессор с длинными регистрами и операциями ротации и сдвигам на любое количество битов. Именно потому, что регистры были длинными, корректное выполнение этих операций требовало несколько минут.
Основным применением данных процессоров был контроль систем реального времени. В данных системах самый быстрый ответ на внешнее событие должно занимать не более задержки на прерывание (interrupt latency). Отдельные инскрукции таких процессоров были неделимы. Поэтому выполнение длинных операций (сдвига на несколько бит и ротации) нарушало эффективную работу процессора.
Следующая версия процессора имплементировала эти операции уже по-другому: размер правого операнда сократился. Задержка на прерывание восстанавилась. И многие процессоры переняли данную практику.
Арифметическое распространение (promotion) операндов
Апифметическое распространение операндов происходит перед применением оперции сдвига и гарантирует, что операнды по крайней мере типа int . Это явление имеет особый эффект на беззнаковый сдвиг вправо, когда сдвигаемое число меньше, чем int : мы получаем не тот результат, который ожидали.
Если смещение не всегда одинаковое, т.е. мне, возможно, придется использовать ту же функцию для изменения размера 2 или 4 символов, что было бы хорошим способом циклического смещения значений массива байтов на 2 позиции * параметр? Это то, что у меня есть
задан 23 марта '11, 23:03
Блин, я имел ввиду j вместо param. Отредактирую - dLobatog
1 ответы
Во-первых: если возможно, используйте java.util.BitSet для подобных задач.
Не уверен, но как-то у самого BitSet сдвига нет, но этот источник похоже реализовал это.
ответ дан 24 мар '11, в 03:03
Почему Bitset лучше, чем стандартные массивы byte []? - dЛобатог
Не тот ответ, который вы ищете? Просмотрите другие вопросы с метками java bytearray bit-shift or задайте свой вопрос.
Представьте себе такую задачу. Вам нужно хранить в памяти компьютера значения линейной функции при . Как это сделать? Мы умеем создавать отдельные переменные, но тогда здесь нам понадобится 100 переменных, с которыми надо будет еще как-то управляться. Но, к счастью, все можно сделать гораздо проще. Можно задать массив из 100 элементов и в каждый элемент массива записать значение функции при конкретном значении x.
Итак, чтобы задать массив в языке Java используется такой синтаксис:
Например, в нашем случае следует выбрать вещественный тип данных для элементов массива. Имя массива обозначим как и функцию y:
и далее можем создать массив со 100 элементами с помощью оператора new:
Эти две строчки можно объединить в одну и записать все так:
Все, мы создали массив. Теперь, чтобы в его первый элемент записать первое значение функции, используется такой синтаксис:
Здесь k, b – переменные с какими-либо значениями, а x=0. Обратите внимание, первый элемент массива всегда имеет индекс, равный нулю. По аналогии, записывается значение во второй элемент массива:
и так далее. Давайте напишем целиком программу, которая заносит все 100 значений в массив и выводит их на экран.
Обратите внимание, если мы хотим прочитать значение из массива, то достаточно просто обратиться к нему по соответствующему индексу, например, так:
В результате переменная a будет равна 6-му значению элемента массива y. Поэтому, когда мы пишем
то осуществляется вывод элемента массива с индексом x. Вот так можно записывать и считывать значения из массива.
В языке Java можно сразу инициализировать массив конкретными значениями в момент его объявления, например, так:
В этом случае элементу powers[0] присваивается значение 1, powers[1] – 2, и т.д. Обратите внимание, что в этом случае нигде не должен указываться размер массива. Его размер определяется числом инициализируемых элементов.
Выведем этот массив в консоль:
Смотрите, здесь для определения числа элементов в массиве использовалось его свойство length. То есть, индекс последнего элемента в массиве всегда равен length-1. Например, вывести только последний элемент нашего массива можно так:
Для хранения некоторых видов информации, например, изображений удобно пользоваться двумерными массивами. Объявление двумерных массивов осуществляется следующим образом:
Какой индекс здесь считать строками, а какой – столбцами, решает сам программист, компьютер все равно будет обрабатывать элементы этого массива в соответствии с программой и что такое строки и столбцы ему неведомо.
Здесь также, первый элемент массива имеет индексы 0, то есть,
а далее, уже так:
и так далее. Давайте в качестве примера напишем программу, которая бы записывала в массив E размерностью 10x10 такие значения:
Также в Java можно создавать так называемые многомерные зубчатые массивы. Визуально такой двумерный массив можно представить вот в таком виде:
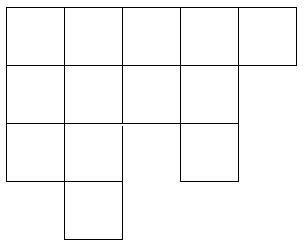
А задать его можно так:
Для обработки элементов такого массива можно записать такие циклы:
Смотрите, что здесь получается. Вот это свойство z.length возвращает первую размерность массива, то есть 5. Далее, мы берем i-ю строку (либо столбец в зависимости от интерпретации) и узнаем сколько элементов в этой строке. И внутри второго цикла записываем туда значение cnt, которое постоянно увеличивается на 1.
Затем, мы выводим полученный массив в консоль. Здесь также сначала перебираем первую его размерность. А вот этот цикл перебирает по порядку все элементы i-й строки и помещает их в переменную val. Обратите внимание на его синтаксис:
Вот так можно перебирать элементы любой коллекции, в данном случае строки массива. Вот так все это работает. По аналогии можно задавать массивы любой размерности.
Обработка элементов массива
- Удаление значения из массива по определенному индексу.
- Вставка значения в массив по определенному индексу.
- Сортировка элементов массива.
Начнем с первого – удаления элемента из массива. Создадим вот такой массив:
запишем туда значения с 1 по 9:
Теперь удалим элемент со значением 6. Для этого нужно проделать такую операцию:
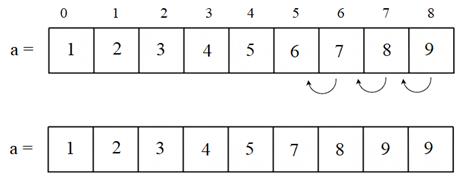
Теперь реализуем второй алгоритм и вставим значение 4, которого не хватает вот в таком массиве:
Здесь в конце записаны две 9, чтобы мы могли сдвинуть все элементы на 1 вправо и вставить элемент со значением 4. То есть, нам следует выполнить такую операцию над элементами массива:
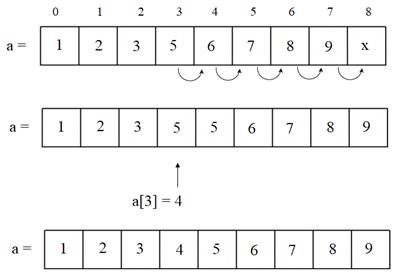
Обратите внимание, что сдвиг осуществляется с конца массива. Если мы начнем это делать с 4-го, то просто затрем все остальные значения пятеркой. Итак, вот программа, которая вставляет 4-ку в этот массив:
Теперь рассмотрим довольно распространенный алгоритм сортировки элементов массива по методу всплывающего пузырька. Реализуем его на языке Java.
Здесь первый цикл показывает с какого элемента искать минимальный, то есть, это местоположение той вертикальной черты в методе всплывающего пузырька. Затем, задаем две вспомогательные переменные min – минимальное найденное значение, pos – индекс минимального элемента в массиве. Второй вложенный цикл перебирает все последующие элементы массива и сравнивает его с текущим минимальным и если будет найдено меньшее значение, то min становится равной ему и запоминается его позиция. Вот эти три строчки меняют местами текущее значение элемента с найденным минимальным, используя вспомогательную переменную t. И в конце программы выполняется вывод элементов массива на экран.
Запустим эту программу и посмотрим как она работает. Кстати, если мы теперь хотим выполнить сортировку по убыванию, то достаточно изменить вот этот знак на противоположный.
Видео по теме











© 2022 Частичное или полное копирование информации с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все тексты и изображения являются собственностью сайта
Есть ряд способов сдвинуть массив влево на N элементов. Можно взять и сделать N сдвигов по одному элементу, получив квадратичную сложность. Можно создать целевой массив по размеру исходного и вычислить положение каждого элемента после сдвига. Хорошо, но скорость линейна, затраты по памяти - тоже.
Если чутка подумать, то можно придумать реализацию, которая мутирует массив и дает линейную скорость и константные затраты по памяти. Но есть один очень элегантный способ – из 3-х строк на основе чудо Span of T из System.Memory:
Идея такая: чтобы сдвинуть массив из K элементов на N элементов влево, нужно перевернуть первые N элементов в массиве, затем последние K - N -1 элементов, а затем перевернуть весь массив:
Получается два прохода по массиву, но зато с читабельностью решения все очень ОК.
27 комментариев:
Справедливости ради, хочу отметить, что это циклический сдвиг влево.
Не совсем понял мысль. Да, это одна из реализаций циклического сдвига влево. Просто, ИМХО, одна из самых кратких и выразительных.
nit: Мне показалось, что Vasya всего лишь хотел справедливо заметить, что слово "сдвиг" в заголовке и теле поста лучше бы заменить на "циклический сдвиг".
В своё время этот фокус произвёл на меня большое впечатление. минут 20 рисовал на листике пытаясь понять как этот трюк работает :)
Он же, но чуть с большим wow-эффектом (IMHO) используется в задачке Reverse Words: когда необходимое переставить слова в предложении в обратном порядке. Например: "Michael Jordan" => "Jordan Michael". Необходимо сделать "реверс" каждого слова и потом реверс всей строки целиком, что в конечном итоге даёт практически линейную сложность.
О! Отличный трюк.
З.Ы. Сложность-то линейная, просто коэффициент равен 2.
У меня есть массив объектов в Java, и я пытаюсь потянуть один элемент в начало и сместить остальные на один.
Предположим, у меня есть массив размером 10, и я пытаюсь вытащить пятый элемент. Пятый элемент переходит в положение 0 , и все элементы от 0 до 5 будут сбрасываться на один.
Этот алгоритм неправильно сдвигает элементы:
Как мне это сделать правильно?
Предполагая, что ваш массив
Что делает ваша петля:
Итерация 1: массив [1] = массив [0];
Итерация 2: массив [2] = массив [1];
Что вы должны делать, это
Логически это не работает, и вы должны поменять свой цикл:
В качестве альтернативы вы можете использовать
Вы можете просто использовать Collections.rotate(List list, int distance)
Используйте Arrays.asList(array) для преобразования в List
Манипуляция массивами таким образом подвержена ошибкам, как вы обнаружили. Лучшим вариантом может быть использование LinkedList в вашей ситуации. Со связанным списком и всеми наборами Java управление массивом обрабатывается внутри, поэтому вам не нужно беспокоиться о перемещении элементов вокруг. С LinkedList вы просто вызываете remove , а затем addLast , и все готово.
Читайте также:


