Как сделать развертку конуса
Сегодня мы будем делать конус из бумаги. Причем покажем не один пример создания конуса, а целых 5 самых лучших, рабочих, проверенных временем вариантов.

Конус можно свернуть из офисной бумаги, цветной бумаги, акварельной, ватмана, фоамирана, обоев, пробкового листа, картона и т.д.
Как сделать конус из бумаги (пошаговая инструкция)
Вариант №1
- Бумага;
- Карандаш;
- Ножницы;
- Шаблон или тарелка;
- Клей карандаш или скотч.
На листе бумаги рисуем представленную ниже фигуру. Можно распечатать готовый шаблон, вырезать его и перевести на бумагу. Можно приложить лист бумаги к монитору компьютера с открытым шаблоном, и без нажима карандашом оставить метки на бумаге. Еще можно взять тарелочку отступить вверх от угла бумаги, приложить ее сбоку и обвести полукруг на бумагу. Готовую фигуру вырезаем ножницами.
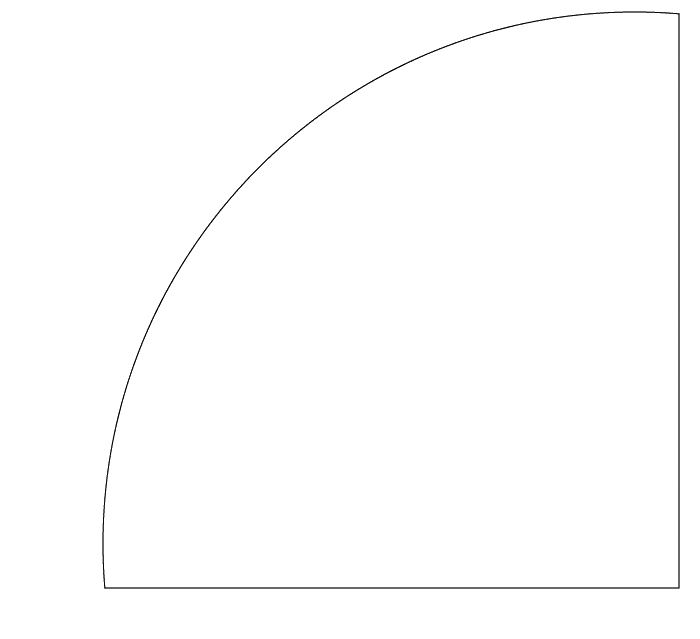
Шаблон конуса для печати или перерисовки.

Сворачиваем заготовку в конус, так чтобы верхушка получилась максимально заостренной. Ну и боковую часть изнутри проклеиваем клеем. Склеиваем изделие в единое целое. Теперь вы знаете, как склеить конус. К слову, вместо клея изнутри можно приклеить полосочку двустороннего скотча или склеить кусочками обычного канцелярского скотча, как снаружи, так и изнутри.

Склеить по внутренней боковой части.

Вариант №2
- Бумага;
- Ножницы;
- Циркуль или тарелка;
- Карандаш;
- Клей или скотч.
На бумаге рисуем окружность при помощи циркуля или обведя по периметру круглую тарелку. Вырезаем круг, сгибаем его по центру и разрезаем ножницами пополам. Получившийся полукруг сворачиваем в конус, так чтобы сверху образовалась острая пика. Ну а внутреннюю боковую часть проклеиваем клеем.

Этапы создания конуса из бумаги.
Вариант №3
- Бумага;
- Ножницы;
- Карандаш;
- Линейка;
- Шаблон, круглая тарелка или циркуль;
- Клей или скотч.
Итак, на листе бумаги нужно нарисовать круг. Это можно сделать при помощи круглой тарелки, циркуля, приложив лист бумаги к монитору компьютера с предварительно открытым шаблоном или просто распечатать готовый шаблон. Далее линейкой нужно очертить внутреннюю часть будущего конуса, как на шаблоне ниже. Вырезаем заготовку, сворачиваем в конус и проклеиваем его боковую сторону.
Шаблон конуса. Вырезать. Свернуть. Склеить. Готовый конус.
Вариант №4
Берем лист бумаги, допустим формата А4. Угол бумаги подгибаем к боковой стенке, лишнюю часть снизу отрезаем. Раскрываем получившийся квадрат и разрезаем его пополам. Получились два треугольника. Берем кончик одного из треугольников, подгибаем его внутрь и сворачиваем конус. Получается идеальный пакетик для семечек! Ну а чтобы конус стал более ровным, надрезаем его верхушку и подворачиваем внутрь (можно ничего не подрезать, просто подвернуть внутрь).

Бумажный конусный пакетик.


Бумажный конус может послужить пакетиком для сладостей, семечек, орешек. А если свернуть бумагу для выпечки, то можно получить кондитерский пакетик для формирования кремовых завитушек на сладкой выпечке. А еще конусы могут служить основой для создания декоративных деревьев, допустим новогодних елочек.
Вариант №5 — быстрый и идеальный конус (видео)
Схемы разных конусов
Белым цветом на схемах выделена часть, которую нужно отрезать. Ну а из розовой части нужно скрутить конус. Соответственно, каждая представленная схема показывает, какой конус по ширине получится в итоге.
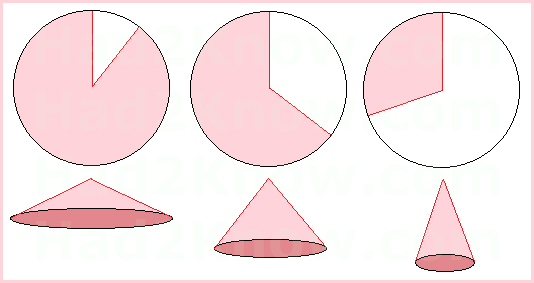
Схемы разных конусов.
Ну вот, теперь вы знаете, как сделать конус из бумаги. Нужно лишь выбрать один из представленных выше вариантов и смело воплотить его в жизнь. Все способы рабочие и неоднократно проверенные временем. Рекомендуем также посмотреть, как сделать маску для сна и комнатные тапочки. Удачных самоделок, и до новых встреч в следующих обзорах!
Выполним одно из простых, но часто используемых в черчении построений – построим развертку конуса (боковой поверхности). В Autocad есть средства, позволяющие быстро и точно решать подобные задачи.
1. Для начала вспомним школьный курс геометрии:

Развертка боковой поверхности прямого конуса – это сектор круга, радиус которого равен образующей конуса R, а длина дуги L=2αr, где r – радиус основания конуса. Угол α в градусах равен 360 * 2α r/2αR = 360r/R.
2. Пусть конус задан графически в виде треугольника (для твердотельного конуса построение также справедливо):

Построим его развертку. Вариантов такого построения очень много, мы же применим способ, который не требует сторонних расчетов и использует только инструменты Autocad. Сначала построим произвольную дугу с радиусом R. Для этого начертим окружность, используя образующую конуса в качестве радиуса:

Затем командой Обрезать (Trim) отсечем от нее любую часть, чтобы она превратилась в дугу. В качестве режущей кромки используем произвольную вспомогательную линию:

Затем линию удаляем, выделяем дугу и открываем окно свойств:

Если в окне свойств не хватает требуемых пунктов настроек, то нажимаем в окне параметров кнопку CUI (Адаптация)

В появившемся окне адаптации пользовательского интерфейса настраиваем отображение требуемых параметров, в нашем случае добавляем параметры Начальный угол (Start angle) и Конечный угол (End angle) и нажимаем Применить.

Изменяем Начальный угол (Start angle) – устанавливаем его в 0. Затем в окошке Конечный угол (End angle) нажимаем значок встроенного калькулятора:



Указываем на экране радиус основания конуса двумя точками (середина основания и нижняя вершина треугольника). Затем c клавиатуры вводим знак деления / и таким же образом указываем длину образующей конуса. В итоге в окне появляется выражение с параметрами вашего конуса:

Жмем Применить (Apply), и угол автоматически вычисляется и присваивается свойству Конечный угол (End angle):

3. Построим основание конуса, чтобы развертка стала полной, и проверим правильность построений. Строим окружность на основании треугольника, как на диаметре, и переносим ее так, чтобы она касалась наружной дуги развертки:

Вот готовая развертка:

Теперь, если по очереди выделить окружность-основание и дугу, можно в свойствах сравнить их длины. У окружности это свойство называется Длина окружности (Circumference), у дуги – Длина дуги (Arc length):

Если построения выполнены правильно, числа должны совпасть.

Как видим, строить развертку конуса (как и многих других геометрических тел) в Autocad гораздо проще, чем на бумаге.
Конус относится к группе тел, образованных путем вращения плоской геометрической фигуры вокруг оси. В случае конуса вращение происходит относительно одного из катетов прямоугольного треугольника.



В зависимости от угла наклона секущей плоскости к основанию конуса могут быть образованы четыре варианта сечений: круг, эллипс, парабола, гипербола.










Популярное
Можно ли проводить дополнительные школьные занятия по геометрии собирая модели многогранников? Конечно же да. Нас пригласили в школу № 2005 (г. Москва), чтобы показать как.
Обработка металла это очень сложный технологический процесс. Но существуют мастера, кто умеет вытачивать многогранники из металла внутри другого.
АРХИМЕД (287 - 212 до н.э.) - древнегреческий математик, физик и механик. Архимед - автор многочисленных открытий и изобретений: машины для.
Многогранники могут стать украшением вашего дома, создав изюминку в интерьере.
Одинаковым узором, повторяющимся на каждой грани многогранника, можно создать чередующуюся комбинацию рисунков на объемном геометрическом теле.
Во второй половине XIX века в школах США зародился новый способ обучения – метод проектов.Согласно этому подходу истинным и ценным является только то, что.
Конус относится к группе тел, образованных путем вращения плоской геометрической фигуры вокруг оси. В случае конуса вращение происходит относительно одного из катетов прямоугольного треугольника.



В зависимости от угла наклона секущей плоскости к основанию конуса могут быть образованы четыре варианта сечений: круг, эллипс, парабола, гипербола.










Популярное
Найти подарок для школьника, который будет интересным, полезным, а также не разорит семейный бюджет – возможно ли такое в 2020 году? Рассказываем, чем можно.
Итальянская компания BULGARI (Булгари), основанная в 1884 году, активно использует в рекламных целях геометрическую форму восьмиугольника для.
Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? Одним лишь вращением мы можем.
Подвесной потолочный светильник или по-простому - люстра, ещё никогда не был так близок к точным математическим формам.
Одинаковым узором, повторяющимся на каждой грани многогранника, можно создать чередующуюся комбинацию рисунков на объемном геометрическом теле.
Обработка металла это очень сложный технологический процесс. Но существуют мастера, кто умеет вытачивать многогранники из металла внутри другого.
Читайте также:


