Как сделать разносторонний треугольник
В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.
Виды треугольников по углам:
- остроугольные
- прямоугольные
- тупоугольные
Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).
Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Виды треугольников по сторонам:
- равносторонние
- равнобедренные
- разносторонние
Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.
Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.
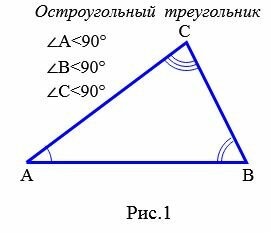
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).
 |
Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).
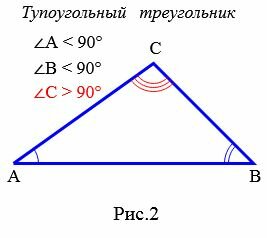 |
Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.
Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).
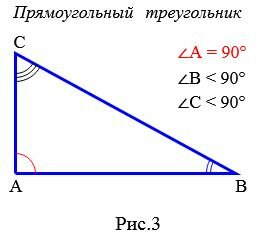 |
Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.
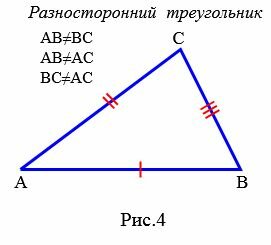
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).
 |
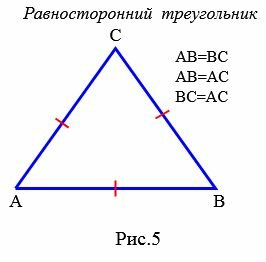
Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).
 |
Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).
 |
В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.
разносторонний треугольник Это трехсторонний многоугольник, где у каждого разные размеры или длины; по этой причине ему дается название лестница, что на латыни означает скалолазание.
Треугольники - это многоугольники, считающиеся простейшими в геометрии, потому что они образованы тремя сторонами, тремя углами и тремя вершинами. В случае разностороннего треугольника, поскольку он имеет все разные стороны, это означает, что его три угла также будут разными..

- 1 Характеристика разносторонних треугольников
- 1.1 Компоненты
- 2.1 Внутренние углы
- 2.2 Сумма сторон
- 2.3 Несовместимые стороны
- 2.4 Неконгруэнтные углы
- 2.5 Высота, медиана, биссектриса и биссектриса не совпадают
- 2.6 Ортоцентр, барицентр, стимулятор и околицентр не совпадают
- 2.7 Относительные высоты
- 7.1 Первое упражнение
- 7.2 Второе упражнение
- 7.3 Третье упражнение
Характеристики разносторонних треугольников
Масштабные треугольники являются простыми многоугольниками, потому что ни одна из их сторон или углов не имеет одинаковую меру, в отличие от равнобедренных и равносторонних треугольников..
Поскольку все его стороны и углы имеют разные измерения, эти треугольники считаются неправильными выпуклыми многоугольниками.
По амплитуде внутренних углов разносторонние треугольники классифицируются как:
- Шкала прямоугольник треугольник: все его стороны разные. Один из его углов прямой (90 или ) а остальные резкие и с разными мерами.
- Шкала тупого угла треугольника: все его стороны разные, и один из его углов тупой (> 90 или ).
- Шкала острого угла треугольника: все его стороны разные. Все его углы острые ( или ), с разными мерами.
Еще одной характеристикой разносторонних треугольников является то, что из-за несовместимости их сторон и углов они не имеют оси симметрии.
компоненты
Медиана: линия, которая выходит из средней точки одной стороны и достигает противоположной вершины. Три медианы совпадают в точке, называемой центроид или центроид.
Биссектриса: это луч, который делит каждый угол на два угла одинакового размера. Биссектрисы треугольника совпадают в точке, называемой incentro.
Посредник: это сегмент, перпендикулярный стороне треугольника, который начинается в середине этого. В треугольнике три медиатрицы, совпадающие в точке, называемой окружностью.
Высота: линия, идущая от вершины к противоположной стороне, а также эта линия перпендикулярна этой стороне. Все треугольники имеют три высоты, которые совпадают в точке, называемой ортоцентром.
свойства
Масштабные треугольники определены или идентифицированы, потому что они имеют несколько свойств, которые их представляют, возникших из теорем, предложенных великими математиками. Это:
Внутренние углы
Сумма внутренних углов всегда равна 180 или .
Сумма сторон
Сумма мер двух сторон всегда должна быть больше меры третьей стороны, a + b> c.
Непоследовательные стороны
Все стороны разносторонних треугольников имеют разные размеры или длины; то есть они неуместны.
Несогласованные углы
Поскольку все стороны разностороннего треугольника различны, их углы также будут разными. Однако сумма внутренних углов всегда будет равна 180º, и в некоторых случаях один из ее углов может быть тупым или прямым, в то время как в других все его углы будут острыми.
![]()
Высота, медиана, биссектриса и биссектриса не совпадают
Как и любой другой треугольник, в составной части есть несколько отрезков прямых линий, составляющих его, например: высота, медиана, биссектриса и биссектриса..
Из-за особенностей его сторон, в этом типе треугольника ни одна из этих линий не будет совпадать в одной.
Ортоцентр, барицентр, стимулятор и центр окружности не совпадают
Поскольку высота, медиана, биссектриса и биссектриса представлены различными отрезками прямых линий, в разностороннем треугольнике точки встречи - ортоцентр, центроцентр, стимулятор и окрицентр - будут находиться в разных точках (они не совпадают).
В зависимости от того, является ли треугольник острым, прямоугольным или разносторонним, ортоцентр имеет разные местоположения:
а. Если треугольник острый, ортоцентр будет внутри треугольника.
б. Если треугольник является прямоугольником, ортоцентр будет совпадать с вершиной прямой стороны.
с. Если треугольник тупой, ортоцентр будет находиться снаружи треугольника..
Относительные высоты
Высоты относительно сторон.
В случае разностороннего треугольника эти высоты будут иметь разные измерения. Каждый треугольник имеет три относительных высоты и для их расчета используется формула Герона.
Как рассчитать периметр?
Периметр многоугольника рассчитывается по сумме сторон.
Так как в этом случае разносторонний треугольник имеет все стороны с различной мерой, его периметр будет:
P = сторона a + сторона b + сторона c.
Как рассчитать площадь?
Площадь треугольников всегда рассчитывается по одной и той же формуле, умножая основание на высоту и деля на два:
Площадь = (база * ч) ÷ 2
В некоторых случаях высота разностороннего треугольника неизвестна, но есть математическая формула, предложенная математиком Хероном, для расчета площади, зная измерение трех сторон треугольника..
![]()
- a, b и c, представляют стороны треугольника.
- sp, соответствует полупериметру треугольника, то есть половине периметра:
В случае, если у вас есть измерение только двух сторон треугольника и угла, который сформирован между ними, площадь может быть рассчитана путем применения тригонометрических соотношений. Итак, вы должны:
Площадь = (сторона * ч) ÷ 2
Где высота (h) - произведение одной стороны на синус противоположного угла. Например, для каждой стороны площадь будет:
![]()
Как рассчитать высоту?
Поскольку все стороны разностороннего треугольника различны, вычислить высоту с помощью теоремы Пифагора невозможно.
Из формулы Герона, которая основана на измерениях трех сторон треугольника, можно вычислить площадь.
Высота может быть очищена от общей формулы площади:
![]()
Сторона заменяется измерением стороны a, b или c.
Другой способ вычислить высоту, когда известно значение одного из углов, состоит в применении тригонометрических соотношений, где высота будет представлять ногу треугольника..
Например, когда известен противоположный угол к высоте, он будет определяться синусом:
![]()
Как рассчитать стороны?
Если у вас есть мера двух сторон и угол, противоположный этим, можно определить третью сторону, применив теорему косинусов.
Например, в треугольнике AB показана высота относительно сегмента AC. Таким образом, треугольник делится на два прямоугольных треугольника.
![]()
Для вычисления c-стороны (отрезок AB) применяется теорема Пифагора для каждого треугольника:
Поскольку m = b - n, оно заменяется:
с 2 = ч 2 + б 2 (б - н) 2
с 2 = ч 2 + б 2 - 2 млрд + н 2 .
час 2 = а 2 - N 2
Он заменяется в предыдущем уравнении:
с 2 = а 2 - N 2 + б 2 - 2 млрд + н 2
с 2 = а 2 + б 2 - 2BN.
Зная, что п = а * cos C, заменяется в предыдущем уравнении, и получается значение стороны c:
с 2 = а 2 + б 2 - 2b* в * потому что C.
По закону косинусов стороны могут быть рассчитаны как:
- в 2 = б 2 + с 2 - 2b* с * потому что.
- б 2 = а 2 + с 2 - 2-й* с * потому что B.
- с 2 = а 2 + б 2 - 2b* в * потому что C.
Есть случаи, когда размеры сторон треугольника неизвестны, но их высота и углы, которые образуются в вершинах. Для определения площади в этих случаях необходимо применять тригонометрические соотношения.
Зная угол одной из его вершин, ноги идентифицируются и используется соответствующее тригонометрическое соотношение:
![]()
Например, катет AB будет противоположен углу C, но прилегает к углу A. В зависимости от стороны или катета, соответствующих высоте, другая сторона очищается, чтобы получить значение этого.
обучение
Первое упражнение
Рассчитайте площадь и высоту разностороннего треугольника ABC, зная, что его стороны:
![]()
решение
В качестве данных приведены измерения трех сторон разностороннего треугольника.
Поскольку у вас нет значения высоты, вы можете определить площадь, применяя формулу Герона..
Сначала рассчитывается полупериметр:
sp = (8 см + 12 см + 16 см) ÷ 2
Теперь значения в формуле Герона заменены:
![]()
Зная площадь, можно рассчитать относительную высоту на стороне b. Из общей формулы, очистив ее, вы получите:
Площадь = (сторона * ч) ÷ 2
46, 47 см 2 = (12 см * ч) ÷ 2
ч = (2 * 46,47 см 2 ) ÷ 12 см
h = 92,94 см 2 ÷ 12 см
Второе упражнение
Учитывая разносторонний треугольник ABC, меры которого:
В вершине B образуется угол 50 °. Рассчитайте относительную высоту в сторону с, периметр и площадь этого треугольника.
![]()
решение
В этом случае у вас есть меры двух сторон. Для определения высоты необходимо рассчитать измерение третьей стороны.
Поскольку задан угол, противоположный заданным сторонам, можно применить закон косинусов для определения измерения стороны переменного тока (b):
б 2 = а 2 + с 2 - 2-й*с * потому что B
б = переменный ток.
б 2 = (225) + (625) - (750) * 0,6427
б 2 = (225) + (625) - (482,025)
Поскольку у вас уже есть значение трех сторон, рассчитайте периметр этого треугольника:
P = сторона a + сторона b + сторона c
Р = 15 м + 25 м + 19, 18 м
Теперь можно определить площадь, применяя формулу Герона, но сначала необходимо рассчитать полупериметр:
Измерения сторон и полупериметра заменяются формулой Герона:
![]()
Наконец, зная площадь, можно рассчитать относительную высоту на стороне c. Из общей формулы, очистив ее, вы должны:
Площадь = (сторона * ч) ÷ 2
143,63 м 2 = (25 м * ч) ÷ 2
ч = (2 * 143,63 м 2 ) ÷ 25 м
h = 287,3 м 2 ÷ 25 м
Третье упражнение
В разностороннем треугольнике ABC сторона b имеет размер 40 см, сторона c имеет размер 22 см, а в вершине A образуется угол 90 или . Рассчитайте площадь этого треугольника.
![]()
решение
В этом случае даны измерения двух сторон разностороннего треугольника ABC, а также угла, образованного в вершине A.
Для определения площади нет необходимости вычислять меру стороны а, поскольку через тригонометрические соотношения угол используется для ее нахождения.
Так как угол, противоположный высоте, известен, это будет определяться произведением с одной стороны и синусом угла.
![]()
Мы отправляемся в путешествие по стране Геометрия, и первая наша остановка будет в городе Треугольников. Перед воротами города стоит необычный стражник. Чтобы пройти в город, нам нужно ответить на его вопросы. Вот они:
– Что такое треугольник?
Давайте ответим на вопрос стражника.
Треугольник – это замкнутая ломаная линия из 3-х звеньев. У треугольника 3 вершины, 3 угла и 3 стороны.
– Какие треугольники вы знаете? – спрашивает нас стражник.
![]()
Стражник удовлетворён нашими ответами и пропускает нас в город.
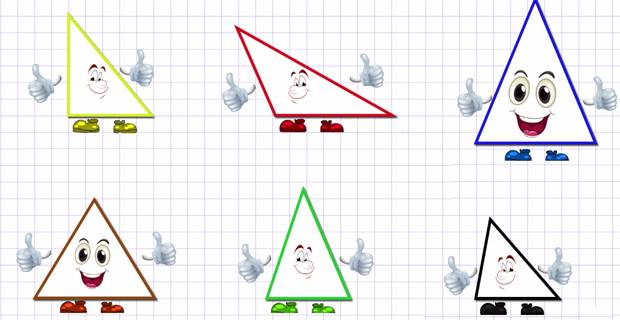
Что за чудо?! Все в этом городе треугольное. Дома – треугольные, окна и двери в домах – треугольные. На улицах растут треугольные деревья, а в садах на треугольных деревьях висят треугольные груши и яблоки. Треугольников в этом городе много, но какие они все разные: желтый – прямоугольный, красный – тупоугольный, остальные – остроугольные.
![]()
Давайте попробуем сами построить треугольники из палочек.
Перед нами палочки разной длины. У треугольника три стороны. Значит, нужно взять три палочки, вот только какие?
![]()
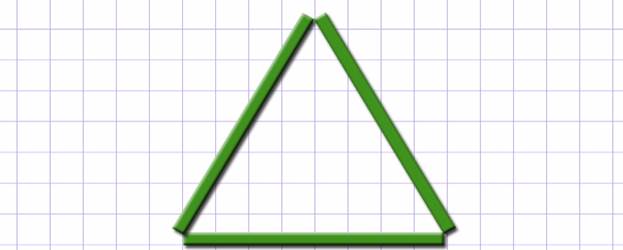
Давайте сначала возьмем три палочки одинаковой длины. Вот что у нас получилось.
![]()
У этого треугольника все стороны равны. Такой треугольник называется равносторонним треугольником.
Теперь возьмем 3 палочки так, чтобы две из них были одинаковой длины. Вот что у нас получилось.
![]()
Треугольник, у которого две стороны равны, называется равнобедренным. Кстати, равносторонний треугольник тоже можно назвать равнобедренным, так как у него любые две стороны одинаковой длины.
А если взять все три палочки разной длины, какой получится треугольник?
Возьмем коричневую, серую и малиновую палочки и попробуем построить треугольник. Что-то у нас ничего не получается, почему?
![]()
Оказывается, какие бы две стороны мы не взяли из трех, вместе они всегда должны быть длиннее третьей.
Треугольник, у которого все стороны разной длины, называется разносторонним.
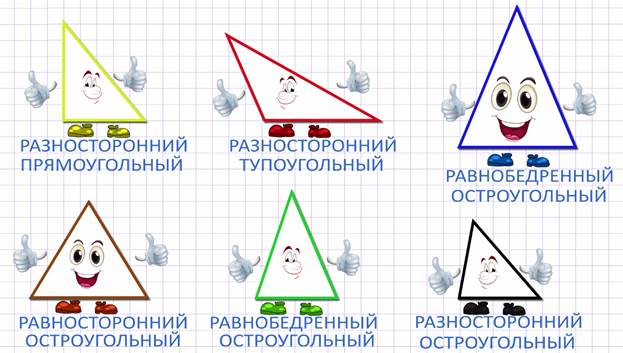
Таким образом, рассмотрев еще раз наших новых друзей, мы можем сказать, что коричневый треугольник будет называться равносторонним, зеленый и синий - равнобедренные треугольники, а красный, черный и желтый - разносторонние треугольники.
![]()
Получается, что треугольники могут быть разными и по углам, и по сторонам. Коричневый треугольник будет называться не только остроугольным, но и равносторонним, зеленый и синий – остроугольные и равнобедренные треугольники, красный – разносторонний и тупоугольный, желтый – также разносторонний, но прямоугольный, а черный – разносторонний и остроугольный треугольник.
Читайте также: